Лекция 21 Тема 6 АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ

Лекция 21 Тема № 6 АЛГОРИТМИЗАЦИЯ И ПРОГРАММИРОВАНИЕ Понятие алгоритма и его свойства. Способы описания алгоритмов. Основные алгоритмические конструкции.

6. 1 Понятие алгоритма и его свойства. Происхождение термина алгоритм – математик Аль-Хорезми в 825 г. описал правила выполнения четырех арифметических действий в десятичной системе счисления. Процесс их выполнения был назван алгоризмом алгорисмус алгорифм алгоритм. Первоначально под алгоритмом понимали способ выполнения арифметических действий над десятичными числами. В дальнейшем это понятие стали использовать для обозначения любой последовательности действий, приводящей к решению поставленной задачи. Алгоритм — это формальное описание способа решения задачи путем разбиения ее на конечную по времени последовательность действий (элементарных операций). Алгоритм — описанная на некотором языке точная конечная система правил, определяющая содержание и порядок действий над некоторыми объектами, строгое выполнение которых дает решение поставленной задачи.

Алгоритм (по Колмогорову) — это система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи. Алгоритм (по Маркову) — это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату Пусть DZ – область (множество) исходных данных задачи Z, а R – множество возможных результатов, тогда алгоритм осуществляет отображение DZ R. Алгоритм называется частичным, если мы получаем результат только для некоторых значений d, принадлежащих DZ. Алгоритм называется полным если получает правильный результат для всех значений d, принадлежащих DZ. Алгоритмы можно разделить на численные и логические. Численные алгоритмы – это алгоритмы, в соответствии с которыми решение задач сводится к арифметическим действиям. Логические алгоритмы - это алгоритмы , в соответствии с которыми решение задач сводится к логическим действиям.

Любой алгоритм существует не сам по себе, а предназначен для определенного исполнителя (человека, робота, компьютера, языка программирования и т. д. ). Совокупность команд, которые данный исполнитель умеет выполнять, называется системой команд исполнителя. Алгоритм описывается в командах исполнителя, который будет его реализовывать. Объекты, над которыми исполнитель может совершать действия, образуют так называемую среду исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм. Алгоритм характеризуется следующими свойствами: qдискретностью, qмассовостью, qопределенностью, qрезультативностью, qформальностью.

Дискретность (разрывность — противоположно непрерывности)— это свойство алгоритма, характеризующее его структуру: каждый алгоритм состоит из отдельных законченных действий, говорят: «Делится на шаги» . Массовость — применимость алгоритма ко всем задачам рассматриваемого типа, при любых исходных данных. Определенность (детерминированность, точность) — свойство алгоритма, указывающее на то, что каждый шаг алгоритма должен быть строго определен и не допускать различных толкований; также строго должен быть определен порядок выполнения отдельных шагов. Результативность — свойство, состоящее в том, что любой алгоритм должен завершаться за конечное (может быть очень большое) число шагов. Формальность - это свойство указывает на то, что любой исполнитель, способный воспринимать и выполнять инструкции алгоритма, действует формально, т. е. отвлекается от содержания поставленной задачи и лишь строго выполняет инструкции.

Формализация понятия алгоритма посредством машины Поста Машина Поста представляет собой абстрактный механизм для выполнения алгоритмов, который состоит из двух узлов • бесконечной ленты разделенной на ячейки, каждая из которых может быть помечена или не помечена меткой V; • механизма чтения-записи (в дальнейшем — каретка), который может перемещаться вдоль ленты вправо и влево, записывать метку в пустую ячейку, стирать метку в помеченной ячейке и проверять наличие метки в ячейке. Инструкции машины Поста Пометить ячейку, если она пуста, и перейти к инструкции j Стереть метку, если она есть, и перейти к инструкции j Переместиться влево на 1 ячейку и перейти к инструкции j Переместиться вправо на 1 ячейку и перейти к инструкции j Определить, помечена ячейка или нет. Если ячейка пуста, перейти на инструкцию ju если помечена — на инструкцию j 2 Остановиться

Формализация понятия алгоритма посредством машины Тьюринга «Конструктивно» машина Тьюринга, так же как и машина Поста, состоит из двух основных узлов: ленты с ячейками и каретки. Решаемая проблема задается путем записи на ленту конечного количества символов, образующих слово в алфавите где е — это специальный пустой символ, показывающий отсутствие любого символа алфавита S в ячейке. е S 1 S 2 S 3 S 4 Sn е В отличие от машины Поста, в машине Тьюринга каретка неподвижна, а лента проматывается лентопротяжным механизмом на одну ячейку вправо или влево. Управляется машина при помощи функции переходов, которая называется программой машины Тьюринга и может быть задана в виде таблицы или орграфа. При этом при задании функции переходов используются как команды лентопротяжному механизму (смещение ленты на одну ячейку вправо, смещение ленты на одну ячейку влево, перемотка в начало, останов), так и команды каретки (запись нового символа, чтение символа, запись пустого символа).

6. 2 Способы описания алгоритмов. Способы описания алгоритма: Словесное описание Псевдокод Блок-схема Программа Словесное описание представляет структуру алгоритма на естественном языке. Этот способ описания строго не формализуем (под «формализуемостью» понимается то, что описание абсолютно полное и учитывает все возможные ситуации, которые могут возникнуть в ходе решения); допускает неоднозначность толкования при описании некоторых действий; страдает многословностью. 1. Начало алгоритма. 2. Выполнить некоторое действие (оператор) s 1. 3. Если выполнено условие «Усл 1» , то выполнить операторы s 2, s 3 и перейти к п. 4. Иначе – перейти к п. 3. 1. Пока выполняется «Усл 2» выполнить п. 3. 2 и п. 3. 3, далее перейти к п. 4. 3. 2. … 1. Выполнить оператор s 8. 2. Конец алгоритма.

Псевдокод — описание структуры алгоритма на естественном, частично формализованном языке, позволяющее выявить основные этапы решения задачи, перед точной его записью на языке программирования. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Блок-схема — описание структуры алгоритма с помощью геометрических фигур с линиями-связями, показывающими порядок выполнения отдельных инструкций (ГОСТ 19. 701 -90, ИСО 5807 -85). В блок-схеме каждой формальной конструкции соответствует определенная геометрическая фигура или связанная линиями совокупность фигур. Разновидности визуального формализма: Запись алгоритма с использованием диаграмм Нэсси. Шнейдермана. Запись алгоритма с использованием P-схемы.

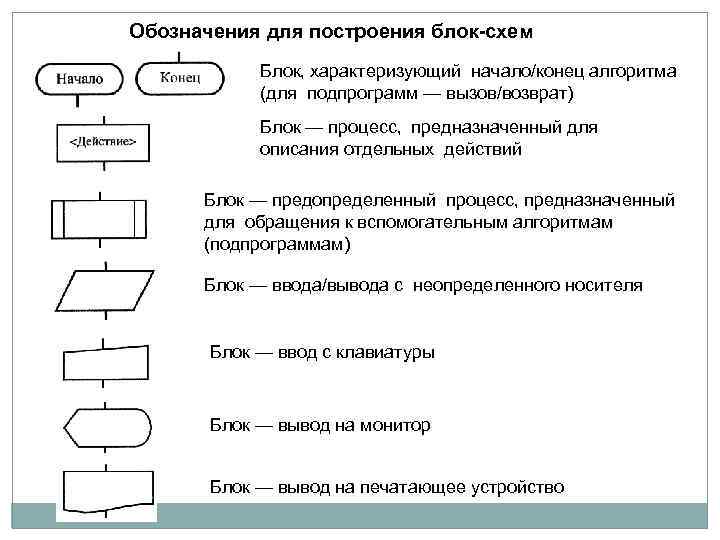Обозначения для построения блок-схем Блок, характеризующий начало/конец алгоритма (для подпрограмм — вызов/возврат) Блок — процесс, предназначенный для описания отдельных действий Блок — предопределенный процесс, предназначенный для обращения к вспомогательным алгоритмам (подпрограммам) Блок — ввода/вывода с неопределенного носителя Блок — ввод с клавиатуры Блок — вывод на монитор Блок — вывод на печатающее устройство

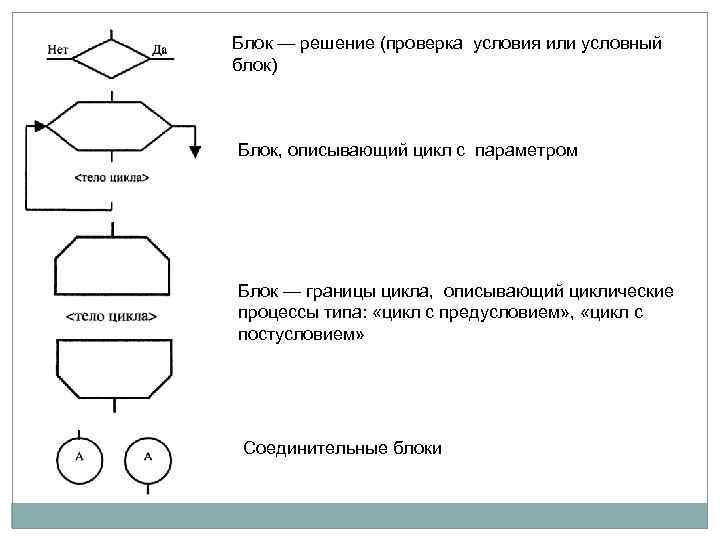Блок — решение (проверка условия или условный блок) Блок, описывающий цикл с параметром Блок — границы цикла, описывающий циклические процессы типа: «цикл с предусловием» , «цикл с постусловием» Соединительные блоки

6. 3 Основные алгоритмические конструкции. линейные (последовательные), разветвляющиеся, циклические, рекурсивные.

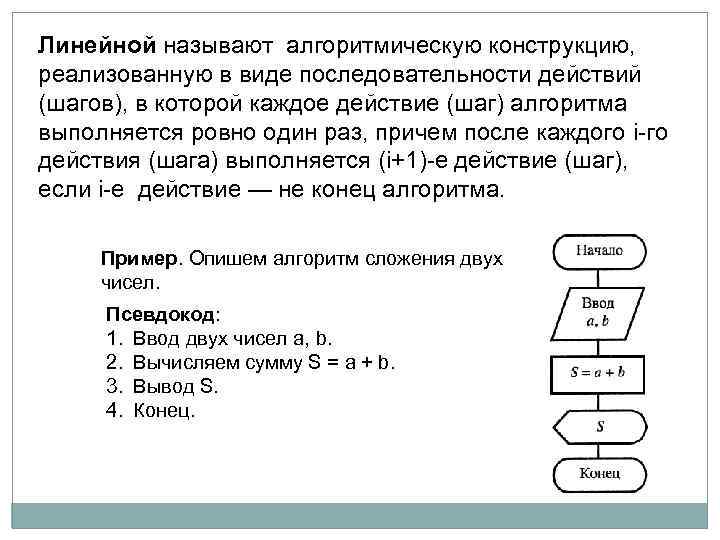Линейной называют алгоритмическую конструкцию, реализованную в виде последовательности действий (шагов), в которой каждое действие (шаг) алгоритма выполняется ровно один раз, причем после каждого i-го действия (шага) выполняется (i+1)-е действие (шаг), если i-е действие — не конец алгоритма. Пример. Опишем алгоритм сложения двух чисел. Псевдокод: 1. Ввод двух чисел a, b. 2. Вычисляем сумму S = а + b. 3. Вывод S. 4. Конец.

Разветвляющейся (или ветвящейся) называется алгоритмическая конструкция, обеспечивающая выбор между двумя альтернативами в зависимости от значения входных данных. При каждом конкретном наборе входных данных разветвляющийся алгоритм сводится к линейному. Различают неполное (если — то) и полное (если — то — иначе) ветвления. Полное ветвление позволяет организовать две ветви в алгоритме (то или иначе), каждая из которых ведет к общей точке их слияния, так что выполнение алгоритма продолжается независимо от того, какой путь был выбран. Неполное ветвление предполагает наличие некоторых действий алгоритма только на одной ветви (то), вторая ветвь отсутствует, т. е. для одного из результатов проверки никаких действий выполнять не надо, управление сразу переходит к точке слияния

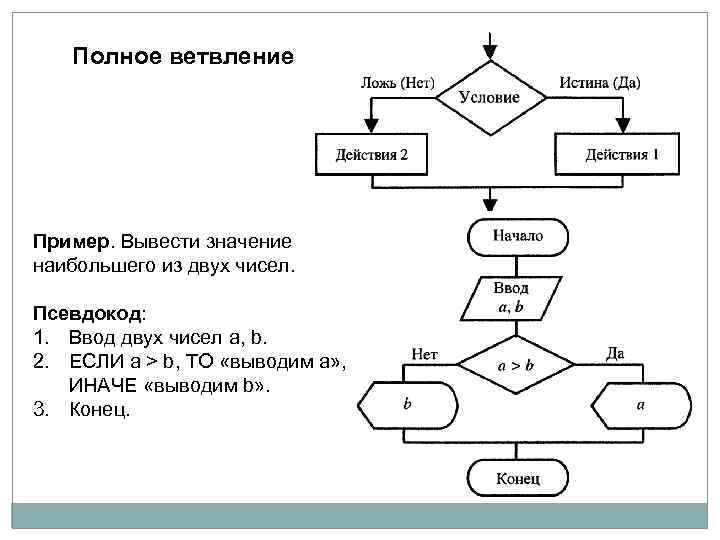Полное ветвление Пример. Вывести значение наибольшего из двух чисел. Псевдокод: 1. Ввод двух чисел a, b. 2. ЕСЛИ a > b, ТО «выводим а» , ИНАЧЕ «выводим b» . 3. Конец.

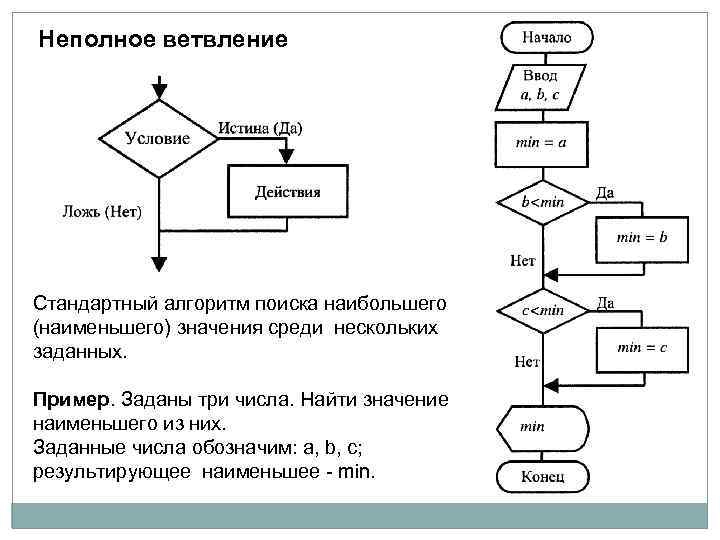Неполное ветвление Стандартный алгоритм поиска наибольшего (наименьшего) значения среди нескольких заданных. Пример. Заданы три числа. Найти значение наименьшего из них. Заданные числа обозначим: а, b, с; результирующее наименьшее - min.

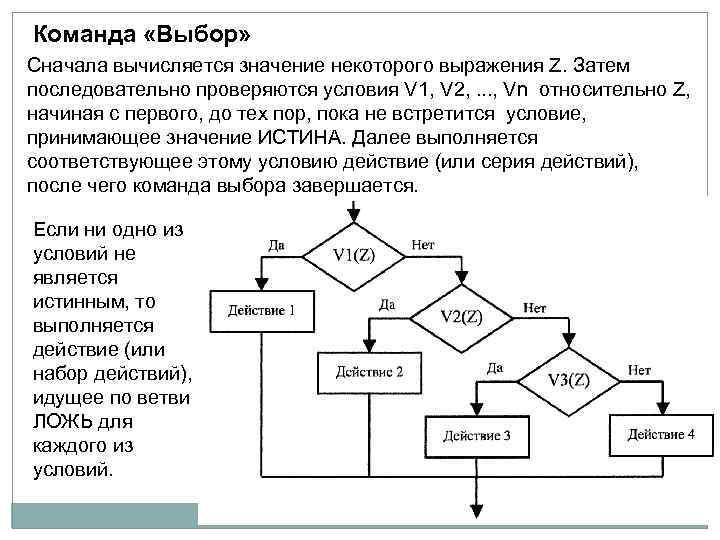Команда «Выбор» Сначала вычисляется значение некоторого выражения Z. Затем последовательно проверяются условия V 1, V 2, . . . , Vn относительно Z, начиная с первого, до тех пор, пока не встретится условие, принимающее значение ИСТИНА. Далее выполняется соответствующее этому условию действие (или серия действий), после чего команда выбора завершается. Если ни одно из условий не является истинным, то выполняется действие (или набор действий), идущее по ветви ЛОЖЬ для каждого из условий.

Циклической (или циклом) называют алгоритмическую конструкцию, в которой некая, идущая подряд группа действий (шагов) алгоритма может выполняться несколько раз, в зависимости от входных данных или условия задачи. Группа повторяющихся действий на каждом шагу цикла называется телом цикла. Цикл с параметром (арифметический цикл) Цикл с предусловием В арифметическом цикле число его шагов (повторений) однозначно определяется правилом изменения параметра, которое задается с помощью начального (N) и конечного (К) значений параметра и шагом (h) его изменения. На последнем шаге цикла значение параметра не больше К, но такое, что дальнейшее его изменение приведет к значению, большему, чем К. Цикл с постусловием

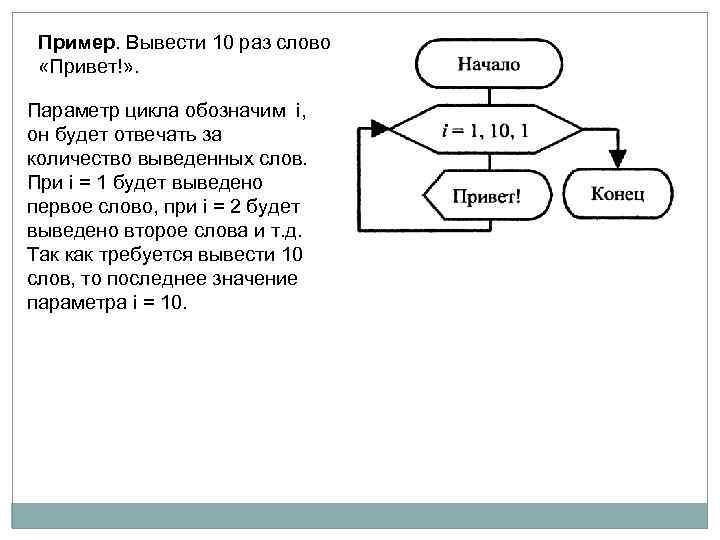Пример. Вывести 10 раз слово «Привет!» . Параметр цикла обозначим i, он будет отвечать за количество выведенных слов. При i = 1 будет выведено первое слово, при i = 2 будет выведено второе слова и т. д. Так как требуется вывести 10 слов, то последнее значение параметра i = 10.

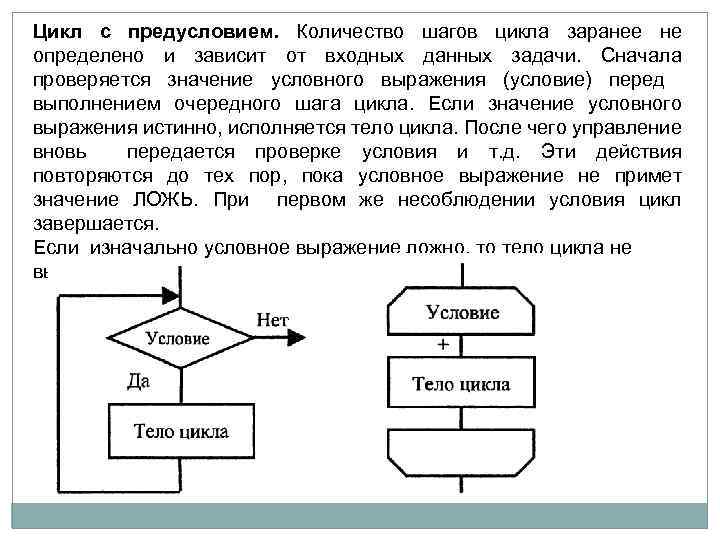Цикл с предусловием. Количество шагов цикла заранее не определено и зависит от входных данных задачи. Сначала проверяется значение условного выражения (условие) перед выполнением очередного шага цикла. Если значение условного выражения истинно, исполняется тело цикла. После чего управление вновь передается проверке условия и т. д. Эти действия повторяются до тех пор, пока условное выражение не примет значение ЛОЖЬ. При первом же несоблюдении условия цикл завершается. Если изначально условное выражение ложно, то тело цикла не выполнится ни разу.

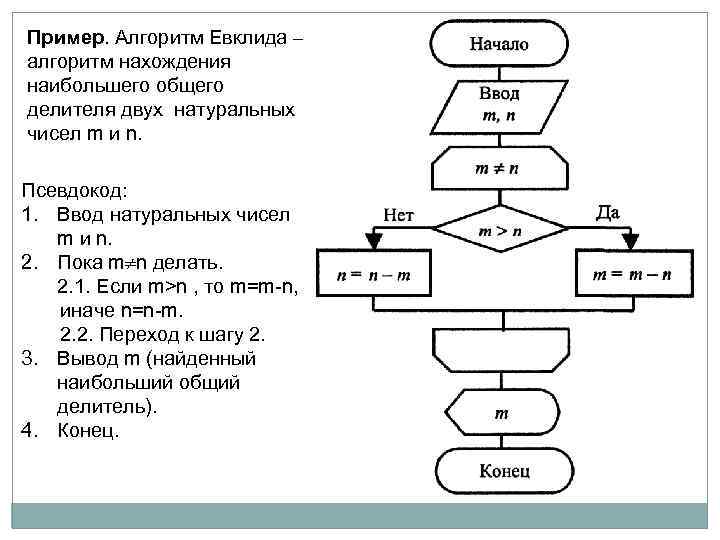Пример. Алгоритм Евклида — алгоритм нахождения наибольшего общего делителя двух натуральных чисел m и n. Псевдокод: 1. Ввод натуральных чисел m и n. 2. Пока m n делать. 2. 1. Если m>n , то m=m-n, иначе n=n-m. 2. 2. Переход к шагу 2. 3. Вывод m (найденный наибольший общий делитель). 4. Конец.

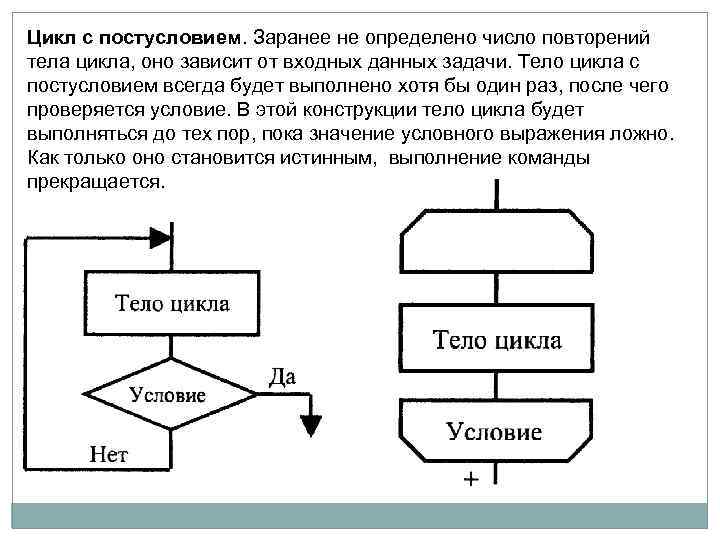Цикл с постусловием. Заранее не определено число повторений тела цикла, оно зависит от входных данных задачи. Тело цикла с постусловием всегда будет выполнено хотя бы один раз, после чего проверяется условие. В этой конструкции тело цикла будет выполняться до тех пор, пока значение условного выражения ложно. Как только оно становится истинным, выполнение команды прекращается.

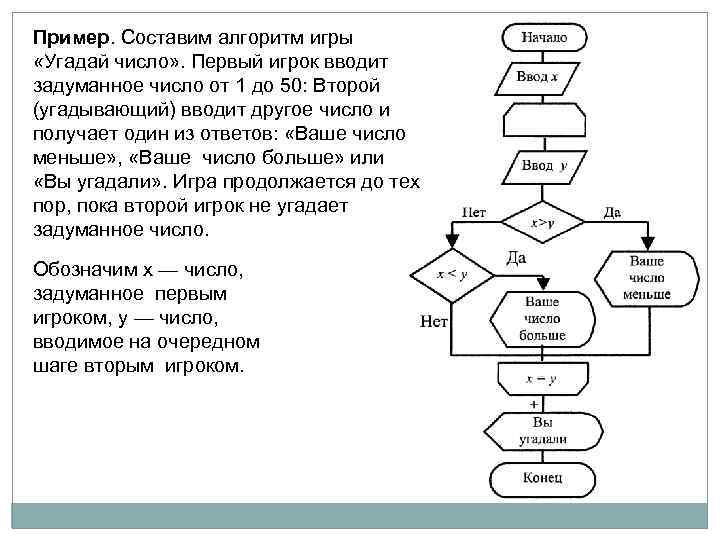Пример. Составим алгоритм игры «Угадай число» . Первый игрок вводит задуманное число от 1 до 50: Второй (угадывающий) вводит другое число и получает один из ответов: «Ваше число меньше» , «Ваше число больше» или «Вы угадали» . Игра продолжается до тех пор, пока второй игрок не угадает задуманное число. Обозначим х — число, задуманное первым игроком, у — число, вводимое на очередном шаге вторым игроком.

Расположение циклов последовательные вложенные запрещенные Алгоритм любой задачи может быть представлен как комбинация представленных выше элементарных алгоритмических структур, поэтому данные конструкции: линейную, ветвящуюся и циклическую, называют базовыми. Рекурсивный алгоритм. Рекурсивным называется алгоритм, организованный таким образом, что в процессе выполнения команд на каком-либо шаге он прямо или косвенно обращается сам к себе.

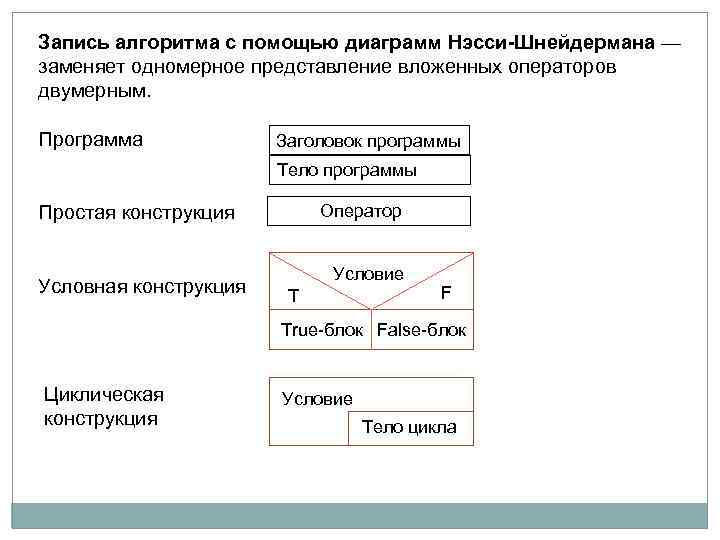Запись алгоритма с помощью диаграмм Нэсси-Шнейдермана — заменяет одномерное представление вложенных операторов двумерным. Программа Заголовок программы Тело программы Оператор Простая конструкция Условная конструкция Условие T F True-блок False-блок Циклическая конструкция Условие Тело цикла

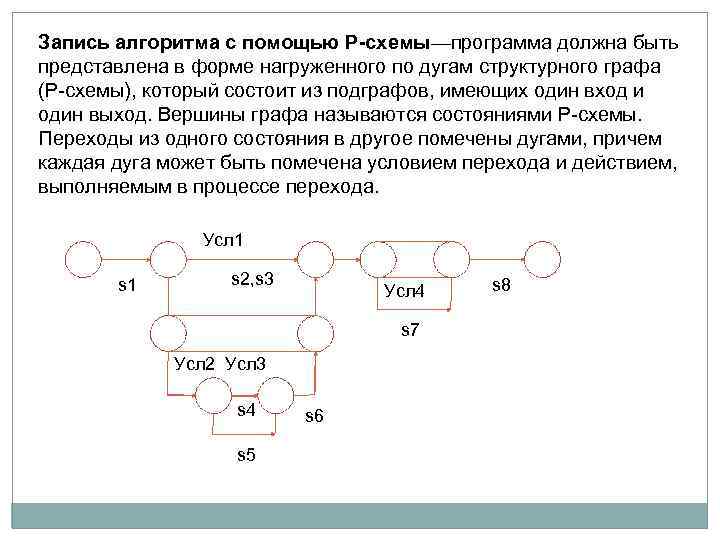Запись алгоритма с помощью P-схемы—программа должна быть представлена в форме нагруженного по дугам структурного графа (Р-схемы), который состоит из подграфов, имеющих один вход и один выход. Вершины графа называются состояниями Р-схемы. Переходы из одного состояния в другое помечены дугами, причем каждая дуга может быть помечена условием перехода и действием, выполняемым в процессе перехода. Усл 1 s 2, s 3 Усл 4 s 7 Усл 2 Усл 3 s 4 s 5 s 6 s 8

Программы – это алгоритмы и структуры данных. Формула Никлауса Вирта: Алгоритмы + структуры данных = Программы Структуры данных представляют исходные данные, промежуточные и конечные результаты. Алгоритмы – указания о том, какие действия и в какой последовательности необходимо применять к данным для получения требуемого конечного результата Все данные, обрабатываемые компьютером, хранятся в ячейках памяти компьютера, каждая из которых имеет свой адрес. Для того чтобы не следить за тем, по какому адресу будут записаны те или иные данные, в языках программирования используется понятие переменной, позволяющее отвлечься от адреса ячейки памяти и обращаться к ней с помощью имени (идентификатора).

Переменные и константы Переменная — есть именованный объект (ячейка памяти), который может изменять свое значение. Тип переменной задает: § используемый способ записи информации в ячейки памяти; § необходимый объем памяти для ее хранения. Если переменные присутствуют в программе, на протяжении всего времени ее работы — их называют статическими. Переменные, создающиеся и уничтожающиеся на разных этапах выполнения программы, называют динамическими. Все остальные данные в программе, значения которых не изменяется на протяжении работы программы называются константами или постоянными. Константы, как и переменные имеют тип.

Типы данных • Простые o Целочисленные o Символьные (литерные) o Логические o Вещественные o Указательные • Структурированные o Массивы o Классы • Для порядковых типов пользователь может создавать перечислимые и интервальные типы Тип-диапазон Перечисляемые o Множества o Файлы • Простые типы, кроме вещественного, являются порядковыми o Записи o Строки • Простые типы называют базовыми. o Процедурные o Вариантные

Структурные типы данных Тип данных, позволяющий хранить вместе под одним именем несколько переменных, называется структурированным. Служат для описания данных, которые могут содержать много значений, а не только одно как данные простых типов. При использовании переменной структурированного типа память отводится сразу под несколько значений простого или структурированного типа данных.

Классификация структурированных типов данных Однородные, у которых все элементы одинакового типа (массивы, строки, множества, файлы) Неоднородные (комбинированные), которые объединяют в единое целое разнотипные элементы (записи, экземпляры классов (объекты))

Массив - упорядоченная индексированная совокупность однотипных элементов, имеющих общее имя. Массив определяется: именем (идентификатором), который является единым для всех элементов массива; количеством размерностей (координат), необходимых для указания местонахождения требуемого элемента (одномерных, двумерных и других массивов). Особенности массивов • все элементы имеют один тип • • весь массив имеет одно имя все элементы расположены в памяти рядом

Конфигурация массивов Определяется размерностью массива: одномерный многомерный В одномерном (линейном) массиве для указания месторасположения его элементов используется только один индекс. В многомерном массиве для указания месторасположения его элементов используются несколько индексов.

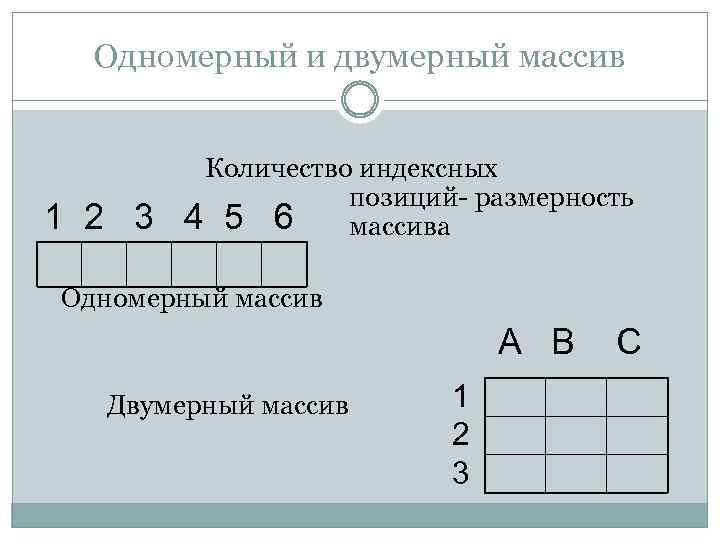Одномерный и двумерный массив 1 2 3 Количество индексных позиций- размерность 4 5 6 массива Одномерный массив A B Двумерный массив 1 2 3 C

Массивы A НОМЕР массив 1 2 5 10 A[1] A[2] 3 3 15 15 элемента массива (ИНДЕКС) 4 5 20 25 A[3] ЗНАЧЕНИЕA[4] A[5] элемента массива НОМЕР (ИНДЕКС) элемента массива: 2 A[2] ЗНАЧЕНИЕ элемента массива: 10

В качестве индексов могут использоваться константы или переменные порядковых типов данных. Тип индексов и их количество (размерность массива) определяются при описании массива. Статические массивы - размер фиксирован и определён до начала программы Динамические массивы - размер можно задать в ходе выполнения программы

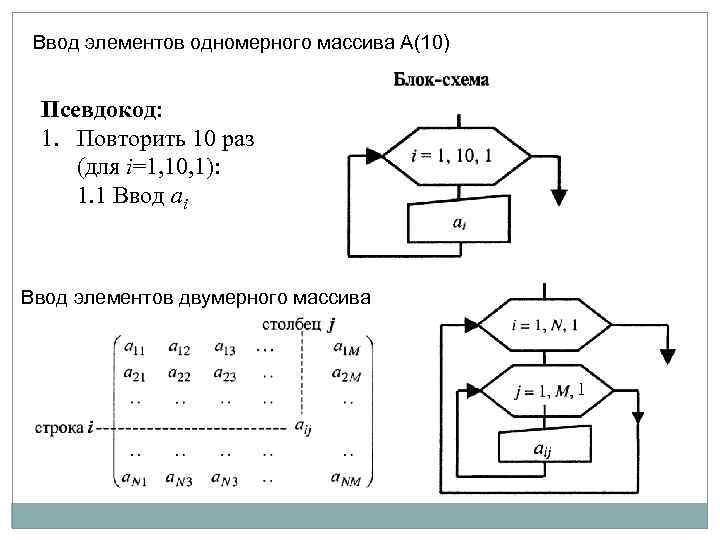Ввод элементов одномерного массива А(10) Псевдокод: 1. Повторить 10 раз (для i=1, 10, 1): 1. 1 Ввод ai Ввод элементов двумерного массива 1