Скачать презентацию Лекция 21 Спектральный метод анализа электрических цепей Скачать презентацию Лекция 21 Спектральный метод анализа электрических цепей

электротехника 18.ppt

  • Количество слайдов: 43

Лекция № 21 Спектральный метод анализа электрических цепей Лекция № 21 Спектральный метод анализа электрических цепей

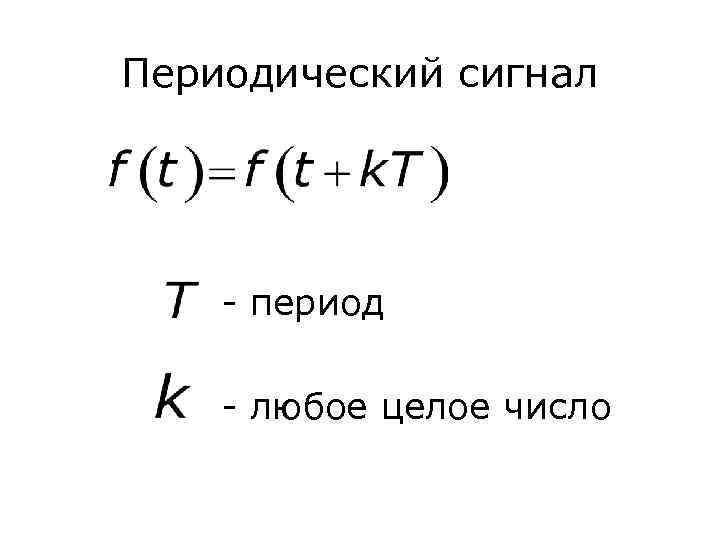Периодический сигнал - период - любое целое число Периодический сигнал - период - любое целое число

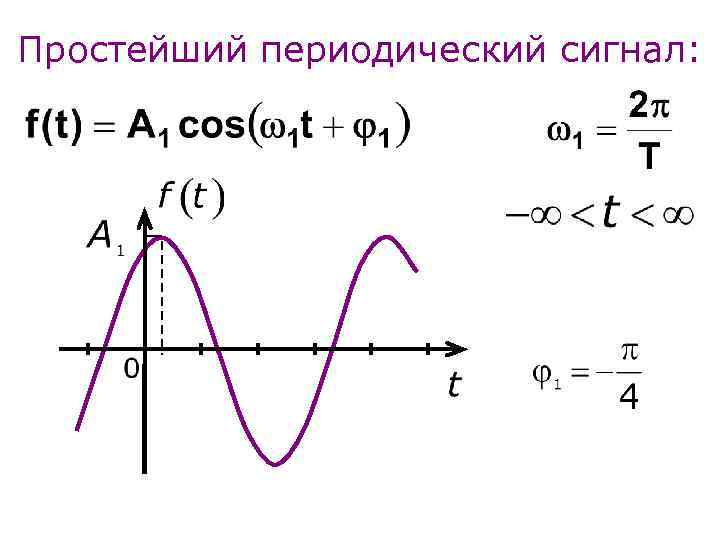Простейший периодический сигнал: Простейший периодический сигнал:

Совокупность амплитуд - спектр амплитуд Совокупность начальных фаз - спектр фаз Совокупность амплитуд - спектр амплитуд Совокупность начальных фаз - спектр фаз

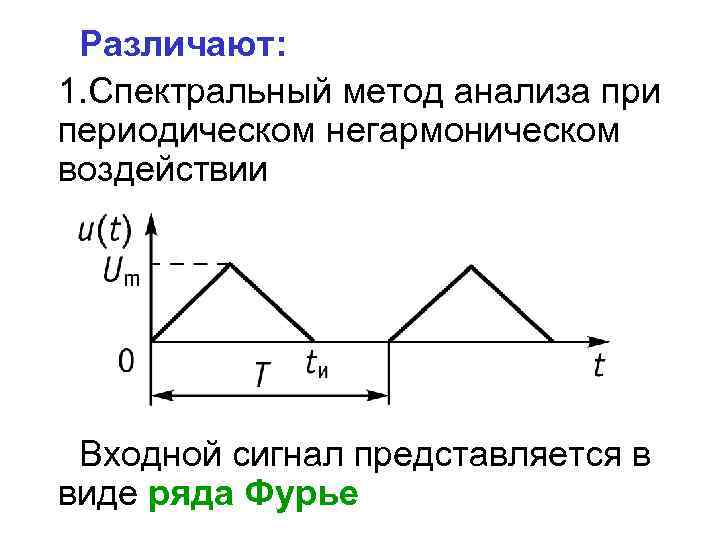Различают: 1. Спектральный метод анализа при периодическом негармоническом воздействии Входной сигнал представляется в виде Различают: 1. Спектральный метод анализа при периодическом негармоническом воздействии Входной сигнал представляется в виде ряда Фурье

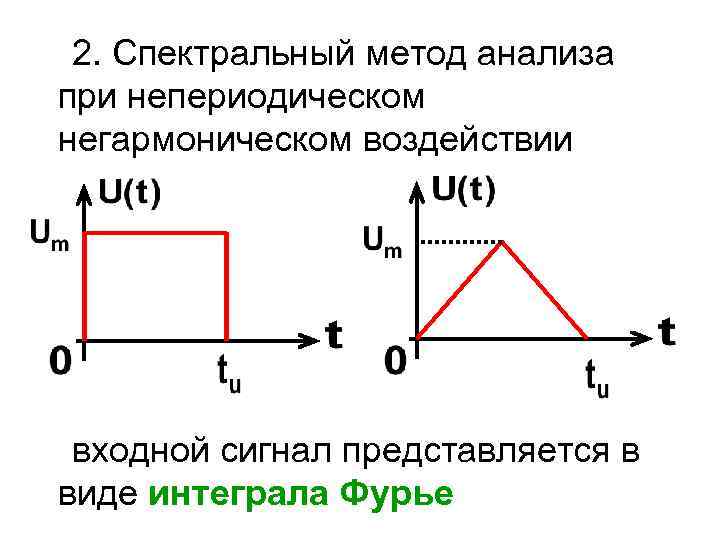2. Спектральный метод анализа при непериодическом негармоническом воздействии входной сигнал представляется в виде интеграла 2. Спектральный метод анализа при непериодическом негармоническом воздействии входной сигнал представляется в виде интеграла Фурье

Спектры периодических сигналов Спектры периодических сигналов

Периодические несинусоидальные токи и напряжения возникают в цепи при следующих режимах работы: 1. Источник Периодические несинусоидальные токи и напряжения возникают в цепи при следующих режимах работы: 1. Источник несинусоидальный, все элементы цепи (R, L, C) линейные. 2. Источник синусоидальный, один или несколько элементов цепи нелинейные. 3. Источник постоянный или синусоидальный, один или несколько элементов цепи периодически изменяются во времени

Если функция удовлетворяет условиям Дирихле: 1. Имеет на периоде конечное число разрывов первого рода Если функция удовлетворяет условиям Дирихле: 1. Имеет на периоде конечное число разрывов первого рода 2. Имеет на периоде конечное число максимумов и минимумов То она может быть разложена в ряд Фурье

1. Тригонометрическая форма ряда Фурье 1. Тригонометрическая форма ряда Фурье

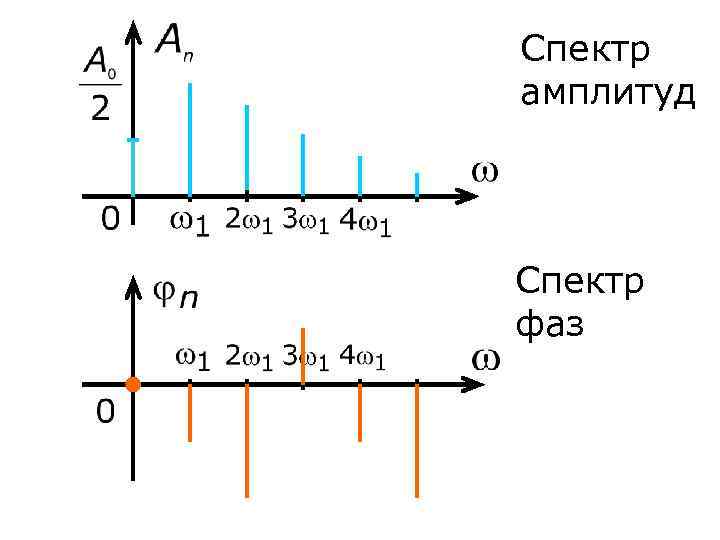Спектр амплитуд Спектр фаз Спектр амплитуд Спектр фаз

2. Комплексная форма ряда Фурье 2. Комплексная форма ряда Фурье

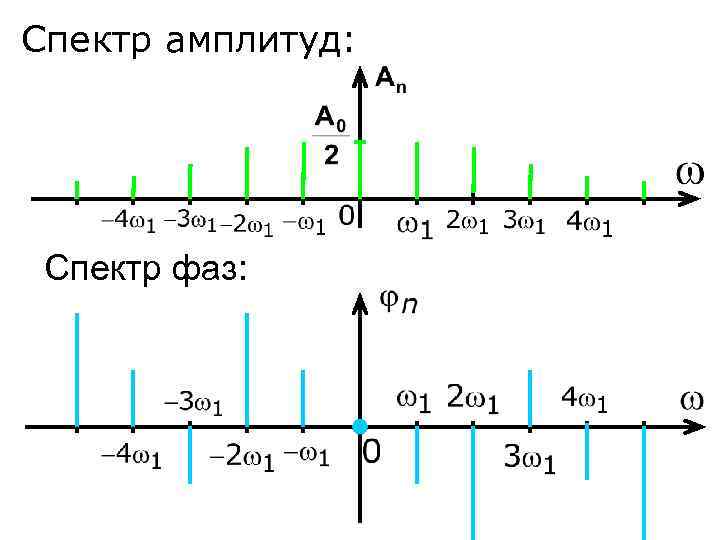Спектр амплитуд: Спектр фаз: Спектр амплитуд: Спектр фаз:

Вывод: 1. Спектр периодического сигнала является дискретным 2. Расстояния между спектральными линиями - период Вывод: 1. Спектр периодического сигнала является дискретным 2. Расстояния между спектральными линиями - период сигнала

3. Чем больше период повторения, тем чаще располагаются спектральные составляющие 3. Чем больше период повторения, тем чаще располагаются спектральные составляющие

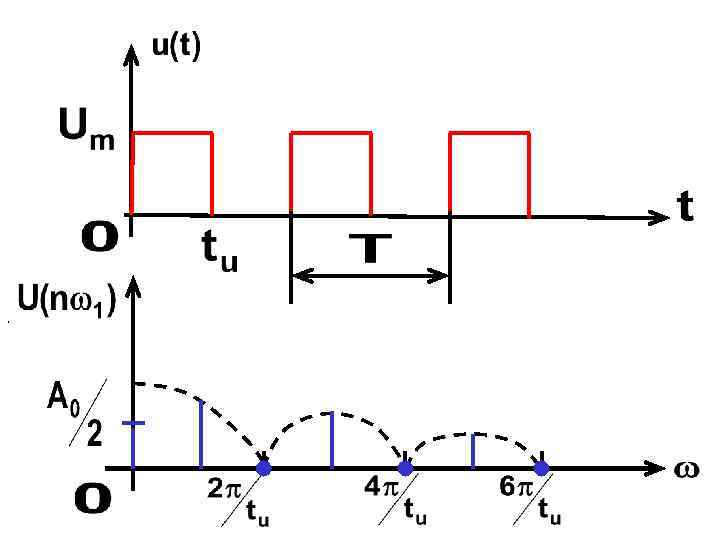
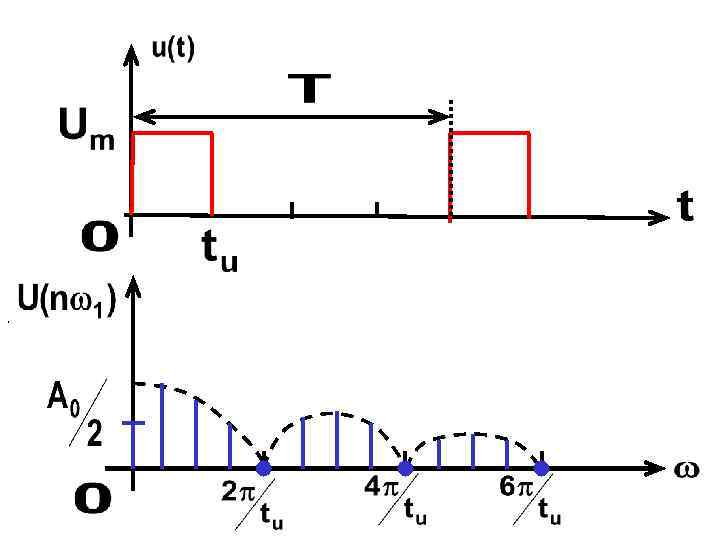
Спектр периодической последовательности прямоугольных импульсов Спектр периодической последовательности прямоугольных импульсов

- длительность импульса - амплитуда - скважность - длительность импульса - амплитуда - скважность

Нули: Частоты, на которых амплитуды равны нулю: Нули: Частоты, на которых амплитуды равны нулю:

Номера гармоник, амплитуды которых равны нулю: Номера гармоник, амплитуды которых равны нулю:

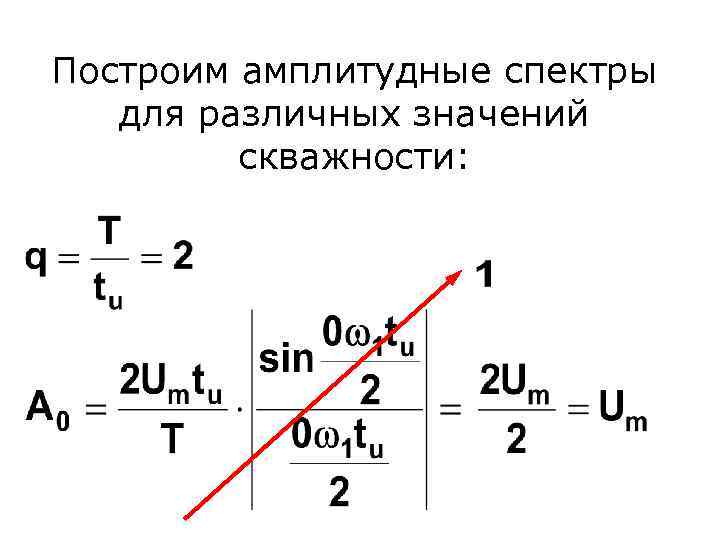Построим амплитудные спектры для различных значений скважности: Построим амплитудные спектры для различных значений скважности:

, ,

, ,

Выводы: 1. Огибающая амплитудного спектра изменяется по закону функции 2. Огибающая имеет нули на Выводы: 1. Огибающая амплитудного спектра изменяется по закону функции 2. Огибающая имеет нули на частотах

3. Спектр дискретный. Расстояние по частоте между гармоническими составляющими равно 4. Количество составляющих между 3. Спектр дискретный. Расстояние по частоте между гармоническими составляющими равно 4. Количество составляющих между нулями равно

5. При и увеличении (уменьшении) расстояние между гармоническими составляющими остается постоянным, а расстояние между 5. При и увеличении (уменьшении) расстояние между гармоническими составляющими остается постоянным, а расстояние между нулями огибающей уменьшается (увеличивается)

6. При и увеличении (уменьшении) периода T расстояние между нулями огибающей остается постоянным, а 6. При и увеличении (уменьшении) периода T расстояние между нулями огибающей остается постоянным, а расстояние между составляющими уменьшается (увеличивается)