 Лекция № 21 -22: «Дифракционная решетка»
Лекция № 21 -22: «Дифракционная решетка»
 Вопросы: ØМноголучевая интерференция от дифракционной решетки; ØУстройство дифракционной решетки; ØСпектральные характеристики решеток; ØДифракция рентгеновских лучей; ØФормула Вульфа-Бреггов; ØПонятие о рентгеноструктурном анализе;
Вопросы: ØМноголучевая интерференция от дифракционной решетки; ØУстройство дифракционной решетки; ØСпектральные характеристики решеток; ØДифракция рентгеновских лучей; ØФормула Вульфа-Бреггов; ØПонятие о рентгеноструктурном анализе;
 Интерференция от дифракционной решетки. Назначение: Дифракционная решетка является важнейшим спектральным прибором, предназначенным для разложения сложного (белого) света в спектр, измерения длин волн и исследования отдельных спектральных компонентов (линий). Устройство: дифракционная решетка представляет собой стеклянную(или металлическую) пластинку, на которую с помощью специальной делительной машины нанесено большое число (например: 600 штр. /мм, 1200 штр. /мм и др. ) равноотстоящих штрихов одинаковой конфигурации (например: прямых параллельных другу. ) Эти штрихи выполняют роль непрозрачных преград, а промежутки между штрихами- роль щелей. Рассмотрим простейшую идеализированную решетку, состоящую из одинаковых равноотстоящих щелей в непрозрачном экране. Пусть ширина каждой щели равна B, а период решетки (то есть расстояние между соответствующими краями соседних щелей или сумма (B+A), где А-ширина непрозрачного участка) есть D. Следует отметить, что от дифракционной решетки реализуется многолучевая интерференция когерентных дифрагированных пучков света, исходящих из N щелей решетки при ее освещении.
Интерференция от дифракционной решетки. Назначение: Дифракционная решетка является важнейшим спектральным прибором, предназначенным для разложения сложного (белого) света в спектр, измерения длин волн и исследования отдельных спектральных компонентов (линий). Устройство: дифракционная решетка представляет собой стеклянную(или металлическую) пластинку, на которую с помощью специальной делительной машины нанесено большое число (например: 600 штр. /мм, 1200 штр. /мм и др. ) равноотстоящих штрихов одинаковой конфигурации (например: прямых параллельных другу. ) Эти штрихи выполняют роль непрозрачных преград, а промежутки между штрихами- роль щелей. Рассмотрим простейшую идеализированную решетку, состоящую из одинаковых равноотстоящих щелей в непрозрачном экране. Пусть ширина каждой щели равна B, а период решетки (то есть расстояние между соответствующими краями соседних щелей или сумма (B+A), где А-ширина непрозрачного участка) есть D. Следует отметить, что от дифракционной решетки реализуется многолучевая интерференция когерентных дифрагированных пучков света, исходящих из N щелей решетки при ее освещении.
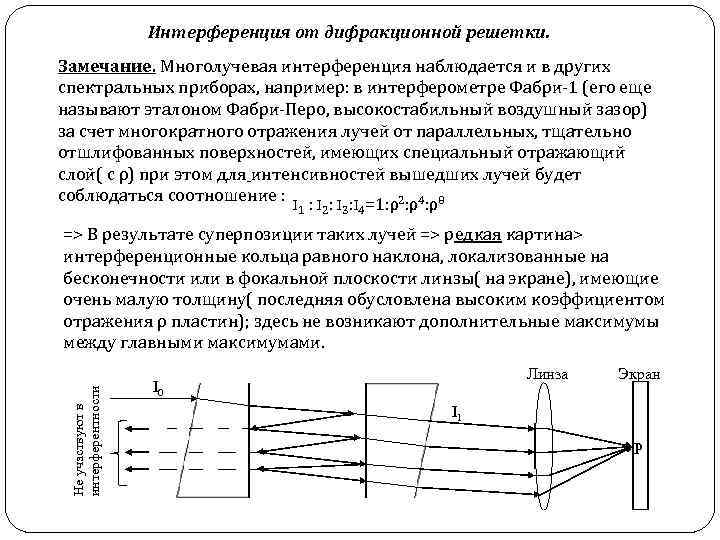 Интерференция от дифракционной решетки. Замечание. Многолучевая интерференция наблюдается и в других спектральных приборах, например: в интерферометре Фабри-1 (его еще называют эталоном Фабри-Перо, высокостабильный воздушный зазор) за счет многократного отражения лучей от параллельных, тщательно отшлифованных поверхностей, имеющих специальный отражающий слой( с ρ) при этом для интенсивностей вышедших лучей будет соблюдаться соотношение : I : I =1: ρ2: ρ4: ρ8 1 2 3 4 Не участвуют в интерферентности => В результате суперпозиции таких лучей => редкая картина> интерференционные кольца равного наклона, локализованные на бесконечности или в фокальной плоскости линзы( на экране), имеющие очень малую толщину( последняя обусловлена высоким коэффициентом отражения ρ пластин); здесь не возникают дополнительные максимумы между главными максимумами. Линза I 0 Экран I 1 P
Интерференция от дифракционной решетки. Замечание. Многолучевая интерференция наблюдается и в других спектральных приборах, например: в интерферометре Фабри-1 (его еще называют эталоном Фабри-Перо, высокостабильный воздушный зазор) за счет многократного отражения лучей от параллельных, тщательно отшлифованных поверхностей, имеющих специальный отражающий слой( с ρ) при этом для интенсивностей вышедших лучей будет соблюдаться соотношение : I : I =1: ρ2: ρ4: ρ8 1 2 3 4 Не участвуют в интерферентности => В результате суперпозиции таких лучей => редкая картина> интерференционные кольца равного наклона, локализованные на бесконечности или в фокальной плоскости линзы( на экране), имеющие очень малую толщину( последняя обусловлена высоким коэффициентом отражения ρ пластин); здесь не возникают дополнительные максимумы между главными максимумами. Линза I 0 Экран I 1 P
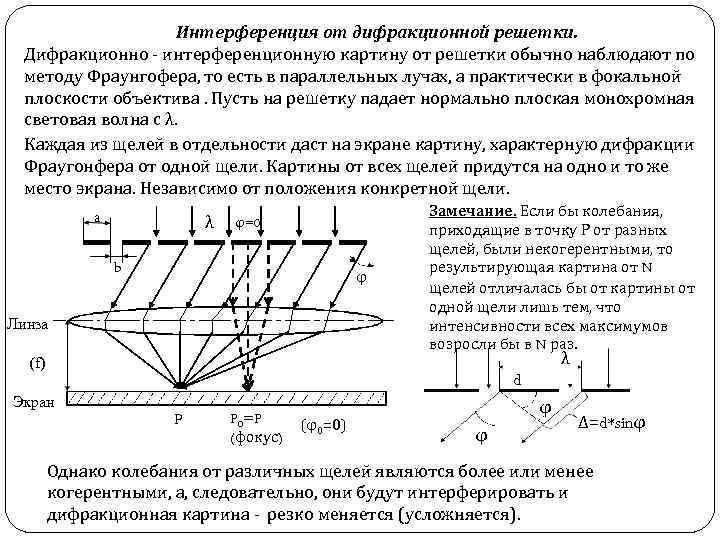 Интерференция от дифракционной решетки. Дифракционно - интерференционную картину от решетки обычно наблюдают по методу Фраунгофера, то есть в параллельных лучах, а практически в фокальной плоскости объектива. Пусть на решетку падает нормально плоская монохромная световая волна с λ. Каждая из щелей в отдельности даст на экране картину, характерную дифракции Фраугонфера от одной щели. Картины от всех щелей придутся на одно и то же место экрана. Независимо от положения конкретной щели. a λ φ=0 b φ Линза Замечание. Если бы колебания, приходящие в точку Р от разных щелей, были некогерентными, то результирующая картина от N щелей отличалась бы от картины от одной щели лишь тем, что интенсивности всех максимумов возросли бы в N раз. λ (f) d Экран P P 0=P (фокус) (φ0=0) φ φ ∆=d*sinφ Однако колебания от различных щелей являются более или менее когерентными, а, следовательно, они будут интерферировать и дифракционная картина - резко меняется (усложняется).
Интерференция от дифракционной решетки. Дифракционно - интерференционную картину от решетки обычно наблюдают по методу Фраунгофера, то есть в параллельных лучах, а практически в фокальной плоскости объектива. Пусть на решетку падает нормально плоская монохромная световая волна с λ. Каждая из щелей в отдельности даст на экране картину, характерную дифракции Фраугонфера от одной щели. Картины от всех щелей придутся на одно и то же место экрана. Независимо от положения конкретной щели. a λ φ=0 b φ Линза Замечание. Если бы колебания, приходящие в точку Р от разных щелей, были некогерентными, то результирующая картина от N щелей отличалась бы от картины от одной щели лишь тем, что интенсивности всех максимумов возросли бы в N раз. λ (f) d Экран P P 0=P (фокус) (φ0=0) φ φ ∆=d*sinφ Однако колебания от различных щелей являются более или менее когерентными, а, следовательно, они будут интерферировать и дифракционная картина - резко меняется (усложняется).
 Интерференция от дифракционной решетки. Определение: ширина решетки h(p)=N*d, где N-полное число штрихов (щелей). Замечание. В дальнейшем будем предполагать, что hког падающей волны намного больше длины(ширины) решетки т. ч. колебания от всех щелей => когерентные, то есть h ког. >> h(p). Главные максимумы: 1. В середину дифракционной картины т. P 0 -> F – фокус когерентные колебания от всех щелей приходят в фазе (при φ0=0) и, следовательно, усиливают друга. То есть, если амплитуда колебаний от одной щели равна А 1 , а число щелей N, то результирующая амплитуда А и соответствующая ей интерферентность I будут: при φ=0 => АPo =A 1 *N, IPo = I 1*N 2 2. Такой же результат получается и при углах дифракции φ, для которых оптическая разность хода ∆ (лучей) колебаний от соседних щелей равна целому числу длин волн ; при условии: Где основная формула дифракционной решетки d*sin φ= сm *λ, где m=0, 1, 2 … (1) условия главных максимумов Замечание: Здесь знаки (±) следуют из симметрии дифракционных картин относительно нормали к решетке ( для φ0=0).
Интерференция от дифракционной решетки. Определение: ширина решетки h(p)=N*d, где N-полное число штрихов (щелей). Замечание. В дальнейшем будем предполагать, что hког падающей волны намного больше длины(ширины) решетки т. ч. колебания от всех щелей => когерентные, то есть h ког. >> h(p). Главные максимумы: 1. В середину дифракционной картины т. P 0 -> F – фокус когерентные колебания от всех щелей приходят в фазе (при φ0=0) и, следовательно, усиливают друга. То есть, если амплитуда колебаний от одной щели равна А 1 , а число щелей N, то результирующая амплитуда А и соответствующая ей интерферентность I будут: при φ=0 => АPo =A 1 *N, IPo = I 1*N 2 2. Такой же результат получается и при углах дифракции φ, для которых оптическая разность хода ∆ (лучей) колебаний от соседних щелей равна целому числу длин волн ; при условии: Где основная формула дифракционной решетки d*sin φ= сm *λ, где m=0, 1, 2 … (1) условия главных максимумов Замечание: Здесь знаки (±) следуют из симметрии дифракционных картин относительно нормали к решетке ( для φ0=0).
 Интерференция от дифракционной решетки. В направлениях угла φm , определяемых формулой(1), возникающие максимумы ( m-20 порядка), интенсивность которых в N 2 –раз больше → I 1 (интенсивность одной щели в том же направлении угла φm. Их называют главными максимумами m-го порядка. Замечание. Именно главные максимумы имеют практический интерес : чем больше N штрихов содержит решетка, тем эти Imax – более узкие и резкие. Ряд замечаний: 1. При наклонном падении плоской волны на решетку под d углом i к нормали разность хода соответствующих лучей i соответствующих лучей от двух соседних щелей => i ∆= d*(sinφ – sin i) m И тогда направление на главный Imax , будут определяться из условия: φm d*(sinφm – sin i) = ± m*λ (2) Причем углы φm и i должны отчитываться в одном направлении от нормали( например по часовой стрелке). i φm φm 2. Для отражательной решетки условия (2) так же справедливо, только здесь углы φm и i – надо отсчитывать в противоположенных направлениях. d 3. Условия (1)и (2) главных фраунгоферовых максимумов являются универсальными, то есть выполняются для любой форму штриха.
Интерференция от дифракционной решетки. В направлениях угла φm , определяемых формулой(1), возникающие максимумы ( m-20 порядка), интенсивность которых в N 2 –раз больше → I 1 (интенсивность одной щели в том же направлении угла φm. Их называют главными максимумами m-го порядка. Замечание. Именно главные максимумы имеют практический интерес : чем больше N штрихов содержит решетка, тем эти Imax – более узкие и резкие. Ряд замечаний: 1. При наклонном падении плоской волны на решетку под d углом i к нормали разность хода соответствующих лучей i соответствующих лучей от двух соседних щелей => i ∆= d*(sinφ – sin i) m И тогда направление на главный Imax , будут определяться из условия: φm d*(sinφm – sin i) = ± m*λ (2) Причем углы φm и i должны отчитываться в одном направлении от нормали( например по часовой стрелке). i φm φm 2. Для отражательной решетки условия (2) так же справедливо, только здесь углы φm и i – надо отсчитывать в противоположенных направлениях. d 3. Условия (1)и (2) главных фраунгоферовых максимумов являются универсальными, то есть выполняются для любой форму штриха.
 C Интерференционные минимумы R Воспользуемся векторной диаграммой для анализа картины. Результирующая амплитуда А колебаний, приходящих в точку Р экрана представляет собой вектор, замыкающий цепочку амплитуд- векторов Аi когерентных колебаний, приходящих сюда от каждых от N щелей: А 1, А 2…Аn. По модулю эти векторы равны, а по фазе : каждый следующий отстает от предыдущего на один и тот же угол δ, который определяется через оптическую разность хода ∆ - соответствующих лучей: N*δ δ R δ (*)δ=2π Где d – период решетки При удалении т. Р от центра экрана (фокуса F линзы) будет расти угол дифракции φ, и, следовательно, ↑ - угол δ (разность фаз), цепочка векторов будет постепенно закручиваться и при определенном φ => цепочка замкнется, а результирующий вектор A→ 0; это произойдет, когда общий угол: N*δ=2π*τ Замечание: При дальнейшем росте φ: цепочка векторов будет периодически то распрямляться (появление очередного максимума), то – замыкаться (появление очередного интерферентного минимума), при чем последнее будет происходить при углах: (N*δ)=2π*m’ (3) Где - целое число, кроме 0, N, 2 N … и т. д. при этих числах => Imax Подставив в (3) значение δ из (*) => условия интерференционных минимумов дифракционной решетки: α* sinφ= ± (4) где m’ –целое число, кроме 0, N, 2 N, 3 N…
C Интерференционные минимумы R Воспользуемся векторной диаграммой для анализа картины. Результирующая амплитуда А колебаний, приходящих в точку Р экрана представляет собой вектор, замыкающий цепочку амплитуд- векторов Аi когерентных колебаний, приходящих сюда от каждых от N щелей: А 1, А 2…Аn. По модулю эти векторы равны, а по фазе : каждый следующий отстает от предыдущего на один и тот же угол δ, который определяется через оптическую разность хода ∆ - соответствующих лучей: N*δ δ R δ (*)δ=2π Где d – период решетки При удалении т. Р от центра экрана (фокуса F линзы) будет расти угол дифракции φ, и, следовательно, ↑ - угол δ (разность фаз), цепочка векторов будет постепенно закручиваться и при определенном φ => цепочка замкнется, а результирующий вектор A→ 0; это произойдет, когда общий угол: N*δ=2π*τ Замечание: При дальнейшем росте φ: цепочка векторов будет периодически то распрямляться (появление очередного максимума), то – замыкаться (появление очередного интерферентного минимума), при чем последнее будет происходить при углах: (N*δ)=2π*m’ (3) Где - целое число, кроме 0, N, 2 N … и т. д. при этих числах => Imax Подставив в (3) значение δ из (*) => условия интерференционных минимумов дифракционной решетки: α* sinφ= ± (4) где m’ –целое число, кроме 0, N, 2 N, 3 N…
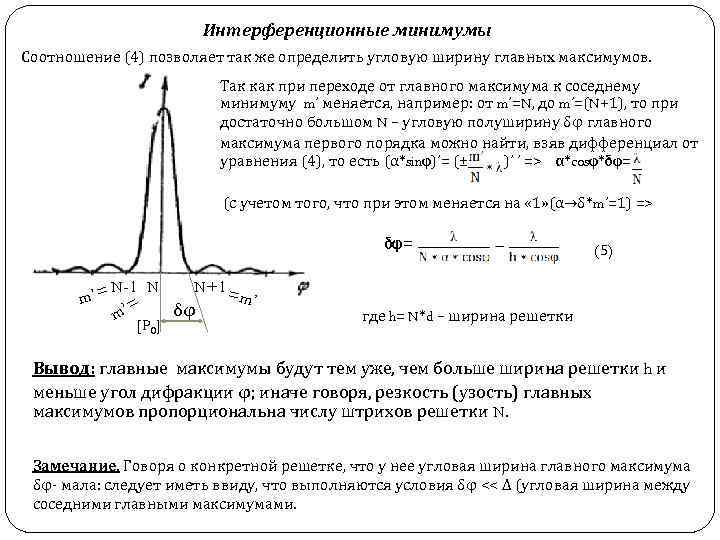 Интерференционные минимумы Соотношение (4) позволяет так же определить угловую ширину главных максимумов. Так как при переходе от главного максимума к соседнему минимуму m’ меняется, например: от m’=N, до m’=(N+1), то при достаточно большом N – угловую полуширину δφ главного максимума первого порядка можно найти, взяв дифференциал от уравнения (4), то есть (α*sinφ)’= (± )’ ’ => α*cosφ*δφ= (с учетом того, что при этом меняется на « 1» (α→δ*m’=1) => δφ= m’= N-1 N N+1 = m’ ’= δφ m [P 0] (5) где h= N*d – ширина решетки Вывод: главные максимумы будут тем уже, чем больше ширина решетки h и меньше угол дифракции φ; иначе говоря, резкость (узость) главных максимумов пропорциональна числу штрихов решетки N. Замечание. Говоря о конкретной решетке, что у нее угловая ширина главного максимума δφ- мала: следует иметь ввиду, что выполняются условия δφ << ∆ (угловая ширина между соседними главными максимумами.
Интерференционные минимумы Соотношение (4) позволяет так же определить угловую ширину главных максимумов. Так как при переходе от главного максимума к соседнему минимуму m’ меняется, например: от m’=N, до m’=(N+1), то при достаточно большом N – угловую полуширину δφ главного максимума первого порядка можно найти, взяв дифференциал от уравнения (4), то есть (α*sinφ)’= (± )’ ’ => α*cosφ*δφ= (с учетом того, что при этом меняется на « 1» (α→δ*m’=1) => δφ= m’= N-1 N N+1 = m’ ’= δφ m [P 0] (5) где h= N*d – ширина решетки Вывод: главные максимумы будут тем уже, чем больше ширина решетки h и меньше угол дифракции φ; иначе говоря, резкость (узость) главных максимумов пропорциональна числу штрихов решетки N. Замечание. Говоря о конкретной решетке, что у нее угловая ширина главного максимума δφ- мала: следует иметь ввиду, что выполняются условия δφ << ∆ (угловая ширина между соседними главными максимумами.
 Дифракционные минимумы Анализируя дифракционную картину с помощью векторной диаграммы принимали отдельные амплитуд - векторы | | = const, что преувеличение угла φ не соответствует положениям дифракции от одной щели( Ai – амплитуда колебания от i-ой щели; и она уменьшается по мере роста угла φ, а затем ведет себя по периодичному закону: Ai=A 0 , где = Следовательно, на ряду интерферентностью минимумами (4), надо иметь в виду еще и дифракционные минимумы, следовательно дифракционные минимумы, обусловленные действием отдельных щелей, которым, как известно, соответствует условию: b*sinφm=±m*λ, где b-ширина щелей решетки, m=1, 2, …. При этом условии все Ai→ 0, а значит и результирующая амплитуда в этих направлениях всегда будет равна « 0» . (даже в том случае, если этому направлению соответствует главный максимум m-ого порядка).
Дифракционные минимумы Анализируя дифракционную картину с помощью векторной диаграммы принимали отдельные амплитуд - векторы | | = const, что преувеличение угла φ не соответствует положениям дифракции от одной щели( Ai – амплитуда колебания от i-ой щели; и она уменьшается по мере роста угла φ, а затем ведет себя по периодичному закону: Ai=A 0 , где = Следовательно, на ряду интерферентностью минимумами (4), надо иметь в виду еще и дифракционные минимумы, следовательно дифракционные минимумы, обусловленные действием отдельных щелей, которым, как известно, соответствует условию: b*sinφm=±m*λ, где b-ширина щелей решетки, m=1, 2, …. При этом условии все Ai→ 0, а значит и результирующая амплитуда в этих направлениях всегда будет равна « 0» . (даже в том случае, если этому направлению соответствует главный максимум m-ого порядка).
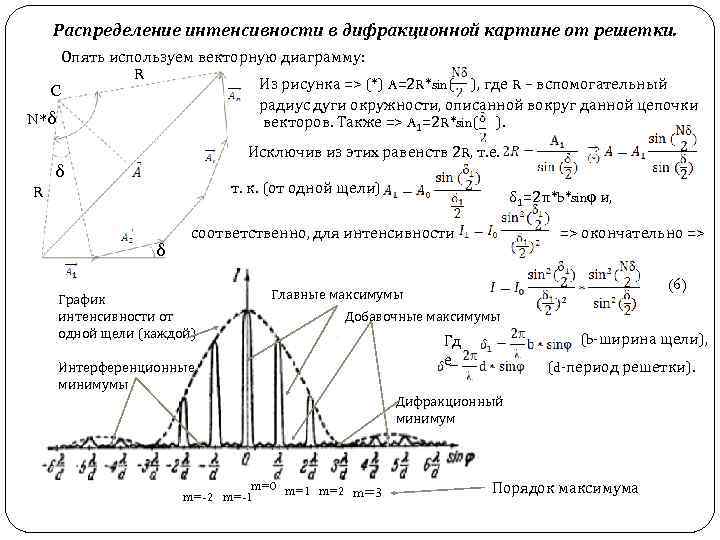 Распределение интенсивности в дифракционной картине от решетки. Опять используем векторную диаграмму: C R Из рисунка => (*) A=2 R*sin( ), где R – вспомогательный радиус дуги окружности, описанной вокруг данной цепочки векторов. Также => A 1=2 R*sin( ). N*δ Исключив из этих равенств 2 R, т. е. δ т. к. (от одной щели) R δ δ 1=2π*b*sinφ и, соответственно, для интенсивности График интенсивности от одной щели (каждой) => окончательно => (6) Главные максимумы Добавочные максимумы Интерференционные минимумы (b-ширина щели), Гд е (d-период решетки). Дифракционный минимум m=0 m=1 m=2 m=3 m=-2 m=-1 Порядок максимума
Распределение интенсивности в дифракционной картине от решетки. Опять используем векторную диаграмму: C R Из рисунка => (*) A=2 R*sin( ), где R – вспомогательный радиус дуги окружности, описанной вокруг данной цепочки векторов. Также => A 1=2 R*sin( ). N*δ Исключив из этих равенств 2 R, т. е. δ т. к. (от одной щели) R δ δ 1=2π*b*sinφ и, соответственно, для интенсивности График интенсивности от одной щели (каждой) => окончательно => (6) Главные максимумы Добавочные максимумы Интерференционные минимумы (b-ширина щели), Гд е (d-период решетки). Дифракционный минимум m=0 m=1 m=2 m=3 m=-2 m=-1 Порядок максимума
 Распределение интенсивности в дифракционной картине от решетки. Замечание: Между соседними главными Imax расположенными (N-1)интерференционных минимумов, между последними (N-2)-добавочных максимумов (при N-большом), Первая дробь в выражении (6) определяет дифракционное распределение интерференции от каждой щели решетки, вторая дробь описывает изменение интерференции при многолучевой интерференции от N – щелей. Таким образом, плавная функция I(φ) – модулирует многолучевую интерференционную картину от N – щелей. Замечание: Практически наиболее важными являются главные максимумы попадающие в центральный дифракционный максимум от каждой щели. Спектральные характеристики дифракционных решеток. В соответствии и формулой (1) положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого света, все максимумы (за исключением центрального: m=0) разложатся в спектр по длинам волн (т. е. начиная с m=1 будем иметь в каждом порядке целый набор – спектр цветных максимумов); причем наибольшее отклонение (от центра картины) в каждом порядке испытывает красная область спектра (более длинноволновая), а наименьшее – фиолетовая область.
Распределение интенсивности в дифракционной картине от решетки. Замечание: Между соседними главными Imax расположенными (N-1)интерференционных минимумов, между последними (N-2)-добавочных максимумов (при N-большом), Первая дробь в выражении (6) определяет дифракционное распределение интерференции от каждой щели решетки, вторая дробь описывает изменение интерференции при многолучевой интерференции от N – щелей. Таким образом, плавная функция I(φ) – модулирует многолучевую интерференционную картину от N – щелей. Замечание: Практически наиболее важными являются главные максимумы попадающие в центральный дифракционный максимум от каждой щели. Спектральные характеристики дифракционных решеток. В соответствии и формулой (1) положение главных максимумов зависит от длины волны λ. Поэтому при пропускании через решетку белого света, все максимумы (за исключением центрального: m=0) разложатся в спектр по длинам волн (т. е. начиная с m=1 будем иметь в каждом порядке целый набор – спектр цветных максимумов); причем наибольшее отклонение (от центра картины) в каждом порядке испытывает красная область спектра (более длинноволновая), а наименьшее – фиолетовая область.
 Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): 1. Угловая дисперсия D – характеризует степень пространственного (углового) «разнесения» (разделения линий в спектре) волн с различными λ. - по определению: дифференцируя условие главных максимумов => d*cosφ*dφ=m*dλ => (7) Замечание: Для небольших m=> D≈ , когда φ –min (cosφ=1) Вывод: Угловая дисперсия D – растет: с увеличением порядка спектра m; уменьшением периода решетки d (т. е. с увеличением числа штрихов на мм), увеличением (в определенных пределах) угла дифракции φ. 1’. Линейная дисперсия Dлин. - по определению: , где dl – линейное расстояние на фотопленке (спектрограмме) между спектральными линиями, отличающимися по длине волны на dλ. f – фокусное расстояние собирающей линзы => Dлин. =f*D (8) Замечание: Для небольших m => Dлин. ≈f* Экран (фотопластинка) Соседние спектральные линии [λ, λ+dλ]
Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): 1. Угловая дисперсия D – характеризует степень пространственного (углового) «разнесения» (разделения линий в спектре) волн с различными λ. - по определению: дифференцируя условие главных максимумов => d*cosφ*dφ=m*dλ => (7) Замечание: Для небольших m=> D≈ , когда φ –min (cosφ=1) Вывод: Угловая дисперсия D – растет: с увеличением порядка спектра m; уменьшением периода решетки d (т. е. с увеличением числа штрихов на мм), увеличением (в определенных пределах) угла дифракции φ. 1’. Линейная дисперсия Dлин. - по определению: , где dl – линейное расстояние на фотопленке (спектрограмме) между спектральными линиями, отличающимися по длине волны на dλ. f – фокусное расстояние собирающей линзы => Dлин. =f*D (8) Замечание: Для небольших m => Dлин. ≈f* Экран (фотопластинка) Соседние спектральные линии [λ, λ+dλ]
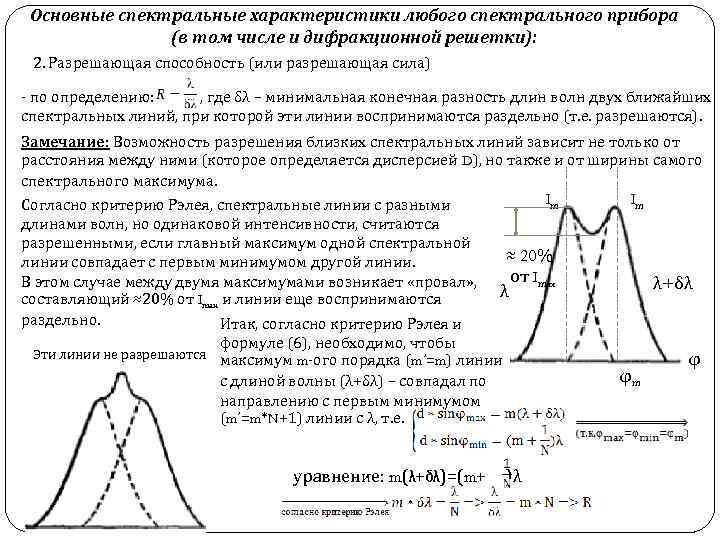 Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): 2. Разрешающая способность (или разрешающая сила) - по определению: , где δλ – минимальная конечная разность длин волн двух ближайших спектральных линий, при которой эти линии воспринимаются раздельно (т. е. разрешаются). Замечание: Возможность разрешения близких спектральных линий зависит не только от расстояния между ними (которое определяется дисперсией D), но также и от ширины самого спектрального максимума. Im Im Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, считаются разрешенными, если главный максимум одной спектральной ≈ 20% линии совпадает с первым минимумом другой линии. от Imax В этом случае между двумя максимумами возникает «провал» , λ+δλ λ составляющий ≈20% от Imax и линии еще воспринимаются раздельно. Итак, согласно критерию Рэлея и формуле (6), необходимо, чтобы Эти линии не разрешаются максимум m-ого порядка (m’=m) линии φ φm с длиной волны (λ+δλ) – совпадал по направлению с первым минимумом (m’=m*N+1) линии с λ, т. е. уравнение: m(λ+δλ)=(m+ )λ
Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): 2. Разрешающая способность (или разрешающая сила) - по определению: , где δλ – минимальная конечная разность длин волн двух ближайших спектральных линий, при которой эти линии воспринимаются раздельно (т. е. разрешаются). Замечание: Возможность разрешения близких спектральных линий зависит не только от расстояния между ними (которое определяется дисперсией D), но также и от ширины самого спектрального максимума. Im Im Согласно критерию Рэлея, спектральные линии с разными длинами волн, но одинаковой интенсивности, считаются разрешенными, если главный максимум одной спектральной ≈ 20% линии совпадает с первым минимумом другой линии. от Imax В этом случае между двумя максимумами возникает «провал» , λ+δλ λ составляющий ≈20% от Imax и линии еще воспринимаются раздельно. Итак, согласно критерию Рэлея и формуле (6), необходимо, чтобы Эти линии не разрешаются максимум m-ого порядка (m’=m) линии φ φm с длиной волны (λ+δλ) – совпадал по направлению с первым минимумом (m’=m*N+1) линии с λ, т. е. уравнение: m(λ+δλ)=(m+ )λ
 Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): Вывод: Разрешающая сила дифракционной решетки пропорциональна порядку спектра m и числу щелей N. Формула (8) определяет верхний предел разрешающей способности R; она справедлива при следующих условиях: 1) Интенсивность обоих максимумов – одинакова; 2) Уширение линий должно быть обусловлено только дифракцией; 3) Падающий на решетку свет должен иметь ширину когерентности hког. >(N*d) ; только в этом случае все N – щелей (штрихов) решетки будут действовать согласованно (когерентно). 3. Область дисперсии - ∆λ – это ширина спектрального интервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный прибор становится непригодным для исследования соответствующего участка спектра. Длинноволновый участок спектра (m+1)-ого порядка, если m(λ+∆λ)=(m+1)λ, откуда => что область дисперсии ∆λ= (9) , т. е. область дисперсии ∆λ. Таким образом, при работе со спектрами низких порядков (обычно до 3 -го порядка) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал. Замечание: В этом главное преимущество дифракционных решеток перед интерференционными спектральными приборами, например перед интерферометром Фабри-Перо, у которого из-за очень высоких порядков (m) – область дисперсии очень мала.
Основные спектральные характеристики любого спектрального прибора (в том числе и дифракционной решетки): Вывод: Разрешающая сила дифракционной решетки пропорциональна порядку спектра m и числу щелей N. Формула (8) определяет верхний предел разрешающей способности R; она справедлива при следующих условиях: 1) Интенсивность обоих максимумов – одинакова; 2) Уширение линий должно быть обусловлено только дифракцией; 3) Падающий на решетку свет должен иметь ширину когерентности hког. >(N*d) ; только в этом случае все N – щелей (штрихов) решетки будут действовать согласованно (когерентно). 3. Область дисперсии - ∆λ – это ширина спектрального интервала, при которой еще нет перекрытия спектров соседних порядков. Если спектры соседних порядков перекрываются, то спектральный прибор становится непригодным для исследования соответствующего участка спектра. Длинноволновый участок спектра (m+1)-ого порядка, если m(λ+∆λ)=(m+1)λ, откуда => что область дисперсии ∆λ= (9) , т. е. область дисперсии ∆λ. Таким образом, при работе со спектрами низких порядков (обычно до 3 -го порядка) дифракционная решетка пригодна для исследования излучения, занимающего достаточно широкий спектральный интервал. Замечание: В этом главное преимущество дифракционных решеток перед интерференционными спектральными приборами, например перед интерферометром Фабри-Перо, у которого из-за очень высоких порядков (m) – область дисперсии очень мала.
 Дифракция на пространственной решетке. Ранее нами изучалась дифракционная картина от одномерной периодической структуры, которой является обычная плоская дифракционная решетка. Определение: Решетки, имеющие две системы взаимно перпендикулярных штрихов, относятся к двумерным периодическим структурам. d 2 Экран (фотопленка) λ d 1 В этом случае от вертикальных штрихов следует обычная дифракционная картина максимумов, соответствующих условию: α 1*sinφ1= ±m 1*λ; (m 1=0, 1, 2, …), а горизонтальные штрихи «разобьют» каждые образовавшиеся дифрагированные пучки (в горизонтальном направлении) – на систему расположенных уже в вертикальном направлении – максимумов, удовлетворяющих условию: α 2*sinφ2= ±m 2*λ (m 2=0, 1, 2, …). В итоге => дифракционная картина, имеющая вид правильно расположенных пятен, каждому из которых соответствует два целочисленных индекса: m 1 и m 2.
Дифракция на пространственной решетке. Ранее нами изучалась дифракционная картина от одномерной периодической структуры, которой является обычная плоская дифракционная решетка. Определение: Решетки, имеющие две системы взаимно перпендикулярных штрихов, относятся к двумерным периодическим структурам. d 2 Экран (фотопленка) λ d 1 В этом случае от вертикальных штрихов следует обычная дифракционная картина максимумов, соответствующих условию: α 1*sinφ1= ±m 1*λ; (m 1=0, 1, 2, …), а горизонтальные штрихи «разобьют» каждые образовавшиеся дифрагированные пучки (в горизонтальном направлении) – на систему расположенных уже в вертикальном направлении – максимумов, удовлетворяющих условию: α 2*sinφ2= ±m 2*λ (m 2=0, 1, 2, …). В итоге => дифракционная картина, имеющая вид правильно расположенных пятен, каждому из которых соответствует два целочисленных индекса: m 1 и m 2.
 Дифракция на пространственной решетке. Дифракция наблюдается также и на 3 -х мерных периодических структурах, т. е. таких пространственных образованиях, обнаруживающих периодичность неоднородностей по 3 -м не лежащим в одной плоскости направлениям (например, x, y, z). A 3 d 1 d 2 A 1 d 3 A 2 A 4 Определение: Такими структурами являются все кристаллические тела (т. е. их пространственная кристаллическая решетка). Эту пространственную решетку можно представить как совокупность равноотстоящих параллельных одномерных периодических структур (система атомов), расположенных вдоль одной из координатных осей. Однако, характерные значения периодов (d 1, d 2, т. е. примерно несколько d 3) пространственной решетки , что не согласуется с длинами волн видимого света в плане создания обязательных условий дифракции (α ). Это условие выполняется для рентгеновских лучей, у которых λ (и может быть еще меньше). Для рентгеновских лучей кристаллы служат естественными дифракционными решетками.
Дифракция на пространственной решетке. Дифракция наблюдается также и на 3 -х мерных периодических структурах, т. е. таких пространственных образованиях, обнаруживающих периодичность неоднородностей по 3 -м не лежащим в одной плоскости направлениям (например, x, y, z). A 3 d 1 d 2 A 1 d 3 A 2 A 4 Определение: Такими структурами являются все кристаллические тела (т. е. их пространственная кристаллическая решетка). Эту пространственную решетку можно представить как совокупность равноотстоящих параллельных одномерных периодических структур (система атомов), расположенных вдоль одной из координатных осей. Однако, характерные значения периодов (d 1, d 2, т. е. примерно несколько d 3) пространственной решетки , что не согласуется с длинами волн видимого света в плане создания обязательных условий дифракции (α ). Это условие выполняется для рентгеновских лучей, у которых λ (и может быть еще меньше). Для рентгеновских лучей кристаллы служат естественными дифракционными решетками.
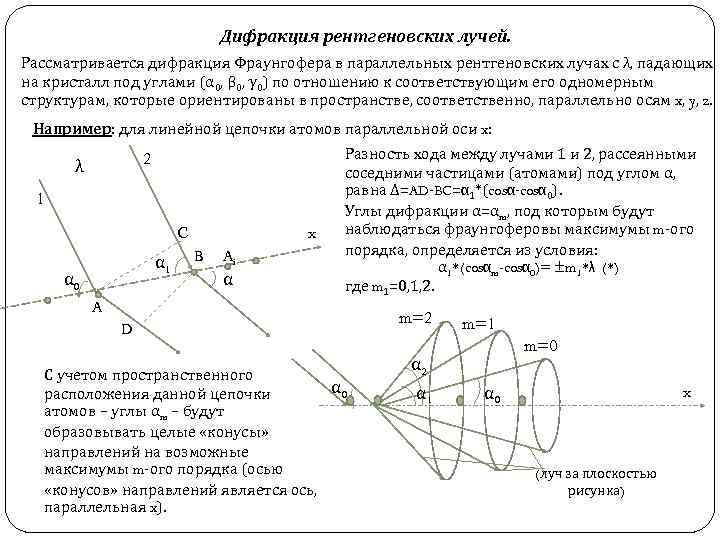 Дифракция рентгеновских лучей. Рассматривается дифракция Фраунгофера в параллельных рентгеновских лучах с λ, падающих на кристалл под углами (α 0, β 0, γ 0) по отношению к соответствующим его одномерным структурам, которые ориентированы в пространстве, соответственно, параллельно осям x, y, z. Например: для линейной цепочки атомов параллельной оси x: 2 λ 1 C α 1 α 0 A x B Ai α Разность хода между лучами 1 и 2, рассеянными соседними частицами (атомами) под углом α, равна ∆=AD-BC=α 1*(cosα-cosα 0). Углы дифракции α=αm, под которым будут наблюдаться фраунгоферовы максимумы m-ого порядка, определяется из условия: α 1*(cosαm-cosα 0)= ±m 1*λ (*) где m 1=0, 1, 2. D С учетом пространственного α 0 расположения данной цепочки атомов – углы αm – будут образовывать целые «конусы» направлений на возможные максимумы m-ого порядка (осью «конусов» направлений является ось, параллельная x). m=2 m=1 m=0 α 2 α 1 α 0 x (луч за плоскостью рисунка)
Дифракция рентгеновских лучей. Рассматривается дифракция Фраунгофера в параллельных рентгеновских лучах с λ, падающих на кристалл под углами (α 0, β 0, γ 0) по отношению к соответствующим его одномерным структурам, которые ориентированы в пространстве, соответственно, параллельно осям x, y, z. Например: для линейной цепочки атомов параллельной оси x: 2 λ 1 C α 1 α 0 A x B Ai α Разность хода между лучами 1 и 2, рассеянными соседними частицами (атомами) под углом α, равна ∆=AD-BC=α 1*(cosα-cosα 0). Углы дифракции α=αm, под которым будут наблюдаться фраунгоферовы максимумы m-ого порядка, определяется из условия: α 1*(cosαm-cosα 0)= ±m 1*λ (*) где m 1=0, 1, 2. D С учетом пространственного α 0 расположения данной цепочки атомов – углы αm – будут образовывать целые «конусы» направлений на возможные максимумы m-ого порядка (осью «конусов» направлений является ось, параллельная x). m=2 m=1 m=0 α 2 α 1 α 0 x (луч за плоскостью рисунка)
 Дифракция рентгеновских лучей Аналогично (*) можно записать условия Imax-ов для периодических структур (цепочек атомов), параллельных осям y и z. Таким образом, при наклонном падении рентгеновского параллельного пучка на кристаллическую решетку (имеющую прямоугольное сечение) будут наблюдаться главные максимумы фраунгоферовой дифракции. При соблюдении, так называемых условий Лауэ (немецкий физик 1913 г. ) (10) Где Углы α 0, β 0, γ 0, и α, β, γ – углы между осями координат x, y, z и направлениями распространения падающего и дифрагированного пучков, соответственно. Следует учитывать, что углы α, β, γ не являются независимыми и в случае прямоугольной системы координат должны удовлетворять соотношению: (11) Система уравнений (10) и (11) оказывается разрешима лишь для некоторых, вполне определенных длин волн λ, и именно каждому такому значению λ будут соответствовать свой максимум (и направления αm, βm). Замечание: т. к. разность косинусов в (10) по модулю не может превышать « 2» , то сами условия Лауэ могут быть выполнены при m 1; 2; 3 - лишь в том случае, если λ. Если же длина волны λ будет больше максимальной разности хода лучей от соседних узлов решетки (т. е. λ ), то дифракционные минимумы будут отсутствовать (за исключением нулевого mi=0), и излучение с такой λ будет распространяться в среде без рассеяния, не испытывая дифракции.
Дифракция рентгеновских лучей Аналогично (*) можно записать условия Imax-ов для периодических структур (цепочек атомов), параллельных осям y и z. Таким образом, при наклонном падении рентгеновского параллельного пучка на кристаллическую решетку (имеющую прямоугольное сечение) будут наблюдаться главные максимумы фраунгоферовой дифракции. При соблюдении, так называемых условий Лауэ (немецкий физик 1913 г. ) (10) Где Углы α 0, β 0, γ 0, и α, β, γ – углы между осями координат x, y, z и направлениями распространения падающего и дифрагированного пучков, соответственно. Следует учитывать, что углы α, β, γ не являются независимыми и в случае прямоугольной системы координат должны удовлетворять соотношению: (11) Система уравнений (10) и (11) оказывается разрешима лишь для некоторых, вполне определенных длин волн λ, и именно каждому такому значению λ будут соответствовать свой максимум (и направления αm, βm). Замечание: т. к. разность косинусов в (10) по модулю не может превышать « 2» , то сами условия Лауэ могут быть выполнены при m 1; 2; 3 - лишь в том случае, если λ. Если же длина волны λ будет больше максимальной разности хода лучей от соседних узлов решетки (т. е. λ ), то дифракционные минимумы будут отсутствовать (за исключением нулевого mi=0), и излучение с такой λ будет распространяться в среде без рассеяния, не испытывая дифракции.
 Метод Вульфа-Бреггов. Русский кристаллофизик Ю. В. Вульф и английский физик У. Г. Брегги и У. А. Брегги в 1913 г. Независимо показали, что дифракцию ренгеновских лучей на кристаллической решетке можно рассматривать как результат интерференции отраженных X- лучей (зеркальным образом) от системы параллельных кристаллический плоскостей – атомных слоев, отстоящих друг от друга на расстояниях d. Замечание: Вторичные волны, отразившись от разных атомных плоскостей – когерентны и будут интерферировать между собой. Если при этом разность хода лучей, отразившихся от λ соседних слоев ∆=ABC=2 d*sinα (здесь угол α принято называть углом скольжения) будет соответствовать целому числу длин волн т. е. α α A α B C 2 d*sinα= ±m*λ (формула Вульфа-Бреггов) (12) Где m=1, 2, 3…, то в соответствующих направлениях возникают максимумы. Замечание: формула (12) может быть получена также как следствие из условия Лауэ. В кристалле можно провести множество систем атомных плоскостей в различных направлениях и каждая система может дать максимум, если для нее выполнено условие (12). Однако заметную интенсивность дают только те плоскости, в которых атомы расположены наиболее плотно.
Метод Вульфа-Бреггов. Русский кристаллофизик Ю. В. Вульф и английский физик У. Г. Брегги и У. А. Брегги в 1913 г. Независимо показали, что дифракцию ренгеновских лучей на кристаллической решетке можно рассматривать как результат интерференции отраженных X- лучей (зеркальным образом) от системы параллельных кристаллический плоскостей – атомных слоев, отстоящих друг от друга на расстояниях d. Замечание: Вторичные волны, отразившись от разных атомных плоскостей – когерентны и будут интерферировать между собой. Если при этом разность хода лучей, отразившихся от λ соседних слоев ∆=ABC=2 d*sinα (здесь угол α принято называть углом скольжения) будет соответствовать целому числу длин волн т. е. α α A α B C 2 d*sinα= ±m*λ (формула Вульфа-Бреггов) (12) Где m=1, 2, 3…, то в соответствующих направлениях возникают максимумы. Замечание: формула (12) может быть получена также как следствие из условия Лауэ. В кристалле можно провести множество систем атомных плоскостей в различных направлениях и каждая система может дать максимум, если для нее выполнено условие (12). Однако заметную интенсивность дают только те плоскости, в которых атомы расположены наиболее плотно.
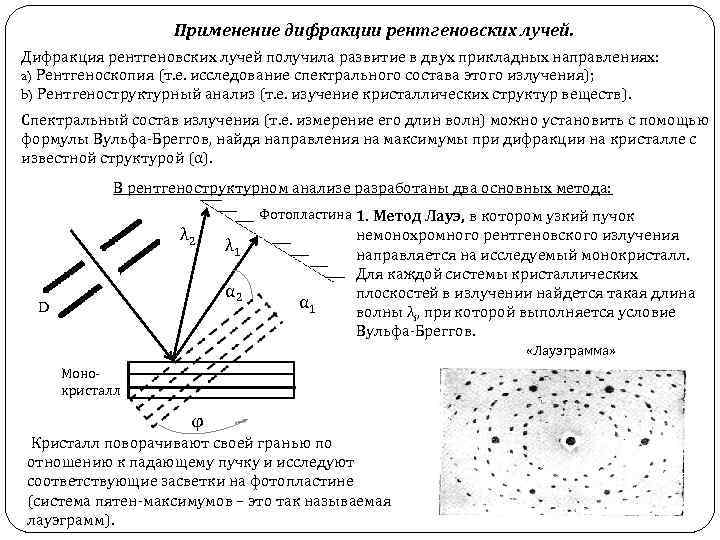 Применение дифракции рентгеновских лучей. Дифракция рентгеновских лучей получила развитие в двух прикладных направлениях: a) Рентгеноскопия (т. е. исследование спектрального состава этого излучения); b) Рентгеноструктурный анализ (т. е. изучение кристаллических структур веществ). Спектральный состав излучения (т. е. измерение его длин волн) можно установить с помощью формулы Вульфа-Бреггов, найдя направления на максимумы при дифракции на кристалле с известной структурой (α). В рентгеноструктурном анализе разработаны два основных метода: λ 2 Фотопластина 1. Метод Лауэ, в котором узкий пучок λ 1 α 2 D α 1 немонохромного рентгеновского излучения направляется на исследуемый монокристалл. Для каждой системы кристаллических плоскостей в излучении найдется такая длина волны λi, при которой выполняется условие Вульфа-Бреггов. «Лауэграмма» Монокристалл φ Кристалл поворачивают своей гранью по отношению к падающему пучку и исследуют соответствующие засветки на фотопластине (система пятен-максимумов – это так называемая лауэграмм).
Применение дифракции рентгеновских лучей. Дифракция рентгеновских лучей получила развитие в двух прикладных направлениях: a) Рентгеноскопия (т. е. исследование спектрального состава этого излучения); b) Рентгеноструктурный анализ (т. е. изучение кристаллических структур веществ). Спектральный состав излучения (т. е. измерение его длин волн) можно установить с помощью формулы Вульфа-Бреггов, найдя направления на максимумы при дифракции на кристалле с известной структурой (α). В рентгеноструктурном анализе разработаны два основных метода: λ 2 Фотопластина 1. Метод Лауэ, в котором узкий пучок λ 1 α 2 D α 1 немонохромного рентгеновского излучения направляется на исследуемый монокристалл. Для каждой системы кристаллических плоскостей в излучении найдется такая длина волны λi, при которой выполняется условие Вульфа-Бреггов. «Лауэграмма» Монокристалл φ Кристалл поворачивают своей гранью по отношению к падающему пучку и исследуют соответствующие засветки на фотопластине (система пятен-максимумов – это так называемая лауэграмм).
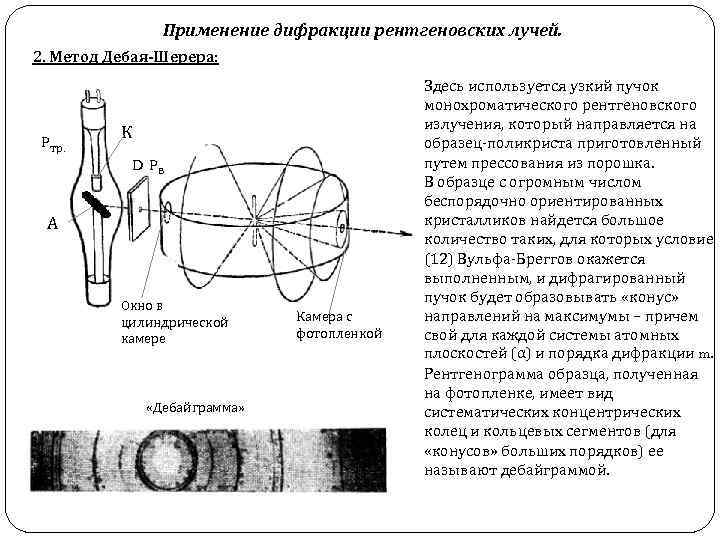 Применение дифракции рентгеновских лучей. 2. Метод Дебая-Шерера: Pтр. К D Pв А Окно в цилиндрической камере «Дебайграмма» Камера с фотопленкой Здесь используется узкий пучок монохроматического рентгеновского излучения, который направляется на образец-поликриста приготовленный путем прессования из порошка. В образце с огромным числом беспорядочно ориентированных кристалликов найдется большое количество таких, для которых условие (12) Вульфа-Бреггов окажется выполненным, и дифрагированный пучок будет образовывать «конус» направлений на максимумы – причем свой для каждой системы атомных плоскостей (α) и порядка дифракции m. Рентгенограмма образца, полученная на фотопленке, имеет вид систематических концентрических колец и кольцевых сегментов (для «конусов» больших порядков) ее называют дебайграммой.
Применение дифракции рентгеновских лучей. 2. Метод Дебая-Шерера: Pтр. К D Pв А Окно в цилиндрической камере «Дебайграмма» Камера с фотопленкой Здесь используется узкий пучок монохроматического рентгеновского излучения, который направляется на образец-поликриста приготовленный путем прессования из порошка. В образце с огромным числом беспорядочно ориентированных кристалликов найдется большое количество таких, для которых условие (12) Вульфа-Бреггов окажется выполненным, и дифрагированный пучок будет образовывать «конус» направлений на максимумы – причем свой для каждой системы атомных плоскостей (α) и порядка дифракции m. Рентгенограмма образца, полученная на фотопленке, имеет вид систематических концентрических колец и кольцевых сегментов (для «конусов» больших порядков) ее называют дебайграммой.


