Лекция 2 Закономерности случайной вариации Оценка достоверности статистических

Лекция 2 Закономерности случайной вариации. Оценка достоверности статистических параметров

Вероятность и статистическая закономерность l l Каждое отдельное явление, взятое само по себе, представляется случайным, но, взятые в массе, они обнаруживают определенную, так называемую статистическую закономерность Вероятность – это возможность осуществления определенного события в некотором количестве случаев из общего числа возможных Процесс осуществления явления на основе его вероятности называется вероятностным или стохастическим процессом. Математически – вероятность (р), есть частное от деления числа благоприятных случаев (m) на число всех равновозможных случаев (N). Вероятность варьирует от 0 до 1. 2

Теорема сложения вероятностей l l l Относится к таким независимым друг от друга событиям, которые совершенно несовместимы В общем виде, если события представить в виде множества А и В, то суммой событий называют объединение этих множеств Например, на клумбе растут 20 красных, 30 синих и 40 белых астр. Какова вероятность сорвать в темноте окрашенную (синюю или красную) астру? (ответ 0, 56) 3

Теорема умножения вероятностей l l Относится к таким независимым событиям, которые следуют друг за другом и также независимы друг от друга. Для умножения вероятностей необходимо, чтобы второе событие осуществлялось только при осуществлении первого события, при этом оба события осуществляются независимо друг от друга Например, какова вероятность наличия цифры 4 у двух выброшенных одновременно кубиков (ответ 1/36) Если события представить как множества А и В, то произведением событий является пересечение множеств 4

Распределение вероятностей l l случайная переменная «х» принимает разные значения: х1, х2, х3 , …, хn под влиянием разнообразных и независимых причин, то есть, её вариация случайная Отдельным значениям xi можно придать соответствующие вероятности: р1, р2, р3 , …, pn Совокупность значений xi и соответствующих им вероятностей pi и называется распределением 5

Биномиальное распределение l l l l Если вероятности появления отдельных значений xi выражаются величинами, соответствующими коэффициентам разложения бинома Ньютона, распределение называется биномиальным: (a+b)1=a+b 1: 1 (a+b)2=a 2+2 ab+b 2 1: 2: 1 (a+b)3=a 3+3 a 2 b+3 ab 2+b 3 1: 3: 3: 1 (a+b)4=a 4+4 a 3 b+6 a 2 b 2+4 ab 3+b 4 1: 4: 6: 4: 1 Биномиальное распределение относится к признакам, варьирующим дискретно, прерывисто. Частоты отдельных классов распределения пропорциональны коэффициентам разложения бинома Ньютона: (p+q)k, где р - вероятность появления данного события, q – вероятность непоявления, k число классов При биномиальном распределении средняя арифметическая и среднее квадратическое отклонение вычисляются по следующим формулам: 6

Распределение Пуассона l l l Распределение Пуассона, подобно биномиальному, относится к дискретной или прерывистой изменчивости. Его можно рассматривать как предельный случай биномиального. При биномиальном распределении значения «p» и «q» могут быть близки другу, при пуассоновом же «р» очень мало, то есть события осуществляются очень редко, а «q» приближается к единице. В биологии пуассонову распределению удовлетворяют редко наблюдаемые события Пуассоново распределение характеризуется только одним параметром – средней арифметической. Дисперсия обычно равна среднему или близка к нему Средняя арифметическая в распределении Пуассона обозначается λ и вычисляется по формуле: 7

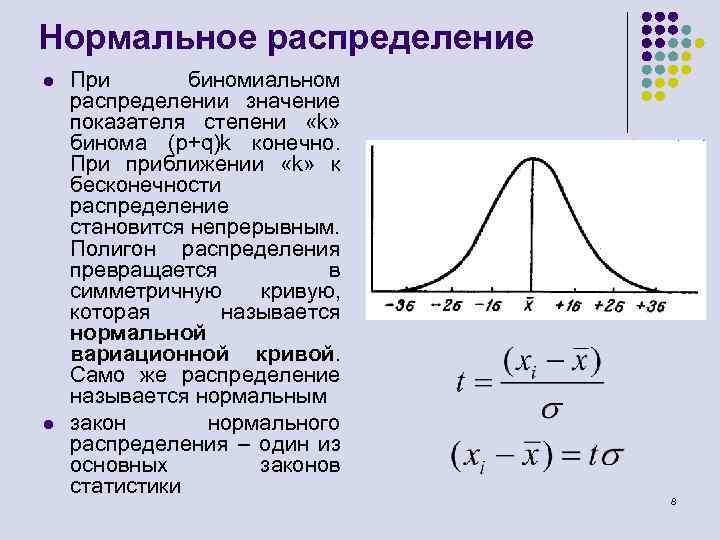Нормальное распределение l l При биномиальном распределении значение показателя степени «k» бинома (p+q)k конечно. При приближении «k» к бесконечности распределение становится непрерывным. Полигон распределения превращается в симметричную кривую, которая называется нормальной вариационной кривой. Само же распределение называется нормальным закон нормального распределения – один из основных законов статистики 8

Доверительные вероятности l l l В биометрии существенно важны 2 вероятности: 0, 95 и 0, 99. Эти вероятности получили название доверительных вероятностей С вероятностью 0, 95 любая случайно взятая варианта будет отклоняться от среднего арифметического не более чем на ± 1, 96σ, иными словами, с вероятностью 0, 05 варианта будет за пределами ± 1, 96σ. С вероятностью 0, 99 любая случайно взятая варианта будет отклоняться от среднего арифметического не более чем на ± 2, 58σ, иными словами, с вероятностью 0, 01 варианта будет за пределами ± 2, 58σ. Доверительная вероятность 0, 99 соответствует более высокому уровню вероятности, соответственно 0, 95 более низкому. Доверительные вероятности определяют доверительный интервал между границами варьирования параметров генеральной совокупности 9

Уровни значимости l l l Определенным значениям вероятностей соответствуют так называемые уровни значимости Вероятности 0, 95 (95%) соответствует уровень значимости 0, 05 (5%). Это означает, что выход за пределы принятых границ возможен с вероятностью 0, 05, то есть, вероятность ошибочного прогноза составляет 5% Вероятности 0, 99 (99%) соответствует уровень значимости 0, 01 (1%). Это означает, что выход за пределы принятых границ возможен с вероятностью 0, 01, то есть, вероятность ошибочного прогноза составляет 1% Уровень значимости 0, 01 более высокий, 0, 05 – более низкий Наивысший уровень значимости 0, 001 (0, 1%) соответствует доверительной вероятности 0, 999 (99, 9%) 10

Проблема достоверности в статистике l l Проблема достоверности состоит в расхождении между статистическими показателями выборки и статистическими показателями генеральной совокупности Если статистические показатели выборки близки к статистическим показателям генеральной совокупности – их достоверность считается высокой Если статистические показатели выборки сильно отличаются от показателей генеральной совокупности – они недостоверны. Выборка должна быть репрезентативной, то есть она должна формироваться на основе случайного отбора вариант. Существуют специальные методы позволяющие оценить степень репрезентативности выборки 11

Ошибка репрезентативности средней арифметической l l l Распределение выборочных средних вокруг генерального среднего близко к нормальному закону Среднее квадратическое отклонение выборочных средних вокруг генерального называется средней ошибкой (средней квадратической ошибкой, стандартной ошибкой, ошибкой выборочности, ошибкой репрезентативности), чем меньше эта ошибка, тем ближе выборочное среднее к генеральному среднему. Ошибка средней ( ) вычисляется по формуле: 12

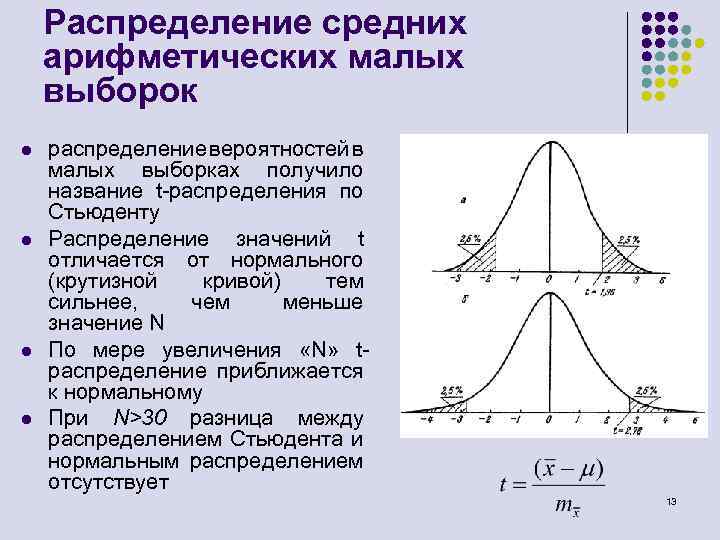Распределение средних арифметических малых выборок l l распределение вероятностей в малых выборках получило название t-распределения по Стьюденту Распределение значений t отличается от нормального (крутизной кривой) тем сильнее, чем меньше значение N По мере увеличения «N» tраспределение приближается к нормальному При N>30 разница между распределением Стьюдента и нормальным распределением отсутствует 13

Доверительный интервал средней арифметической генеральной совокупности l l Для определения доверительного интервала μ необходимо знать: среднюю арифметическую выборки, ошибку средней и критерий Стьюдента определенного уровня значимости (t 01 или t 05) Если N>30 вместо значения t берётся нормальный интеграл вероятности, если N<30 берется t из таблицы Стьюдента 14

Определение необходимого объема выборочной совокупности l l Для определения необходимого объема выборки необходимо задать следующие параметры: 1) желаемую точность (Δ) – допустимое расхождение между средней арифметической выборки и средней арифметической генеральной совокупности; 2) коэффициент Стьюдента для определенной доверительной вероятности; 3) среднее квадратическое отклонение (σ): 15

Ошибка репрезентативности и доверительный интервал для среднего квадратического отклонения и коэффициента вариации 16

Нулевая гипотеза l l l Общие принципы сравнения выборок основываются на анализе так называемой нулевой гипотезы (Н 0) Согласно этой гипотезе, первоначально принимается, что между показателями разных выборок достоверного различия нет Задача статистического анализа заключается либо в принятии нулевой гипотезы, либо в её отклонении. Отбрасывание или принятие нулевой гипотезы связано с принятием того или иного уровня достоверности утверждений (значимости). Существует и противоположная нулевой – альтернативная гипотеза (Н 1), смысл которой противоположен 17

Два типа статистических ошибок и мощность статистического критерия l l Ошибка первого рода (ошибка α-типа): отклоняется нулевая гипотеза, которая в действительности верная Ошибка второго рода (ошибка β-типа): принимается нулевая гипотеза, которая в действительности ложная Мощность статистического критерия есть вероятность того, что будет принято правильное решение при ложной нулевой гипотезе (1 -β) Мощность критерия зависит от объема выборки, уровня значимости, направленности нулевой и альтернативной гипотез, надежности экспериментальных методов и приборов 18

Оценка достоверности различий между выборочными средними арифметическими l l l Разница между средними арифметическими генеральных совокупностей всегда достоверна, даже если она очень мала, поскольку эти средние были вычислены для генеральных совокупностей Для установления достоверности разницы между средними арифметическими используют нормированные отклонения (t): Нулевая гипотеза отвергается, если разница между средними арифметическими достоверна, то есть, критерий Стьюдента будет больше стандартного значения (tst) при определенном уровне значимости 19