172__13.02.12.ppt
- Количество слайдов: 27
 Лекція № 2 з дисципліни “Медична інформатика” для студентів ІІ курсу медичних факультетів
Лекція № 2 з дисципліни “Медична інформатика” для студентів ІІ курсу медичних факультетів
 План лекції План 1. Основні поняття статистики 2. Закони випадкових величин
План лекції План 1. Основні поняття статистики 2. Закони випадкових величин
 Основні поняття та визначення Статистика – це наука, яка вивчає статистичні методи збирання, опрацювання, подання, аналізу та інтерпретації даних. Стан організму пацієнта характеризується сукупністю властивостей (АТ, температура, рівень еритроцитів, лейкоцитів…) Параметри – властивості, які піддаються оцінці у будьякій формі якісній або кількісній. Приклад, рівень глюкози у крові пацієнта становить 5, 58 ммоль/л
Основні поняття та визначення Статистика – це наука, яка вивчає статистичні методи збирання, опрацювання, подання, аналізу та інтерпретації даних. Стан організму пацієнта характеризується сукупністю властивостей (АТ, температура, рівень еритроцитів, лейкоцитів…) Параметри – властивості, які піддаються оцінці у будьякій формі якісній або кількісній. Приклад, рівень глюкози у крові пацієнта становить 5, 58 ммоль/л
 Основні поняття та визначення Випадкова величина – величина, яка в результаті величина експерименту може набути певне значення (Х 1, Х 2, . . , Хn), яке заздалегідь невідоме. Приклад, кількість пацієнтів, які відвідали поліклініку 25. 01. 12 (34 пацієнта); рівень тиреотропного гормону (0, 0078 m. TU/ml). Дискретною випадковою величиною називається величина, яка може набути лише окремі, ізольовані одне від одного значення. Неперервною випадковою величиною називається величина, яка може набути довільного значення із проміжку (будь-які числа). Приклад, кількість пацієнтів, Приклад, , 1) рівень тиреотропного гормону (0, 0078 які відвідали поліклініку m. TU/ml). 2) Вага 25. 01. 12 (34 пацієнта); новонародженої дитини (3, 5)
Основні поняття та визначення Випадкова величина – величина, яка в результаті величина експерименту може набути певне значення (Х 1, Х 2, . . , Хn), яке заздалегідь невідоме. Приклад, кількість пацієнтів, які відвідали поліклініку 25. 01. 12 (34 пацієнта); рівень тиреотропного гормону (0, 0078 m. TU/ml). Дискретною випадковою величиною називається величина, яка може набути лише окремі, ізольовані одне від одного значення. Неперервною випадковою величиною називається величина, яка може набути довільного значення із проміжку (будь-які числа). Приклад, кількість пацієнтів, Приклад, , 1) рівень тиреотропного гормону (0, 0078 які відвідали поліклініку m. TU/ml). 2) Вага 25. 01. 12 (34 пацієнта); новонародженої дитини (3, 5)
 Основні поняття та визначення Генеральна сукупність – сукупність, яка складається з усіх одиниць спостереження. Приклад, кількість усіх хворих на туберкульоз у світі Статистична сукупність – сукупність, яка складається з певного числа відносно однорідних елементів, взятих разом у певних межах простору і часу. Приклади кількість хворих на туберкульоз у 2010 році у Києві. Вибіркова сукупність (вибірка) – це частина генеральної або статистичної сукупності, яка відображає основні її характеристики.
Основні поняття та визначення Генеральна сукупність – сукупність, яка складається з усіх одиниць спостереження. Приклад, кількість усіх хворих на туберкульоз у світі Статистична сукупність – сукупність, яка складається з певного числа відносно однорідних елементів, взятих разом у певних межах простору і часу. Приклади кількість хворих на туберкульоз у 2010 році у Києві. Вибіркова сукупність (вибірка) – це частина генеральної або статистичної сукупності, яка відображає основні її характеристики.
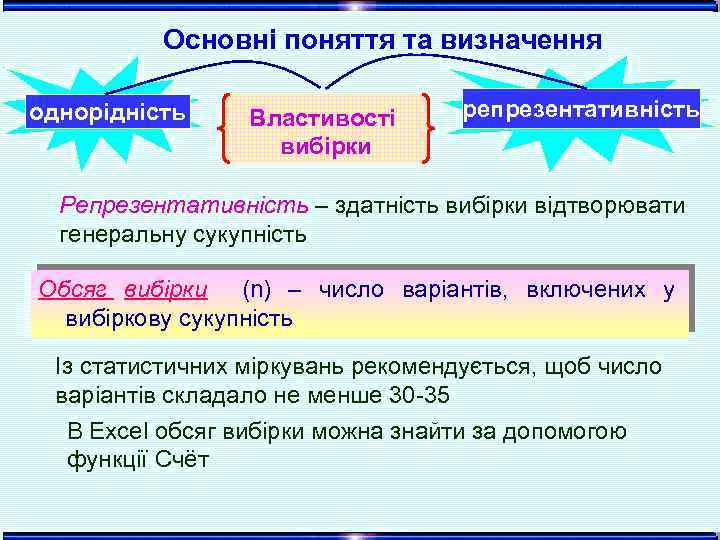 Основні поняття та визначення однорідність Властивості вибірки репрезентативність Репрезентативність – здатність вибірки відтворювати Репрезентативність генеральну сукупність Обсяг вибірки (n) – число варіантів, включених у вибіркову сукупність Із статистичних міркувань рекомендується, щоб число варіантів складало не менше 30 -35 В Excel обсяг вибірки можна знайти за допомогою функції Счёт
Основні поняття та визначення однорідність Властивості вибірки репрезентативність Репрезентативність – здатність вибірки відтворювати Репрезентативність генеральну сукупність Обсяг вибірки (n) – число варіантів, включених у вибіркову сукупність Із статистичних міркувань рекомендується, щоб число варіантів складало не менше 30 -35 В Excel обсяг вибірки можна знайти за допомогою функції Счёт
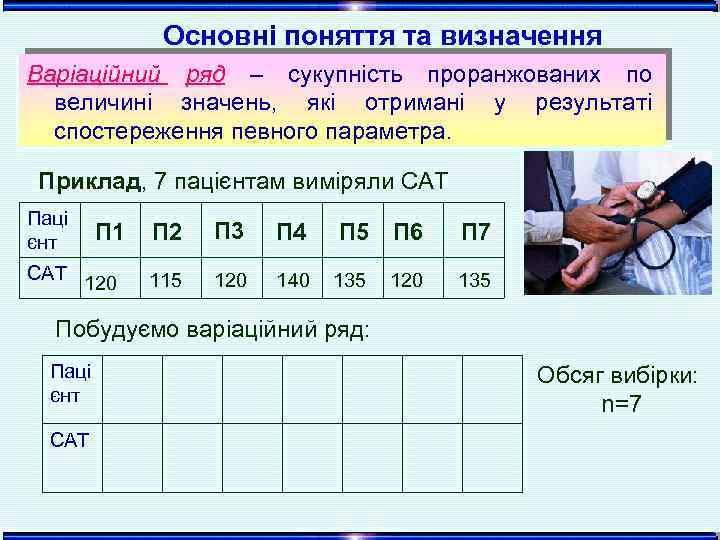 Основні поняття та визначення Варіаційний ряд – сукупність проранжованих по величині значень, які отримані у результаті спостереження певного параметра. Приклад, 7 пацієнтам виміряли САТ Паці єнт П 1 САТ 120 П 2 П 3 П 4 П 5 П 6 П 7 115 120 140 135 120 Побудуємо варіаційний ряд: Паці єнт САТ Обсяг вибірки: n=7
Основні поняття та визначення Варіаційний ряд – сукупність проранжованих по величині значень, які отримані у результаті спостереження певного параметра. Приклад, 7 пацієнтам виміряли САТ Паці єнт П 1 САТ 120 П 2 П 3 П 4 П 5 П 6 П 7 115 120 140 135 120 Побудуємо варіаційний ряд: Паці єнт САТ Обсяг вибірки: n=7
 Основні поняття та визначення Варіанти – складові варіаційного ряду. Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140 Приклад, 115, 120, 135, 140 Середні величини – узагальнюючі числові характеристики однорідних величин, які за допомогою одного числа характеризують варіаційний ряд.
Основні поняття та визначення Варіанти – складові варіаційного ряду. Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140 Приклад, 115, 120, 135, 140 Середні величини – узагальнюючі числові характеристики однорідних величин, які за допомогою одного числа характеризують варіаційний ряд.
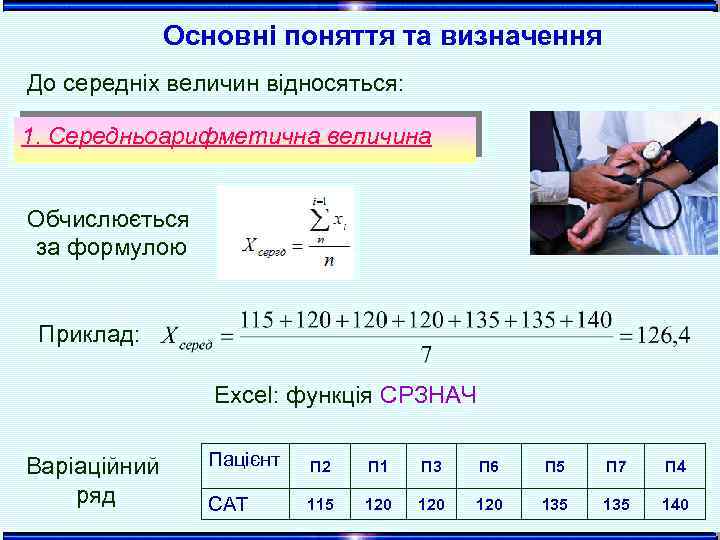 Основні поняття та визначення До середніх величин відносяться: 1. Середньоарифметична величина Обчислюється за формулою Приклад: Excel: функція СРЗНАЧ Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
Основні поняття та визначення До середніх величин відносяться: 1. Середньоарифметична величина Обчислюється за формулою Приклад: Excel: функція СРЗНАЧ Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
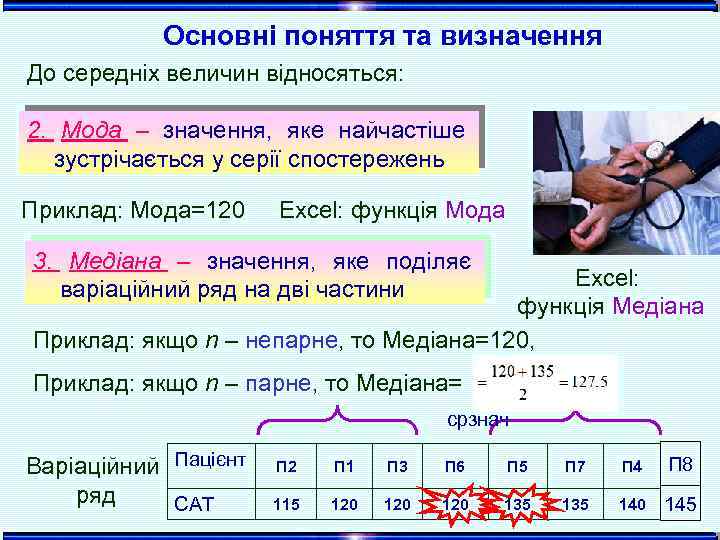 Основні поняття та визначення До середніх величин відносяться: 2. Мода – значення, яке найчастіше зустрічається у серії спостережень Приклад: Мода=120 Excel: функція Мода 3. Медіана – значення, яке поділяє варіаційний ряд на дві частини Excel: функція Медіана Приклад: якщо n – непарне, то Медіана=120, Приклад: якщо n – парне, то Медіана= срзнач Варіаційний Пацієнт ряд САТ П 2 П 1 П 3 П 6 П 5 П 7 П 4 П 8 115 120 120 135 140 145
Основні поняття та визначення До середніх величин відносяться: 2. Мода – значення, яке найчастіше зустрічається у серії спостережень Приклад: Мода=120 Excel: функція Мода 3. Медіана – значення, яке поділяє варіаційний ряд на дві частини Excel: функція Медіана Приклад: якщо n – непарне, то Медіана=120, Приклад: якщо n – парне, то Медіана= срзнач Варіаційний Пацієнт ряд САТ П 2 П 1 П 3 П 6 П 5 П 7 П 4 П 8 115 120 120 135 140 145
 Основні поняття та визначення Частота – абсолютна чисельність окремих варіант у сукупності, яка вказує на те, скільки разів зустрічається певна варіанта у варіаційному ряді. Приклад: 115 – 1 раз 120 – 3 рази 135 – 2 рази 140 – 1 раз Варіаційний ряд Excel: функція ЧАСТОТА або СЧЁТЕСЛИ Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
Основні поняття та визначення Частота – абсолютна чисельність окремих варіант у сукупності, яка вказує на те, скільки разів зустрічається певна варіанта у варіаційному ряді. Приклад: 115 – 1 раз 120 – 3 рази 135 – 2 рази 140 – 1 раз Варіаційний ряд Excel: функція ЧАСТОТА або СЧЁТЕСЛИ Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
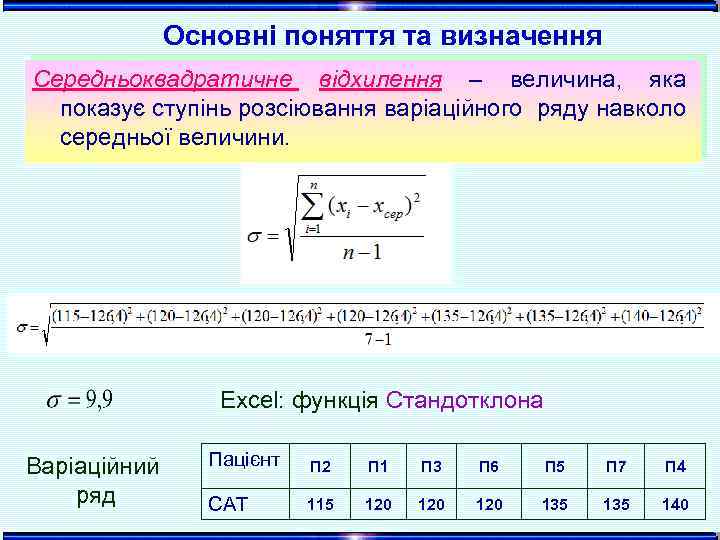 Основні поняття та визначення Середньоквадратичне відхилення – величина, яка показує ступінь розсіювання варіаційного ряду навколо середньої величини. Excel: функція Стандотклона Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
Основні поняття та визначення Середньоквадратичне відхилення – величина, яка показує ступінь розсіювання варіаційного ряду навколо середньої величини. Excel: функція Стандотклона Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
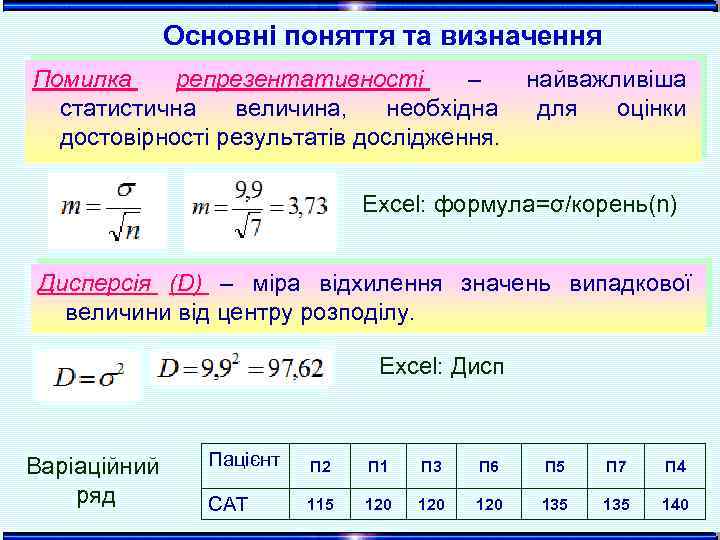 Основні поняття та визначення Помилка репрезентативності – найважливіша статистична величина, необхідна для оцінки достовірності результатів дослідження. Excel: формула=σ/корень(n) Дисперсія (D) – міра відхилення значень випадкової величини від центру розподілу. Excel: Дисп Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
Основні поняття та визначення Помилка репрезентативності – найважливіша статистична величина, необхідна для оцінки достовірності результатів дослідження. Excel: формула=σ/корень(n) Дисперсія (D) – міра відхилення значень випадкової величини від центру розподілу. Excel: Дисп Варіаційний ряд Пацієнт П 2 П 1 П 3 П 6 П 5 П 7 П 4 САТ 115 120 120 135 140
 Основні поняття та визначення Довірчий інтервал – інтервал, у межах якого із заданою довірчою ймовірністю можна очікувати значення оцінюючої випадкової величини. Кореляція (кореляційна залежність) – статистичний взаємозв'язок двох або декількох випадкових величин. При цьому зміни однієї або декількох величин, призводить до зміни іншої. Коефіцієнт кореляції – це число, значення і величина якого характеризує напрямок і силу зв'язку. Значення коефіцієнта кореляції може змінюватися від -1 до +1 Excel: Коррел
Основні поняття та визначення Довірчий інтервал – інтервал, у межах якого із заданою довірчою ймовірністю можна очікувати значення оцінюючої випадкової величини. Кореляція (кореляційна залежність) – статистичний взаємозв'язок двох або декількох випадкових величин. При цьому зміни однієї або декількох величин, призводить до зміни іншої. Коефіцієнт кореляції – це число, значення і величина якого характеризує напрямок і силу зв'язку. Значення коефіцієнта кореляції може змінюватися від -1 до +1 Excel: Коррел
 Основні поняття та визначення • Знак коефіцієнта кореляції вказує на напрям – прямий чи зворотній взаємозв’язок між двома змінними. • Абсолютне значення коефіцієнта кореляції характеризує силу та щільність взаємозв’язку, що розглядається.
Основні поняття та визначення • Знак коефіцієнта кореляції вказує на напрям – прямий чи зворотній взаємозв’язок між двома змінними. • Абсолютне значення коефіцієнта кореляції характеризує силу та щільність взаємозв’язку, що розглядається.
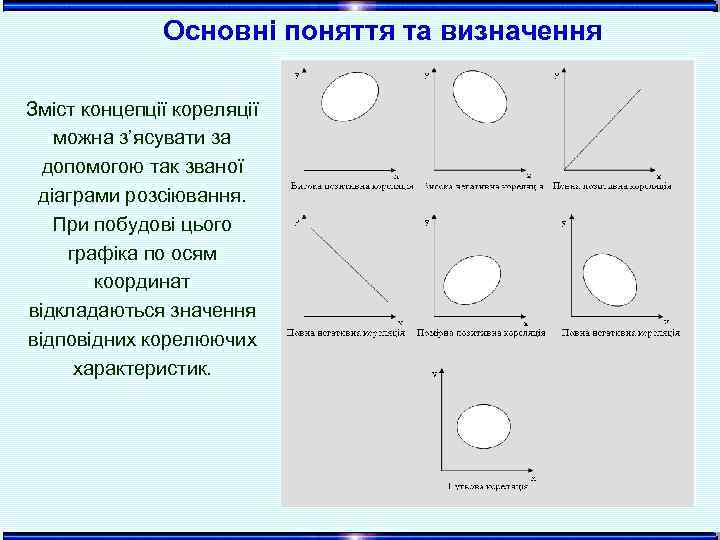 Основні поняття та визначення Зміст концепції кореляції можна з’ясувати за допомогою так званої діаграми розсіювання. При побудові цього графіка по осям координат відкладаються значення відповідних корелюючих характеристик.
Основні поняття та визначення Зміст концепції кореляції можна з’ясувати за допомогою так званої діаграми розсіювання. При побудові цього графіка по осям координат відкладаються значення відповідних корелюючих характеристик.
 Основні поняття та визначення Ймовірністю – (лат. probabilitas, англ. probability) —випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0 ≤ m ≤ n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω: n – число всіх елементарних подій, m – число елементарних подій, що сприяють появі події А Приклад. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться 1) число кратне 3. 2) число 5? Розв’язання. Число всіх елементарних подій для цього експерименту n = 6. Нехай подія В — поява на грані числа, кратного 3. Число елементарних подій, що сприяють появі В, дорівнює двом (m = 2). Отже, P(B)=m/n=2/6=1/3. Відповідь: 1/3. 2) m=1, n=6. Отже, P(C)=m/n=1/6. Відповідь: 1/6.
Основні поняття та визначення Ймовірністю – (лат. probabilitas, англ. probability) —випадкової події А називається невід’ємне число Р(А), що дорівнює відношенню числа елементарних подій m (0 ≤ m ≤ n), які сприяють появі А, до кількості всіх елементарних подій n простору Ω: n – число всіх елементарних подій, m – число елементарних подій, що сприяють появі події А Приклад. Гральний кубик підкидають один раз. Яка ймовірність того, що на грані кубика з’явиться 1) число кратне 3. 2) число 5? Розв’язання. Число всіх елементарних подій для цього експерименту n = 6. Нехай подія В — поява на грані числа, кратного 3. Число елементарних подій, що сприяють появі В, дорівнює двом (m = 2). Отже, P(B)=m/n=2/6=1/3. Відповідь: 1/3. 2) m=1, n=6. Отже, P(C)=m/n=1/6. Відповідь: 1/6.
 Основні поняття та визначення Імовірність достовірної події (це подія про яку заздалегідь відомо, що вона повинна відбутися напевно) дорівнює 1. Імовірність неможливої події (це подія про яку заздалегідь відомо, що вона відбутися не може) дорівнює 0. Імовірність випадкової величини є позитивним числом, що міститься між нулем та одиницею
Основні поняття та визначення Імовірність достовірної події (це подія про яку заздалегідь відомо, що вона повинна відбутися напевно) дорівнює 1. Імовірність неможливої події (це подія про яку заздалегідь відомо, що вона відбутися не може) дорівнює 0. Імовірність випадкової величини є позитивним числом, що міститься між нулем та одиницею
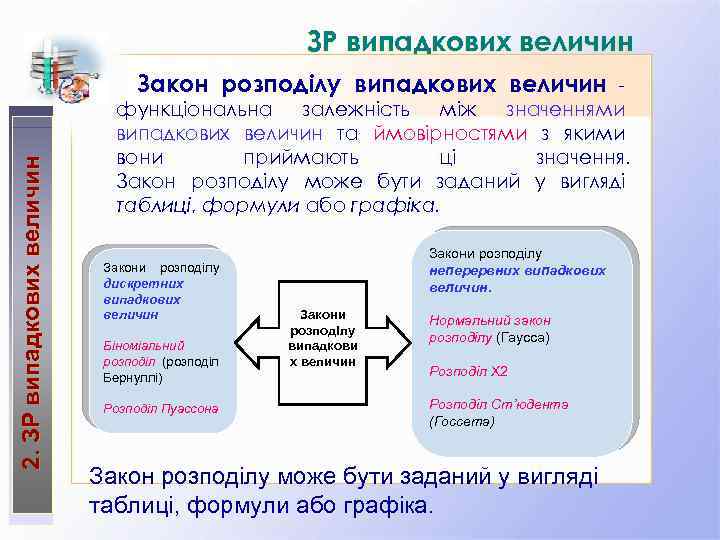 ЗР випадкових величин 2. ЗР випадкових величин Закон розподілу випадкових величин функціональна залежність між значеннями випадкових величин та ймовірностями з якими вони приймають ці значення. Закон розподілу може бути заданий у вигляді таблиці, формули або графіка. Закони розподілу дискретних випадкових величин Біноміальний розподіл (розподіл Бернуллі) Розподіл Пуассона Закони розподілу неперервних випадкових величин. Закони розподілу випадкови х величин Нормальний закон розподілу (Гаусса) Розподіл Х 2 Розподіл Ст’юдента (Госсета) Закон розподілу може бути заданий у вигляді таблиці, формули або графіка.
ЗР випадкових величин 2. ЗР випадкових величин Закон розподілу випадкових величин функціональна залежність між значеннями випадкових величин та ймовірностями з якими вони приймають ці значення. Закон розподілу може бути заданий у вигляді таблиці, формули або графіка. Закони розподілу дискретних випадкових величин Біноміальний розподіл (розподіл Бернуллі) Розподіл Пуассона Закони розподілу неперервних випадкових величин. Закони розподілу випадкови х величин Нормальний закон розподілу (Гаусса) Розподіл Х 2 Розподіл Ст’юдента (Госсета) Закон розподілу може бути заданий у вигляді таблиці, формули або графіка.
 ЗР випадкових величин • Функція розподілу – це функція F(x), котра задає ймовірність того, що випадкова величина Х приймає у випробовуванні прийме значення менше х: F(x)=Р(Х<х). Її називають інтегральною функцією. • Функція розподілу неперервної випадкової величини F(x) є неспадною неперервною функцією. Для дискретних випадкових величин функція розподілу є розривною ступеневою функцією. • Щільність розподілу для неперервної випадкової величини – це похідна від функції розподілу • Параметри розподілу: математичне сподівання, дисперсія.
ЗР випадкових величин • Функція розподілу – це функція F(x), котра задає ймовірність того, що випадкова величина Х приймає у випробовуванні прийме значення менше х: F(x)=Р(Х<х). Її називають інтегральною функцією. • Функція розподілу неперервної випадкової величини F(x) є неспадною неперервною функцією. Для дискретних випадкових величин функція розподілу є розривною ступеневою функцією. • Щільність розподілу для неперервної випадкової величини – це похідна від функції розподілу • Параметри розподілу: математичне сподівання, дисперсія.
 2. 1. ЗР дискретних ВВ Біноміальний розподіл (розподіл Бернуллі) Біноміальному закону розподілу підпорядковуються випадкові події такі, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо
2. 1. ЗР дискретних ВВ Біноміальний розподіл (розподіл Бернуллі) Біноміальному закону розподілу підпорядковуються випадкові події такі, як число викликів швидкої допомоги за певний проміжок часу, черги до лікаря в поліклініці, епідемії тощо
 ЗР дискретних ВВ Розподіл Пуассона, як граничний біноміальний використовується при вирішенні задач надійності медичного обладнання та апаратури, розповсюдження епідемії, викликів до хворого дільничих лікарів та в інших задачах масового обслуговування.
ЗР дискретних ВВ Розподіл Пуассона, як граничний біноміальний використовується при вирішенні задач надійності медичного обладнання та апаратури, розповсюдження епідемії, викликів до хворого дільничих лікарів та в інших задачах масового обслуговування.
 ЗР дискретних ВВ Приклад Вакцина формує імунітет від деякого захворювання з ймовірністю 0, 999. Провакциновано 4000 мешканців міста. Яка ймовірність того, що двоє з них не набули імунітету.
ЗР дискретних ВВ Приклад Вакцина формує імунітет від деякого захворювання з ймовірністю 0, 999. Провакциновано 4000 мешканців міста. Яка ймовірність того, що двоє з них не набули імунітету.
 2. 2. ЗР неперервних ВВ Нормальний закон розподілу (Гаусса) Нормальному закону розподілу підпорядковуються такі випадкові величини як частота дихання, частота серцевих скорочень, динаміка росту популяції тощо.
2. 2. ЗР неперервних ВВ Нормальний закон розподілу (Гаусса) Нормальному закону розподілу підпорядковуються такі випадкові величини як частота дихання, частота серцевих скорочень, динаміка росту популяції тощо.
 ЗР неперервних ВВ Розподіл
ЗР неперервних ВВ Розподіл
 ЗР неперервних ВВ Розподіл Ст’юдента
ЗР неперервних ВВ Розподіл Ст’юдента
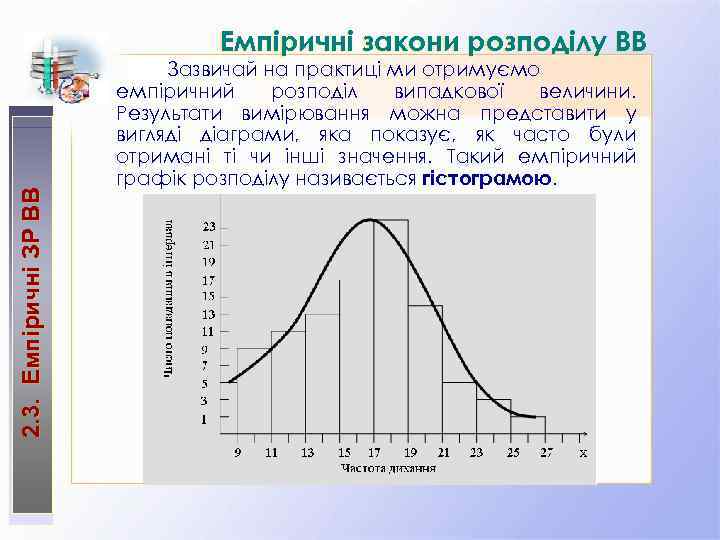 ВВ 2. 3. Емпіричні ЗР ВВ Емпіричні закони розподілу ВВ Зазвичай на практиці ми отримуємо емпіричний розподіл випадкової величини. Результати вимірювання можна представити у вигляді діаграми, яка показує, як часто були отримані ті чи інші значення. Такий емпіричний графік розподілу називається гістограмою.
ВВ 2. 3. Емпіричні ЗР ВВ Емпіричні закони розподілу ВВ Зазвичай на практиці ми отримуємо емпіричний розподіл випадкової величини. Результати вимірювання можна представити у вигляді діаграми, яка показує, як часто були отримані ті чи інші значення. Такий емпіричний графік розподілу називається гістограмою.


