Лекция 2 Виды Проецирование точки Виды

Лекция № 2 Виды. Проецирование точки

Виды Изображение – это графическое изображение предмета в определенном масштабе, выполненное установленным способом проецирования при соблюдении основных правил и служащее для определения необходимых геометрических свойств предмета.

Изображения на чертеже в зависимости от их содержания делятся на виды, разрезы и сечения. Вид – это изображение детали (части ее), обращенной к наблюдателю. Основные изображения предмета получают на гранях стеклянного куба, внутри которого помещен предмет.

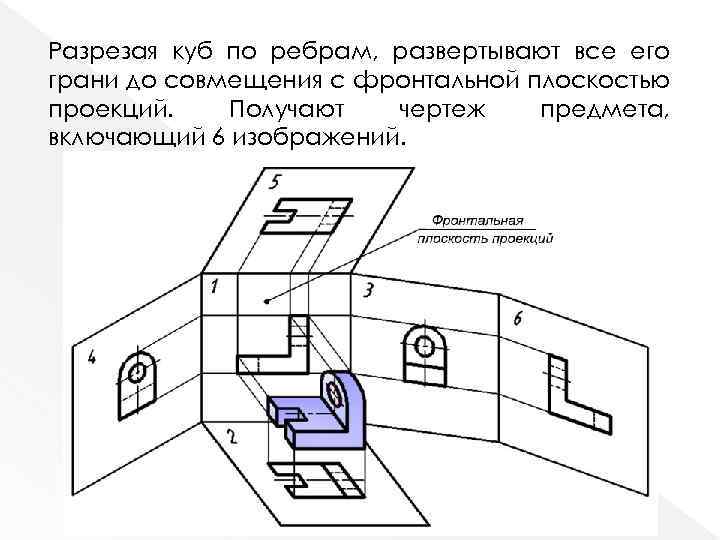Разрезая куб по ребрам, развертывают все его грани до совмещения с фронтальной плоскостью проекций. Получают чертеж предмета, включающий 6 изображений.

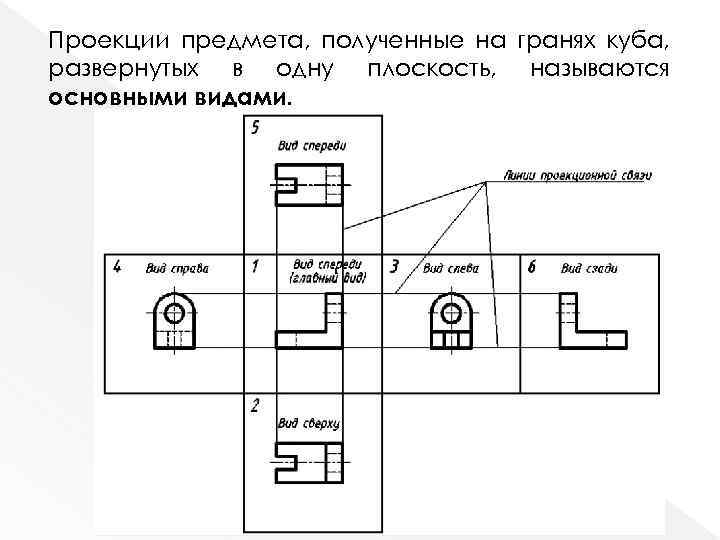Проекции предмета, полученные на гранях куба, развернутых в одну плоскость, называются основными видами.

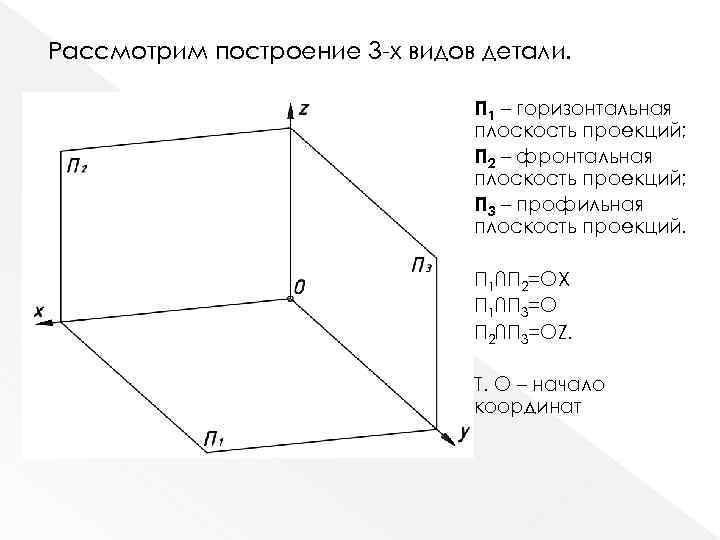Рассмотрим построение 3 -х видов детали. П 1 – горизонтальная плоскость проекций; П 2 – фронтальная плоскость проекций; П 3 – профильная плоскость проекций. П 1∩П 2=ОХ П 1∩П 3=О П 2∩П 3=ОZ. Т. О – начало координат

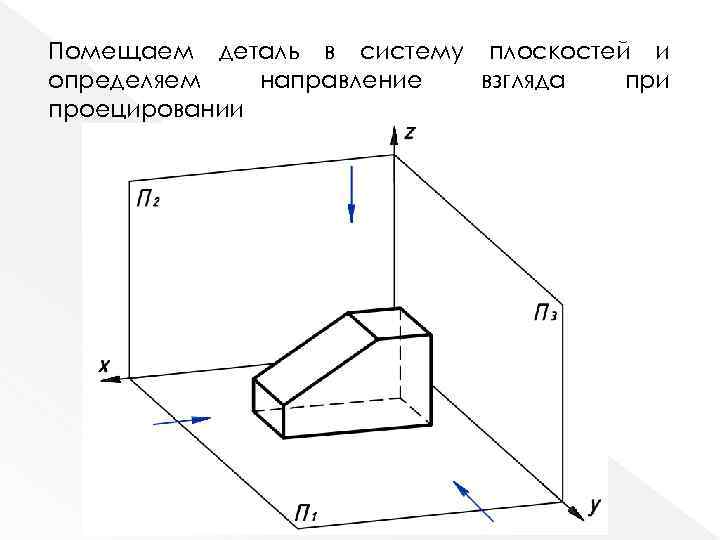Помещаем деталь в систему плоскостей и определяем направление взгляда при проецировании

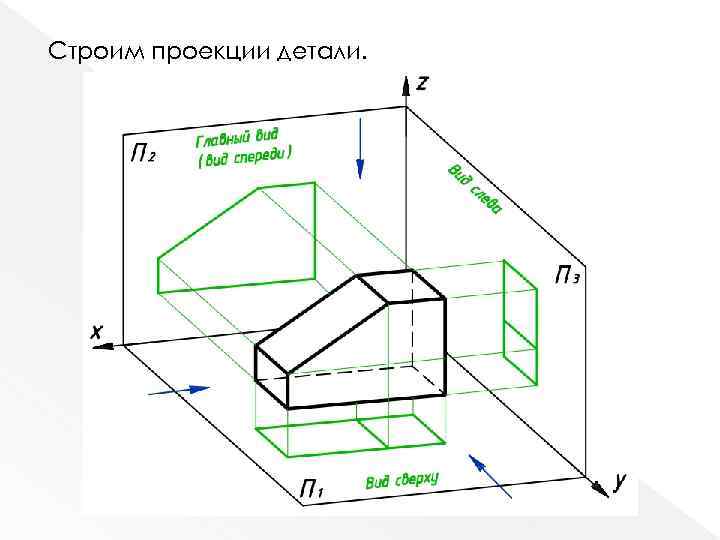Строим проекции детали.

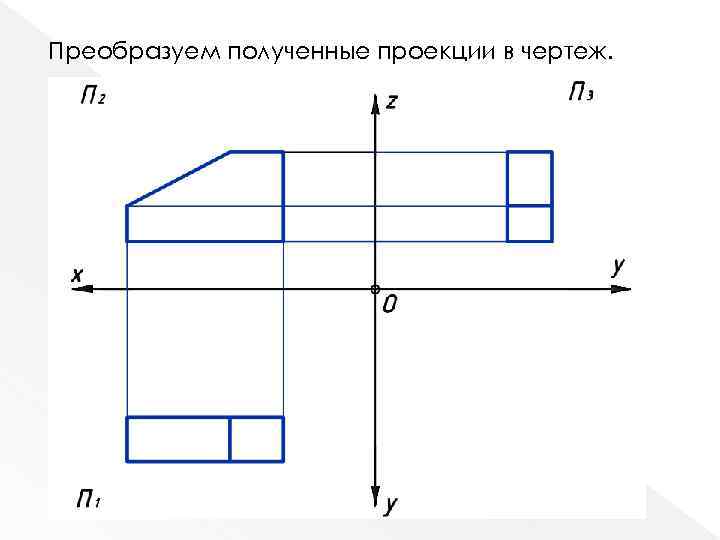Преобразуем полученные проекции в чертеж.

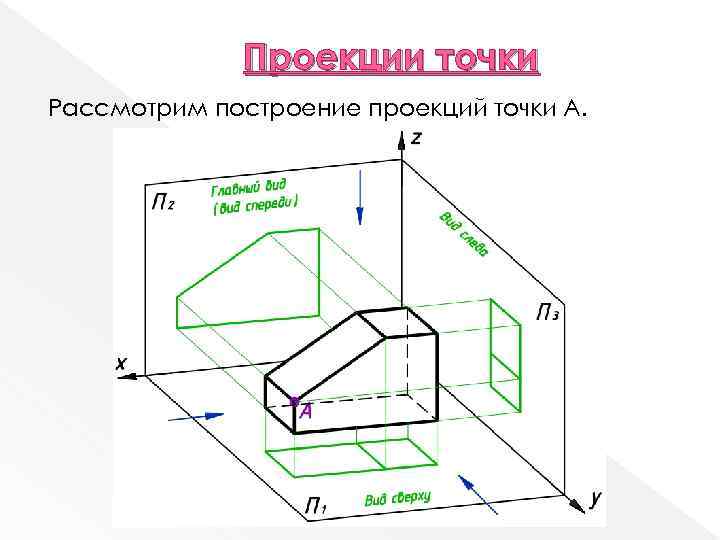Проекции точки Рассмотрим построение проекций точки А.

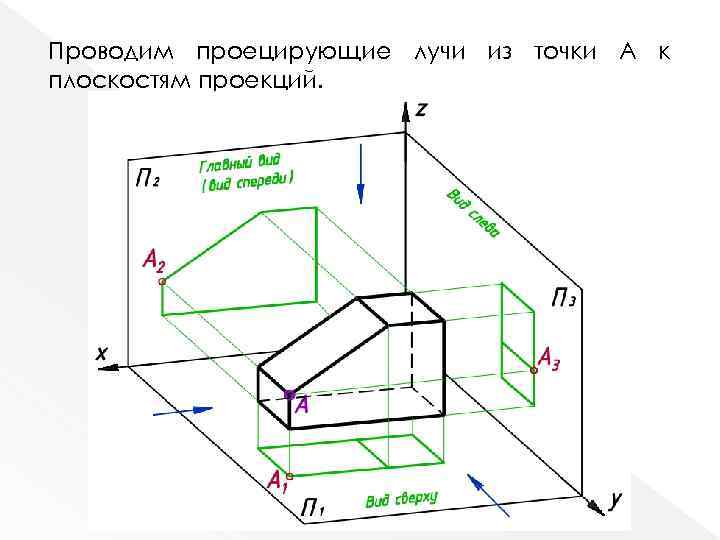Проводим проецирующие лучи из точки А к плоскостям проекций.

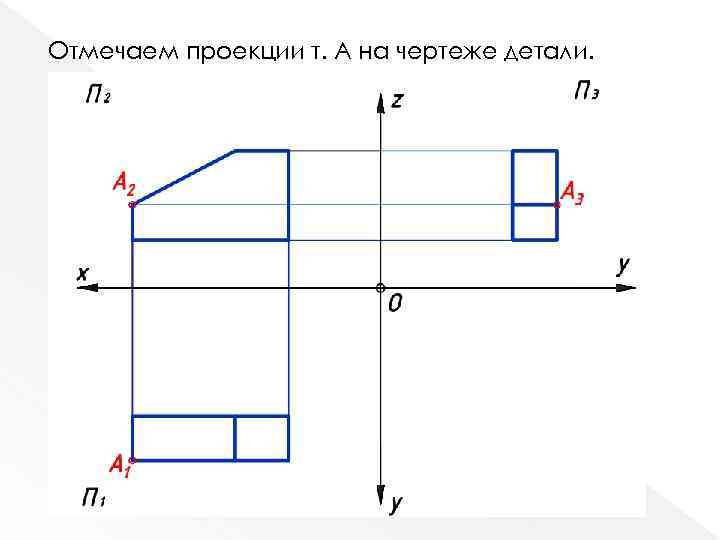Отмечаем проекции т. А на чертеже детали.

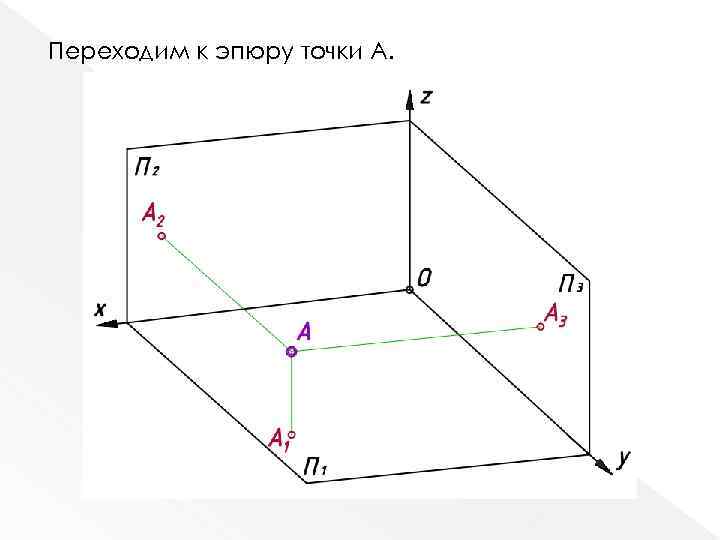
Переходим к эпюру точки А.

Переходим к эпюру точки А.

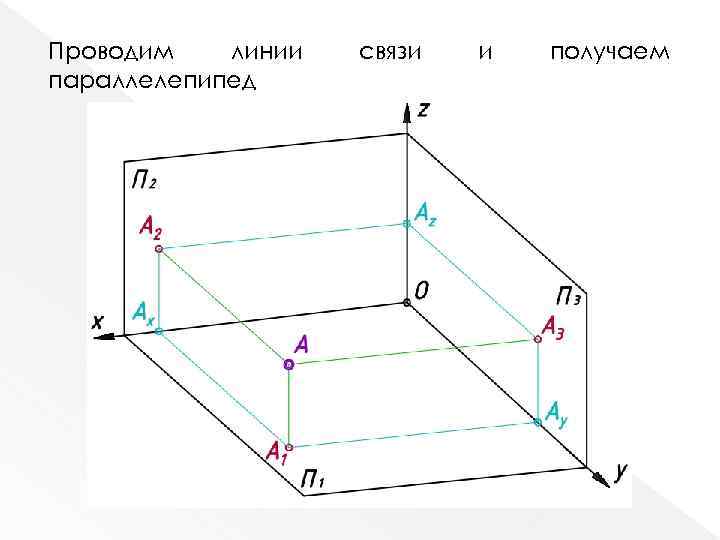Проводим линии параллелепипед связи и получаем

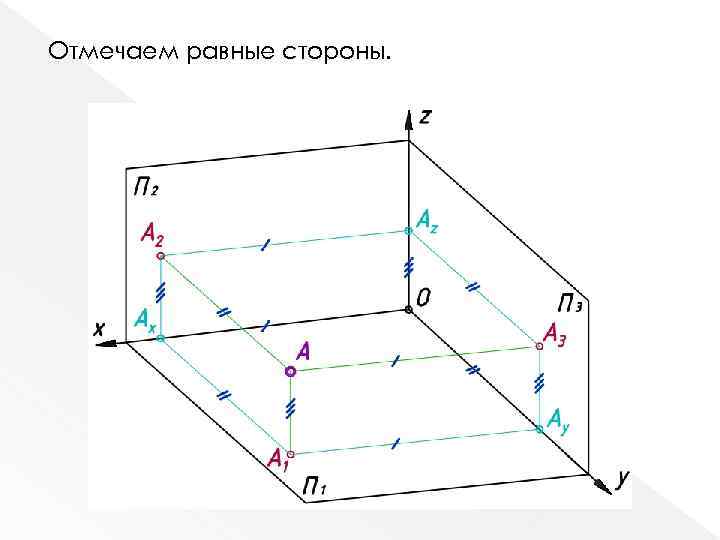Отмечаем равные стороны.

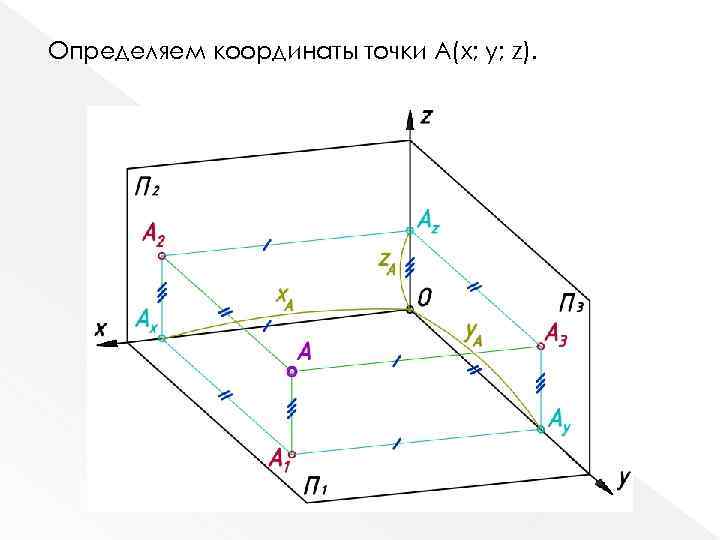Определяем координаты точки А(x; y; z).

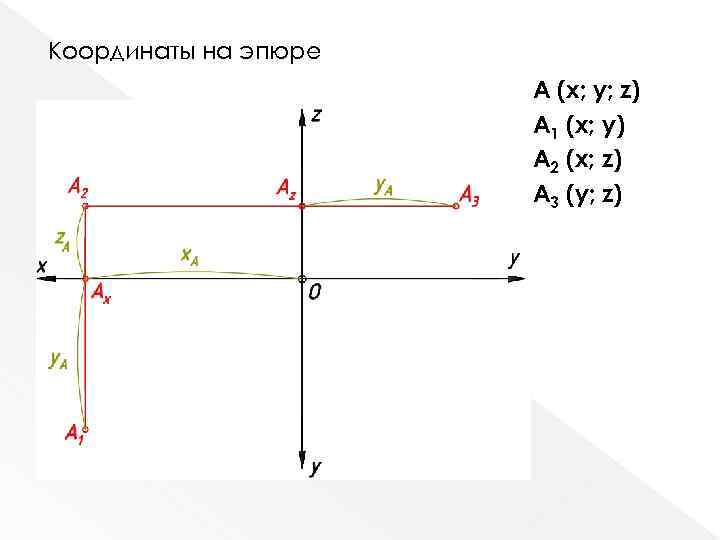Координаты на эпюре A (x; y; z) A 1 (x; y) A 2 (x; z) A 3 (y; z)

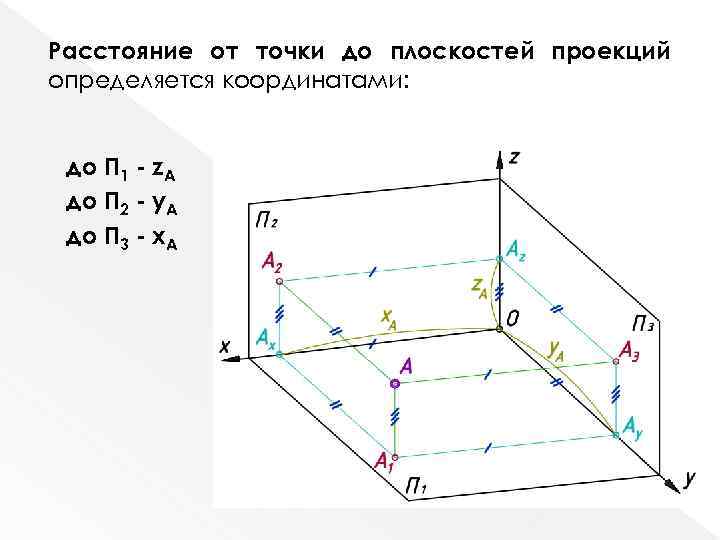Расстояние от точки до плоскостей проекций определяется координатами: до П 1 - z. А до П 2 - y. А до П 3 - x. А

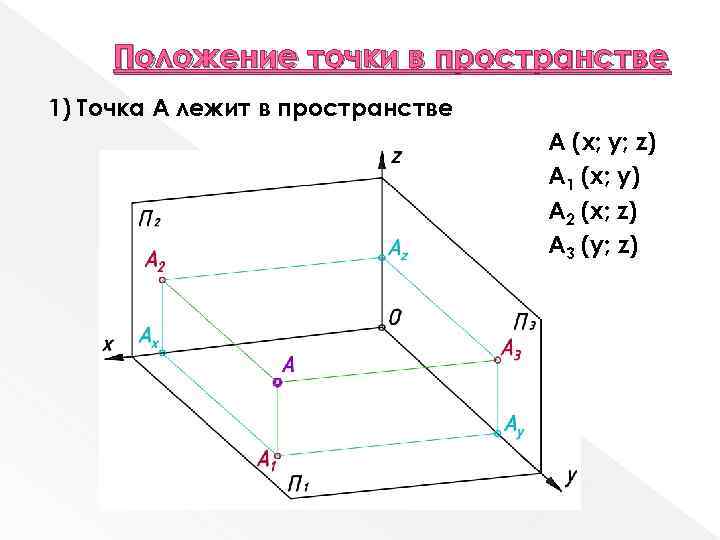Положение точки в пространстве 1) Точка А лежит в пространстве A (x; y; z) A 1 (x; y) A 2 (x; z) A 3 (y; z)

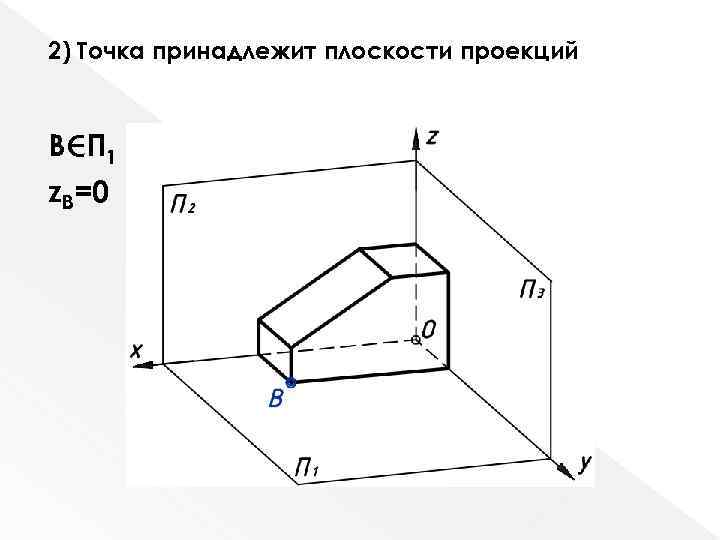2) Точка принадлежит плоскости проекций В П 1 z. B=0

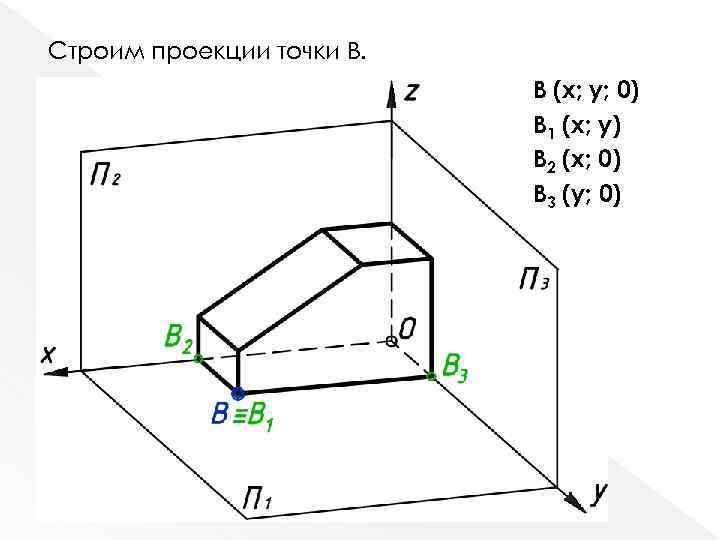Строим проекции точки В. В (x; y; 0) В 1 (x; y) В 2 (x; 0) В 3 (y; 0)

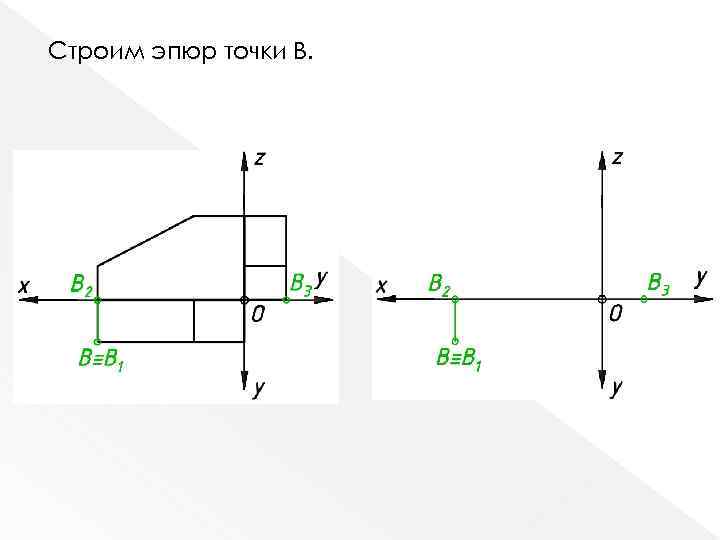Строим эпюр точки В.

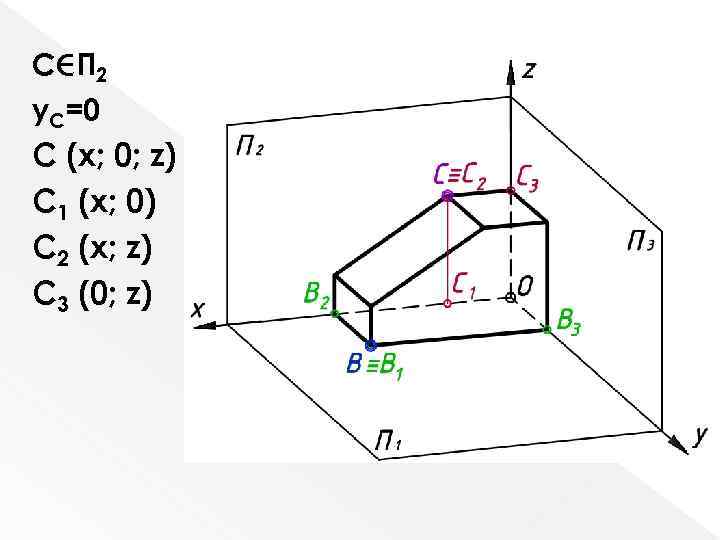С П 2 y. C=0 С (x; 0; z) С 1 (x; 0) С 2 (x; z) С 3 (0; z)

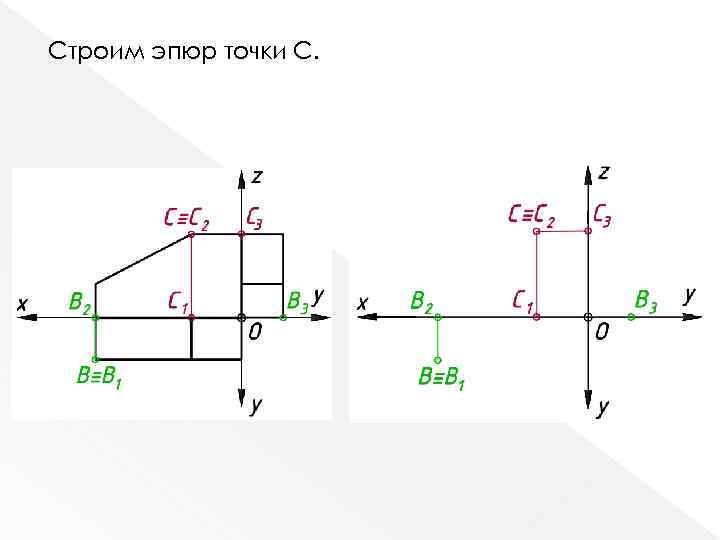Строим эпюр точки С.

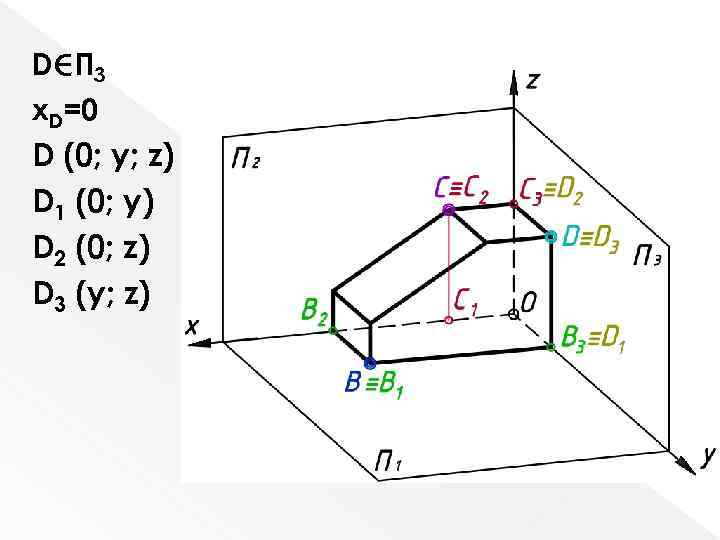D П 3 x. D=0 D (0; y; z) D 1 (0; y) D 2 (0; z) D 3 (y; z)

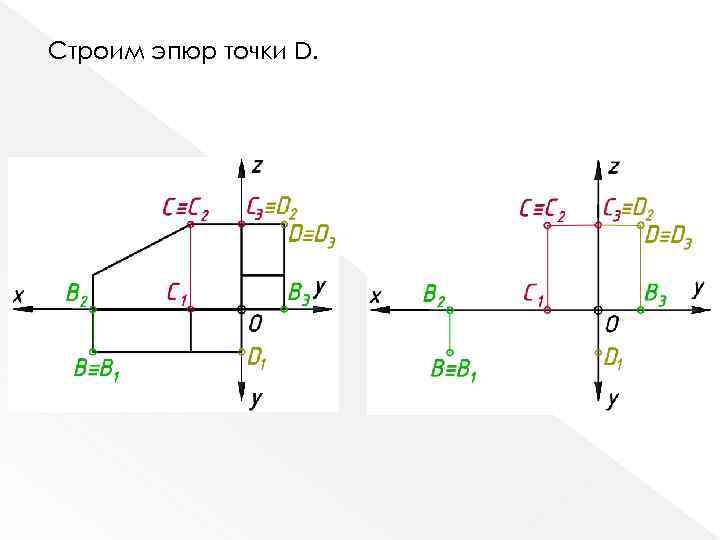Строим эпюр точки D.

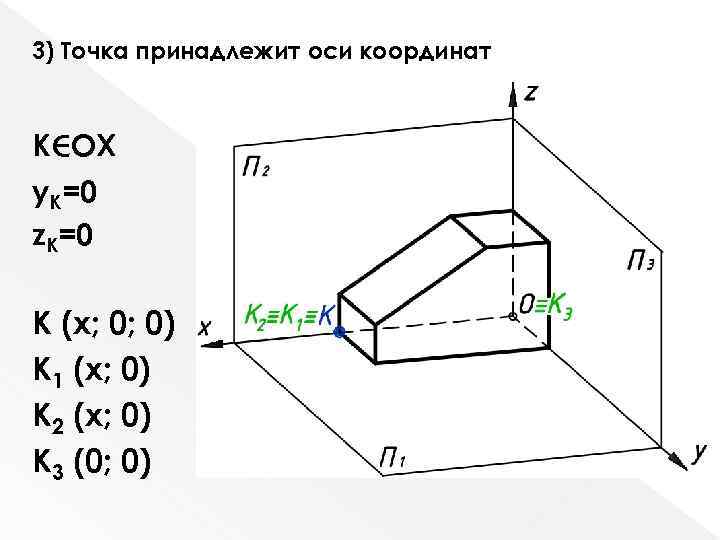3) Точка принадлежит оси координат K OX y. K=0 z. K=0 K (x; 0; 0) K 1 (x; 0) K 2 (x; 0) K 3 (0; 0)

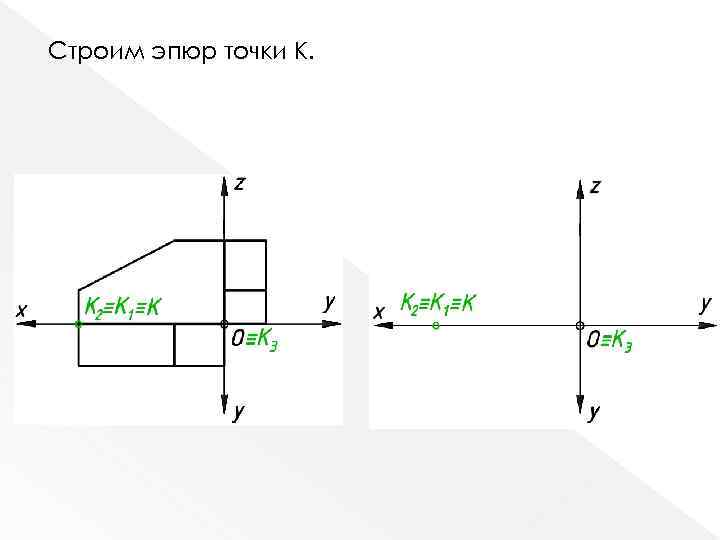Строим эпюр точки K.

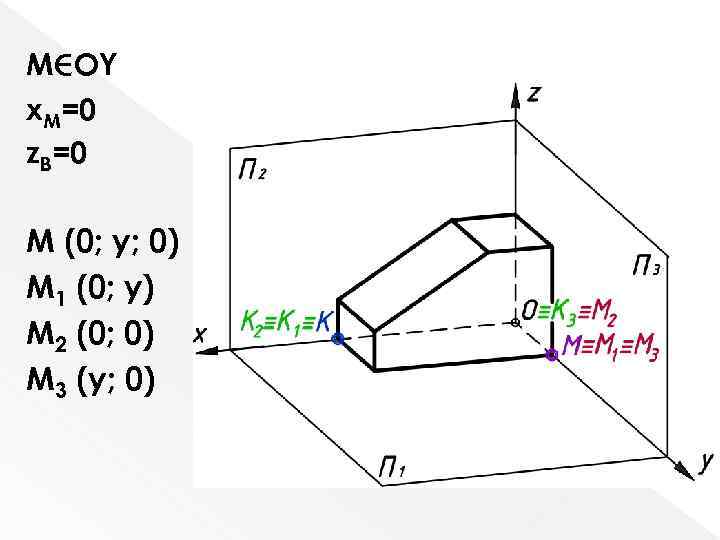M OY x. M=0 z. B=0 M (0; y; 0) M 1 (0; y) M 2 (0; 0) M 3 (y; 0)

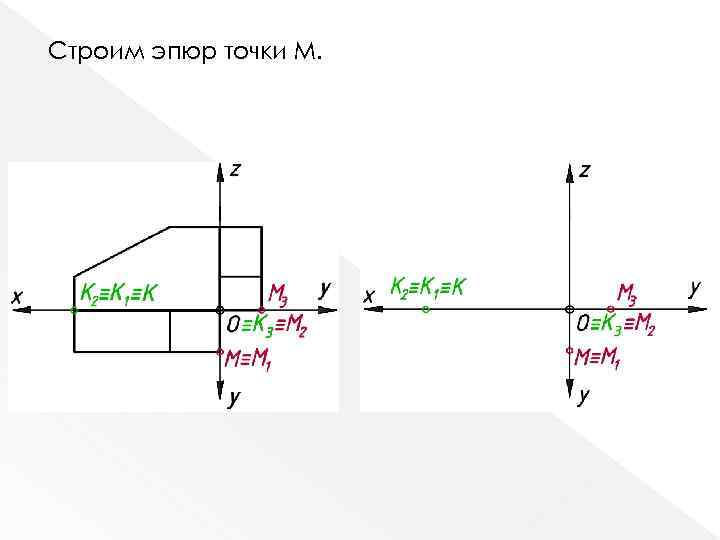Строим эпюр точки M.

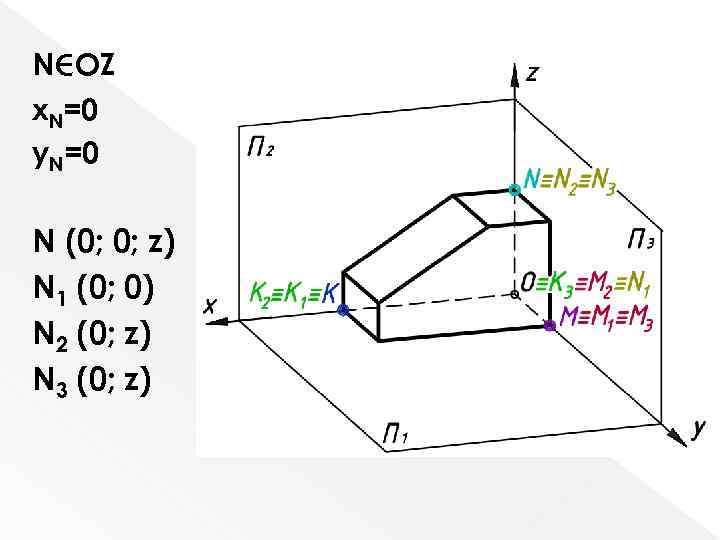N OZ x. N=0 y. N=0 N (0; 0; z) N 1 (0; 0) N 2 (0; z) N 3 (0; z)

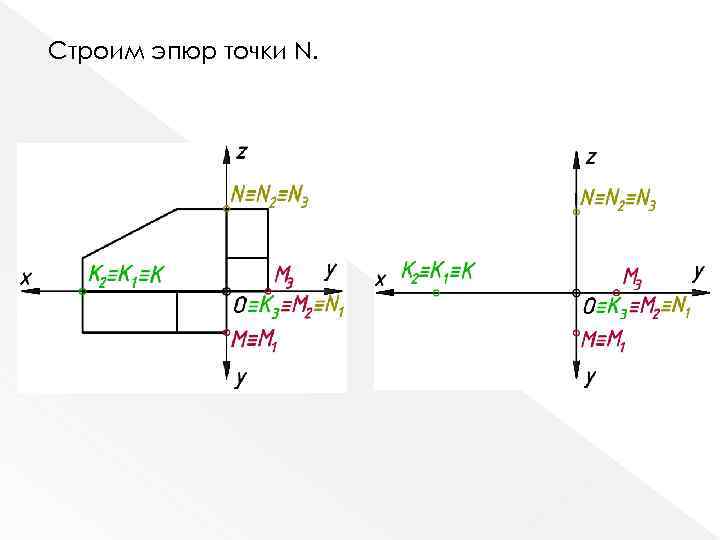Строим эпюр точки N.