Лекция 2 Теория функций нескольких переменных ТФНП 1

Лекция 2 Теория функций нескольких переменных (ТФНП) 1. Дифференциалы высших порядков 2. Геометрические приложения ТФНП 3. Экстремумы ФНП 4. Условные экстремумы ФНП 5. Отыскание наибольшего и наименьшего значений ФНП 1

1. Дифференциалы высших порядков Дифференциал функции двух переменных – функция переменных 2

При фиксированных для также можно поставить вопрос о дифференциале первого порядка, тогда для исходной функции u возникает понятие второго дифференциала и т. д. – дифференциал второго порядка – дифференциал третьего порядка 3

Найдем формулу для вычисления дифференциала второго порядка. 4

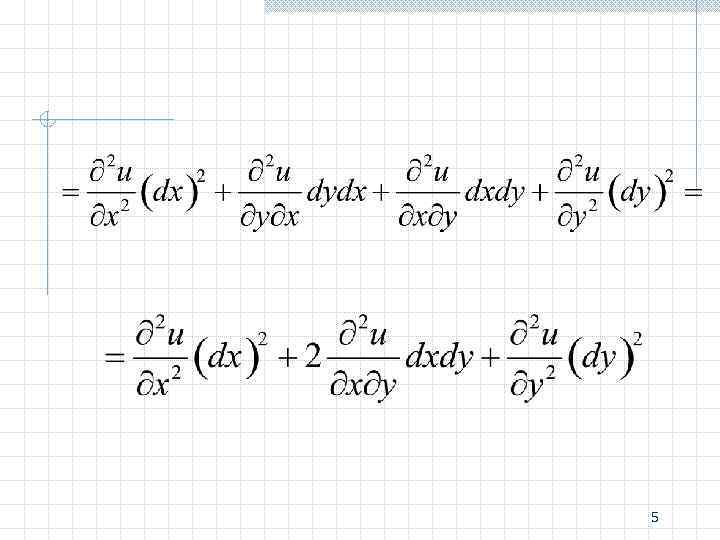5

2. Геометрические приложения ТФНП Определение. Прямая линия называется касательной к поверхности в некоторой точке P 0(x 0, y 0, z 0), если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку Р 0 6

Рассмотрим поверхность Q: Определение. Если в точке или хотя бы одна из производных не существует, то точка М называется особой точкой поверхности Q. Определение. Если в точке всечастные производные существуют, непрерывны, и хотя бы одна из них отлична от нуля, то точка М называется обыкновенной точкой 7 поверхности Q.

2. Геометрические приложения ТФНП Определение. Плоскость, в которой расположены все касательные к поверхности в точке Р 0 называется касательной плоскостью к поверхности в точке Р 0. Теорема. Все касательные прямые к данной поверхности в ее обыкновенной точке лежат в одной плоскости. 8

Теорема (о существовании касательной плоскости) Если Р 0 – обыкновенная точка плоскости Q, то через точку Р 0 можно провести касательную плоскость Доказательство. Проведем через точку Р 0 произвольную линию – вектор-функция Вектор, направленный по касательной к линии L: 9

Подставим координаты поверхности: в уравнение (получим верное равенство) Дифференцируем по t: - справедливо для любой точки линии L ( в частности для фиксированной точки ) 10

где перпендикулярен касательной к L в точке L выбирали произвольным образом перпендикулярен всем касательным нормальный вектор касательной к поверхности Q в точке плоскости 11

Определение. Нормалью к поверхности Q в точке называется прямая, проходящая через точку перпендикулярно плоскости касательной для Q в точке 12

Рассмотрим поверхность Q: нормальный вектор поверхности Q в т. Р 0. Уравнение касательной плоскости Уравнение нормали 13

3. Экстремум ФНП Определение. Точка называется точкой локального максимума или минимума функции если в δ-окрестности этой точки функция непрерывна и удовлетворяет неравенству или Определение. Локальные максимумы и минимумы функции u= f(P) называют локальными экстремумами. 14

Теорема (необходимое условие существования экстремума) Если 1. Р 0 – точка экстремума, 2. f(P) – дифференцируемая в точке Р 0 функция двух переменных, то частные производные первого порядка в этой точке равны нулю 15

Следствие 1 Если P 0 – стационарная точка функции u ( частные производные первого порядка равны нулю), то Следствие 2 Точки возможного экстремума: а) стационарные точки, б) точки , в которых функция u=f(P) не дифференцируема. 16

Теорема (достаточное условие экстремума) Если 1. Р 0 – стационарная точка для u = f(P), 2. u – дважды дифференцируемая функция в окрестности точки Р 0 , 3. вторые производные функции u непрерывны в точке Р 0 , 17

то 1. если (сохраняет знак «-» ), то P 0 - точка максимума, 2. если (сохраняет знак «+» ), то P 0 - точка минимума, 3. если не сохраняет знака при изменении знака dxi, то в точке P 0 нет экстремума, 4. если и равенство нулю возникает в случае, когда не все то для точки P 0 требуется дополнительное 18 исследование.

4. Условные экстремумы На практике часто встречаются задачи об отыскании экстремумов функции, аргументы которой не являются независимыми переменными, а удовлетворяют определенным условиям связи (уравнениям). Такие экстремумы называются условными. 19

Постановка задачи: Пусть 1. u=f(P), 2. - уравнение связи Найти условные экстремумы функции u. Поставленная задача сводится к задаче отыскания обычного экстремума методом Лагранжа. 20

Определение. Функцией Лагранжа, соответствующей данной функции и условию связи называется функция вида где множитель Лагранжа. 21

Теорема Точке обычного экстремума функции соответствует точка условного экстремума непрерывной функции u(P) при условии связи 22

Общая схема отыскания условного экстремума 1. Поиск стационарных точек функции Лагранжа (необходимое условие экстремума). - система уравнений для отыскания стационарных точек 23

2. Определение типа экстремума (достаточное условие экстремума). Для установления факта наличия экстремума и определения типа экстремума нужно исследовать знак При этом нужно учитывать, что зависят друг от друга из-за условий связи. 24

Пример На плоскости OXY дана фигура, ограниченная линиями Найдите размеры прямоугольника две стороны которого совпадают, а две другие параллельны осям координат, если одна из его вершин M(x, y) находится на параболе, а прямоугольник вписан в эту фигуру так, чтобы площадь прямоугольника была наибольшей. 25

Площадь прямоугольника: Точка M принадлежит параболе уравнение связи: 26

Функция Лагранжа 1. Найдем стационарные точки функции Лагранжа. 27

2. Установим тип экстремума. Вычислим частные производные Из уравнения связи следует связь дифференциалов При 28

условный максимум функции S, 29

5. Отыскание наибольшего и наименьшего значений ФНП Теорема Если функция u=f(P) дифференцируема в ограниченной замкнутой области, то она достигает наибольшего M (наименьшего m) значений или в стационарной точке, или в граничной точке области. 30

Схема поиска наибольшего (наименьшего) значения 1. Найти стационарные точки P 0 и вычислить 2. Найти m. Г и M Г наименьшее и наибольшее значения u=f(P) на границе области 3. Выбрать 31

Пример u - дифференцируема D - замкнутая, ограничена Уравнение границы 1. Стационарные точки 32

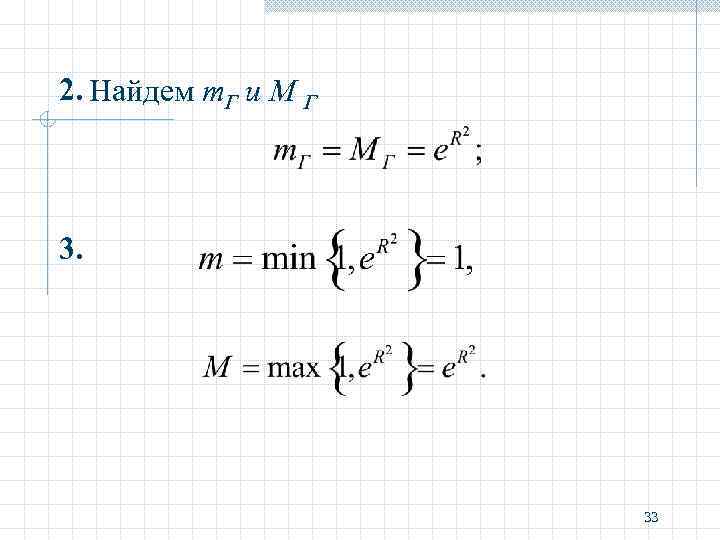2. Найдем m. Г и M Г 3. 33