Лекция № 2 Солодухин Е. А.

Лекция № 2 Солодухин Е. А. 1

Содержание лекции • Ортогональная система двух плоскостей проекций. • Метод Монжа. • Ортогональная система трех плоскостей проекций. • Проецирование точки в системе двух плоскостей проекций. • Проецирование точки в системе трех плоскостей проекций. 2

Ортогональная система двух плоскостей проекций 3

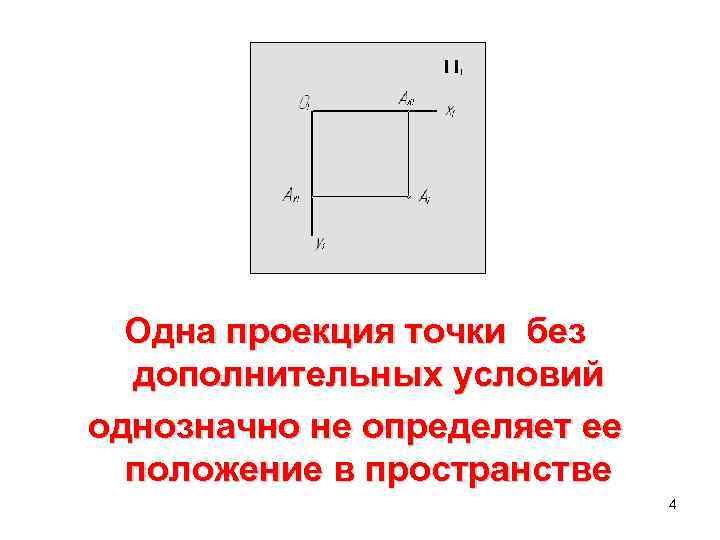
Одна проекция точки без дополнительных условий однозначно не определяет ее положение в пространстве 4

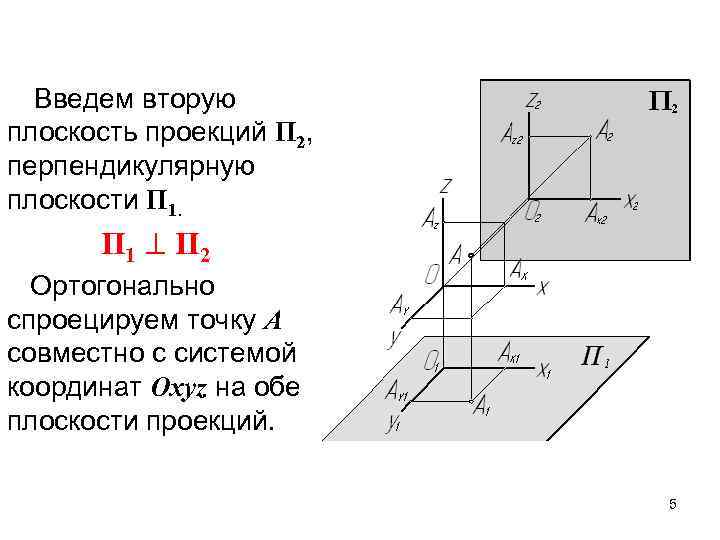
Введем вторую плоскость проекций П 2, перпендикулярную плоскости П 1 П 2 Ортогонально спроецируем точку А совместно с системой координат Oxyz на обе плоскости проекций. 5

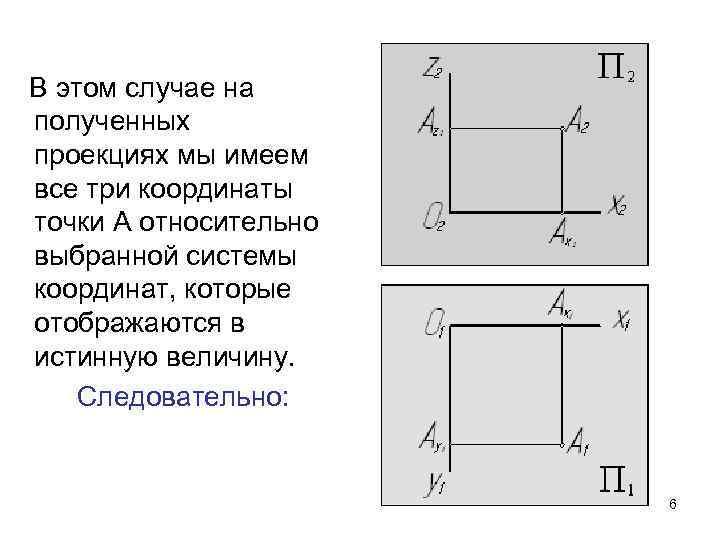
В этом случае на полученных проекциях мы имеем все три координаты точки А относительно выбранной системы координат, которые отображаются в истинную величину. Следовательно: 6

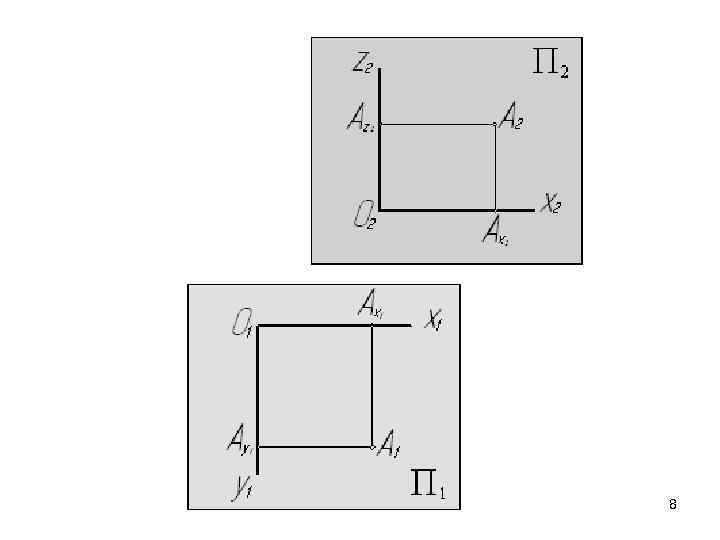
Ортогональные проекции точки на две взаимно перпендикулярные плоскости однозначно определяют положение точки в пространстве и делают изображения обратимыми. 7

8

Метод Монжа. 9

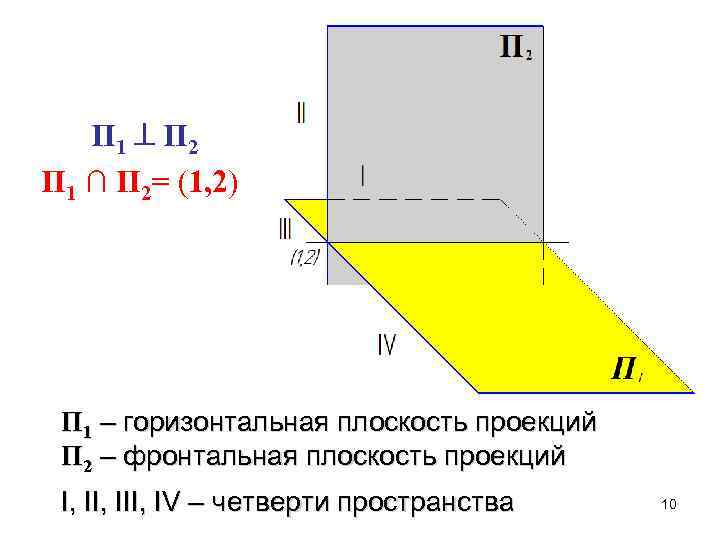
П 1 П 2 П 1 ∩ П 2= (1, 2) П 1 – горизонтальная плоскость проекций П 2 – фронтальная плоскость проекций I, III, IV – четверти пространства 10

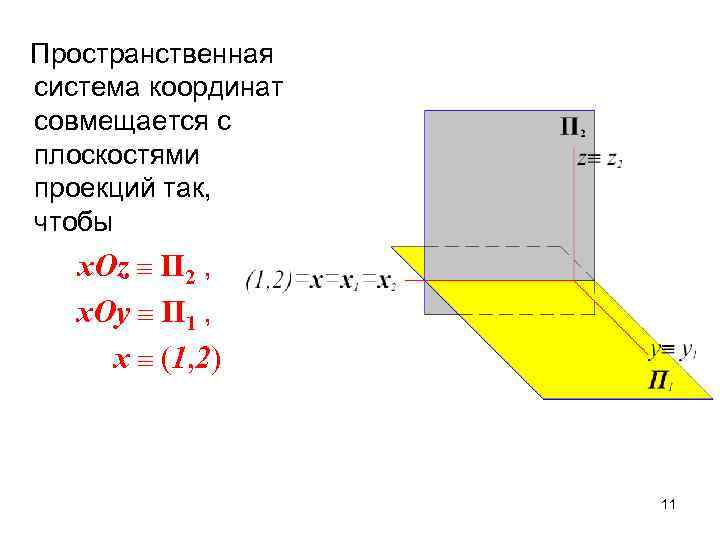
Пространственная система координат совмещается с плоскостями проекций так, чтобы x. Oz П 2 , x. Oy П 1 , x (1, 2) 11

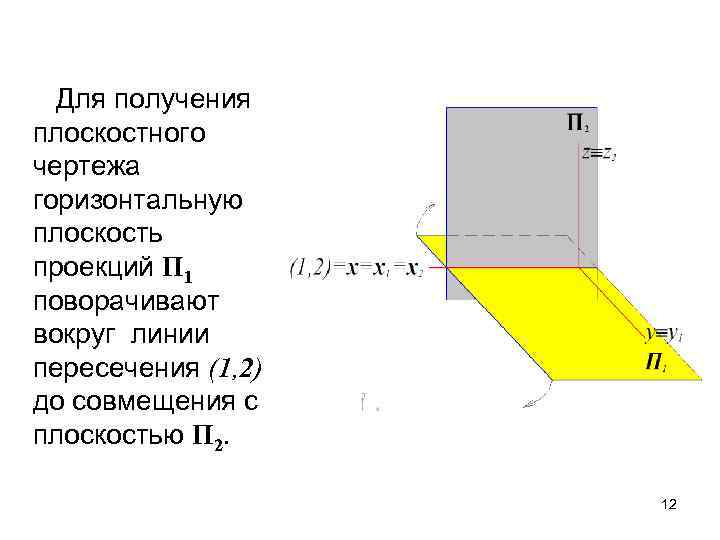
Для получения плоскостного чертежа горизонтальную плоскость проекций П 1 поворачивают вокруг линии пересечения (1, 2) до совмещения с плоскостью П 2. 12

13

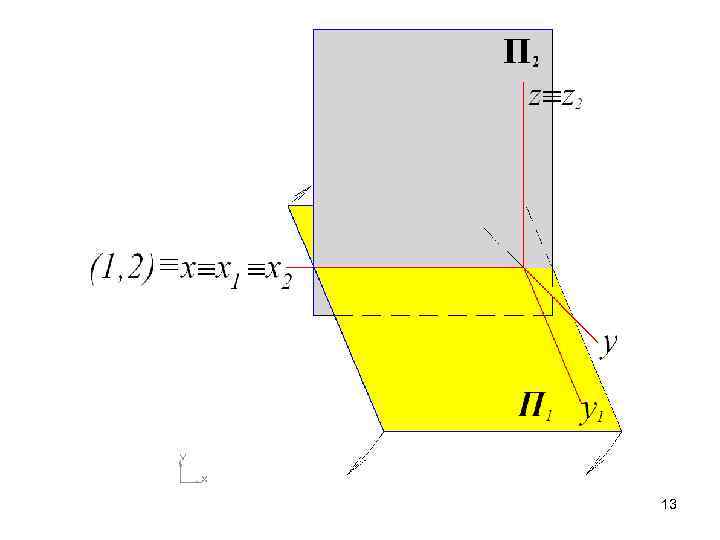
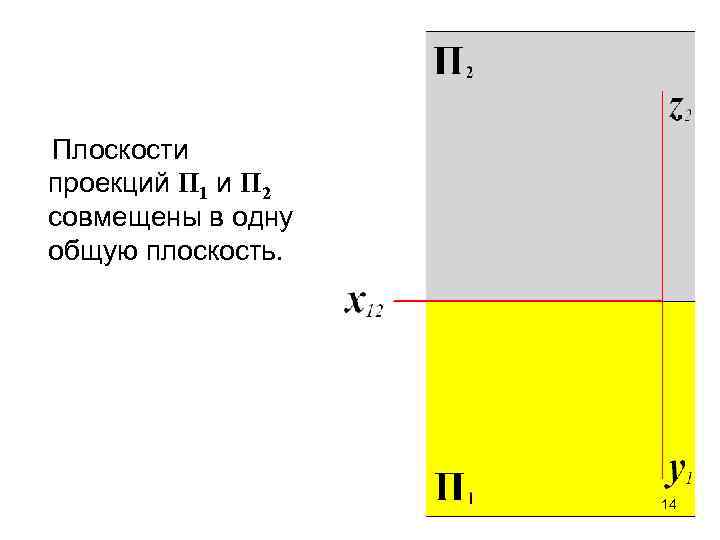
Плоскости проекций П 1 и П 2 совмещены в одну общую плоскость. 14

Так как плоскости проекций бесконечны, то их границы не показывают. Координатные оси y и z также не показывают. В дальнейшем, когда не требуется знать положение объекта в пространстве относительно системы координат Oxyz, ось х1, 2 также может не изображаться. 15

Ортогональная система трех плоскостей проекций 16

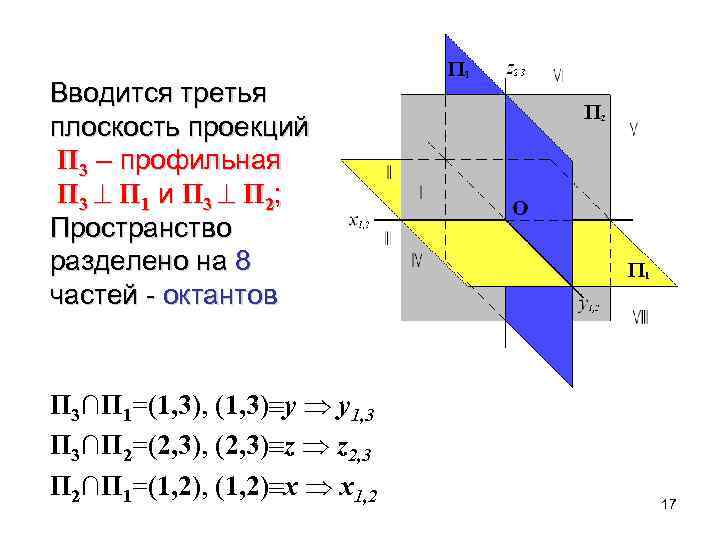
Вводится третья плоскость проекций П 3 – профильная П 3 П 1 и П 3 П 2; Пространство разделено на 8 частей - октантов П 3∩П 1=(1, 3), (1, 3) y y 1, 3 П 3∩П 2=(2, 3), (2, 3) z z 2, 3 П 2∩П 1=(1, 2), (1, 2) x x 1, 2 17

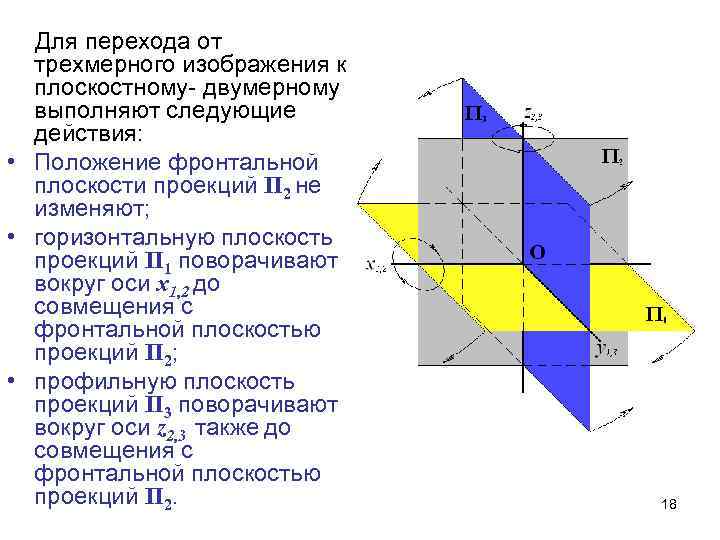
Для перехода от трехмерного изображения к плоскостному- двумерному выполняют следующие действия: • Положение фронтальной плоскости проекций П 2 не изменяют; • горизонтальную плоскость проекций П 1 поворачивают вокруг оси x 1, 2 до совмещения с фронтальной плоскостью проекций П 2; • профильную плоскость проекций П 3 поворачивают вокруг оси z 2, 3 также до совмещения с фронтальной плоскостью проекций П 2. 18

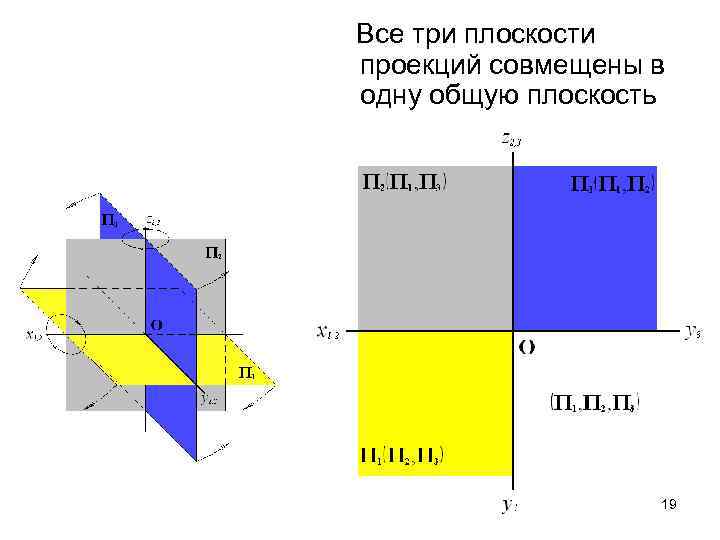
Все три плоскости проекций совмещены в одну общую плоскость 19

Проецирование точки 20

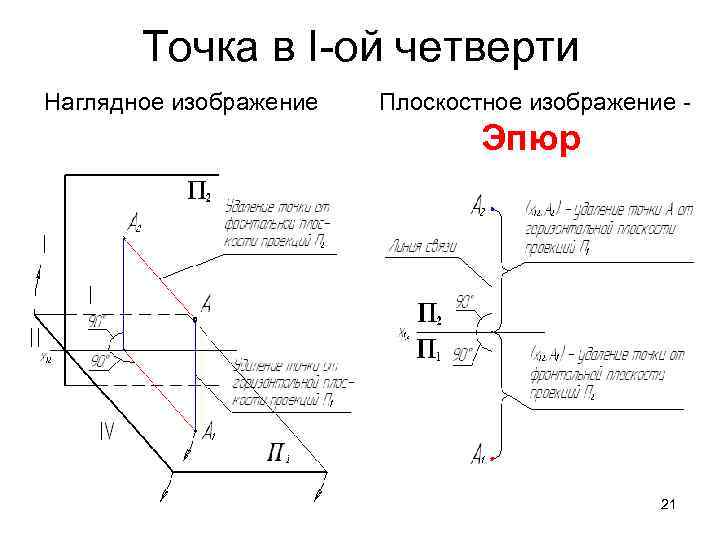
Точка в I-ой четверти Наглядное изображение Плоскостное изображение - Эпюр 21

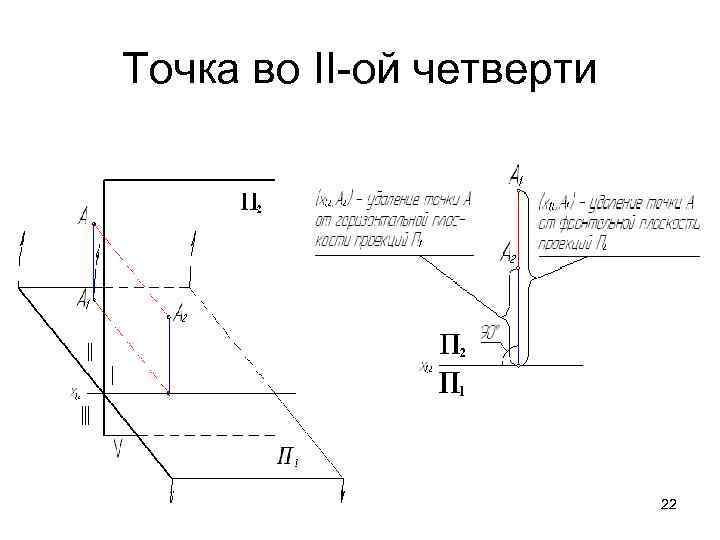
Точка во II-ой четверти 22

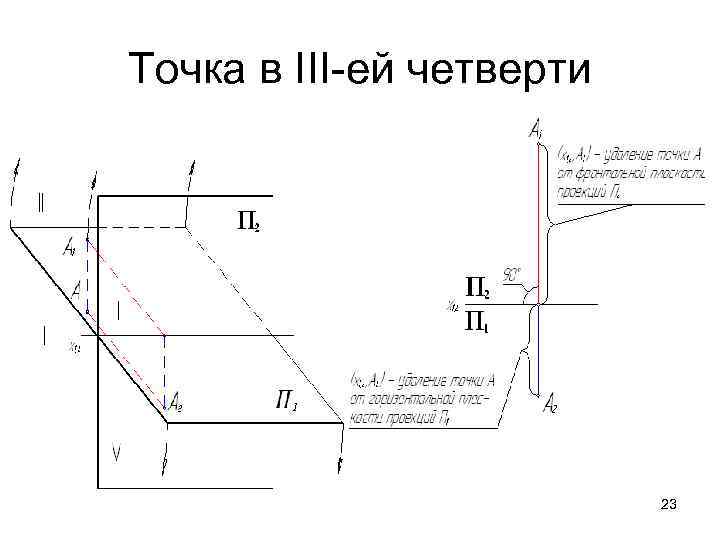
Точка в III-ей четверти 23

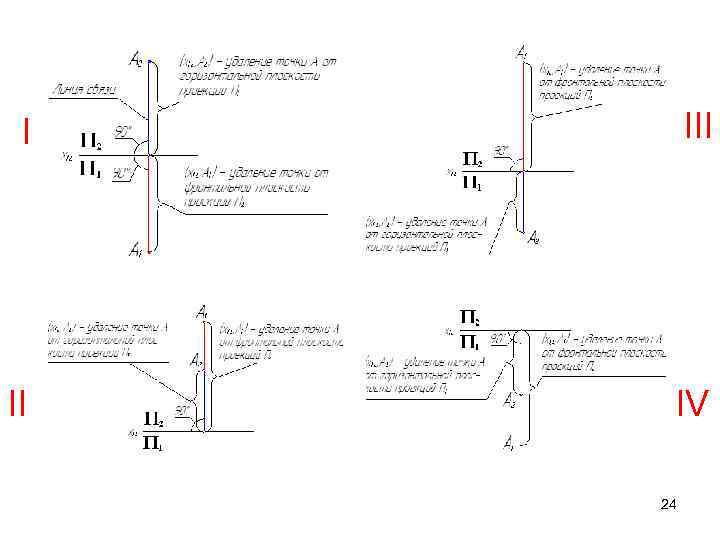
I III II IV 24

Горизонтальная и фронтальная проекции точки располагаются на одной прямой, перпендикулярной оси x 1, 2 А 1 А 2 х1, 2 Расстояние от оси x 1, 2 до горизонтальной проекции точки определяет расстояние от самой точки до фронтальной плоскости проекций. (х1, 2 , А 1) = (А, П 2) - глубина Расстояние от оси x 1, 2 до фронтальной проекции точки определяет расстояние от самой точки до горизонтальной плоскости проекций. (х1, 2 , А 2) = (А, П 1) - высота 25

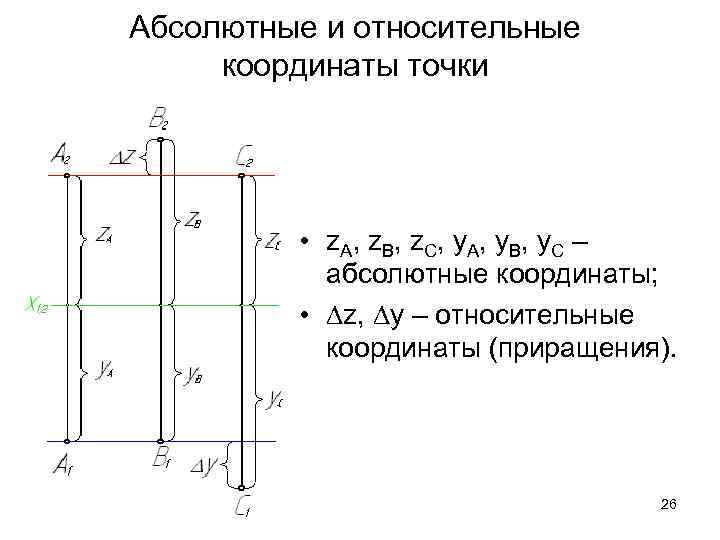
Абсолютные и относительные координаты точки • z. A, z. B, z. C, y. A, y. B, y. C – абсолютные координаты; • z, y – относительные координаты (приращения). 26

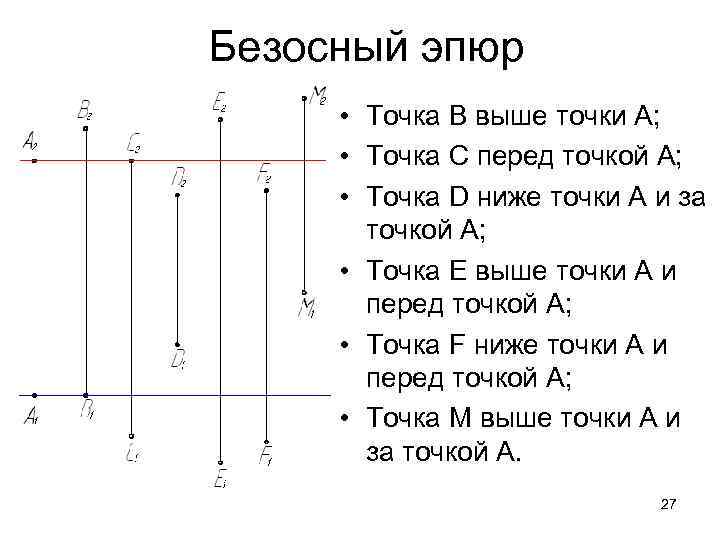
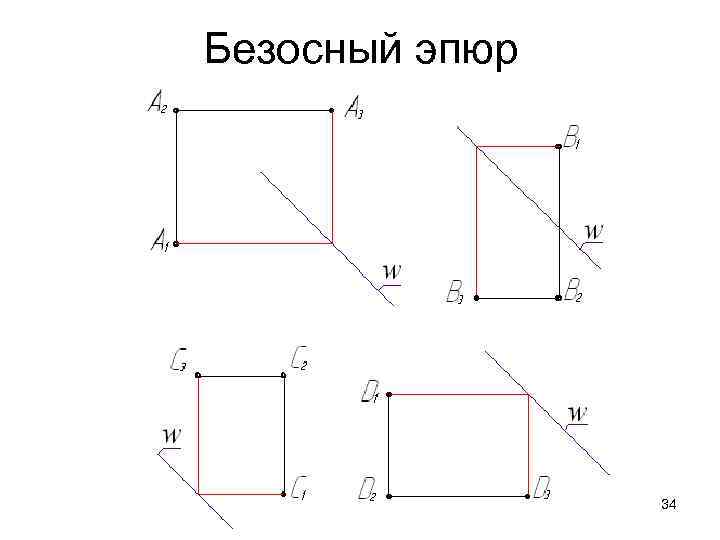
Безосный эпюр • Точка В выше точки А; • Точка С перед точкой А; • Точка D ниже точки А и за точкой А; • Точка Е выше точки А и перед точкой А; • Точка F ниже точки А и перед точкой А; • Точка М выше точки А и за точкой А. 27

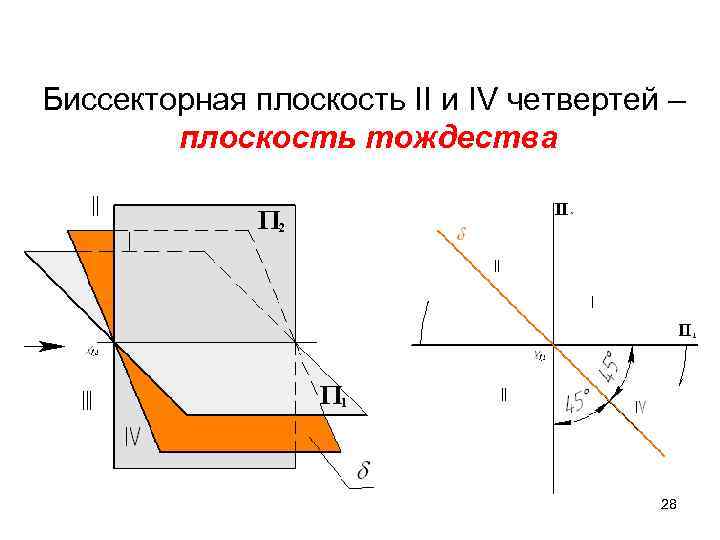
Биссекторная плоскость II и IV четвертей – плоскость тождества 28

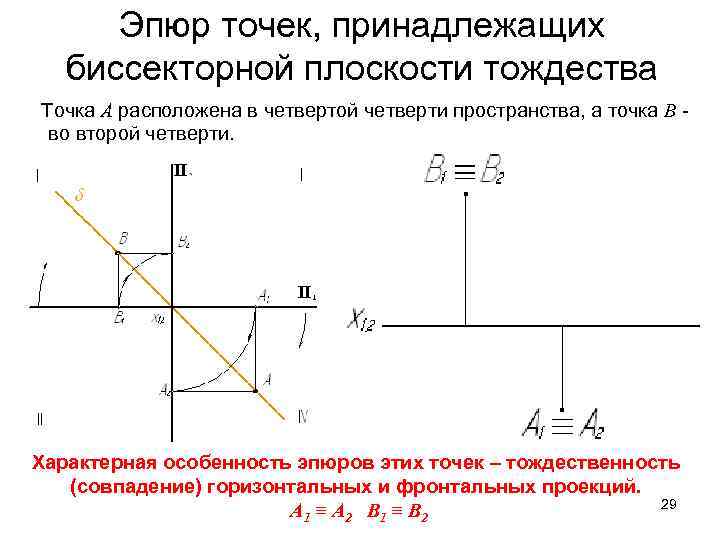
Эпюр точек, принадлежащих биссекторной плоскости тождества Точка А расположена в четвертой четверти пространства, а точка В - во второй четверти. Характерная особенность эпюров этих точек – тождественность (совпадение) горизонтальных и фронтальных проекций. 29 А 1 ≡ А 2 В 1 ≡ В 2

Проецирование точки в системе трех ортогональных плоскостей проекций 30

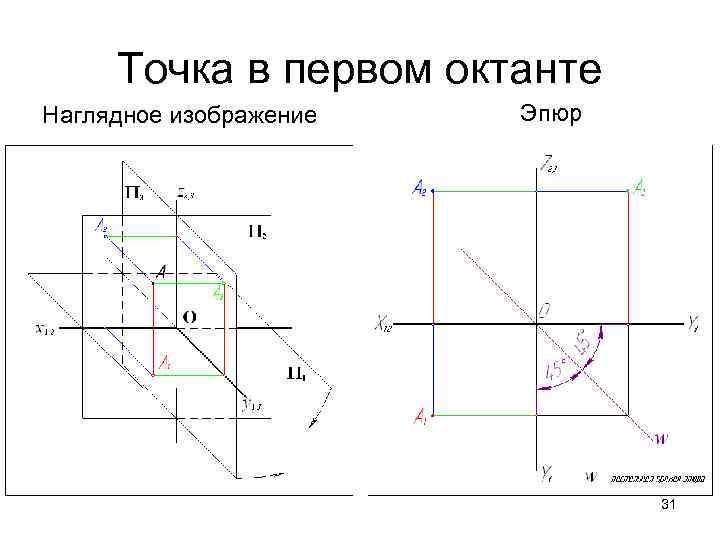
Точка в первом октанте Наглядное изображение Эпюр 31

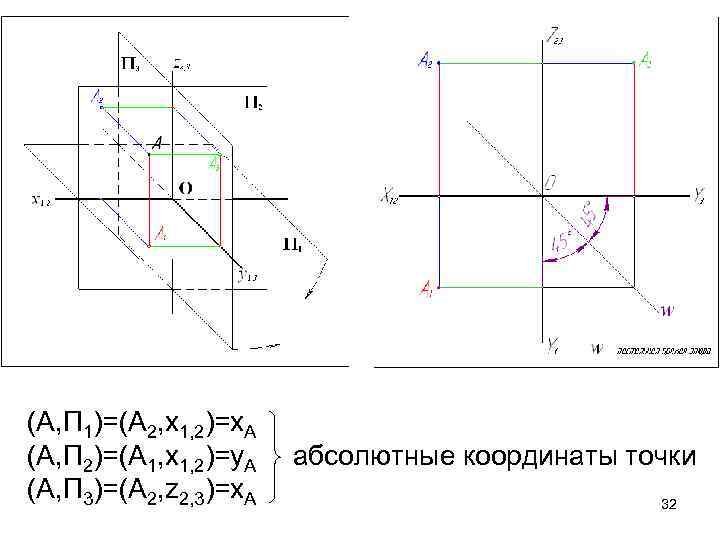
(A, П 1)=(А 2, х1, 2)=х. А (A, П 2)=(А 1, х1, 2)=y. А абсолютные координаты точки (A, П 3)=(А 2, z 2, 3)=х. А 32

Условия, которым должен удовлетворять эпюр точки, расположенной в любой части пространства, в системе трех ортогональных плоскостей проекций: • А 1 А 2 х1, 2 • А 2 А 3 z 2, 3 • (A 1, x 1, 2) = (A 3, z 2, 3) 33

Безосный эпюр 34