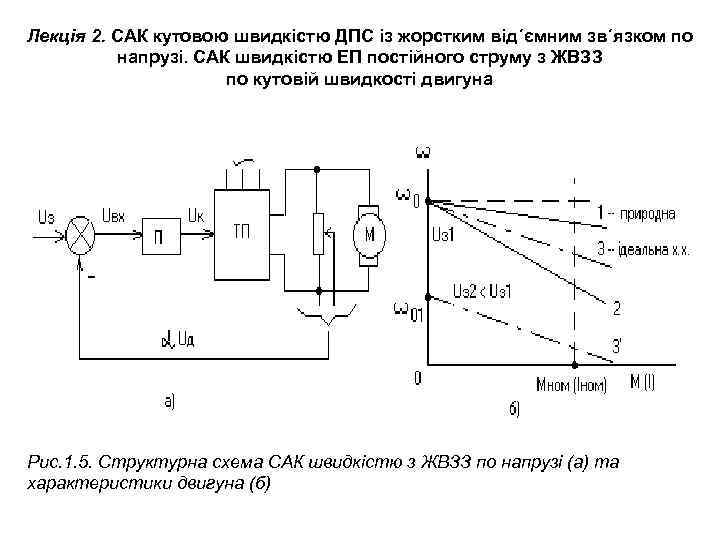
 Лекція 2. САК кутовою швидкістю ДПС із жорстким від΄ємним зв΄язком по напрузі. САК швидкістю ЕП постійного струму з ЖВЗЗ по кутовій швидкості двигуна Рис. 1. 5. Структурна схема САК швидкістю з ЖВЗЗ по напрузі (а) та характеристики двигуна (б)
Лекція 2. САК кутовою швидкістю ДПС із жорстким від΄ємним зв΄язком по напрузі. САК швидкістю ЕП постійного струму з ЖВЗЗ по кутовій швидкості двигуна Рис. 1. 5. Структурна схема САК швидкістю з ЖВЗЗ по напрузі (а) та характеристики двигуна (б)
 Система рівнянь у сталому режимі всіх елементів має вигляд ( 1. 11) де кп = Uу / Uвх; кп = Етп / Uк – відповідно коефіцієнти підсилення підсилювача П та тиристорного перетворювача ТП; Етп, Ед – відповідно ЕРС перетворювача ТП і двигуна М; Rтп, Rд – опори перетворювача і двигуна; α = Uзз / Uд – коефіцієнт підсилення ЗЗ по напрузі.
Система рівнянь у сталому режимі всіх елементів має вигляд ( 1. 11) де кп = Uу / Uвх; кп = Етп / Uк – відповідно коефіцієнти підсилення підсилювача П та тиристорного перетворювача ТП; Етп, Ед – відповідно ЕРС перетворювача ТП і двигуна М; Rтп, Rд – опори перетворювача і двигуна; α = Uзз / Uд – коефіцієнт підсилення ЗЗ по напрузі.
 Після перетворювань одержимо рівняння для механічної характеристики в замкненій системі: ( 1. 12) ( 1. 13) чи де кс = ктп·кп. Якщо вважати, що коефіцієнти кп і ктп постійні, то ( 1. 13) є рівнянням прямої. Перший член рівняння визначає кутову швидкість ідеального х. х. , пропорційну напрузі Uз (характеристики 3 і 3΄ на рис. 1. 5, б). Аналіз (1. 13) показує, що при коефіцієнті підсилення системи кс = ктп·кп→∞ жорсткість механічної характеристики в системі, що розглядається, не перевершує жорсткості природної характеристики двигуна (характеристика 1 на рис. 1. 5, б), підключеного до мережі з постійною напругою Uд = с·ω0. Таким чином, у такій системі найбільший діапазон регулювання буде залежати від падіння напруги в якірному ланцюзі двигуна.
Після перетворювань одержимо рівняння для механічної характеристики в замкненій системі: ( 1. 12) ( 1. 13) чи де кс = ктп·кп. Якщо вважати, що коефіцієнти кп і ктп постійні, то ( 1. 13) є рівнянням прямої. Перший член рівняння визначає кутову швидкість ідеального х. х. , пропорційну напрузі Uз (характеристики 3 і 3΄ на рис. 1. 5, б). Аналіз (1. 13) показує, що при коефіцієнті підсилення системи кс = ктп·кп→∞ жорсткість механічної характеристики в системі, що розглядається, не перевершує жорсткості природної характеристики двигуна (характеристика 1 на рис. 1. 5, б), підключеного до мережі з постійною напругою Uд = с·ω0. Таким чином, у такій системі найбільший діапазон регулювання буде залежати від падіння напруги в якірному ланцюзі двигуна.
 Статизм у замкненій систтемі керування при навантаженні, рівному Мном, може бути визначений як відношення перепаду кутової швидкості за рівнянням (1. 13) до дійсного значення кутової швидкості ідеального х. х. : ( 1. 14) де Rя = Rтп + RД. Аналіз (1. 14) показує наступне: При кінцевому значенні коефіцієнта підсилення 0 < кс < ∞ статизм системи буде збільшуватись при зменшенні задавальної напруги; Мінімальний перепад швидкості (при кс → ∞) зумовлюється внутрішнім опором якоря двигуна, тобто гранична жорсткість характеристики визначається жорсткістю природної характеристики, а відносна жорсткість падає по мірі зниження задавальної напруги. Тому така САК не може забезпечити великий діапазон регулювання і не дозволяє з високою точністю підтримувати швидкість.
Статизм у замкненій систтемі керування при навантаженні, рівному Мном, може бути визначений як відношення перепаду кутової швидкості за рівнянням (1. 13) до дійсного значення кутової швидкості ідеального х. х. : ( 1. 14) де Rя = Rтп + RД. Аналіз (1. 14) показує наступне: При кінцевому значенні коефіцієнта підсилення 0 < кс < ∞ статизм системи буде збільшуватись при зменшенні задавальної напруги; Мінімальний перепад швидкості (при кс → ∞) зумовлюється внутрішнім опором якоря двигуна, тобто гранична жорсткість характеристики визначається жорсткістю природної характеристики, а відносна жорсткість падає по мірі зниження задавальної напруги. Тому така САК не може забезпечити великий діапазон регулювання і не дозволяє з високою точністю підтримувати швидкість.
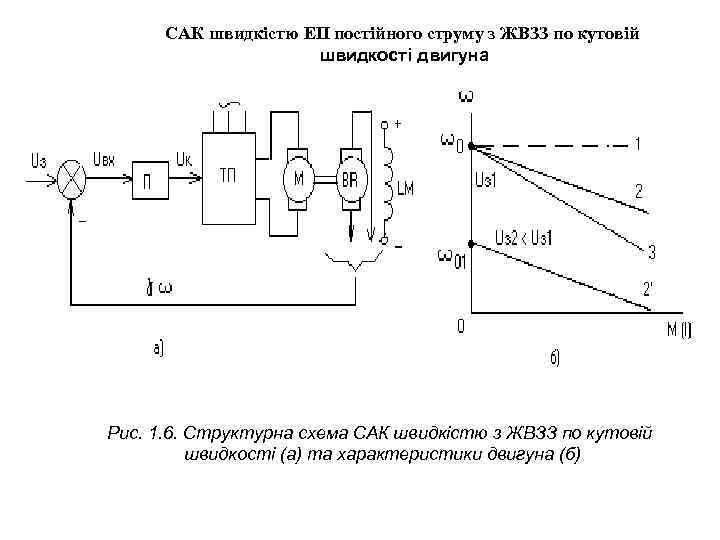 САК швидкістю ЕП постійного струму з ЖВЗЗ по кутовій швидкості двигуна Рис. 1. 6. Структурна схема САК швидкістю з ЖВЗЗ по кутовій швидкості (а) та характеристики двигуна (б)
САК швидкістю ЕП постійного струму з ЖВЗЗ по кутовій швидкості двигуна Рис. 1. 6. Структурна схема САК швидкістю з ЖВЗЗ по кутовій швидкості (а) та характеристики двигуна (б)
 Принцип дії жорсткого ЗЗ по кутовій швидкості (рис. 1. 6) полягає в наступному: зі збільшенням навантаження на валу двигуна зменшується його кутова швидкість та знижується сигнал із тахогенератора BR, який знаходиться на одному валу з двигуном М; напруга, яка знімається із якоря тахогенератора, пропорційна кутовій швидкості двигуна. Оскільки задавальний сигнал залишається при цьому постійним, то сигнал на вході підсилювача П при зниженні кутової швидкості збільшується, отже, збільшується ЕРС перетворювача ТП, що автоматично призводить до компенсації зниження кутової швидкості привода. Система рівнянь для даної схеми має вигляд ( 1. 15)
Принцип дії жорсткого ЗЗ по кутовій швидкості (рис. 1. 6) полягає в наступному: зі збільшенням навантаження на валу двигуна зменшується його кутова швидкість та знижується сигнал із тахогенератора BR, який знаходиться на одному валу з двигуном М; напруга, яка знімається із якоря тахогенератора, пропорційна кутовій швидкості двигуна. Оскільки задавальний сигнал залишається при цьому постійним, то сигнал на вході підсилювача П при зниженні кутової швидкості збільшується, отже, збільшується ЕРС перетворювача ТП, що автоматично призводить до компенсації зниження кутової швидкості привода. Система рівнянь для даної схеми має вигляд ( 1. 15)
 де Uзс – задавальна напруга в системі з ЗЗ по ω; γ = Uзз / ω – коефіцієнт передачі ЗЗ по ω. Усі інші позначення ті самі, що і для розглянутих вище схем. Після відповідних перетворювань одержимо рівняння для механічної характеристики в замкненій СК: ( 1. 16) де к = кс / с – коефіцієнт передачі (підсилення) всієї системи; Rя = Rтп + Rд. При постійному коефіцієнті передачі k механічні характеристики двигуна лінійні. Перший член рівняння (1. 16) визначає кутову швидкість ідеального х. х. двигуна, а другий – падіння кутової швидкості, зумовлене зміною моменту навантаження. Статизм системи знаходиться (при М = Мном) за формулою ( 1. 17)
де Uзс – задавальна напруга в системі з ЗЗ по ω; γ = Uзз / ω – коефіцієнт передачі ЗЗ по ω. Усі інші позначення ті самі, що і для розглянутих вище схем. Після відповідних перетворювань одержимо рівняння для механічної характеристики в замкненій СК: ( 1. 16) де к = кс / с – коефіцієнт передачі (підсилення) всієї системи; Rя = Rтп + Rд. При постійному коефіцієнті передачі k механічні характеристики двигуна лінійні. Перший член рівняння (1. 16) визначає кутову швидкість ідеального х. х. двигуна, а другий – падіння кутової швидкості, зумовлене зміною моменту навантаження. Статизм системи знаходиться (при М = Мном) за формулою ( 1. 17)
 Із (1. 17) виходить, що статизм може бути як завгодно малим зі збільшенням коефіцієнта передачі всієї системи. Тому в системі з ВЗЗ по ω можливо при високому коефіцієнті передачі отримати значний діапазон регулювання. На рис. 1. 6, б показані: гранична х-ка 1 при к → ∞; х-ки 2, 2΄ при кінцевих значеннях k і х-ка двигуна 3 в розімкненій системі. Використання комбінованих ЗЗ – розширює можливості ЕП щодо діапазону регулювання, наприклад, можливе з΄єднання ЖВЗЗ по напрузі з додатним ЗЗ по струму або ВЗЗ по кутовій швидкості з додатним ЗЗ по струму. Такі ж ЗЗ можуть бути в СКЕП змінного струму. У якості перетворювача в системах, що розглядаються, можуть бути використані різні пристрої: Г-Д, керований випрямляч, магнітний підсилювач, Ш І П та ін. Збільшення коефіцієнта підсилення в розглядуваних системах обмежено їх динамічною стійкістю та чутливістю до перешкод. При високих коефіцієнтах підсилення доводиться вводити допоміжні корегуючі пристрої або стабілізуючі ЗЗ, які роблять систему стійкою та забезпечують потрібну якість (час процесу перерегулювання, коливальні процеси) перехідних процесів у системі (зміна задавання по швидкості, накидання-зняття навантаження та ін. ). Обмеженням на коефіцієнт підсилення системи є також і обмеження діапазону регулювання. Так, для системи з ЗЗ по швидкості, яка має найкращу стабільність при всіх можливих збурюваннях (зміна потоку двигуна, навантаження, температури обмоток, напруги мережі й ін. ), серед розглянутих систем найбільший діапазон регулювання становить близько 2000 : 1.
Із (1. 17) виходить, що статизм може бути як завгодно малим зі збільшенням коефіцієнта передачі всієї системи. Тому в системі з ВЗЗ по ω можливо при високому коефіцієнті передачі отримати значний діапазон регулювання. На рис. 1. 6, б показані: гранична х-ка 1 при к → ∞; х-ки 2, 2΄ при кінцевих значеннях k і х-ка двигуна 3 в розімкненій системі. Використання комбінованих ЗЗ – розширює можливості ЕП щодо діапазону регулювання, наприклад, можливе з΄єднання ЖВЗЗ по напрузі з додатним ЗЗ по струму або ВЗЗ по кутовій швидкості з додатним ЗЗ по струму. Такі ж ЗЗ можуть бути в СКЕП змінного струму. У якості перетворювача в системах, що розглядаються, можуть бути використані різні пристрої: Г-Д, керований випрямляч, магнітний підсилювач, Ш І П та ін. Збільшення коефіцієнта підсилення в розглядуваних системах обмежено їх динамічною стійкістю та чутливістю до перешкод. При високих коефіцієнтах підсилення доводиться вводити допоміжні корегуючі пристрої або стабілізуючі ЗЗ, які роблять систему стійкою та забезпечують потрібну якість (час процесу перерегулювання, коливальні процеси) перехідних процесів у системі (зміна задавання по швидкості, накидання-зняття навантаження та ін. ). Обмеженням на коефіцієнт підсилення системи є також і обмеження діапазону регулювання. Так, для системи з ЗЗ по швидкості, яка має найкращу стабільність при всіх можливих збурюваннях (зміна потоку двигуна, навантаження, температури обмоток, напруги мережі й ін. ), серед розглянутих систем найбільший діапазон регулювання становить близько 2000 : 1.


