Лекция 2. Проецирование плоскости 1.

Лекция 2. Проецирование плоскости 1. Способы задания плоскости. 2. Общее и частное положение плоскости в пространстве. 3. Принадлежность точки и линии плоскости. 4. Главные линии плоскости. 5. Взаимное положение плоскостей. 1

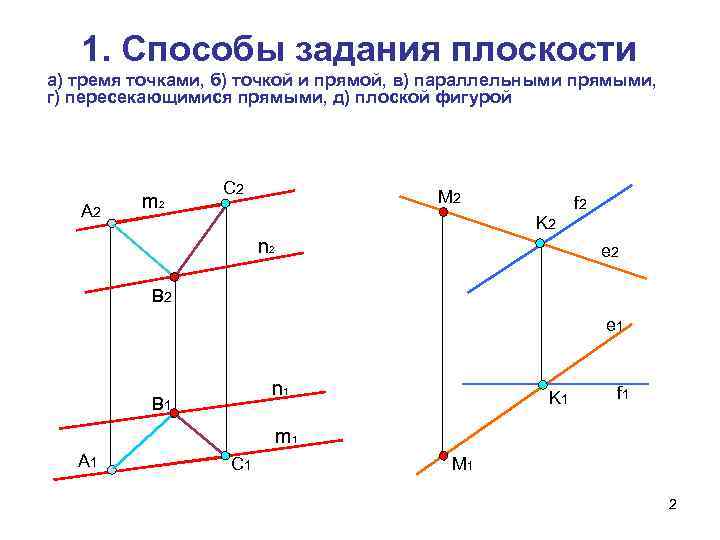
1. Способы задания плоскости а) тремя точками, б) точкой и прямой, в) параллельными прямыми, г) пересекающимися прямыми, д) плоской фигурой С 2 m 2 М 2 f 2 А 2 K 2 n 2 e 2 В 2 e 1 n 1 K 1 f 1 В 1 m 1 А 1 С 1 М 1 2

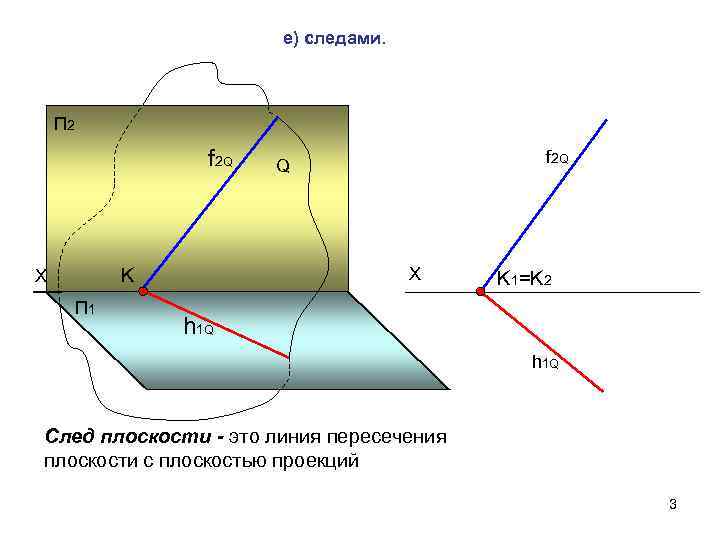
е) следами. П 2 f 2 Q Q f 2 Q Х K Х K 1=K 2 П 1 h 1 Q След плоскости - это линия пересечения плоскости с плоскостью проекций 3

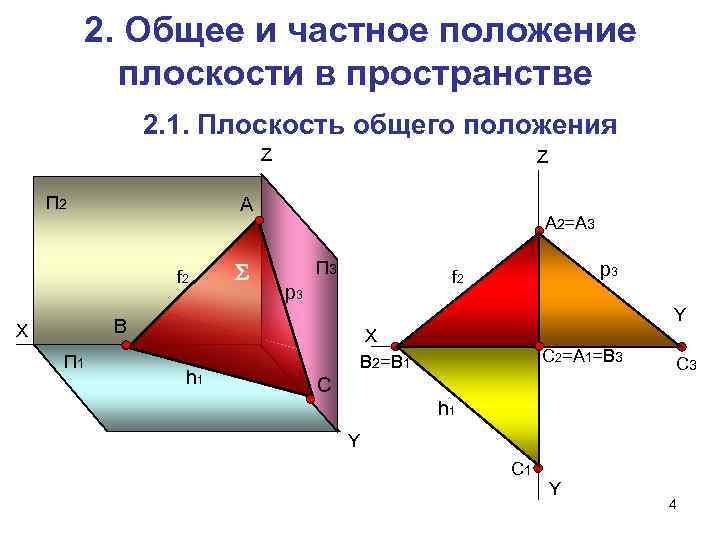
2. Общее и частное положение плоскости в пространстве 2. 1. Плоскость общего положения Z П 2 А 2=А 3 f 2 П 3 f 2 p 3 Y Х В X П 1 В 2=В 1 С 2=А 1=В 3 С 3 h 1 С h 1 Y С 1 Y 4

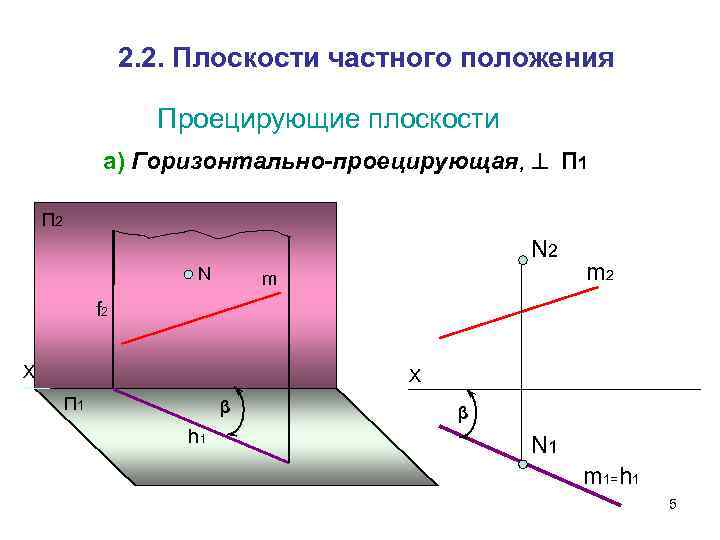
2. 2. Плоскости частного положения Проецирующие плоскости а) Горизонтально-проецирующая, П 1 П 2 N m 2 f 2 Х Х П 1 β h 1 N 1 m 1=h 1 5

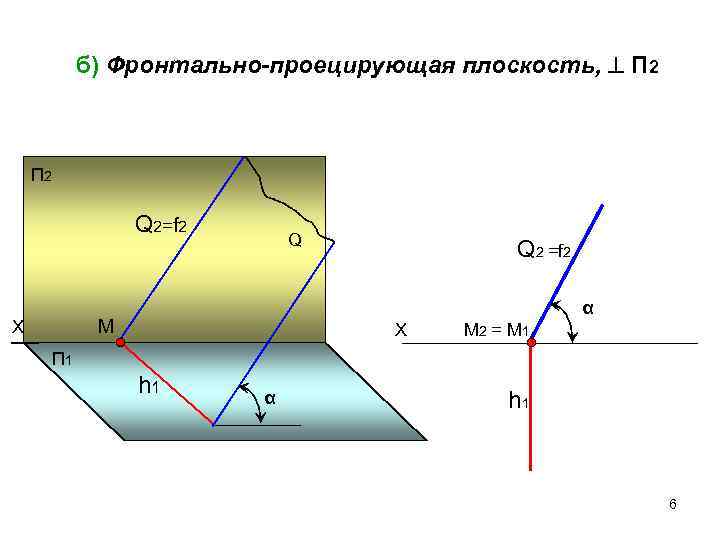
б) Фронтально-проецирующая плоскость, П 2 Q 2= f 2 Q 2 =f 2 α Х M Х M 2 = M 1 П 1 h 1 α h 1 6

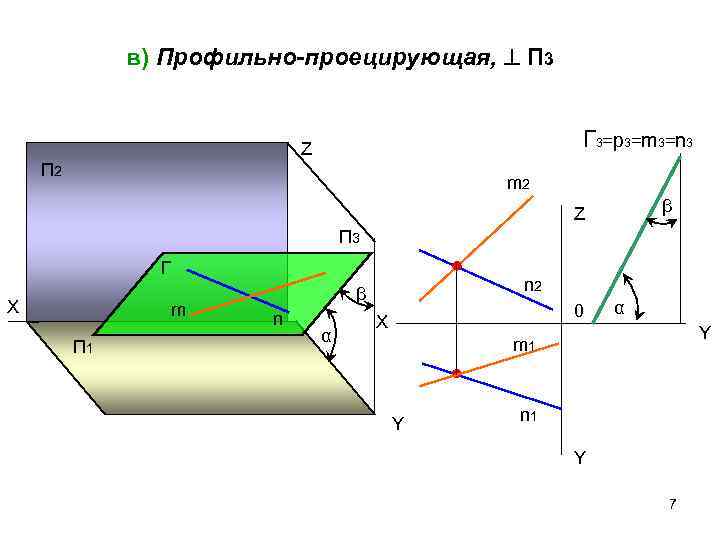
в) Профильно-проецирующая, П 3 Z Г 3=р3=m 3=n 3 П 2 m 2 Z β П 3 Г β n 2 Х m 0 α n Х α Y П 1 m 1 Y n 1 Y 7

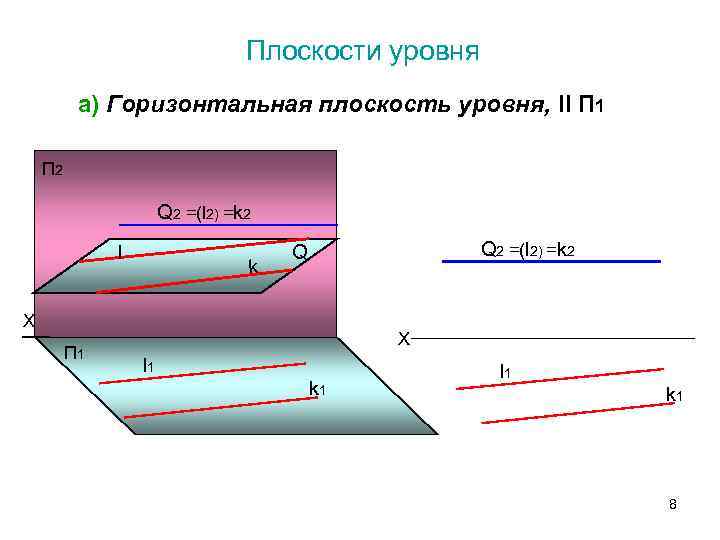
Плоскости уровня а) Горизонтальная плоскость уровня, ll П 1 П 2 Q 2 =(l 2) =k 2 l Q 2 =(l 2) =k 2 k Х П 1 l 1 k 1 8

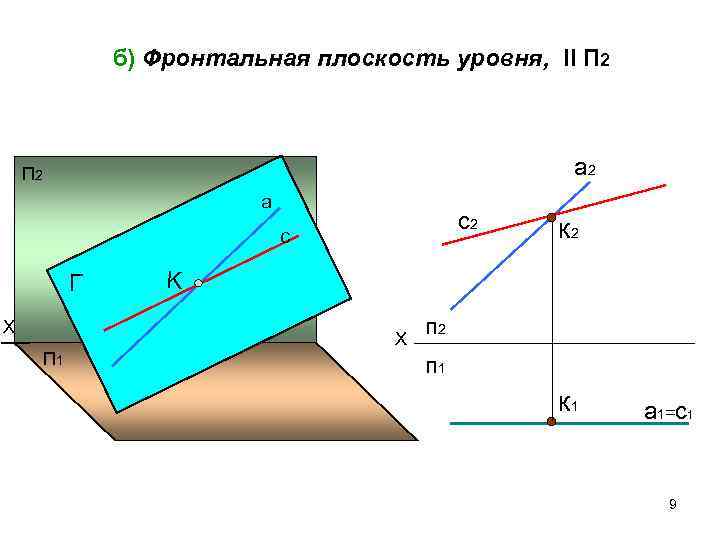
б) Фронтальная плоскость уровня, ll П 2 а 2 а с2 к 2 с Г K Х п 2 П 1 п 1 к 1 a 1=с1 9

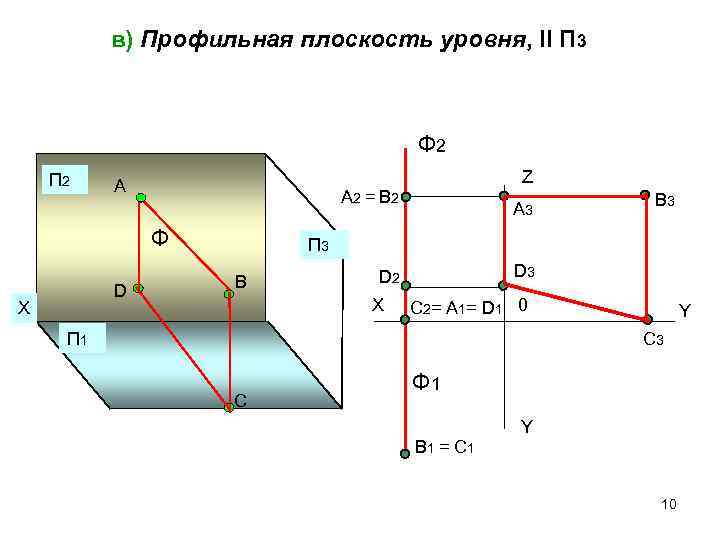
в) Профильная плоскость уровня, ll П 3 Ф 2 П 2 А Z А 2 = В 2 В 3 А 3 Ф П 3 D 2 D 3 D В Х Х С 2= А 1= D 1 0 Y П 1 С 3 Ф 1 С Y В 1 = С 1 10

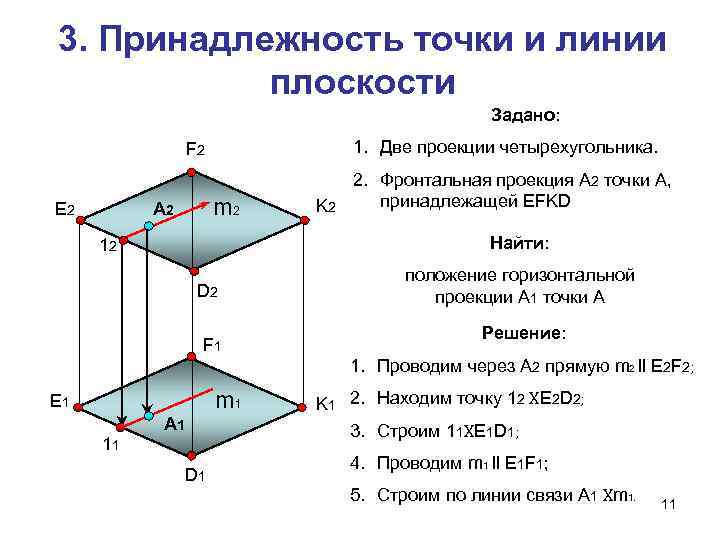
3. Принадлежность точки и линии плоскости Задано: F 2 1. Две проекции четырехугольника. 2. Фронтальная проекция А 2 точки А, Е 2 А 2 m 2 K 2 принадлежащей EFKD 12 Найти: положение горизонтальной D 2 проекции А 1 точки А Решение: F 1 1. Проводим через A 2 прямую m 2 ll E 2 F 2; Е 1 m 1 K 1 2. Находим точку 12 XE 2 D 2; А 1 3. Строим 11 XE 1 D 1; 11 4. Проводим m 1 ll E 1 F 1; D 1 5. Строим по линии связи А 1 Xm 1. 11

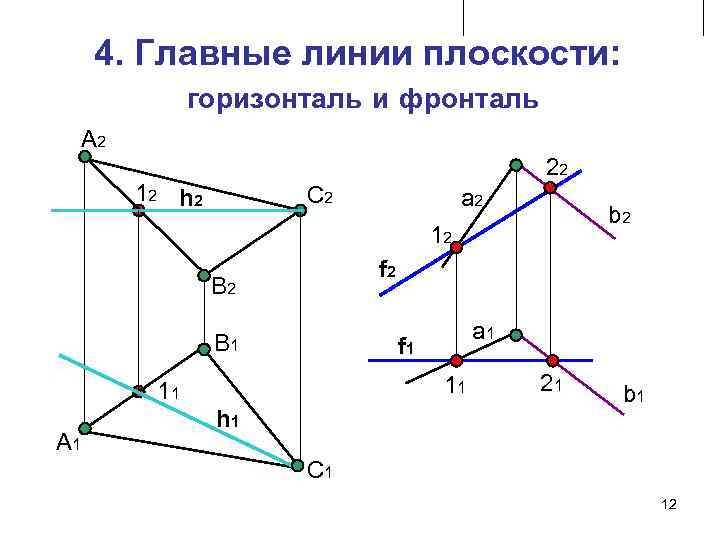
4. Главные линии плоскости: горизонталь и фронталь A 2 22 12 h 2 C 2 a 2 b 2 12 f 2 B 2 B 1 a 1 f 1 11 11 21 b 1 h 1 A 1 C 1 12

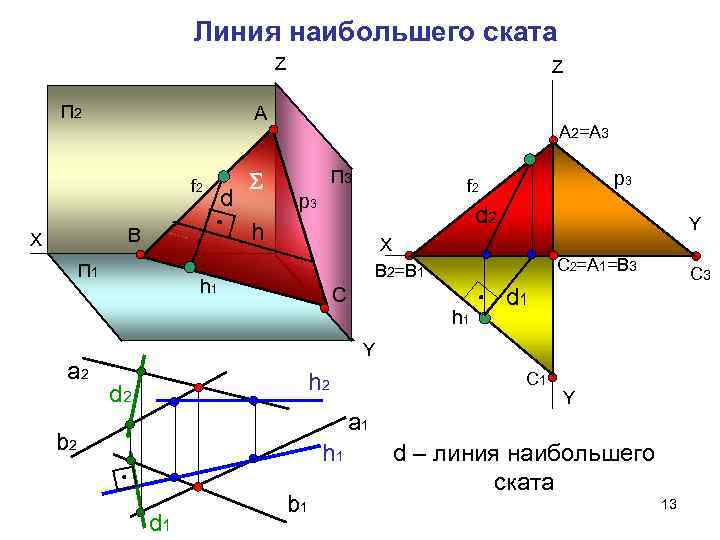
Линия наибольшего ската Z П 2 А 2=А 3 f 2 П 3 f 2 p 3 d p 3 d 2 Y Х В h X П 1 В 2=В 1 С 2=А 1=В 3 С 3 h 1 С d 1 h 1 Y a 2 h 2 С 1 d 2 Y a 1 b 2 h 1 d – линия наибольшего ската b 1 13 d 1

5. Взаимное положение плоскостей Плоскости в пространстве могут быть параллельны или пересекаться. 1. Параллельность плоскостей. Для параллельности плоскостей достаточно, чтобы две пересекающиеся прямые одной плоскости были параллельны двум пересекающимся прямым другой плоскости. 2. Пересечение плоскостей. Результатом пересечения двух плоскостей является прямая линия, для построения которой достаточно найти две точки, общие для пересекающихся плоскостей. 3. Перпендикулярность плоскостей. Две плоскости взаимно перпендикулярны, если одна из них содержит перпендикуляр к другой. Прямая, перпендикулярная плоскости, называется нормалью плоскости и перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости. 14

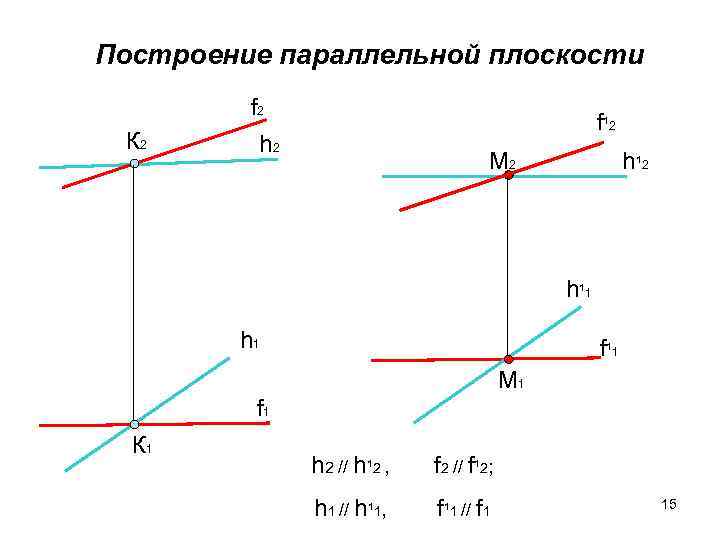
Построение параллельной плоскости f 2 f ¹ 2 К 2 h 2 M 2 h ¹ 2 h ¹ 1 h 1 f ¹ 1 M 1 f 1 К 1 h 2 // h¹ 2 , f 2 // f¹ 2; h 1 // h¹ 1, f¹ 1 // f 1 15

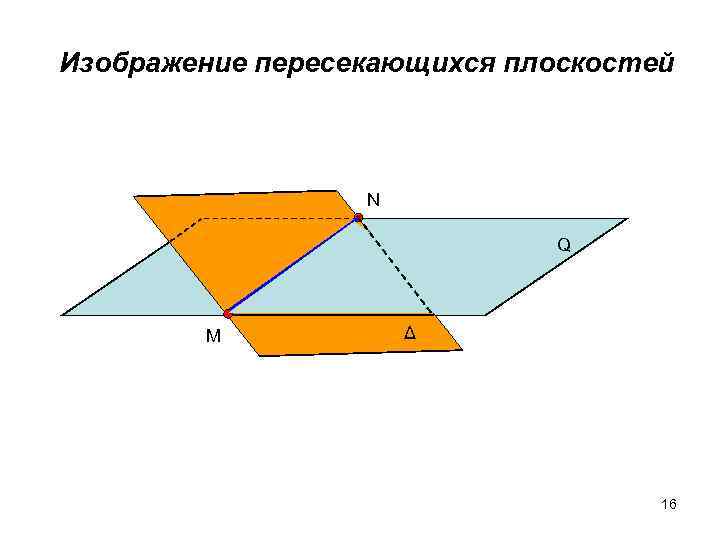
Изображение пересекающихся плоскостей N Q M Δ 16

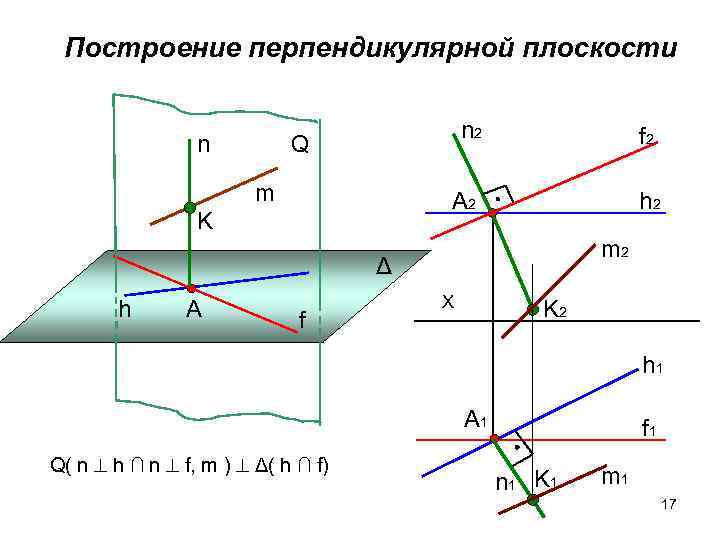
Построение перпендикулярной плоскости n 2 f 2 n Q m A 2 h 2 K m 2 Δ h А Х K 2 f h 1 A 1 f 1 Q( n h ∩ n f, m ) Δ( h ∩ f) n 1 K 1 m 1 17

Желаю здравствовать! Читайте литературу! Не пренебрегайте самостоятельной работой! 18