Лекция 2 ПРИБЛИЖЕННЫЕ АНАЛИТИЧЕСКИЕ ФУНКЦИИ АТОМНЫХ ОРБИТАЛЕЙ

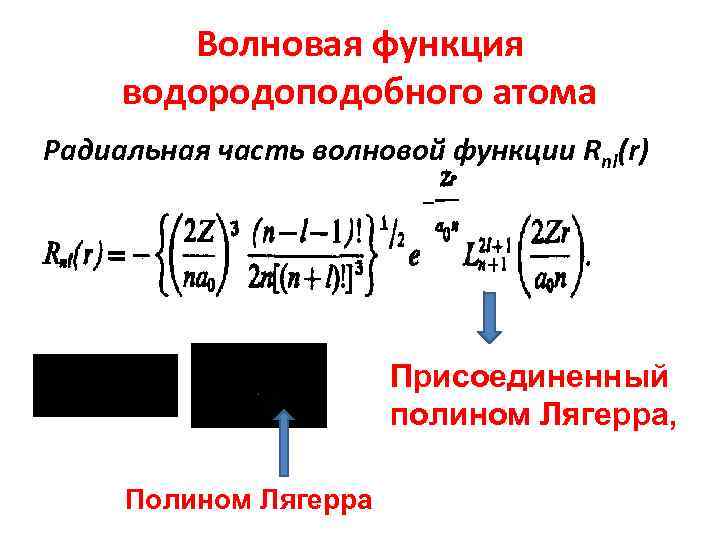
Волновая функция водородоподобного атома Радиальная часть волновой функции Rnl(r) Присоединенный полином Лягерра, Полином Лягерра

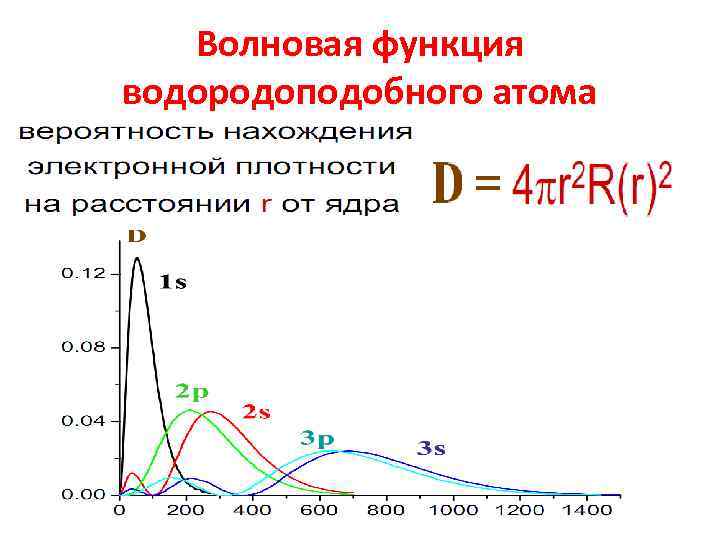
Волновая функция водородоподобного атома

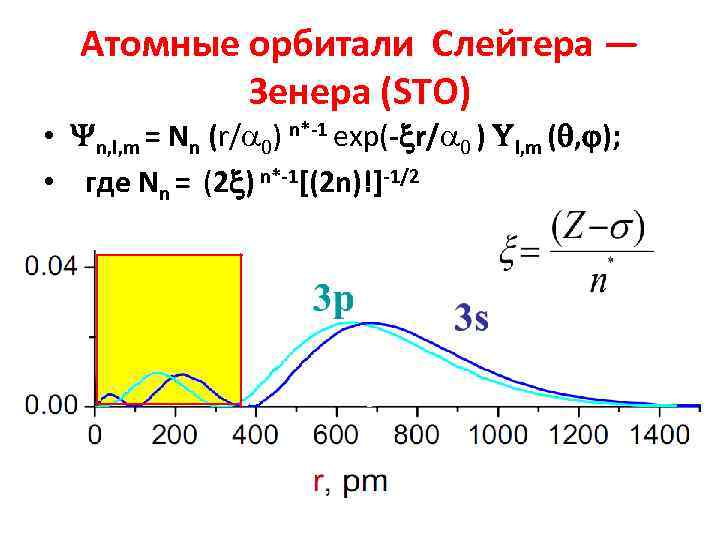
Атомные орбитали Слейтера — Зенера (STO) • n, l, m = Nn (r/ 0) n*-1 exp(- r/ 0 ) l, m ( , ); • где Nn = (2 ) n*-1[(2 n)!]-1/2

экр и n* • Константы экранирования экр для элементов второго периода до атома фтора были вычислены Зенером. • Слейтер аппроксимировал экр и n* для всех элементов таблицы Д. И. Менделеева по экспериментальными данным рентгеновской спектроскопии атома.

Двухэкспоненциальные АО • Радиальные функции слейтеровского типа недостаточно описывают поведение на небольших расстояниях от ядра n, l, m = N(r n*-1 e- 1 r + r n*-1 e- 2 r ) l, m ( , ) Эти функции называют дубль-зетафункциями, а базисный набор, построенный на них, называется дубль-зета-базисом (DZ).

Гауссовские функции • При расчетах волновых функций молекул широкое распространение получили гауссовские функции типа • Gn, l, m = Nn( )r n -1 exp(- r 2 ) l, m ( , ) Nn — нормировочный множитель; — варьируемый параметр. • для s-орбиталей: G= N 1( )*ехр(- г 2); • для px-орбиталей: G= N 1( )* r*exp(- r 2)

Гауссовские функции (G-AO) • Такие функции называются примитивными гауссовые функции. • Гауссовых орбиталей приходится брать намного больше, чем слейтеровских (сгруппированные базисы). STO = Gi

Сгруппированные наборы G-AO • Для изучения реакционной способности и строения органических соединений наиболее широко используются базисы, предложенные Поплом с сотрудниками: • Минимальный базис – STO -3 G • Аналогично STO -4 G или STO -5 G

Валентно- расщепленные базисы • STO 3 -21 G • STO 4 -21 G STO N-ML G Пример STO 6 -31 G • каждая STO для (e) внутренних оболочек аппроксимирована линейной комбинацией из 6 G-AO, • а для валентных (e) вместо каждой STO используются две линейные комбинации G-AO : одна — из 3 G-AO , а другая — из одной 1 G-AO

Валентно-расщепленные базисы с поляризационными функциями • STO 6 -31 G* для всех атомов кроме Н • Для р элементов I, III периодов STO 6 -31 G* STO 6 -31 G(p, d) • STO 6 -31 G ** включая атом Н • Для атома Н -> 2 p 0 STO 6 -31 G ** STO 6 -31 G(s, p)

Валентно-расщепленные базисы с диффузионными функциями Для расчета систем с участием ионов • STO 6 -31+G для всех атомов кроме Н • STO 6 -31++G включая атом Н • Диффузионные функции – это такие же валентных АО, только с меньшими значения • STO 6 -31++G**

Выводы • Все неэмпирические квантово-химические методы являются в большей или меньшей степени приближенными. • Результаты расчета очень сильно зависят от выбора базиса (БАО). • Увеличение БАО обычно позволяет точнее передать распределение электронной плотности в молекулах и его изменение в ходе химических реакций.

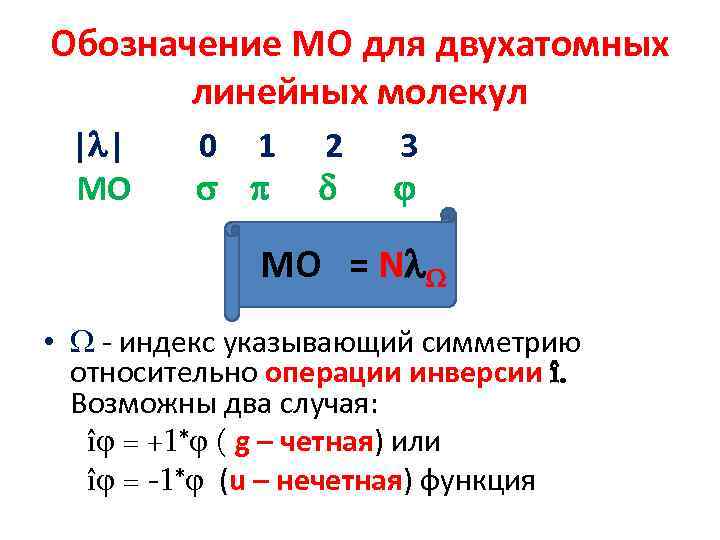
Обозначение МО для двухатомных линейных молекул | | МО 0 1 2 3 МО = N • - индекс указывающий симметрию относительно операции инверсии î. Возможны два случая: î = +1* ( g – четная) или î = -1* (u – нечетная) функция

Теория направленных валентностей. • • • Тип ГО Геометрия sp линейная sp 2 плоский треугольник sp 2 d dsp 2 плоский квадрат sp 3 тетраэдр sp 3 d тригональная бипирамида sp 3 d 2 октаэдр

Теория отталкивания электронных пар валентных оболочек(ОЭПВО) в ММО Конфигурация молекулы и ее геометрическое строение определяется конфигурацией связей, каждая из которых рассматривается как двухцентровая локализованная МО.

• Конфигурация связей центрального атома А в зависимости от числа электронных пар q на его валентных орбиталях q 2 Конфигурация Линейная q Конфигурация 8 9 3 Квадратная антипризма Тригональная антипризма с тремя дополнительными вершинами Треугольник 4 Тетраэдр 10 5 Тригональная бипирамида 11 Квадратная антипризма с двумя дополнительными вершинами Икосаэдр без одной вершины 6 Октаэдр 12 Икосаэдр 7 Октаэдр вершиной с дополнительной

Применение теории симметрии в квантово-химических расчетах • • • Элементы симметрии Ri Единица или единичный элемент Е. Ось вращения n-го порядка Сn. Плоскость отражения . Зеркально- поворотная ось n-го порядка Sn Инверсия – i.

Операции симметрии • Элементы симметрии порождают наборы операций симметрии ☭ - Ŕ. • Количество операций симметрии равно или больше числа элементов симметрии. Например, элемент С 3 порождает две операции симметрии С 3 , С 32

Группа симметрии молекулы • Совокупность операций симметрии R 1, R 2, R 3, … Rn , которая удовлетворяет ряду требованиям. • Произведение любых операций симметрии группы является также ее операцией. R 1* R 2 = R 3

Введем еще два понятия : • эквивалентные атомы – одноименные атомы переходящие при операциях симметрии друг в друга. • эквивалентные операции симметрии которые можно получить неким преобразованием координат (перестановкой координат или атомом). Эквивалентные операции симметрии всегда порождены одним и тем же элементом симметрии.

Точечные группы Щёнфлиса • Номенклатура Шёнфлиса. Главной частью каждого обозначения группы является заглавная буква: • С (циклическая), • D (диэдрическая), • О (октаэдрическая) • Т (тетраэдрическая).

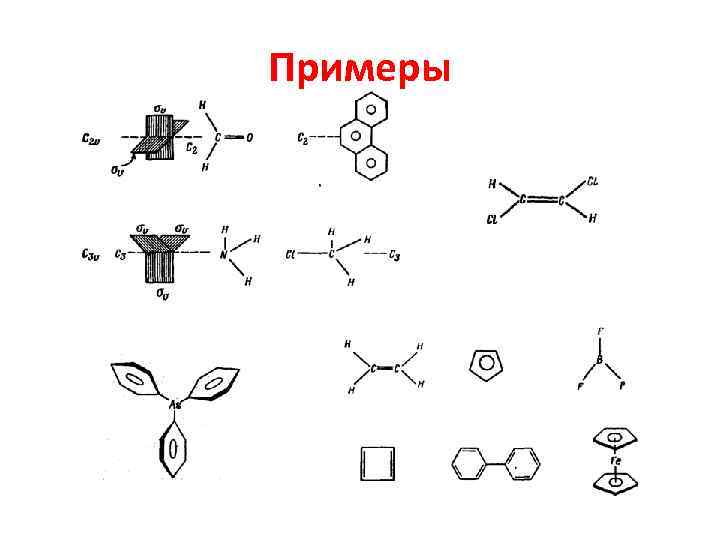
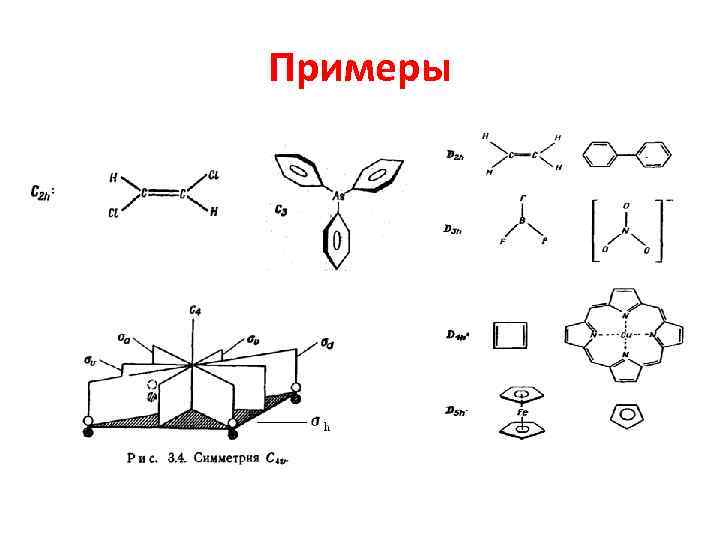
Примеры

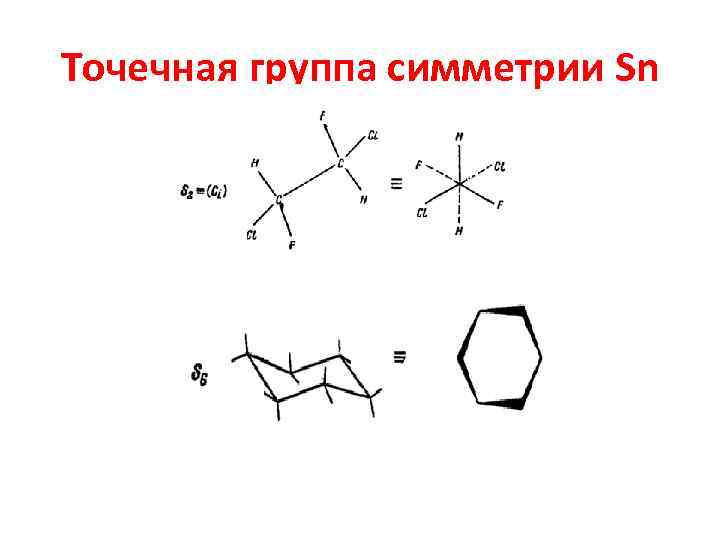
Точечная группа симметрии Sn

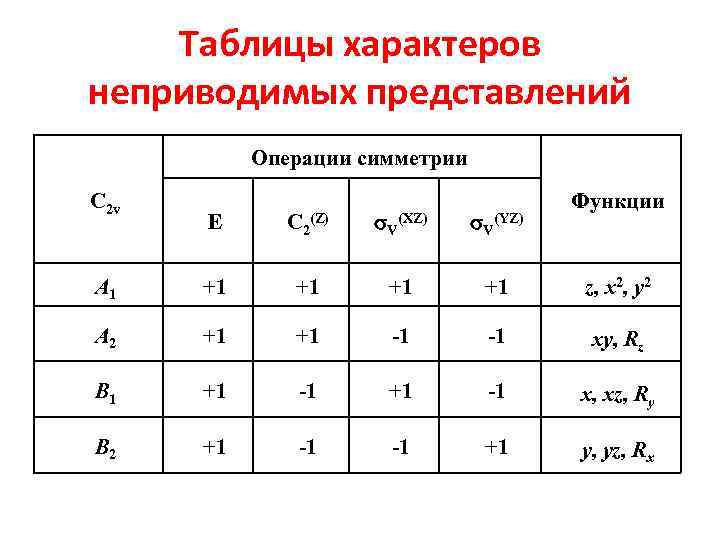
Таблицы характеров неприводимых представлений Операции симметрии С 2 v Е C 2 (Z) V (XZ) V (YZ) Функции А 1 +1 +1 z, x 2, y 2 А 2 +1 +1 -1 -1 xy, Rz В 1 +1 -1 x, xz, Ry В 2 +1 -1 -1 +1 y, yz, Rx

Операции симметрии С 3 v Функции Е 2 C 3(Z) 3 v А 1 +1 +1 +1 z, x 2+y 2 A 2 +1 +1 -1 Rz 0 x, y, x 2 -y 2, xz, yz, xy, Rx, Ry E 2 -1

Cимметрия молекулярных орбиталей • Под симметрией молекулярных орбиталей принимают тип неприводимого представления (НП) данной точечной группы.

Пример •