Лекція 2 ПОТОКИ

















































 Лекція 2 ПОТОКИ ВИКЛИКІВ Основні питання 1 Поняття потоків викликів і основні способи їхнього задання 2. Класифікація потоків викликів відповідно до їх властивостей 3. Основні класи потоків. Найпростіші потоки
Лекція 2 ПОТОКИ ВИКЛИКІВ Основні питання 1 Поняття потоків викликів і основні способи їхнього задання 2. Класифікація потоків викликів відповідно до їх властивостей 3. Основні класи потоків. Найпростіші потоки
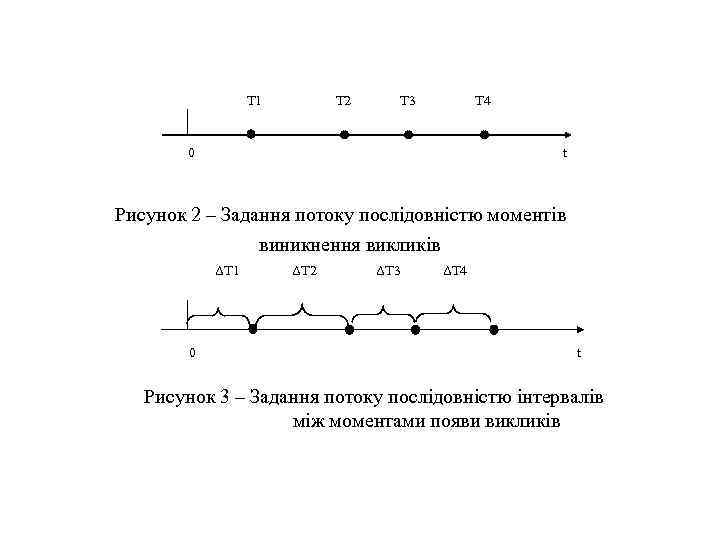
 Поняття потоків викликів і основні способи їхнього задання • Потоком викликів (заявок) називається послідовність викликів (заявок), що надходять на СРІ в деякі моменти часу [1 -5]. • Потоки можуть бути детермінованими або випадковими. • Детермінований потік – це потік викликів з фіксованими моментами їхнього надходження. Такий потік рідко зустрічається. • Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. Випадковий потік може бути заданий трьома еквівалентними способами: • 1) послідовністю моментів виникнення викликів (див. рис. 2); • 2) послідовністю інтервалів між сусідніми викликами (див. рис. 3); • 3) цілочисленним процесом, що визначає кількість викликів, які надійшли протягом часу [t 0, t) (див. рис. 4).
Поняття потоків викликів і основні способи їхнього задання • Потоком викликів (заявок) називається послідовність викликів (заявок), що надходять на СРІ в деякі моменти часу [1 -5]. • Потоки можуть бути детермінованими або випадковими. • Детермінований потік – це потік викликів з фіксованими моментами їхнього надходження. Такий потік рідко зустрічається. • Якщо моменти надходження викликів залежать від випадкових факторів, то потік називається випадковим. Випадковий потік може бути заданий трьома еквівалентними способами: • 1) послідовністю моментів виникнення викликів (див. рис. 2); • 2) послідовністю інтервалів між сусідніми викликами (див. рис. 3); • 3) цілочисленним процесом, що визначає кількість викликів, які надійшли протягом часу [t 0, t) (див. рис. 4).
 T 1 T 2 T 3 T 4 0 t Рисунок 2 – Задання потоку послідовністю моментів виникнення викликів ΔT 1 ΔT 2 ΔT 3 ΔT 4 0 t Рисунок 3 – Задання потоку послідовністю інтервалів між моментами появи викликів
T 1 T 2 T 3 T 4 0 t Рисунок 2 – Задання потоку послідовністю моментів виникнення викликів ΔT 1 ΔT 2 ΔT 3 ΔT 4 0 t Рисунок 3 – Задання потоку послідовністю інтервалів між моментами появи викликів
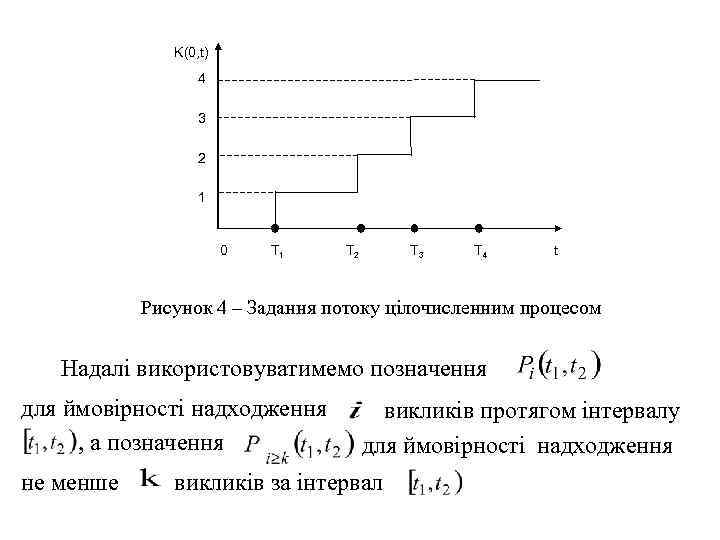
 K(0, t) 4 3 2 1 0 T 1 T 2 T 3 T 4 t Рисунок 4 – Задання потоку цілочисленним процесом Надалі використовуватимемо позначення для ймовірності надходження викликів протягом інтервалу , а позначення для ймовірності надходження не менше викликів за інтервал
K(0, t) 4 3 2 1 0 T 1 T 2 T 3 T 4 t Рисунок 4 – Задання потоку цілочисленним процесом Надалі використовуватимемо позначення для ймовірності надходження викликів протягом інтервалу , а позначення для ймовірності надходження не менше викликів за інтервал
 Числові характеристики потоків: провідна функція, інтенсивність і параметр потоку • Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. • До основних числових характеристик потоків викликів належать: провідна функція потоку, інтенсивність і параметр потоку. • Провідною функцією потоку Λ(t) називається математичне очікування числа викликів, що надійшли за інтервал часу , тобто . • Згідно з означенням, (1)
Числові характеристики потоків: провідна функція, інтенсивність і параметр потоку • Імовірнісний опис потоку викликів може бути виконаний з використанням багатовимірних функцій розподілу обраних характеристик потоку. • До основних числових характеристик потоків викликів належать: провідна функція потоку, інтенсивність і параметр потоку. • Провідною функцією потоку Λ(t) називається математичне очікування числа викликів, що надійшли за інтервал часу , тобто . • Згідно з означенням, (1)
 Провідна функція невід’ємна й неспадна. Потоки з неперервною провідною функцією називаються регулярними, а зі східчастою – сингулярними. • Під параметром потоку у момент часу розуміється величина (2) . Під інтенсивністю потоку розуміється середнє число викликів за одиницю часу: . (3) Для будь-яких потоків , причому для так званих ординарних потоків .
Провідна функція невід’ємна й неспадна. Потоки з неперервною провідною функцією називаються регулярними, а зі східчастою – сингулярними. • Під параметром потоку у момент часу розуміється величина (2) . Під інтенсивністю потоку розуміється середнє число викликів за одиницю часу: . (3) Для будь-яких потоків , причому для так званих ординарних потоків .
 Класифікація потоків викликів відповідно до їх властивостей • Потоки викликів класифікуються згідно з такими властивостями, як однорідність, стаціонарність, ординарність і післядія. Розглянемо ці властивості. • 1. У неоднорідному потоці кожен виклик має дві і більше характеристики. Наприклад, виклики, що надходять від абонентів телефонної мережі, характеризуються моментами їхнього надходження, напрямками встановлення з'єднань, тривалістю обслуговування й іншими характеристиками. • Однорідний потік характеризується лише моментами надходження викликів. • На практиці потоки викликів, як правило, є неоднорідними. Однак у теорії розглядаються однорідні потоки, якщо відсутні спеціальні застереження. • 2. Властивість стаціонарності потоку означає, що його ймовірнісні характеристики не змінюються в часі.
Класифікація потоків викликів відповідно до їх властивостей • Потоки викликів класифікуються згідно з такими властивостями, як однорідність, стаціонарність, ординарність і післядія. Розглянемо ці властивості. • 1. У неоднорідному потоці кожен виклик має дві і більше характеристики. Наприклад, виклики, що надходять від абонентів телефонної мережі, характеризуються моментами їхнього надходження, напрямками встановлення з'єднань, тривалістю обслуговування й іншими характеристиками. • Однорідний потік характеризується лише моментами надходження викликів. • На практиці потоки викликів, як правило, є неоднорідними. Однак у теорії розглядаються однорідні потоки, якщо відсутні спеціальні застереження. • 2. Властивість стаціонарності потоку означає, що його ймовірнісні характеристики не змінюються в часі.
 • Потік викликів називається стаціонарним, якщо при будь- якому спільна ймовірність надходження викликів за інтервали часу …, не залежить від початкового моменту часу . Для стаціонарного потоку його параметр та інтенсивність постійні: . Потік, що не має властивості стаціонарності, називається нестаціонарним. 3. Потік викликів називається ординарним , якщо в ньому неможливе одночасне надходження двох і більше викликів, тобто виконується така умова: (4)
• Потік викликів називається стаціонарним, якщо при будь- якому спільна ймовірність надходження викликів за інтервали часу …, не залежить від початкового моменту часу . Для стаціонарного потоку його параметр та інтенсивність постійні: . Потік, що не має властивості стаціонарності, називається нестаціонарним. 3. Потік викликів називається ординарним , якщо в ньому неможливе одночасне надходження двох і більше викликів, тобто виконується така умова: (4)
 • Потік, що не має цієї властивості, називається неординарним. • Приклад ординарного потоку – потік викликів, що надходить на АТС від великої групи абонентів, а прикладами неординарних потоків є потоки телеграм у кілька адрес. • 4. Потік викликів називається потоком без післядії, якщо для будь-якого сумісна ймовірність надходження , викликів за відповідні інтервали , (5) не залежить від процесу надходження викликів до початкового моменту часу t.
• Потік, що не має цієї властивості, називається неординарним. • Приклад ординарного потоку – потік викликів, що надходить на АТС від великої групи абонентів, а прикладами неординарних потоків є потоки телеграм у кілька адрес. • 4. Потік викликів називається потоком без післядії, якщо для будь-якого сумісна ймовірність надходження , викликів за відповідні інтервали , (5) не залежить від процесу надходження викликів до початкового моменту часу t.
 • Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. • Прикладом потоку без післядії може служити потік телефонних викликів, що надходять від великої групи джерел. Це пов'язано з тим, що лише невелика частина (10 -20%) абонентської групи водночас бере участь у з'єднаннях. • Потоки, які не мають властивості відсутності післядії, називаються потоками з післядією. • Потоки викликів від спарених телефонних апаратів і потоки викликів від малих абонентських груп є прикладами потоків з післядією.
• Іншими словами, відсутність післядії потоку означає незалежність плину випадкового потоку викликів після деякого моменту часу від його плину до цього моменту. • Прикладом потоку без післядії може служити потік телефонних викликів, що надходять від великої групи джерел. Це пов'язано з тим, що лише невелика частина (10 -20%) абонентської групи водночас бере участь у з'єднаннях. • Потоки, які не мають властивості відсутності післядії, називаються потоками з післядією. • Потоки викликів від спарених телефонних апаратів і потоки викликів від малих абонентських груп є прикладами потоків з післядією.
 Основні класи потоків Найпростіші потоки • Найпростішим потоком називається стаціонарний ординарний потік без післядії. Цей потік є основною моделлю в теорії телетрафіку. • Для найпростішого потоку справедлива теорема. • Теорема 1. Надходження викликів за інтервал часу тривалістю у найпростішому потоці підпорядковується розподілу Пуассона з імовірностями , (6) де – імовірність того, що за інтервал часу довжиною надійде викликів; – параметр найпростішого потоку.
Основні класи потоків Найпростіші потоки • Найпростішим потоком називається стаціонарний ординарний потік без післядії. Цей потік є основною моделлю в теорії телетрафіку. • Для найпростішого потоку справедлива теорема. • Теорема 1. Надходження викликів за інтервал часу тривалістю у найпростішому потоці підпорядковується розподілу Пуассона з імовірностями , (6) де – імовірність того, що за інтервал часу довжиною надійде викликів; – параметр найпростішого потоку.
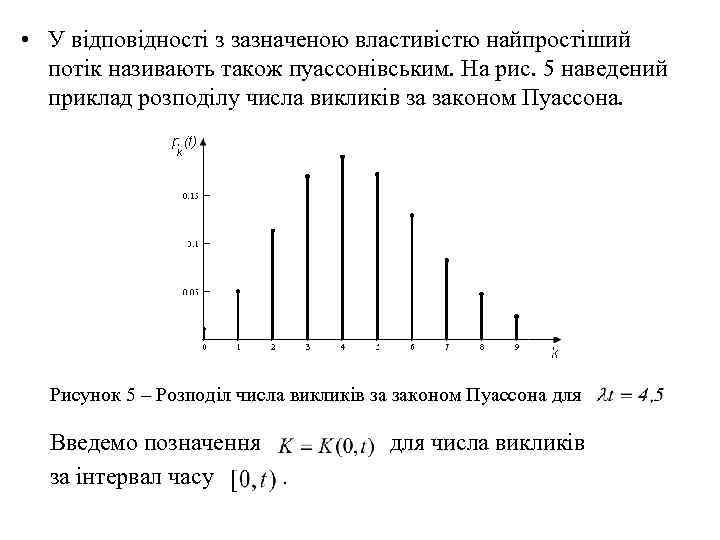
 • У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона. Рисунок 5 – Розподіл числа викликів за законом Пуассона для Введемо позначення для числа викликів за інтервал часу .
• У відповідності з зазначеною властивістю найпростіший потік називають також пуассонівським. На рис. 5 наведений приклад розподілу числа викликів за законом Пуассона. Рисунок 5 – Розподіл числа викликів за законом Пуассона для Введемо позначення для числа викликів за інтервал часу .
 • Тоді із властивостей розподілу Пуассона випливають такі наслідки. • 1. . • 2. Імовірності пов'язані між собою рекурентним співвідношенням , (7) де . 3. Послідовність імовірностей , з розподілу Пуассона при монотонно спадає зі зростанням . Якщо , то зі зростанням імовірності спочатку монотонно зростають до досягнення моди або двох модальних значень, а потім монотонно спадають.
• Тоді із властивостей розподілу Пуассона випливають такі наслідки. • 1. . • 2. Імовірності пов'язані між собою рекурентним співвідношенням , (7) де . 3. Послідовність імовірностей , з розподілу Пуассона при монотонно спадає зі зростанням . Якщо , то зі зростанням імовірності спочатку монотонно зростають до досягнення моди або двох модальних значень, а потім монотонно спадають.
 • Якщо дрібне число, то мода , де – ціла частина числа , якщо ж ціле, то розподіл має дві моди: ; . 4. Зі зростанням добутку обвідна значень , наближається до нормального розподілу. Вже при =10 має місце добра апроксимація такої обвідної нормальним розподілом: (8)
• Якщо дрібне число, то мода , де – ціла частина числа , якщо ж ціле, то розподіл має дві моди: ; . 4. Зі зростанням добутку обвідна значень , наближається до нормального розподілу. Вже при =10 має місце добра апроксимація такої обвідної нормальним розподілом: (8)
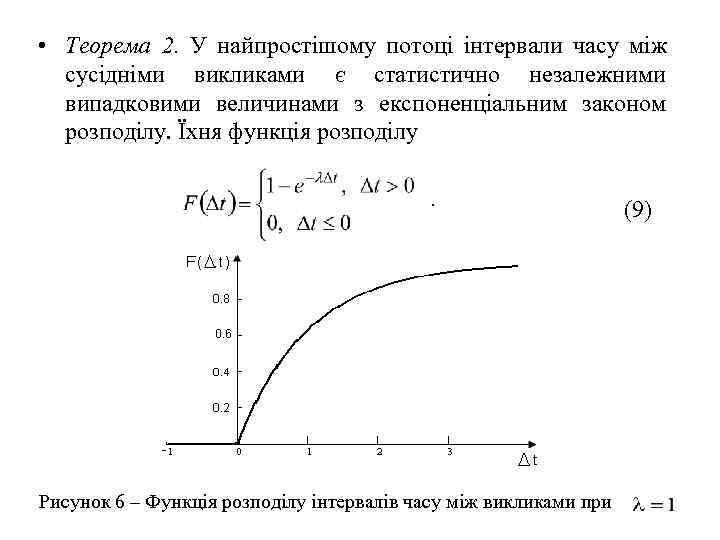
 • Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу (9) Рисунок 6 – Функція розподілу інтервалів часу між викликами при
• Теорема 2. У найпростішому потоці інтервали часу між сусідніми викликами є статистично незалежними випадковими величинами з експоненціальним законом розподілу. Їхня функція розподілу (9) Рисунок 6 – Функція розподілу інтервалів часу між викликами при
 • Щільність імовірності експоненціального розподілу описується виразом , (10) а математичне очікування й дисперсія відповідно дорівнюють , . (11) Можна показати, що розподіл інтервалів часу між викликами за експоненціальним законом є не тільки необхідною, але й достатньою умовою для того, щоб потік був найпростішим. Експоненціальний закон має таку важливу властивість: якщо проміжок часу, розподілений за експоненціальним законом, тривав певний час, то це жодним чином не впливає на закон розподілу тієї частини, що залишилася від усього проміжку.
• Щільність імовірності експоненціального розподілу описується виразом , (10) а математичне очікування й дисперсія відповідно дорівнюють , . (11) Можна показати, що розподіл інтервалів часу між викликами за експоненціальним законом є не тільки необхідною, але й достатньою умовою для того, щоб потік був найпростішим. Експоненціальний закон має таку важливу властивість: якщо проміжок часу, розподілений за експоненціальним законом, тривав певний час, то це жодним чином не впливає на закон розподілу тієї частини, що залишилася від усього проміжку.
 Нестаціонарний пуассонівський потік викликів • Нестаціонарним пуассонівським потоком (або найпростішим потоком із змінним параметром) називається ординарний потік без післядії, у якого параметр залежить від часу. Для цього потоку ймовірність надходження заявок на інтервалі часу визначається формулою , (12)
Нестаціонарний пуассонівський потік викликів • Нестаціонарним пуассонівським потоком (або найпростішим потоком із змінним параметром) називається ординарний потік без післядії, у якого параметр залежить від часу. Для цього потоку ймовірність надходження заявок на інтервалі часу визначається формулою , (12)
 Потоки з обмеженою післядією • Потоком з обмеженою післядією називається потік, у якого послідовність інтервалів часу між сусідніми викликами являє собою послідовність незалежних випадкових величин. Такий потік викликів описується послідовністю функцій розподілу інтервалів між викликами. Окремими випадками потоку з обмеженою післядією є: . - рекурентний потік, що характеризується однаково розподіленими інтервалами між викликами ; (13) - рекурентний потік із запізнюванням, для якого ; . (14)
Потоки з обмеженою післядією • Потоком з обмеженою післядією називається потік, у якого послідовність інтервалів часу між сусідніми викликами являє собою послідовність незалежних випадкових величин. Такий потік викликів описується послідовністю функцій розподілу інтервалів між викликами. Окремими випадками потоку з обмеженою післядією є: . - рекурентний потік, що характеризується однаково розподіленими інтервалами між викликами ; (13) - рекурентний потік із запізнюванням, для якого ; . (14)
 Потоки з обмеженою післядією • У теорії надійності рекурентний потік називається процесом відновлення, а рекурентний потік із запізнюванням – загальним процесом відновлення.
Потоки з обмеженою післядією • У теорії надійності рекурентний потік називається процесом відновлення, а рекурентний потік із запізнюванням – загальним процесом відновлення.
 Потоки Пальма • Стаціонарний ординарний рекурентний потік із запізнюванням називається потоком Пальма. • Потоки Пальма описують виклики, загублені в СРІ. • Найпростіший потік є особливим випадком потоку Пальма, у якого всі проміжки часу між викликами, в тому числі і перший, мають експоненціальний розподіл. • Існує теорема Пальма, яка стверджує, що якщо на СРІ із втратами та експоненціальним законом розподілу тривалості обслуговування викликів надходять виклики, що утворять потік Пальма, то потік не обслужених викликів є потоком Пальма. Зокрема, якщо вихідний потік найпростіший, то потік загублених викликів буде потоком Пальма.
Потоки Пальма • Стаціонарний ординарний рекурентний потік із запізнюванням називається потоком Пальма. • Потоки Пальма описують виклики, загублені в СРІ. • Найпростіший потік є особливим випадком потоку Пальма, у якого всі проміжки часу між викликами, в тому числі і перший, мають експоненціальний розподіл. • Існує теорема Пальма, яка стверджує, що якщо на СРІ із втратами та експоненціальним законом розподілу тривалості обслуговування викликів надходять виклики, що утворять потік Пальма, то потік не обслужених викликів є потоком Пальма. Зокрема, якщо вихідний потік найпростіший, то потік загублених викликів буде потоком Пальма.
 Потоки Пальма • У теорії випадкових потоків показується, що для потоку Пальма випадкові величини мають неперервний розподіл із щільністю ймовірності (15) де , . (16) Для потоків Пальма (17)
Потоки Пальма • У теорії випадкових потоків показується, що для потоку Пальма випадкові величини мають неперервний розподіл із щільністю ймовірності (15) де , . (16) Для потоків Пальма (17)
 Потік Ерланга • Потоком Ерланга m- го порядку називається потік Пальма, в якому інтервали між сусідніми викликами – статистично незалежні випадкові величини, розподілені за законом Ерланга m- го порядку , тобто мають неперервний розподіл із щільністю ймовірності , (18) де λ – параметр розподілу Ерланга. Потік Ерланга відноситься до класу потоків з обмеженою післядією, для яких інтервали часу між сусідніми викликами є статично незалежними випадковими величинами з довільними й у загальному випадку різними законами розподілу.
Потік Ерланга • Потоком Ерланга m- го порядку називається потік Пальма, в якому інтервали між сусідніми викликами – статистично незалежні випадкові величини, розподілені за законом Ерланга m- го порядку , тобто мають неперервний розподіл із щільністю ймовірності , (18) де λ – параметр розподілу Ерланга. Потік Ерланга відноситься до класу потоків з обмеженою післядією, для яких інтервали часу між сусідніми викликами є статично незалежними випадковими величинами з довільними й у загальному випадку різними законами розподілу.
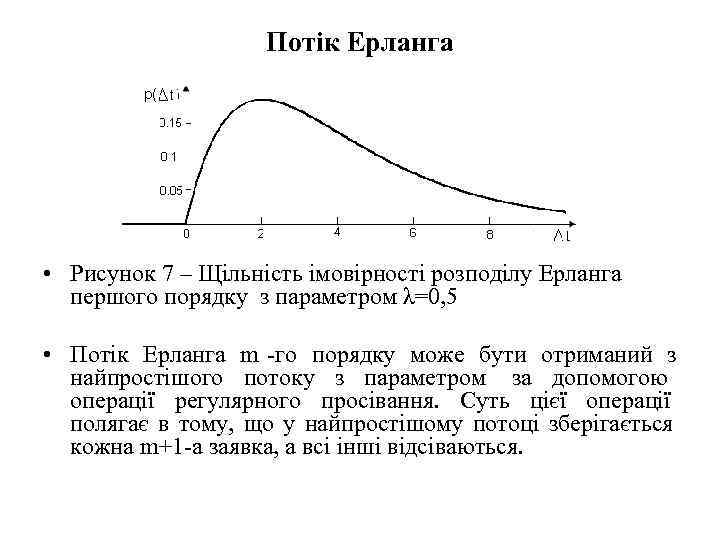
 Потік Ерланга • Рисунок 7 – Щільність імовірності розподілу Ерланга першого порядку з параметром λ=0, 5 • Потік Ерланга m -го порядку може бути отриманий з найпростішого потоку з параметром за допомогою операції регулярного просівання. Суть цієї операції полягає в тому, що у найпростішому потоці зберігається кожна m+1 -а заявка, а всі інші відсіваються.
Потік Ерланга • Рисунок 7 – Щільність імовірності розподілу Ерланга першого порядку з параметром λ=0, 5 • Потік Ерланга m -го порядку може бути отриманий з найпростішого потоку з параметром за допомогою операції регулярного просівання. Суть цієї операції полягає в тому, що у найпростішому потоці зберігається кожна m+1 -а заявка, а всі інші відсіваються.
 Потік Ерланга • При m=0 розподіл Ерланга співпадає з експоненціальним розподілом. • При m≥ 0 розподіл Ерланга має єдиний максимум у точці Δt=m/λ, тому що . (19) Математичне очікування й дисперсія інтервалу часу між сусідніми викликами в потоці Ерланга m- го порядку дорівнюють , (20) де λ – параметр розподілу.
Потік Ерланга • При m=0 розподіл Ерланга співпадає з експоненціальним розподілом. • При m≥ 0 розподіл Ерланга має єдиний максимум у точці Δt=m/λ, тому що . (19) Математичне очікування й дисперсія інтервалу часу між сусідніми викликами в потоці Ерланга m- го порядку дорівнюють , (20) де λ – параметр розподілу.
 Потік Ерланга • Потоки Ерланга при різному порядку створюють потоки з різним ступенем випадковості: від найпростішого при m=0 до детермінованого при m=∞. • Модель потоку Ерланга застосовують для опису процесів у системах розподілу інформації, коли найпростіший потік викликів розділяється на m+1 напрямок згідно з операцією регулярного просіювання.
Потік Ерланга • Потоки Ерланга при різному порядку створюють потоки з різним ступенем випадковості: від найпростішого при m=0 до детермінованого при m=∞. • Модель потоку Ерланга застосовують для опису процесів у системах розподілу інформації, коли найпростіший потік викликів розділяється на m+1 напрямок згідно з операцією регулярного просіювання.
 Потоки із простою післядією • У загальному випадку СРІ, зокрема комутаційна система (КС), впливає на процес надходження викликів (рис. 7). Рисунок 7 – Комутаційна система як СРІ • Особливо відчутний цей вплив при малій кількості джерел викликів. • Потоком з простою післядією називається ординарний потік, для якого параметр потоку залежить тільки від стану СРІ в момент часу (21)
Потоки із простою післядією • У загальному випадку СРІ, зокрема комутаційна система (КС), впливає на процес надходження викликів (рис. 7). Рисунок 7 – Комутаційна система як СРІ • Особливо відчутний цей вплив при малій кількості джерел викликів. • Потоком з простою післядією називається ординарний потік, для якого параметр потоку залежить тільки від стану СРІ в момент часу (21)
 • Сформулюємо більш строге визначення. • Потоком із простою післядією називається ординарний потік, для якого у будь-який момент часу існує кінцевий параметр потоку, що залежить від стану системи . (22) • До окремих випадків потоків із простою післядією відноситься симетричний потік, примітивний потік і потік з повторними викликами. • Стани КС, що розрізняються тільки числом зайнятих входів, називаються макростанами. • Симетричним потоком називається потік із простою післядією, параметр якого в будь-який момент часу залежить тільки від макростану системи
• Сформулюємо більш строге визначення. • Потоком із простою післядією називається ординарний потік, для якого у будь-який момент часу існує кінцевий параметр потоку, що залежить від стану системи . (22) • До окремих випадків потоків із простою післядією відноситься симетричний потік, примітивний потік і потік з повторними викликами. • Стани КС, що розрізняються тільки числом зайнятих входів, називаються макростанами. • Симетричним потоком називається потік із простою післядією, параметр якого в будь-який момент часу залежить тільки від макростану системи
 , (23) • де – число зайнятих приладів (виходів) системи у момент часу • Примітивний потік – це такий симетричний потік, у якого параметр λi прямо пропорційний числу вільних у цей момент часу джерел (24) , де – загальне число джерел викликів; – число джерел, що обслуговуються, у момент часу ; – параметр джерела у вільному стані. • Для джерел у вільному стані за звичай передбачається експоненціальний розподіл інтервалів між сусідніми викликами.
, (23) • де – число зайнятих приладів (виходів) системи у момент часу • Примітивний потік – це такий симетричний потік, у якого параметр λi прямо пропорційний числу вільних у цей момент часу джерел (24) , де – загальне число джерел викликів; – число джерел, що обслуговуються, у момент часу ; – параметр джерела у вільному стані. • Для джерел у вільному стані за звичай передбачається експоненціальний розподіл інтервалів між сусідніми викликами.
 • У телефонії примітивний потік зветься потоком ВОЧД – викликів від обмеженого числа джерел. Такий потік нестаціонарний і є потоком з післядією, оскільки ймовірність виникнення викликів залежить від числа викликів , що збільшенням і зменшенням післядія потоку зменшується. У граничному випадку , так, що модель примітивного потоку переходить у модель найпростішого потоку викликів. • Потік з повторними викликами складається з первинних викликів і повторних викликів, що надходять на СРІ повторно, якщо первинна заявка не була обслужена. У випадку найпростішого потоку первинних викликів параметр такого потоку
• У телефонії примітивний потік зветься потоком ВОЧД – викликів від обмеженого числа джерел. Такий потік нестаціонарний і є потоком з післядією, оскільки ймовірність виникнення викликів залежить від числа викликів , що збільшенням і зменшенням післядія потоку зменшується. У граничному випадку , так, що модель примітивного потоку переходить у модель найпростішого потоку викликів. • Потік з повторними викликами складається з первинних викликів і повторних викликів, що надходять на СРІ повторно, якщо первинна заявка не була обслужена. У випадку найпростішого потоку первинних викликів параметр такого потоку
 , (25) де – число джерел повторних викликів; – параметр найпростішого потоку первинних викликів.
, (25) де – число джерел повторних викликів; – параметр найпростішого потоку первинних викликів.
 Операції над потоками викликів • Основними операціями над потоками є операція об'єднання й операція просіювання. • Об'єднанням (сумою) двох потоків і називається потік , у якому моменти появи викликів складаються з моментів появи викликів у потоках і . • Два потоки називаються незалежними , якщо закон розподілу числа викликів, що потрапляють на будь-який проміжок часу в одному з потоків, не залежить від того, скільки викликів потрапило на будь-який проміжок часу в іншому потоці. При об'єднанні незалежних потоків їхні провідні функції й інтенсивності складаються.
Операції над потоками викликів • Основними операціями над потоками є операція об'єднання й операція просіювання. • Об'єднанням (сумою) двох потоків і називається потік , у якому моменти появи викликів складаються з моментів появи викликів у потоках і . • Два потоки називаються незалежними , якщо закон розподілу числа викликів, що потрапляють на будь-який проміжок часу в одному з потоків, не залежить від того, скільки викликів потрапило на будь-який проміжок часу в іншому потоці. При об'єднанні незалежних потоків їхні провідні функції й інтенсивності складаються.
 • Гранична теорема потоків свідчить: якщо підсумувати велике число ординарних незалежних потоків з близькими інтенсивностями , то сумарний потік буде близький до пуассонівського (найпростішого). Ця теорема дає теоретичне обґрунтування для широкого використання моделі найпростіших потоків. • Операція просіювання може бути як детермінована так і випадкова. Для детермінованого просіювання закон просіювання відомий і заздалегідь визначений • Операція випадкового просіювання називається рекурентною , якщо з імовірністю кожен виклик залишається в потоці, а з імовірністю втрачається. Позначається ця операція так: .
• Гранична теорема потоків свідчить: якщо підсумувати велике число ординарних незалежних потоків з близькими інтенсивностями , то сумарний потік буде близький до пуассонівського (найпростішого). Ця теорема дає теоретичне обґрунтування для широкого використання моделі найпростіших потоків. • Операція просіювання може бути як детермінована так і випадкова. Для детермінованого просіювання закон просіювання відомий і заздалегідь визначений • Операція випадкового просіювання називається рекурентною , якщо з імовірністю кожен виклик залишається в потоці, а з імовірністю втрачається. Позначається ця операція так: .
 • Якщо операції рекурентного просіювання піддати найпростіший потік з параметром , то потік буде також найпростішим з параметром , де – імовірність збереження виклику в потоці. Звідси випливає важливий для практики висновок: якщо найпростіший потік з параметром розділяється комутаційною системою на напрямків і ймовірність того, що виклик потрапить на -й напрямок, дорівнює , то потік -го напрямку також є найпростішим з параметром .
• Якщо операції рекурентного просіювання піддати найпростіший потік з параметром , то потік буде також найпростішим з параметром , де – імовірність збереження виклику в потоці. Звідси випливає важливий для практики висновок: якщо найпростіший потік з параметром розділяється комутаційною системою на напрямків і ймовірність того, що виклик потрапить на -й напрямок, дорівнює , то потік -го напрямку також є найпростішим з параметром .
 Час обслуговування викликів • Виклики, що надходять від абонентських пристроїв, займають прилади СРІ на певний час. Розрізняють математичні моделі, що відповідають фіксованому й випадковому часу обслуговування . • Фіксоване значення тривалості одного заняття припускає, що для кожного виклику визначена тривалість його обслуговування. Зокрема час може бути постійним, якщо всі виклики однакові за тривалістю обслуговування. У телефонії модель постійної тривалості обслуговування застосовується для опису роботи пристроїв керування при встановленні з'єднання. • Моделлю випадкового часу обслуговування є випадкова величина, що описується імовірнісним законом розподілу. Найпростішою і розповсюдженою моделлю
Час обслуговування викликів • Виклики, що надходять від абонентських пристроїв, займають прилади СРІ на певний час. Розрізняють математичні моделі, що відповідають фіксованому й випадковому часу обслуговування . • Фіксоване значення тривалості одного заняття припускає, що для кожного виклику визначена тривалість його обслуговування. Зокрема час може бути постійним, якщо всі виклики однакові за тривалістю обслуговування. У телефонії модель постійної тривалості обслуговування застосовується для опису роботи пристроїв керування при встановленні з'єднання. • Моделлю випадкового часу обслуговування є випадкова величина, що описується імовірнісним законом розподілу. Найпростішою і розповсюдженою моделлю
 випадкової тривалості обслуговування є випадкова величина з експоненціальним розподілом. Функція розподілу експоненціального закону має вигляд : , (26) де – параметр обслуговування. • У теорії надійності функція називається функцією надійності. Вона характеризує ймовірність того, що елемент не відмовить раніше, ніж за час . • Модель випадкової величини з експоненціальним законом розподілу використовується для опису тривалостей розмов в телефонних мережах.
випадкової тривалості обслуговування є випадкова величина з експоненціальним розподілом. Функція розподілу експоненціального закону має вигляд : , (26) де – параметр обслуговування. • У теорії надійності функція називається функцією надійності. Вона характеризує ймовірність того, що елемент не відмовить раніше, ніж за час . • Модель випадкової величини з експоненціальним законом розподілу використовується для опису тривалостей розмов в телефонних мережах.
 Потік звільнень • Потоком звільнення називається послідовність моментів закінчення обслуговування викликів. У загальному випадку властивості потоку звільнень залежать від властивостей вхідного потоку, кількості обслуговуючих приладів і закону розподілу тривалості обслуговування. • При обслуговуванні вхідного потоку викликів без втрат у випадку постійної тривалості обслуговування властивості потоку звільнень співпадають з властивостями вхідного потоку. • Виконаємо аналіз випадкової тривалості обслуговування з експоненціальним законом розподілу. • Нехай на СРІ надходить випадковий потік викликів, час заняття викликів підкоряється експоненціальному закону розподілу й обслуговування кожного виклику здійснюється незалежно.
Потік звільнень • Потоком звільнення називається послідовність моментів закінчення обслуговування викликів. У загальному випадку властивості потоку звільнень залежать від властивостей вхідного потоку, кількості обслуговуючих приладів і закону розподілу тривалості обслуговування. • При обслуговуванні вхідного потоку викликів без втрат у випадку постійної тривалості обслуговування властивості потоку звільнень співпадають з властивостями вхідного потоку. • Виконаємо аналіз випадкової тривалості обслуговування з експоненціальним законом розподілу. • Нехай на СРІ надходить випадковий потік викликів, час заняття викликів підкоряється експоненціальному закону розподілу й обслуговування кожного виклику здійснюється незалежно.
 • Покажемо, що в цьому випадку параметр потоку звільнення дорівнює , (27) де – число зайнятих виходів комутаційної системи в момент часу ; – параметр обслуговування. Якщо в СРІ у момент часу зайнято приладів, то ймовірність звільнення за час хоча б одного приладу при незалежному обслуговуванні викликів дорівнює . (28)
• Покажемо, що в цьому випадку параметр потоку звільнення дорівнює , (27) де – число зайнятих виходів комутаційної системи в момент часу ; – параметр обслуговування. Якщо в СРІ у момент часу зайнято приладів, то ймовірність звільнення за час хоча б одного приладу при незалежному обслуговуванні викликів дорівнює . (28)
 • За означенням параметра потоку . (30) • Після підстановки в ( 30 ) виразу (2 9 ) і відповідних перетворень отримаємо вираз (28). • Таким чином, параметр потоку звільнень у цьому випадку прямо пропорційний кількості обслуговуючих приладів і обернено пропорційний середньому часу обслуговування одного виклику одним приладом.
• За означенням параметра потоку . (30) • Після підстановки в ( 30 ) виразу (2 9 ) і відповідних перетворень отримаємо вираз (28). • Таким чином, параметр потоку звільнень у цьому випадку прямо пропорційний кількості обслуговуючих приладів і обернено пропорційний середньому часу обслуговування одного виклику одним приладом.
 Лекція 3 НАВАНТАЖЕННЯ І ХАРАКТЕРИСТИКИ ЯКОСТІ ОБСЛУГОВУВАННЯ ВИКЛИКІВ Основні питання 1. Поняття навантаження 2. Дисципліни обслуговування викликів 3. Характеристики якості обслуговування 4. Пропускна здатність СРІ
Лекція 3 НАВАНТАЖЕННЯ І ХАРАКТЕРИСТИКИ ЯКОСТІ ОБСЛУГОВУВАННЯ ВИКЛИКІВ Основні питання 1. Поняття навантаження 2. Дисципліни обслуговування викликів 3. Характеристики якості обслуговування 4. Пропускна здатність СРІ
 Поняття навантаження • При обслуговуванні потоків викликів у СРІ кожен з них займає обслуговуючий прилад на деякий інтервал часу. У теорії телетрафіку сумарний час зайняття приладів викликами називається навантаженням [1]. • Розрізняють навантаження, що надходить, обслуговується і втрачається. • Навантаженням, що обслуговується за інтервал часу , називається сумарний час зайняття всіх приладів СРІ , (1) де v – загальне число приладів СРІ; τi – час заняття i-го приладу за інтервал .
Поняття навантаження • При обслуговуванні потоків викликів у СРІ кожен з них займає обслуговуючий прилад на деякий інтервал часу. У теорії телетрафіку сумарний час зайняття приладів викликами називається навантаженням [1]. • Розрізняють навантаження, що надходить, обслуговується і втрачається. • Навантаженням, що обслуговується за інтервал часу , називається сумарний час зайняття всіх приладів СРІ , (1) де v – загальне число приладів СРІ; τi – час заняття i-го приладу за інтервал .
 • За одиницю виміру навантаження прийнято одне годино- заняття (1 г. -зан. ). Одне годино-заняття – це таке навантаження, що може бути обслужене одним приладом протягом години при безперервному зайнятті цього приладу. • Навантаженням Y(t 1, t 2), що надходить за інтервал часу , називається навантаження, що може бути обслужене ідеальною системою комутації, якщо кожному виклику негайно був би наданий один з обслуговуючих приладів. • Втрачене навантаження – це та частина навантаження, що надійшла і не була обслугована СРІ (2)
• За одиницю виміру навантаження прийнято одне годино- заняття (1 г. -зан. ). Одне годино-заняття – це таке навантаження, що може бути обслужене одним приладом протягом години при безперервному зайнятті цього приладу. • Навантаженням Y(t 1, t 2), що надходить за інтервал часу , називається навантаження, що може бути обслужене ідеальною системою комутації, якщо кожному виклику негайно був би наданий один з обслуговуючих приладів. • Втрачене навантаження – це та частина навантаження, що надійшла і не була обслугована СРІ (2)
 • Математичне очікування навантаження в одиницю часу (за звичай за одну годину) називається інтенсивністю навантаження. Позначається навантаження символом . При цьому говорять про інтенсивності навантажень, які надходять, обслуговуються і втрачаються. • За одиницю виміру навантаження прийнятий Ерланг. • Один Ерланг являє собою навантаження в одне годино-заняття за 1 годину. • У практиці вимірювання обслуженого навантаження використовується така теорема. • Теорема 1. Якщо на СРІ поступає стаціонарний потік викликів, то інтенсивність обслуженого навантаження, виражена в Ерлангах, кількісно дорівнює середньому числу одночасно зайнятих виходів системи, що обслуговує це навантаження.
• Математичне очікування навантаження в одиницю часу (за звичай за одну годину) називається інтенсивністю навантаження. Позначається навантаження символом . При цьому говорять про інтенсивності навантажень, які надходять, обслуговуються і втрачаються. • За одиницю виміру навантаження прийнятий Ерланг. • Один Ерланг являє собою навантаження в одне годино-заняття за 1 годину. • У практиці вимірювання обслуженого навантаження використовується така теорема. • Теорема 1. Якщо на СРІ поступає стаціонарний потік викликів, то інтенсивність обслуженого навантаження, виражена в Ерлангах, кількісно дорівнює середньому числу одночасно зайнятих виходів системи, що обслуговує це навантаження.
 • Доведення цієї теореми основується на тому, що для стаціонарних потоків викликів інтенсивність обслуженого навантаження , (3) • де Pi – імовірність заняття i-го приладу; v – загальна кількість приладів; – середнє число зайнятих виходів. • Для кількісної оцінки інтенсивності навантаження, що надходить, використовується така теорема. • Теорема 2. Інтенсивність навантаження, що створюється найпростішим потоком викликів, кількісно дорівнює математичному очікуванню числа викликів, що надходять за час, рівний середній тривалості одного заняття
• Доведення цієї теореми основується на тому, що для стаціонарних потоків викликів інтенсивність обслуженого навантаження , (3) • де Pi – імовірність заняття i-го приладу; v – загальна кількість приладів; – середнє число зайнятих виходів. • Для кількісної оцінки інтенсивності навантаження, що надходить, використовується така теорема. • Теорема 2. Інтенсивність навантаження, що створюється найпростішим потоком викликів, кількісно дорівнює математичному очікуванню числа викликів, що надходять за час, рівний середній тривалості одного заняття
 • , (4) • де і – відповідно інтенсивність і параметр потоку викликів (для найпростішого потоку ); – середній час обслуговування викликів; – інтенсивність обслуговування ( ). • Інтенсивність навантаження змінюється і залежить від сезону, дня тижня, години доби. Для забезпечення задовільної якості обслуговування абонентів у будь-який час доби розрахунок обладнання СРІ необхідно виконувати, виходячи з інтенсивності навантаження в ту годину, коли вона максимальна. Ця година називається годиною найбільшого навантаження – ГНН. Година найбільшого навантаження – це безперервний 60 -ти хвилинний інтервал часу, протягом якого середнє навантаження є максимальним.
• , (4) • де і – відповідно інтенсивність і параметр потоку викликів (для найпростішого потоку ); – середній час обслуговування викликів; – інтенсивність обслуговування ( ). • Інтенсивність навантаження змінюється і залежить від сезону, дня тижня, години доби. Для забезпечення задовільної якості обслуговування абонентів у будь-який час доби розрахунок обладнання СРІ необхідно виконувати, виходячи з інтенсивності навантаження в ту годину, коли вона максимальна. Ця година називається годиною найбільшого навантаження – ГНН. Година найбільшого навантаження – це безперервний 60 -ти хвилинний інтервал часу, протягом якого середнє навантаження є максимальним.
 Дисципліни обслуговування викликів • Всі дисципліни обслуговування викликів можна розділити на дисципліни обслуговування без втрат і дисципліни обслуговування із втратами. • Дисципліною обслуговування без втрат називається така дисципліна, при якій виклики, що надходять, негайно обслуговується. Дисципліною обслуговування із втратами – якщо виклики, що надходять, отримують відмову в обслуговуванні або їх обслуговування затримується на якийсь час. • Через економічні причини СРІ за звичай проектуються з втратами. • Розрізняють явні й умовні втрати. Дисципліною обслуговування з явними втратами називається така дисципліна, при якій виклик, отримавши відмову в обслуговуванні, залишає систему й надалі не чинить на неї жодного впливу. Дисципліною обслуговування з умовними втратами називається така, за якої виклики не втрачаються а обслуговуються з очікуванням, або ж після їх повторення.
Дисципліни обслуговування викликів • Всі дисципліни обслуговування викликів можна розділити на дисципліни обслуговування без втрат і дисципліни обслуговування із втратами. • Дисципліною обслуговування без втрат називається така дисципліна, при якій виклики, що надходять, негайно обслуговується. Дисципліною обслуговування із втратами – якщо виклики, що надходять, отримують відмову в обслуговуванні або їх обслуговування затримується на якийсь час. • Через економічні причини СРІ за звичай проектуються з втратами. • Розрізняють явні й умовні втрати. Дисципліною обслуговування з явними втратами називається така дисципліна, при якій виклик, отримавши відмову в обслуговуванні, залишає систему й надалі не чинить на неї жодного впливу. Дисципліною обслуговування з умовними втратами називається така, за якої виклики не втрачаються а обслуговуються з очікуванням, або ж після їх повторення.
 Характеристики якості обслуговування • Для оцінки якості обслуговування викликів з явними втратами використовується один з трьох видів втрат: 1) втрати викликів ; 2) втрати за часом ; 3) втрати за навантаженням . • Втрати є випадковими величинами. При розрахунках за звичай оперують їхніми середніми значеннями, тобто їхніми математичними очікуваннями. Ці середні значення називаються ймовірностями втрат. • Імовірність втрати викликів можна визначити за формулою
Характеристики якості обслуговування • Для оцінки якості обслуговування викликів з явними втратами використовується один з трьох видів втрат: 1) втрати викликів ; 2) втрати за часом ; 3) втрати за навантаженням . • Втрати є випадковими величинами. При розрахунках за звичай оперують їхніми середніми значеннями, тобто їхніми математичними очікуваннями. Ці середні значення називаються ймовірностями втрат. • Імовірність втрати викликів можна визначити за формулою
 • , (5) де – число викликів, що втрачені за розглянутий проміжок часу; – загальне число викликів. Імовірність втрат викликів можна визначити й через відношення (6) , де в чисельнику знаходиться провідна функція потоку втрачених викликів, а в знаменнику – провідна функція потоку вхідних викликів
• , (5) де – число викликів, що втрачені за розглянутий проміжок часу; – загальне число викликів. Імовірність втрат викликів можна визначити й через відношення (6) , де в чисельнику знаходиться провідна функція потоку втрачених викликів, а в знаменнику – провідна функція потоку вхідних викликів
 • Для стаціонарних потоків , де – інтенсивність потоку втрачених викликів; – інтенсивність потоку викликів, що надходять. Інакше кажучи, – частина викликів, обслуговування яких не закінчується обслуговуванням. Імовірність втрат за часом – частина часу, протягом якого виклики блокуються, тому що всі прилади зайняті обслуговуванням, тобто , де – загальне число обслуговуючих приладів, i – число зайнятих приладів.
• Для стаціонарних потоків , де – інтенсивність потоку втрачених викликів; – інтенсивність потоку викликів, що надходять. Інакше кажучи, – частина викликів, обслуговування яких не закінчується обслуговуванням. Імовірність втрат за часом – частина часу, протягом якого виклики блокуються, тому що всі прилади зайняті обслуговуванням, тобто , де – загальне число обслуговуючих приладів, i – число зайнятих приладів.
 • Імовірність втрат за навантаженням – це відношення математичного очікування навантаження, що втрачається за розглянутий проміжок часу, до математичного очікування навантаження, що надходить за той самий проміжок часу (7) • Для стаціонарних потоків (8) де – інтенсивність навантаження, що втрачається; – інтенсивність навантаження, що поступає. Величина втрат може виражатися в частках одиниці, у відсотках або в промілях. Наприклад, p=0, 005=0, 5%=5%o.
• Імовірність втрат за навантаженням – це відношення математичного очікування навантаження, що втрачається за розглянутий проміжок часу, до математичного очікування навантаження, що надходить за той самий проміжок часу (7) • Для стаціонарних потоків (8) де – інтенсивність навантаження, що втрачається; – інтенсивність навантаження, що поступає. Величина втрат може виражатися в частках одиниці, у відсотках або в промілях. Наприклад, p=0, 005=0, 5%=5%o.
 Дисципліна обслуговування з умовними втратами припускає, що виклики, які надійшли в момент зайнятості усіх приладів, не зникають, а затримуються в обслуговуванні. • За способом обслуговування затриманих викликів розрізняють: 1) обслуговування з очікуванням; 2) обслуговування з повторними викликами. • У першому випадку виклики ставляться в чергу й обслуговуються в міру звільнення приладів. У другому випадку затримані виклики повторюються через деякі проміжки часу до одержання необхідного з'єднання (активна черга). • Для оцінки якості обслуговування викликів по дисципліні з очікуванням використовуються такі характеристики.
Дисципліна обслуговування з умовними втратами припускає, що виклики, які надійшли в момент зайнятості усіх приладів, не зникають, а затримуються в обслуговуванні. • За способом обслуговування затриманих викликів розрізняють: 1) обслуговування з очікуванням; 2) обслуговування з повторними викликами. • У першому випадку виклики ставляться в чергу й обслуговуються в міру звільнення приладів. У другому випадку затримані виклики повторюються через деякі проміжки часу до одержання необхідного з'єднання (активна черга). • Для оцінки якості обслуговування викликів по дисципліні з очікуванням використовуються такі характеристики.
 • Імовірність очікування для викликів, що надходять , де kз – число затриманих викликів, а k – число що надійшли. Для стаціонарних потоків • Імовірність очікування для будь-якого виклику більше деякого часу . • Імовірність очікування затриманого виклику понад деякий час . • Середній час очікування стосовно всіх викликів • Середній час очікування стосовно затриманих викликів .
• Імовірність очікування для викликів, що надходять , де kз – число затриманих викликів, а k – число що надійшли. Для стаціонарних потоків • Імовірність очікування для будь-якого виклику більше деякого часу . • Імовірність очікування затриманого виклику понад деякий час . • Середній час очікування стосовно всіх викликів • Середній час очікування стосовно затриманих викликів .
 • Середня довжина черги • Для оцінки якості обслуговування СРІ з повторними викликами використовуються наступні характеристики: • імовірність втрат первинного виклику – ; • імовірність втрат повторного виклику – ; • середнє число повторних викликів на один первинний виклик
• Середня довжина черги • Для оцінки якості обслуговування СРІ з повторними викликами використовуються наступні характеристики: • імовірність втрат первинного виклику – ; • імовірність втрат повторного виклику – ; • середнє число повторних викликів на один первинний виклик
 Пропускна здатність СРІ • Однією з найважливіших характеристик СРІ є пропускна здатність. • Під пропускною здатністю СРІ розуміється така максимальна інтенсивність обслуженого навантаження, при якій втрати не перевищують допустимих. • У теорії телетрафіку часто використовується питома пропускна здатність як відношення пропускної здатності СРІ до числа приладів: .
Пропускна здатність СРІ • Однією з найважливіших характеристик СРІ є пропускна здатність. • Під пропускною здатністю СРІ розуміється така максимальна інтенсивність обслуженого навантаження, при якій втрати не перевищують допустимих. • У теорії телетрафіку часто використовується питома пропускна здатність як відношення пропускної здатності СРІ до числа приладів: .

