Лекція 2 ОСНОВИ ТЕОРІЇ АЛГОРИТМІВ та МАТЕМАТИЧНОЇ

Лекція № 2 ОСНОВИ ТЕОРІЇ АЛГОРИТМІВ та МАТЕМАТИЧНОЇ ЛОГІКИ Те, що я зрозумів, - прекрасно. Із цього я роблю висновок, що й те, чого я не зрозумів, також прекрасно. ( Сократ )

Інформатика за А. Самарським

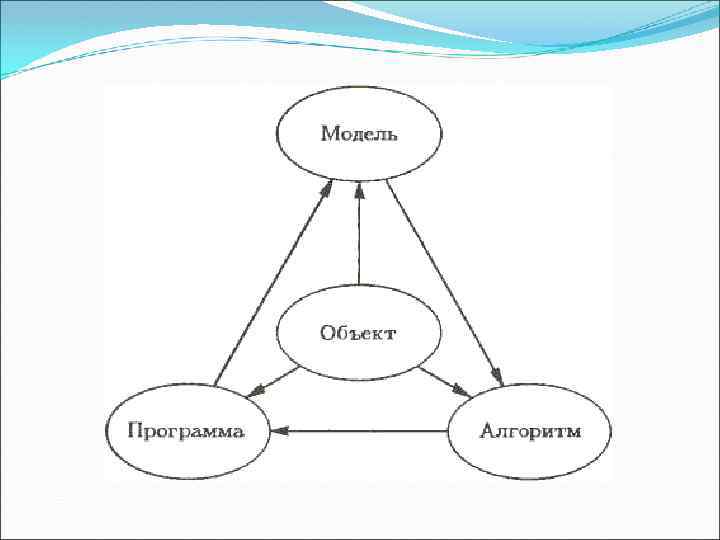
Основи ТА та МЛ Теорія алгоритмів та математична логіка Теорія множин Матлогіка Теорія графів

2. 1 Асимптотичний аналіз функцій При аналізі поводження функції трудомісткості алгоритму часто використовують прийняті в математику асимптотичні позначення, що дозволяють показати швидкість росту функції, маскуючи при цьому конкретні коефіцієнти. Така оцінка функції трудомісткості алгоритму називається складністю алгоритму й дозволяє визначити переваги у використанні того або іншого алгоритму для більших значень розмірності вихідних даних.

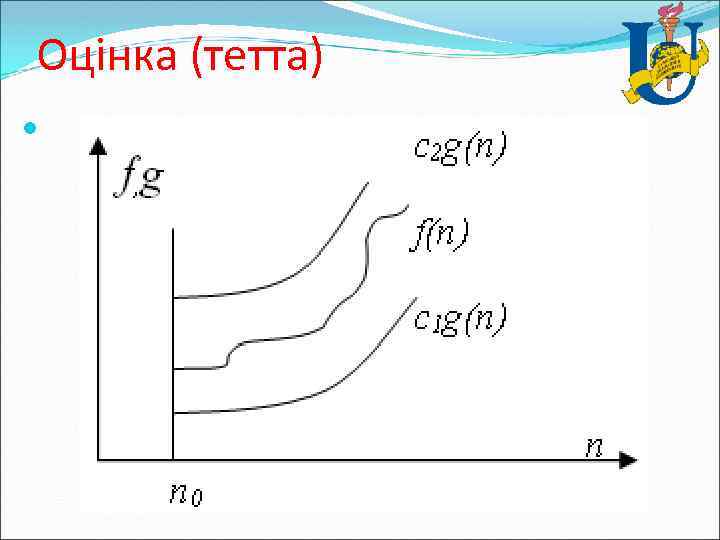
Оцінка (тетта) Нехай f(n) і g(n) - додатні функції аргументу, n ≥ 1 (кількість об'єктів на вході й кількість операцій додатні числа), тоді: f(n) = (g(n)), якщо існують такі додатні с1, с2, n 0, що: с1 * g(n) ≤ f(n) ≤ c 2 * g(n), при n > n 0

Оцінка (тетта)

Оцінка (тетта) Звичайно говорять, що при цьому функція g(n) є асимптотичною точною оцінкою функції f(n), тому що по визначенню функція f(n) не відрізняється від функції g(n) з точністю до постійного множника. Відзначимо, що з f(n) = (g(n)) слідує, що g(n) = (f(n)). Приклади: 1) f(n)=4*n 2+n*lnn+174 – f(n)= (n 2); 2) f(n)= (1) – запис означає, що f(n) або дорівнює константі, не рівної нулю, або f(n) обмежена константою на ∞: f(n) = 7+1/n = (1).

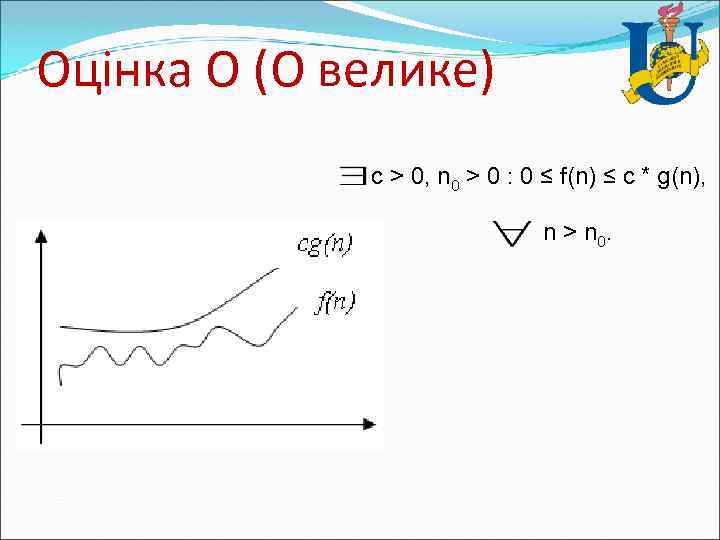Оцінка О (О велике) c > 0, n 0 > 0 : 0 ≤ f(n) ≤ c * g(n), n > n 0.

Оцінка О (О велике) Взагалі, запис O(g(n)) позначає клас функцій, таких, що всі вони ростуть не швидше, ніж функція g(n) з точністю до постійного множника, тому іноді говорять, що g(n) мажорує функцію f(n). Наприклад, для всіх функцій: f(n)=1/n, f(n)= 12, f(n)=3*n+17, f(n)=n*Ln(n), f(n)=6* n 2+24*n+77 буде справедлива оцінка О(n 2) Указуючи оцінку О є зміст указувати найбільше «близьку» мажоруючи функцію, оскільки, наприклад, для f(n)= n 2 справедлива оцінка О(n 2), однак вона не має практичного змісту.

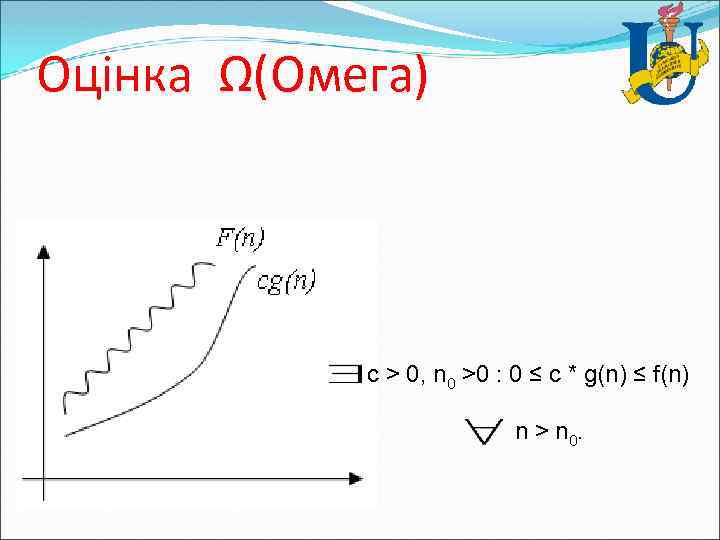Оцінка Ω(Омега) c > 0, n 0 >0 : 0 ≤ c * g(n) ≤ f(n) n > n 0.

Оцінка Ω(Омега) Наприклад, запис Ω(n*Ln(n)) позначає клас функцій, які ростуть не повільніше, ніж g(n) = n*Ln(n), у цей клас попадають всі поліноми зі ступенем більшої одиниці, так само як і всі статечні функції з підставою більшим одиниці. Асимптотичне позначення О віднесемо до підручника Бахмана по теорії простих чисел (Bachman, 1892), позначення , уведені Д. Кнутом (Donald Knuth). В асимптотичному аналізі алгоритмів розроблені спеціальні методи одержання асимптотичних оцінок, особливо для класу рекурсивних алгоритмів. Очевидно, що оцінка є більше кращої, чим оцінка О. Знання асимптотики поводження функції трудомісткості алгоритму, його складності, дає можливість робити прогнози на вибір більше раціонального з погляду трудомісткості алгоритму для великих розмірностей вихідних даних.

2. 2 Елементи теорії множин, відношення, функції і перетворення, алгебраїчні структури. Поняття множини належить до числа початкових математичних понять, воно не визначається, а поясняється тільки за допомогою прикладів. Теорія множин була створена математиками XIX століття Її сучасні положення викладені в літературі по дискретній математиці. Теорія множин була створена в роботах математиків 19 ст. Перші роботи у цій області Б. Больцано 1 (B. Bolzano), П. Дюбуа-Реймон 2 (P. Du Bois. Reymond), Р. Дедекинд 3 (R. Dedekind). Поняття множини вводиться на аксіоматичному рівні, аналогічно тому, як у математику – крапка, в інформатиці - інформація, а саме: “Множина є багато чого, мислиме як єдине”(Г. Кантор), тобто множина як «поєднання в одне ціле об'єктів, помічених нашою інтуїцією або думкою» .

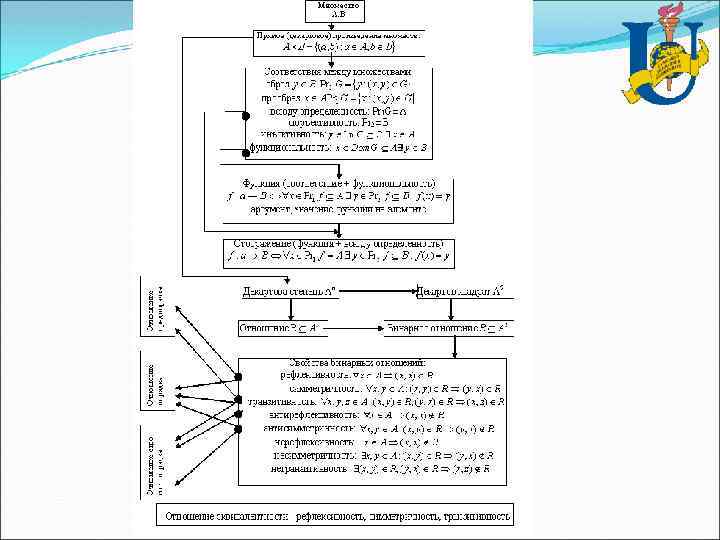
Теорія множин Нагадаємо, що при доказі тотожностей у теорії множин, діаграми Эйлера-Венна служать лише графічною ілюстрацією, а основним методом доказу є метод двох включень. Наприклад, потрібно довести, що A Δ B = (A B)/(A B). Доведемо методом двох включень. Фіксуємо довільно елемент x. Нехай x (А Δ В). Тоді, відповідно до визначення симетричної різниці х (АВ) (ВА). Це означає, що х (АВ) або х (ВА). Якщо х (АВ) , то х А и x В , тобто х (A B) і при цьому x (A B). Якщо ж х (ВА), то х B і x А, звідкіля х (A B) і при цьому x (A B). Отже, у будь-якому випадку з x (А Δ В) випливає х (A B) і x (A B), тобто x (A B)/(A B).

Скорочений запис вищенаведеного доказу з використанням логічної символіки виглядає так: Тим найперше включення, тобто включення A Δ B (A B)/(A B), установлено. Покажемо зворотне включення, тобто включення (A B)/(A B) A Δ B. Запис доказу зворотного включення з використанням логічної символіки виглядає так: Обоє включення мають місце, отже тотожність доведена.

ВІДНОШЕННЯ Серед розглянутих операцій над множинами був декартовий добуток множин А і В, що позначається через А В. Він являє собою множину {(a, b) : a A і b B}. Таким чином, множина А В складається з усіх впорядкованих пар, що мають як перший компонент елемент з множини А, а в якості другого компонента - елемент із В. ОЗНАЧЕННЯ. Відношенням R з множини А в множину В називається довільна підмножина А В. Якщо (a, b) R, це записують як a. Rb; при цьому говорять, що a і b перебувають у відношенні R, або а відноситься до b. Якщо А = В, то відношення є підмножиною А А; таке відношення називають бінарним відношенням на А.

Властивості відношень. Відношення R на А А рефлексивне, якщо (а, а) належить R для всіх а з А. Відношення R називається антирефлексивне, якщо з (a, b) R а ≠ b для всіх a, b А. Відношення R симетричне, якщо для всіх а і b, що належать А, з (а, b) R (b, a) R. Відношення R транзитивне, якщо для всіх a, b і с А з того, що (a, b) R і (b, c) R (а, с) R. Відношення R називається антисиметричним, якщо для всіх а і b з А, з приналежності (a, b) і (b, a) відношенню R a = b.

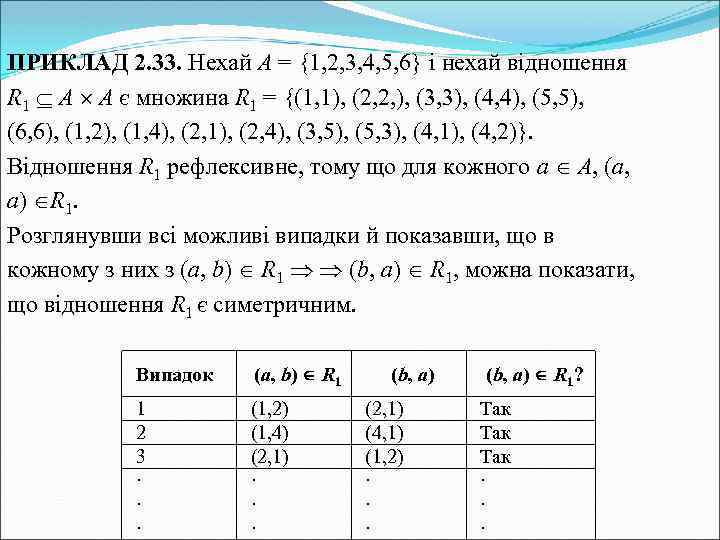ПРИКЛАД 2. 33. Нехай А = {1, 2, 3, 4, 5, 6} і нехай відношення R 1 A A є множина R 1 = {(1, 1), (2, 2, ), (3, 3), (4, 4), (5, 5), (6, 6), (1, 2), (1, 4), (2, 1), (2, 4), (3, 5), (5, 3), (4, 1), (4, 2)}. Відношення R 1 рефлексивне, тому що для кожного а А, (а, а) R 1. Розглянувши всі можливі випадки й показавши, що в кожному з них з (a, b) R 1 (b, a) R 1, можна показати, що відношення R 1 є симетричним. Випадок (a, b) R 1 1 2 3 ∙ ∙ ∙ (1, 2) (1, 4) (2, 1) ∙ ∙ ∙ (b, a) (2, 1) (4, 1) (1, 2) ∙ ∙ ∙ (b, a) R 1? Так Так ∙ ∙ ∙

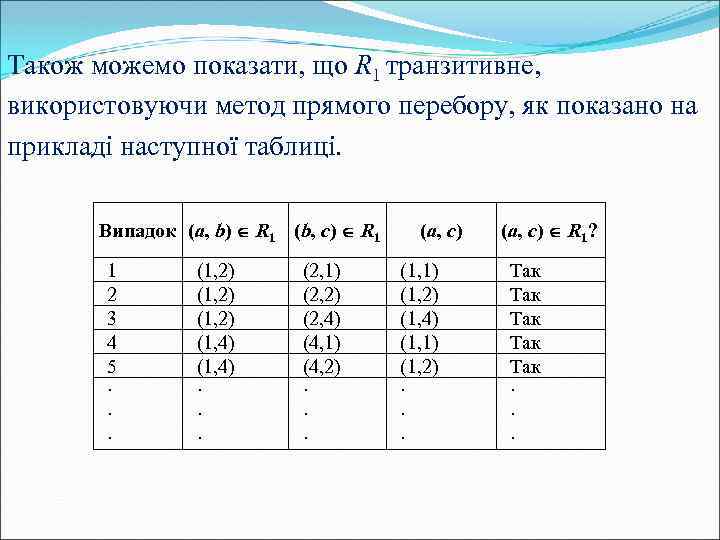Також можемо показати, що R 1 транзитивне, використовуючи метод прямого перебору, як показано на прикладі наступної таблиці. Випадок (a, b) R 1 (b, с) R 1 1 2 3 4 5 ∙ ∙ ∙ (1, 2) (1, 4) ∙ ∙ ∙ (2, 1) (2, 2) (2, 4) (4, 1) (4, 2) ∙ ∙ ∙ (а, c) (1, 1) (1, 2) (1, 4) (1, 1) (1, 2) ∙ ∙ ∙ (a, с) R 1? Так Так Так ∙ ∙ ∙