Лекция 2 Ориентация наблюдателя на Земной поверхности

1. Фигуры и модели Земли Геоид Формой Земли является геоид в переводе с греческого – «землеподобный» . – геометрическое тело, поверхность которого во всех точках перпендикулярна направлению силы тяжести.

PN отв. линия 900 E Q Рs Ру КУW α PS

a) b) c) Геоид передает действительные размеры и форму Земли. Неравномерное распределение массы Земли делает поверхность геоида нерегулярной. Такая нерегулярность имеет серьезные ограничения, как математическая модель Земли, потому что: для нее нет исчерпывающего математического выражения; небольшие изменения в форме поверхности со временим вносят небольшие ошибки в измерениях; нерегулярность поверхности делает необходимым чрезмерно большой объем вычислений

Эллипсоид вращения Для геодезических целей для изготовления карт земной поверхности и навигационных морских карт используют геометрическую форму, близкую к форме геоида и имеющую определенное математическое выражение. Эта форма – эллипсоид вращения – тело, полученное в результате вращения эллипсоида вокруг малой оси

2. Земной эллипсоид, референцэллипсоид a) b) c) d) Геоид заменяют его моделью. При этом допускаются следующие приближения: объем эллипсоида предполагается равным объему геоида; большая полуось эллипсоида а совпадает с плоскостью экватора геоида; малая полуось b направлена по оси вращения Земли, сумма квадратов уклонений поверхности эллипсоида от поверхности геоида выбирается минимальной. Такой эллипсоид называют земным эллипсоидом или земным сфероидом.

Поскольку поверхность геоида – нерегулярная, а поверхность эллипсоида – регулярная, было создано множество эллипсоидов с тем, чтобы получить лучшее соответствие геоиду для различных районов Земли. Такие эллипсоиды называются референцэллипсоиды. В разных странах приняты различные размеры земного эллипсоида, поэтому переход на иностранные карты, особенно при плавании вблизи берегов и опасностей следует осуществлять не по координатам, а по пеленгу и расстоянию ориентира, нанесенного на обе карты.

Перед использованием какого-либо эллипсоида для определения координат места необходимо определить его связь с геоидом. Датум ─ величина определяющая взаимосвязь определенного эллипсоида с геоидом. Идеальным геодезическим датумом для всемирной референцной системы является геоцентрический (его начало находится в центре массы Земли), который ориентирован через два полюса и Гринвичский меридиан. Поэтому рассматривают две группы датумов: a) местные датумы, которые базируются на удобстве и лучшей пригодности к определенному району; b) спутниковые датумы, которые используют при глобальных расчетах.

Референц-эллипсоид Красовского В Украине и России принят эллипсоид Красовского, характеризуемого следующими размерами: Большая полуось а = 6 378 245 м Малая полуось b = 6 356 863 м Среднеполярное сжатие α =1: 298, 3 Экстриситет е = 0, 0818

В 1989 году для глобальной системы позиционирования (GPS) был принят референцный датум мировых геодезических исследований WGS 84. WGS-84 – это система глобального датума, базирующегося на многих точках, определенных с большой точностью. С появлением навигационных спутниковых систем (НСС) стало необходимым и возможным создание единого земного эллипсоида. Такой эллипсоид был создан с помощью спутниковой геодезии. В настоящее время в РФ и в Украине используются «Всемирная геодезическая система» – «World Geodetic System» WGS-84 и российская система «Параметры Земли – ПЗ-90» .

Разница между длиной большой м малой полуосей земного эллипсоида невелика. Такой разницей в большинстве штурманских расчетов можно пренебречь. Поэтому в судовождении Землю принимают за шар, объемом равный объему геоида. Радиус такого шара равен 6 371 109, 7 м.

3. Системы координат, используемых в судовождении, разность широт и разность долгот 3. 1 Основные точки и линии на поверхности Земли Земная ось (axis of rotation) ─ воображаемая линия, вокруг которой происходит суточное вращение Земли. Географические или истинные полюса (geographic or true poles) ─ точки пересечения оси Земли с ее поверхностью. Полюс , откуда вращение Земли усматривается против часовой стрелки, называют северным (North Pole) и обозначают PN, а его антипод – южным (South Pole) и обозначают PS

Большие круги – линии пересечения поверхности земного сфероида плоскостями, проходящими через центр Земли. Параллели (parallels) ─ малые круги образующиеся на поверхности сфероида при пересечении его плоскостями, перпендикулярными его оси вращения. Экватор (equator) (EQ) ─ большой круг(great circle), образующийся на поверхности сфероида при пересечении его поверхности плоскостью проходящей через центр Земли и перпендикулярной ее оси вращения. Географические , или истинные меридианы (geographic or true meridians) ─ следы пересечения сфероида плоскостями, проходящими через ось вращения Земли.

Меридиан наблюдателя (observer’s meridian) ─ меридиан, проходящий через точку наблюдателя, Нулевой меридиан ─ меридиан, проходящий через пассажный прибор в Гринвичской обсерватории вблизи Лондона. Нулевой меридиан чаще называют Гринвичским. Отвесная линия или вертикаль ─ прямая, совпадающая с направлением силы тяжести в точке наблюдения. Соответствующие плоскости называют: плоскость параллели, плоскость экватора и плоскость истинного меридиана.

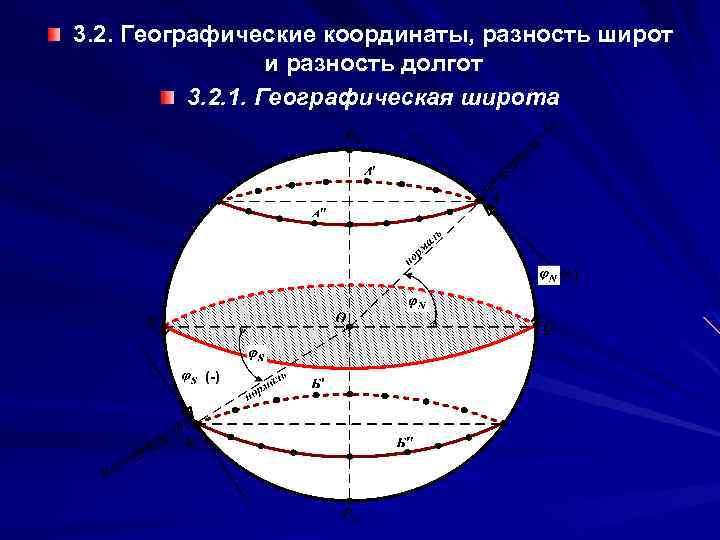
3. 2. Географические координаты, разность широт и разность долгот 3. 2. 1. Географическая широта

Географическая широта (φ) точки (latitude) – это угол с вершиной в центре Земли между отвесной линией, проходящей через данную точку, и плоскость земного экватора. Широта измеряется дугой меридиана от экватора до параллели данной точки от 0° (на экваторе) до 90° (на полюсе). Если точка находится в северном полушарии, то широте приписывается наименование N, если в южном, то S. Северная широта имеет условный знак «+» , а южная «–»

3. 2. 2. Географическая долгота

Географическая долгота (λ) места (longitude)– это двугранный угол между плоскостями Гринвичского меридиана и меридиана данной точки Долгота измеряется дугой экватора от Гринвичского меридиана до меридиана точки от 0° до 180° в сторону оста или веста. Если точка находится в восточном полушарии, ей присваивается наименование E, а если в западном W. Остовая долгота имеет условный знак «+» , а вестовая знак – «–» . Полюса являются особыми точками, где долгота не определена. Широта и долгота измеряются в градусах, минутах и их долях.

Для построения карт для районов высоких широт применяется квазигеографическая система координат. нулевой меридиан квазімеридіан PN λq φq квазиэк ватор квазіпа ралель Pq. N А квазимеридиа аанан Pq. S PS Рис. 4

В этой системе координат квазиполюсы Рq. N, Pq. S сдвинуты относительно географических полюсов на 90°. Координатные оси – квазиэкватор (меридиан 90°Е – 90° W); - начальный (нулевой) квазимеридиан (меридиан 0° – 180°). Координатные линии: – квазимеридиан; - квазипараллель. Координаты: квазиширота (φq); квазидолгота (λq)

В полярной системе координат место точки на поверхности Земли определяется по направлению и расстоянию относительно исходной точки. Как правило, эта система используется при определении положения судна относительно другого объекта или наоборот.

Разность широт и разность долгот Разность широт (РШ)(difference of latitudes) двух точек – это меньшая из дуг любого меридиана, заключенная между параллелями этих точек.

Разность широт (РШ) (Δφ)(difference of latitudes) двух точек – это меньшая из дуг любого меридиана, заключенная между параллелями этих точек. РШ или Δφ измеряется от 0° до 180° и имеет наименование «к N» , если северная широта увеличивается, а южная уменьшается, или «к S» , если северная широта уменьшается, а южная увеличивается. Δφ = φ2 – φ1 (2. 1) Разность широт «к N» имеет знак «плюс» , Разность широт «к S» имеет знак «минус»

Разность долгот (РД) (difference of longitudes) двух точек – это меньшая из дуг экватора, заключенная между меридианами этих точек. РД или Δλ измеряется от 0° до 180° и имеет наименование «к E» , если восточная долгота увеличивается или западная уменьшается, или «к W» , если западная долгота увеличивается или восточная уменьшается. Δλ = λ 2 – λ 1 (2. 2) Разность долгот «к E» имеет знак «плюс» , Разность долгот «к W» имеет знак «минус» Если в расчетах разность долгот более 180°, то необходимо взять его дополнение до 360° и сменить наименование.

3. 3. Ортодромия Кратчайшим расстоянием на шаре между двумя точками является дуга большого круга (ДБК), называемая ортодромией (great circle). В переводе с греческого языка ортос – прямой, дромос – проход, бег. Ортодромия пересекает меридианы под разными углами. Поэтому, при плавании по ортодромии приходится постоянно менять курс судна. Вертекс ─ точка максимальной широты дуги большого круга (ДБК).

Свойства ортодромии: 1. Меридиан вертекса является осью симметрии ортодромии, т. е. ортодромия дважды пересекает каждый меридиан. 2. Если угол между меридианом и ортодромией А, то при А 0 = 90°(270°) ортодромия совпадает с экватором, при А 0 = 0°(180°) ортодромия совпадает с меридианом. 3. Ортодромия пересекает каждый меридиан в одной и той же точке. 4. Ортодромия пересекает все меридианы под различными углами.

3. 4. Локсодромия Прямая, пересекающая меридианы под одним углом называется локсодромией (loxodromec or Rhumb line). В переводе с греческого языка локсос – косой, дромос – проход, бег. Так как меридианы не параллельны, то и локсодромия, пересекающая их под равными углами К не прямая линия. Она представляет собой логарифмическую спираль – линию двоякой кривизны, которая стремится к полюсу.

1. 2. 3. Свойства локсодромии: При К = 0°(180°) локсодромия совпадает с меридианом; При К= 90°(270°) локсодромия совпадает с параллелью. В частном случае при φ2= φ1=0 о локсодромия совпадает с экватором; Локсодромия пересекает каждый меридиан бесчисленное количество раз, но каждый раз в новой широте.

3. 5. Ортодромическая поправка В практике судовождения возникает необходимость перехода от ортодромических направлений к локсодромическим и наоборот. Угол между ортодромией и локсодромией, проходящими через две заданные точки называется ортодромической поправкой ψ.

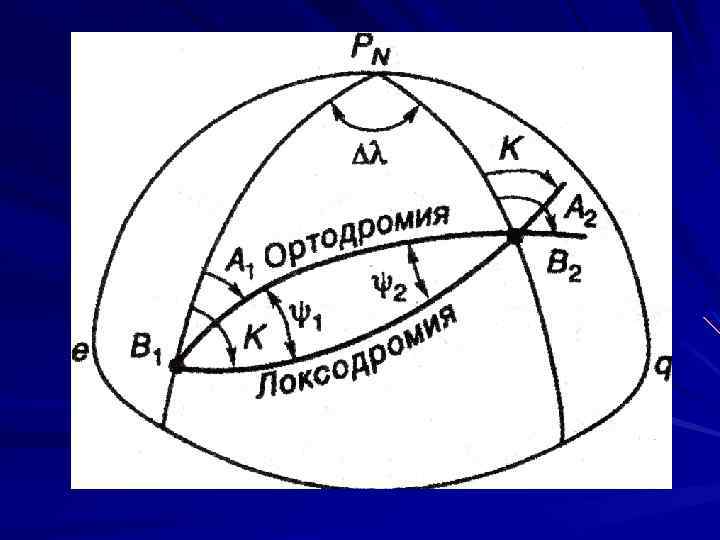
На расстоянии до 500 миль можно считать ортодромию и локсодромию расположенными симметрично, и тогда ψ 1 = ψ2 = ψ. Если расстояние между точками В 1 и В 2 больше 500 миль, то ψ1≠ψ2 В этом случае необходим непосредственный расчет ортодромической поправки как разности направлений локсодромии и ортодромии по формуле: Ψ = К – А (2. 3) Для облегчения расчета ортодромической поправки на малых расстояниях расчет производится с помощью Мореходных таблиц.

1. 2. 3. Выводы: Из-за сложности геометрии геоида, затрудняющей решение навигационных задач, для решения задач навигации используют эллипсоид вращения – тело, полученное в результате вращения эллипсоида вокруг малой оси. Для картографических и геодезических расчетов в определенных районах земли необходимо иметь эллипсоид, поверхность которого максимально совпадала с поверхностью данного района. Это референц-эллипсоид. Очевидно, что в конкретном районе это будет различный референц-эллипсоид. Для решения специальных навигационных задач, например задач определения места судна с помощью глобальных навигационных систем, применяются специальные, международные референц-эллипсоиды WGS-72 и WGS-84.

4. 5. Положение какой-либо точки на поверхности Земли определяются географическими координатами широтой (Latitude) и долготой (Longitude). Разница в координатах двух точек определяется разностью широт и разностью долгот.

Контрольные вопросы 1. Какова реальная форма Земли? 2. Какие ограничения накладывает нерегулярность поверхности геоида? 3. Что такое земной эллипсоид? 4. Что такое референц-эллипсоид? 5. Что такое земная ось? 6. Что такое географические или истинные полюса? 7. Что такое большой круг? 8. Что такое параллель? 9. Что такое экватор? 10. Что такое географический, или истинный меридиан? 11. Что такое меридиан наблюдателя? 12. Что такое нулевой меридиан?

13. 14. 15. 16. 17. 18. 19. 20. Что такое отвесная линия? Что такое географическая широта? Что такое географическая долгота? Что такое разность широт (РШ)? Что такое разность долгот (РД)? Что такое ортодромия? Что такое локсодромия? Что такое ортодромическая поправка?