ЛЕКЦИЯ 2 ОПТИМИЗАЦИОННЫЕ ЭКОНОМИКОМАТЕМАТИЧКСКИЕ МОДЕЛИ ПЛАН 2

ЛЕКЦИЯ 2 ОПТИМИЗАЦИОННЫЕ ЭКОНОМИКОМАТЕМАТИЧКСКИЕ МОДЕЛИ

ПЛАН 2. 1 Постановка задачи экономикоматематического моделирования. 2. 2 Примеры задач экономикоматематического моделирования (самостоятельная работа). 2. 2. 1 Задача определения оптимального плана производства. 2. 2. 2 Задача о «диете» . 2. 2. 3 Транспортная задача.

Целевая функция, или функция цели F = f (x 1, x 2, . . . , xn; y 1, y 2, . . . , ym; c 1, c 2, . . . , cl) (2. 1) В общем виде задача экономико- математи-ческого моделирования формулируется так: Найти такие значения управляемых переменных xj, чтобы целевая функция достигала экстремального (максимального или минимального значения). (2. 2)

Система ограничений или система условий задачи (2. 3) (2. 4) Зависимости (2. 2)—(2. 4) образуют экономико -математическую модель экономической системы.

1. 2. 3. 4. Модель должна адекватно описывать реальные технологические и экономические процессы. В модели необходимо учитывать все значимое, существенное в исследуемом явлении или процессе, пренебрегая всем второстепенным, несущественным в нем. Модель должна быть понятной для пользователя, удобной для реализации на ЭВМ. Необходимо, чтобы множество переменных xj было не пустым.

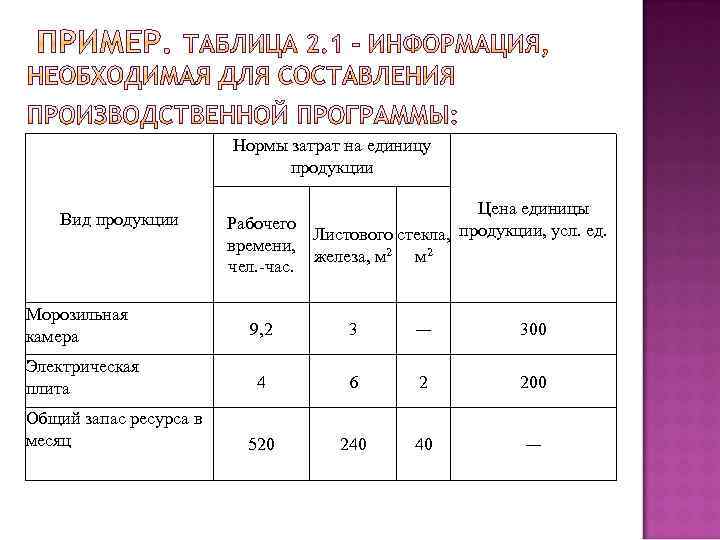Нормы затрат на единицу продукции Вид продукции Морозильная камера Электрическая плита Общий запас ресурса в месяц Цена единицы Рабочего Листового стекла, продукции, усл. ед. времени, железа, м 2 чел. -час. 9, 2 3 — 300 4 6 2 200 520 240 40 —

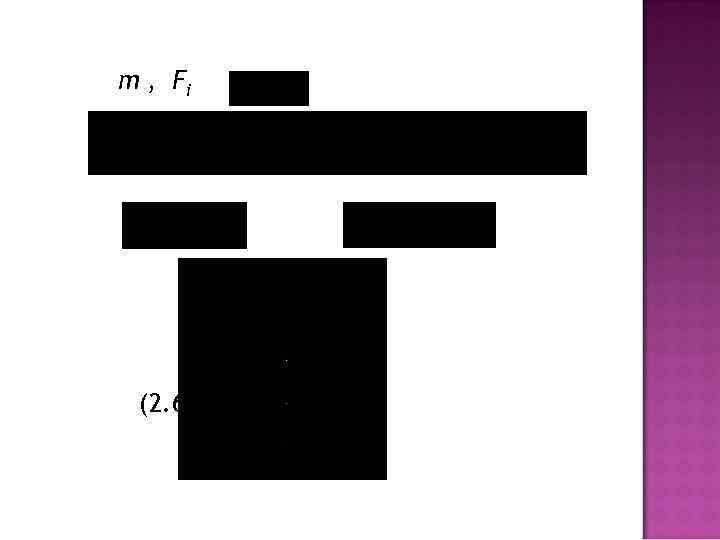m , Fi (2. 5) (2. 6)

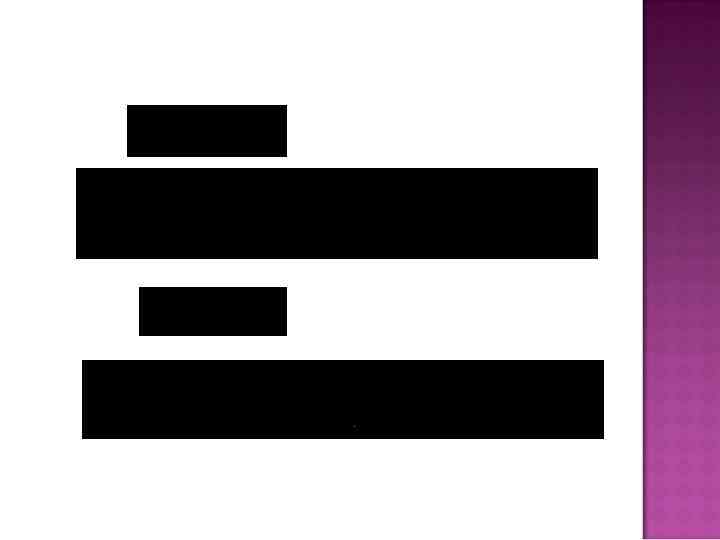(2. 7) (2. 8)

Математическое программирование — одно из направлений прикладной математики, предметом которого являются задачи для нахождения экстремума некоторой функции при заданных условиях.