4th year lect2r.ppt
- Количество слайдов: 43

Лекция 2. Напоминание Формула Дебая Комптона: Фотон – частица ! Из релятивистских законов сохранения энергии и импульса Учли квантовую ! связь импульса с длиной волны k= 2 ħ/ , получили известную квантовую формулу Дебая Комптона: Эта формула (и сам эффект комптоновского смещения частоты) является существенно квантовой. В классическом пределе ħ 0 изменение длины волны фотона при рассеянии исчезает, что и имеет место в классической электродинамике – комптоновская длина волны частицы 1

Магнитный момент нейтрона • Гипотеза о наличии у нейтрона магнитного момента возникла 1934 году, когда развитая О. Штерном с сотрудниками техника измерения магнитных моментов молекул за счет отклонения молекулярного пучка в неоднородноммагнитном поле (опыты Штерна - Герлаха) позволила измерить магнитные моменты протона и дейтона. • Оказалось, что они существенно различны. • В работе Эстермана и Штерна (апрель 1934 г. ) была высказана мысль, что магнитный момент дейтона должен быть равен сумме магнитных моментов составляющих его протона и нейтрона и дана оценка на величину магнитного момента нейтрона µn в 1, 5 - 2 ядерных магнетона µN (прямое доказательство существования магнитного момента нейтрона путем его непосредственного измерения было получено лишь в 1940 г. в опытах Альвареца и Блоха, которые получили величину µn =(-1, 935 0, 030) µN. • Почти одновременно и, несомненно, независимо в ДАН СССР появилась работа И. Е. Тамма и С. А. Альтшуллера. Анализируя данные о магнитных моментах ядер, известные из спектроскопических работ по сверхтонкому расщеплению, Тамм и Альтшуллер также пришли к выводу о существовании у нейтрона отрицательного магнитного момента, имеющего величину порядка 0, 5 я. м. 2

Магнитный момент нейтрона Что такое ядерный магнетон? Из уравнения Дирака (написанного им в 1928 г. ) следует, что любая "элементарная" частица с зарядом e, спином ½ и массой m обладает магнитным моментом Этот дираковский магнитный момент для электрона совпадает с магнетоном Бора µB, а для протона называется ядерным магнетоном: Заметим, что опять возникла знакомая нам комптоновская длина волны частицы. Таким образом, в теории Дирака, если измерять магнитные моменты в ядерных магнетонах, магнитный момент протона µp=1, а нейтрона µn = 0. Однако из эксперимента следует, что у нейтрона µn= -1, 9, а у протона µp = 2, 8. 3

Магнитный момент нейтрона Отличие магнитного момента от дираковского называется аномальным магнитным моментом: µ = µ - µD. То есть магнитный момент нейтрона целиком аномален. Кроме того, нетрудно заметить, что аномальные магнитные моменты протона и нейтрона приблизительно равны, но противоположны по знаку: µ n= -1, 9, µ p = + 1, 8. Это говорит о достаточно сложной структуре нуклонов (в этом смыслеони не элементарны). С точки зрения мезонной теории ядерных сил, нуклоны непрерывно испускают и поглощают -мезоны т. е. они окружены мезонным облаком, а поскольку протон и нейтрон испускают -мезоны разных знаков, то, в принципе, можно понять разный знак и приблизительное равенство аномальных моментов по величине. 4

Магнитный момент нейтрона Размер этого облака (а следовательно, и нуклона) можно оценить из простых соображений, пользуясь соотношением неопределенностей. Самопроизвольное рождение -мезона (или другой частицы) нарушает закон сохранения энергии по крайней мере на величину энергии покоя mc 2. Из соотношения неопределенностей следует, что такое нарушение может произойти лишь на время t ħ/mc 2, за это время -мезон может улететь от нуклона на расстояние не большее c t, Таким образом, размер r. N нуклона (размер мезонного облака) есть: r. N = c t = ħ/m c = с /2 Этот результат есть следствие теории относительности (связь массы и энергии) и квантовой механики (соотношение неопределенностей). Он имеет общий и глубокий смысл, а именно: в релятивистской квантовой теории число частиц в принципе не сохраняется, одни частицы могут исчезать, а другие появляться. Поэтому такая теория должна естественным образом описывать рождение и уничтожение частиц, в частности, процессы распада 5 элементарных частиц
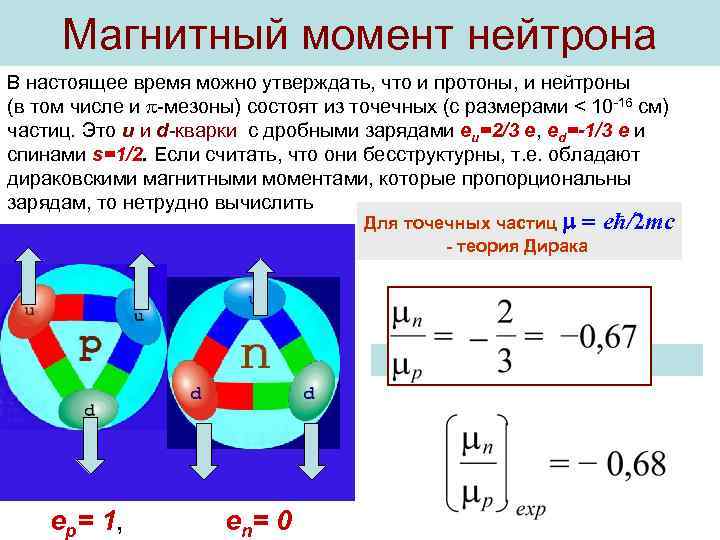
Магнитный момент нейтрона В настоящее время можно утверждать, что и протоны, и нейтроны (в том числе и -мезоны) состоят из точечных (с размерами < 10 -16 см) частиц. Это u и d-кварки с дробными зарядами eu=2/3 e, ed=-1/3 e и спинами s=1/2. Если считать, что они бесструктурны, т. е. обладают дираковскими магнитными моментами, которые пропорциональны зарядам, то нетрудно вычислить Для точечных частиц - теория Дирака ep= 1, en= 0 eħ/2 mc
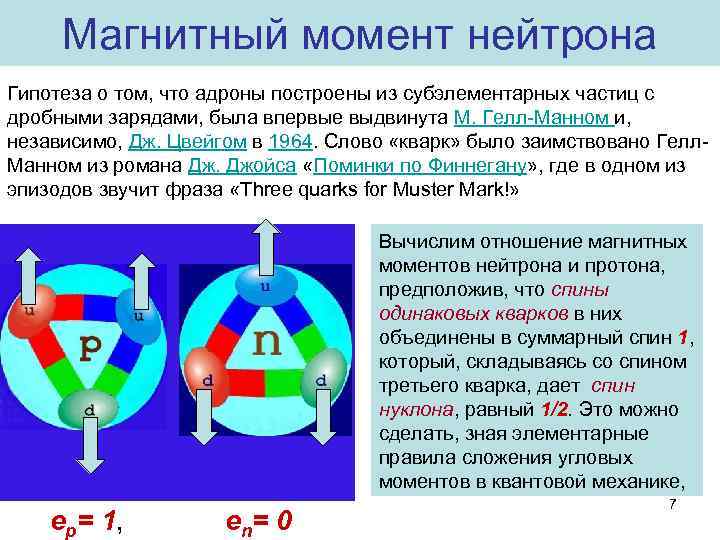
Магнитный момент нейтрона Гипотеза о том, что адроны построены из субэлементарных частиц с дробными зарядами, была впервые выдвинута М. Гелл-Манном и, независимо, Дж. Цвейгом в 1964. Слово «кварк» было заимствовано Гелл. Манном из романа Дж. Джойса «Поминки по Финнегану» , где в одном из эпизодов звучит фраза «Three quarks for Muster Mark!» Вычислим отношение магнитных моментов нейтрона и протона, предположив, что спины одинаковых кварков в них объединены в суммарный спин 1, который, складываясь со спином третьего кварка, дает спин нуклона, равный 1/2. Это можно сделать, зная элементарные правила сложения угловых моментов в квантовой механике, ep= 1, en= 0 7

Магнитный момент нейтрона Обозначим и - волновые функции двухкварковых систем с угловым моментом 1 и проекцией на ось квантования =-1, 0, 1. Волновую функцию одиночных u и d-кварков со спином 1/2 и проекцией ( = 1/2, 1/2) запишем в виде и , тогда для нейтрона В результате, магнитный момент нейтрона: 8
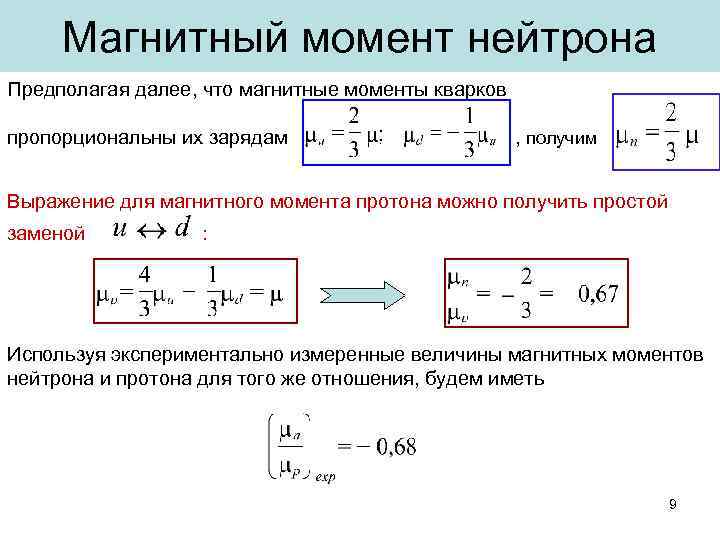
Магнитный момент нейтрона Предполагая далее, что магнитные моменты кварков пропорциональны их зарядам , получим Выражение для магнитного момента протона можно получить простой заменой : Используя экспериментально измеренные величины магнитных моментов нейтрона и протона для того же отношения, будем иметь 9

Магнитный момент нейтрона • Таким образом, простая гипотеза о кварковом составе нуклонов и простые рассуждения привели к результату, прекрасно согласующемуся с экспериментальными данными. Из этого примера также видно, как электромагнитные свойства нейтрона могут быть связаны с гораздо более глубоким строением элементарных частиц. • Наши рассуждения можно продолжить. Например, мы подтвердили наше предположение, что спины одинаковых кварков в нуклоне параллельны, но оно противоречит принципу Паули. • Кроме того, была открыта частица ++ барион с зарядом +2 и спином 3/2, т. е. состоящая из 3 -х одинаковых кварков с одинаковыми спинами • Выход из ситуации предложили: советские физики Н. Н. Боголюбов, Б. В. Струминский, А. Н. Тавхелидзе и японский физик Ёитиро Намбу. Принцип Паули не нарушится, если считать, что u-кварки отличаются друг от друга значением еще одного квантового числа, способного принимать три (и только три) разных значения. Намбу предложил название цвет, поскольку все богатство красок окружающего мира получается из трех основных цветов. 10

О природе ядерных сил • Как и чем удерживаются нуклоны в ядре, несмотря на сильное кулоновское расталкивание протонов? • Ясно, что должно быть взаимодействие более сильное, чем кулоновское, и кроме того гораздо более короткодействующее. • Юкава, развивая идеи И. Е. Тамма и Д. Д. Иваненко о возможности взаимодействия за счет обмена частицами, предположил в 1934 году, что таким может быть взаимодействие, обусловленное обменом частицей – мезоном (с промежуточной межуду электроном и протоном массой), и получил вид потенциала взаимодействия. Эта гипотеза блестяще подтвердилась: через некоторое время в 1947 г. такие частицы -мезоны были обнаружены (следует отметить, что сначала в качестве кандидата в "переносчики" ядерного взаимодействия рассматривался открытый в 1937 г. также в космических лучах мюон, называемый раньше мю-мезоном).

О природе ядерных сил. Двухуровневые системы • Поясним, что понимается под "обменом", как за его счет можно получить взаимодействие и какой вид оно будет иметь. • Рассмотрим, например, молекулярный ион водорода, т. е. два протона и электрон, который их связывает.

Когда протоны далеко друг от друга, имеются два состояния: |1 электрон связан с первым протоном и |2 электрон связан со вторым протоном Энергии этих состояний обозначим E 1 и E 2 (в нашем случае эти энергии одинаковы), так что можно написать:

О природе ядерных сил • Здесь H 0 гамильтониан системы при большом расстоянии между протонами. • Что произойдет, если мы будем сближать протоны? • Появляется вероятность того, что за счет туннельного эффекта электрон от одного протона перейдет к другому, т. е. возникает некая добавка V к гамильтониану H 0, которая приводит к переходам из первого состояния во второе и наоборот |1 |2. • В результате нужно решать уравнение Шредингера с учетом этой добавки:

О природе ядерных сил Будем искать решение в виде Для коэффициентов (a 1, a 2) получим уравнение Шредингера в матричном виде: Здесь мы приняли, что взаимодействие V приводит только к перемешиванию состояний 1 и 2, но не изменяет их энергию, т. е. m|V|m = 0.

О природе ядерных сил Условие разрешимости этой однородной системы уравнений (секулярное уравнение) определяет новые энергии нашей двухуровневой системы с учетом добавочного взаимодействия, обусловленного туннельными переходами. Если состояния вырождены, т. е. E 1=E 2= (наш случай)

О природе ядерных сил В этом случае из уравнений следует ! Это означает, что для вырожденных состояний сколь угодно малое возмущение их полностью перемешивает: возникают симметричная и антисимметричная комбинации этих состояний с разными энергиями ("отталкивание" уровней при пересечении). Эта разница возрастает с уменьшением расстояния, поскольку при этом растет вероятность туннелирования электрона.

О природе ядерных сил Таким образом, например, если энергия симметричного состояния уменьшается, то можно сказать возникает добавочное притяжение между протонами, которое и уменьшает энергию системы при сближении (в квантовой химии такое состояние имеет название: связующая орбиталь. Физический смысл возникновения притяжения также понятен: для симметричного состояния электрон концентрируется в основном между протонами, чем и уменьшает их отталкивание. Аналогично антисимметричное состояние (разрыхляющаяорбиталь), для которого электрон концентрируется за протонами, имеет более высокую энергию, что эквивалентно добавочному отталкиванию протонов.

О природе ядерных сил Это добавочное отталкивание или притяжение определяются величиной |V 12|, которую просто оценить из следующих соображений. Эта величина пропорциональна амплитуде вероятности найти электрон у второго протона на расстоянии R от первого при условии, что он связан с первым протоном. А это есть не что иное, как просто значение волновой функции электрона, связанного в яме (первый протон), в области за ямой на расстоянии R, во второй яме (второй протон) Заметим, что =1/a, где а – боровский радиус

О природе ядерных сил Таким образом, из-за обмена электроном возникает дополнительное короткодействующее взаимодействие. Именно такой потенциал получил Юкава, предположив, что два нуклона обмениваются не реальной подбарьерной частицей, а виртуальным -мезоном, т. е. реально не существующим. Что бы это могло значить? А то, что высота барьера (а точнее, энергия связи) равна всей массе -мезона. Другими словами, вблизи одного из нуклонов появляется -мезон с нулевой полной энергией E (с энергетической точки зрения ничего не появляется) и поглощается вторым нуклоном.

О природе ядерных сил Из равенства нулю энергии -мезона следует (как и в случае подбарьерного электрона) мнимость импульса Т. е. амплитуда вероятности найти -мезон у второго нуклона и, соответственно, взаимодействие между нуклонами, обусловленное обменом такого рода виртуальным -мезоном, будет иметь вид

О природе ядерных сил Это и есть потенциал Юкавы. Радиус действия ядерных сил определяется комптоновской длиной волны -мезона и имеет порядок 10 -13 см, эта величина является единицей измерения длины в ядерной физике и носит название ферми (Фм). Если массу частицы "переносчика" взаимодействия положить равной нулю, получим закон Кулона. Кулоновское взаимодействие и возникает в результате обмена заряженных частиц безмассовыми фотонами.

О природе ядерных сил Заметим, что константа g с размерностью заряда характеризует амплитуду рождения -мезона нуклоном (плотность мезонного облака вокруг нуклона или силу взаимодействия между нуклонами) так же, как заряд частицы - амплитуду излучения виртуальных фотонов (величину электрического поля). Виртуальные частицы (при выполнении законов сохранения энергии и импульса) могут превращаться в реальные, и тогда эти константы будут характеризовать уже амплитуды реальных процессов с участием -мезонов или фотонов. Обезразмеренная константа g 2/ħc, имеет величину порядка единицы, поэтому взаимодействие называется сильным (для электромагнитного взаимодействия ту же роль играет постоянная тонкой структуры =e 2/ ħc, которая равна 1/137. С большой величиной константы g связаны трудности в описании сильного взаимодействия в рамках мезонной теории, в частности, неприменима теория возмущений, которая привела к замечательным результатам в квантовой электродинамике.

Рассеяние нейтрона изолированным ядром Мы выяснили, что радиус действия ядерных сил определяется комптоновской длинойволны -мезона А поскольку длины волн тепловых нейтронов при рассеянии на ядрах они не будут "чувствовать" форму потенциала, то есть в этом случае рассеяние практически не будет отличаться от рассеянияна точечном объекте.

Рассеяние нейтрона изолированным ядром Это задача двух тел. Она сводится к задаче о рассеянии частицы с приведенной массой m на неподвижном силовом центре V(r). Вне области действия сил волновая функция нейтрона с энергией E и импульсом ħka - плоская волна

Плоская волна нормирована на 1 частицу в единицу объема, или, что то же самое, так, чтобы плотность потока частиц равнялась скорости va Это выражение имеет простой физический смысл числа частиц, которые пересекут единичную площадку за единицу времени (это все частицы, находящиеся на расстоянии < v от площадки), т. е. j = va , при =1 j = va

Итак, пусть на ядро падают частицы с плотностью потока ja. В результате взаимодействия происходит их рассеяние. Для решения задачи о рассеянии, нужно решить уравнение Шредингера, которое удобно записать в следующем виде: Решения, представляющие суперпозицию плоской волны и рассеянных волн, можно получить при помощи свободной функции Грина G(r, r'), которая описывает распространение частиц от точечного источника, расположенного в точке r'. Она удовлетворяет уравнению Общее решение У. Ш. можно представить как суперпозицию падающей волны и суммы волн, исходящих от точечных источников, распределенных в соответствии с правой частью

Это выражение представляет собой аналог известного в оптике принципа Гюйгенса. Каждая точка r' рассеивателя, куда попадает волна, становится источником новой сферической волны с амплитудой, определяемой величиной потенциала в этой точке Функция Грина, соответствующая уходящим (рассеянным) волнам, представляет собой сферическую волну, расходящуюся от источника

Поместив источник в начало координат, для радиальной компоненты плотности тока jr получим Из последнего выражения следует, что число нейтронов, проходящих в единицу времени через сферу площадью 4 r 2, окружающую источник, есть v/4. Это означает, что мощность источника в виде -функции соответствует рождению v/4 нейтронов в единицу времени. Таким образом, в. ф. имеет вид Каков ее вид на больших расстояниях при | r | >> | r‘ | ?

В этом случае ( | r | >> | r‘ | ) В итоге, в. ф. (на больших по сравнению с размерами ядра Расстояниях) можно представить в виде суммы падающей и сферической, расходящейся от центра рассеянной волны

Величина Aba называется амплитудой рассеяния. При | r | >> | r‘ | она определяет амплитуду рассеянной сферической волны Через элемент площадки r 2 d в одну секунду проходит d. N = jr r 2 d рассеянных частиц, где jr радиальная плотность потока Отношение d. N к плотности падающего потока – дифференциальное сечение рассеяния

Сечение рассеяния имеет смысл площадки, расположенной перпендикулярно пучку, которая рассеивает с единичной вероятностью (в классической механике это – площадь поперечного сечения рассеивателя) Решая интегральное уравнение для a методом последовательных приближений, получим Соответственно, для амплитуды рассеяния

Этому ряду теории возмущений для амплитуды рассеяния можно сопоставить ряд графиков (диаграмм), которые имеют довольно наглядный смысл. Это – амплитуды рассеяния, получающиеся в результате однократного, двукратного и т. д. взаимодействия частицы с силовым центром

В первом борновском приближении (или просто в борновском) получим следующее выражение для амплитуды рассеяния: – переданный импульс от рассеивателя частице.

Так что, в борновском приближении амплитуда рассеяния с передачей импульса q определяестся соответствующей фурье-компонентой потенциала соответственно, сечение

Рассеяние частиц при столкновении также можно рассматривать как квантовый переход между состояниями непрерывного спектраиз состояния exp (kar) в состояние exp (kbr) Под действием возмущения V(r). Скорость перехода (вероятность в единицу времени) дается "золотым" правилом Ферми: Интегрируя по энергии при помощи -функции, будем иметь

Метод парциальных волн в теории рассеяния Возможность использования теории возмущений определяется достаточной малостью потенциала взаимодейстаия, по сравнению с энергией налетающей частицы. В области же достаточно малых энергий (больших длин волн) налетающих частиц имеется другая возможность упростить задачу о рассеянии, используя в качестве малого параметра отношение радиуса действия ядерных сил к длине волны частицы. Проиллюстрируем это в теории возмущений Когда длина волны a=1/ka >> RN (RN –радиус действия сил), то qr << 1, и экспоненту можно разложить в ряд

Удерживая только первый член ряда, будем иметь т. е. для медленных нейтронов при a=1/ka >> RN рассеяние изотропно и определяется средней по объему величиной потенциала (его нулевой гармоникой). Это означает, что нейтрон "не чувствует пространственную структуру ядра. Ядро конечного радиуса рассеивает точно так же, как точечное, если интеграл одинаков Проиллюстрируем, почему структура потенциала не чувствуется медленной частицей, на примере потенциала вида Заметим, что любой потенциал можно представить как сумму дельтафункций, в силу определения самой -функции V(r) = V(r’) (r - r’) d 3 r’

Две рассеивающие точки на расстоянии R В этом случае, амплитуда рассеяния Сечение Когда ka. R << 1, то и q. R << 1, и сечение неотличимо от сечения рассеяния на потенциале (V 1+V 2) При q. R >>1, малое изменение q (как по величине, так и по направлению) приводит к множеству осцилляций cos поэтому в реальном эксперименте это слагаемое усредняется в нуль (r)

Парциальные волны Изотропность рассеяния при >> R связана с тем, чтов этом случае рассеяние происходит только с угловым моментом l=0 (в s-состоянии) Момент импульса налетающей частицы есть M = pb. С другой стороны, в квантовой механике он равен Ml = ħ [l(l+1]1/2, так что каждому значению орбитальногоквантового числа l соответствуетсвое прицельное расстояние (при заданном импульсе p):

Парциальные волны | Частицы с l 0 минуют область взаимодействия и не рассеиваются. Рассеивается только s-волна, остальные компоненты волновой функции остаются без изменения. Чтобы провзаимодействовать, нейтрон должен пройти на расстоянии RN от центра ядра, а поскольку это расстояние много меньше его длины волны, то мы не можем знать, с какой стороны от ядра проходит нейтрон. Нейтрон практически с одинаковой вероятностью проходит с обеих сторон ядра, а это означает, что его средний момент импульса равен нулю, то есть рассеяние происходит только в s-состоянии. Длины волн RN, при которых существенным становится рассеяние с l =1 (в p-состоянии), соответствуют энергиям нейтронов 10 Мэ. В. Если потенциал, в котором происходит рассеяние, обладает сферической симметрией, то момент количества движения является интегралом движения, т. е. состояния с разными моментами рассеиваются независимо. Поэтому падающую волну удобно представить в виде суперпозиции волн с разными моментами. Их и называют парциальными волнами.

Парциальные волны | Выбрав за полярную ось направление ka, напишем

Парциальные волны Наличие в плоской волне сходящейся и расходящейся волн отражает тот простой факт, что, с точки зрения классического радиального движения, свободная частица сначала приближается к центру, а потом удаляется от него. Что можно представить как отражение от потенциального барьера. Это и есть причина появления в уравнениях центробежного потенциала. Отступление
4th year lect2r.ppt