Лекция 2 Модели сетевого планирования и управления

Лекция № 2 Модели сетевого планирования и управления

ПЛАН ЛЕКЦИИ 1. 2. 3. 4. 5. 6. Введение. Сетевая модель и ее основные элементы. Метод критического пути. Правила построения сетевого графика. Примеры сетевых графиков. Расчет параметров сетевого графика.

ВВЕДЕНИЕ Метод сетевого планирования дает возможность определить, во-первых, какие работы или операции из числа многих, составляющих проект, являются «критическими» по своему влиянию на общую календарную продолжительность проекта и, во-вторых, каким образом построить наилучший календарный план проведения всех работ по данному проекту с тем, чтобы выдержать заданные сроки при минимальных затратах.

Дж. Е. Келли ПЕРВЫЙ ВАРИАНТ ЭТОГО МЕТОДА БЫЛ РАЗРАБОТАН В 1957 Г. АМЕРИКАНСКИМИ УЧЕНЫМИ ДЖ. Е. КЕЛЛИ И М. Р. УОКЕРОМ И БЫЛ НАЗВАНСРМ (ОТ НАЧАЛЬНЫХ БУКВ ВЫРАЖЕНИЯ « CRITICAL PATH METHOD» , ОЗНАЧАЮЩЕГО « МЕТОД КРИТИЧЕСКОГО ПУТИ» ). РИМЕРНО В ТО ЖЕ П ВРЕМЯ НЕЗАВИСИМО ОТ СРМ ПОЯВИЛАСЬ СИСТЕМА РЕRT ( «PROGRAM EVALUATION AND REVIEW TECHNIQUE» , ЧТО ОЗНАЧАЕТ « ТЕХНИКА ОБЗОРА И ОЦЕНКИ ПРОГРАММ» ).

СЕТЕВАЯ МОДЕЛЬ И ЕЕ ОСНОВНЫЕ ЭЛЕМЕНТЫ. Идея сетевого метода основана на графическом изображении комплекса работ с любой степенью их детализации и на выполнении элементарных арифметических операций по расчету параметров и анализу сетевых графиков.

С математической точки зрения сетевой график- это связный взвешенный орграф G= (A, R) без петель и контуров. При моделировании производственных процессов в качестве вершин графа используют события, а в качестве дугработы.

Событие- это момент начала или завершения одной или нескольких работ. Событие, которым начинается рассматриваемый комплекс работ, называется начальным. Событие, которым завершается комплекс работ, - конечным. Остальные события являются промежуточными.

Работа-любой трудовой процесс, сопровождающийся затратой времени и приводящий к нужным результатам. * На графе работы изображаются дугами Действительная работа - Фиктивная работа это реальный процесс, приводящий к достижению конкретных результатов и требующий затрат определенных ресурсов (материальных средств, времени, персонала). На сетевом графике работа изображается сплошной дугой. это условное изображение зависимости между действительными работами. На сетевом графике работа изображается пунктирной дугой. * Весом каждой дуги является продолжительность соответствующей работы

Любая последовательность работ, соединяющая какие-либо два события, называется путем. Путь, соединяющий исходное и конечное событие через последовательность работ, называется полным путем сетевого графика. Длительностью полного пути является сумма весов (продолжительностей по времени) входящих в него дуг (работ).

Полный путь максимальной продолжительности называется критическим. Критическими также называются работы и события, находящиеся на этом пути. Сумма продолжительностей всех критических работ называется критическим сроком выполнения комплекса работ. Чтобы достигнуть завершающего события, надо пройти обязательно весь критический путь. Для сокращения продолжительности выполнения комплекса работ необходимо в первую очередь сокращать продолжительность работ, лежащих на критическом пути.

3. ПРАВИЛА ПОСТРОЕНИЯ СЕТЕВОГО ГРАФИКА. Этапы. Подготовка исходных данных; сетевого планирования: Упорядочение сетевого графика; Составление сетевого графика; Определение критического пути и резервов времени; Анализ и оптимизация сетевого графика.

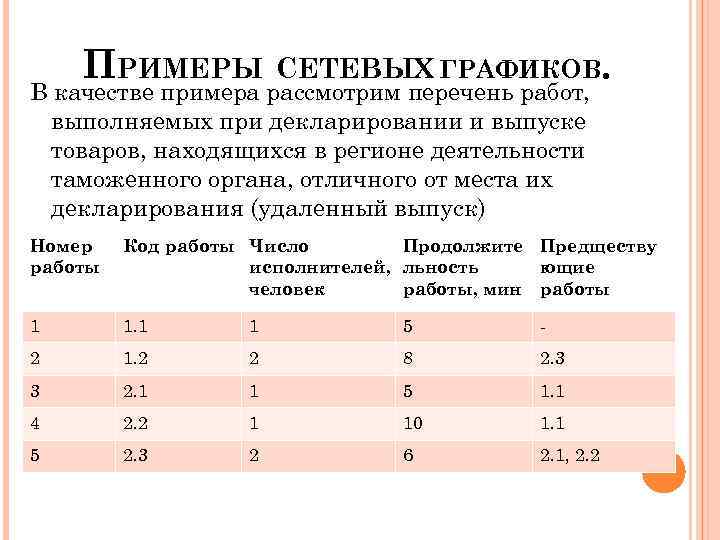ПРИМЕРЫ СЕТЕВЫХ ГРАФИКОВ. В качестве примера рассмотрим перечень работ, выполняемых при декларировании и выпуске товаров, находящихся в регионе деятельности таможенного органа, отличного от места их декларирования (удаленный выпуск) Таблица 1. Номер Код работы Число Продолжите Предществу работы исполнителей, льность ющие Перечень работ человек работы, мин работы 1 1 5 - 2 1. 2 2 8 2. 3 3 2. 1 1 5 1. 1 4 2. 2 1 10 1. 1 5 2. 3 2 6 2. 1, 2. 2

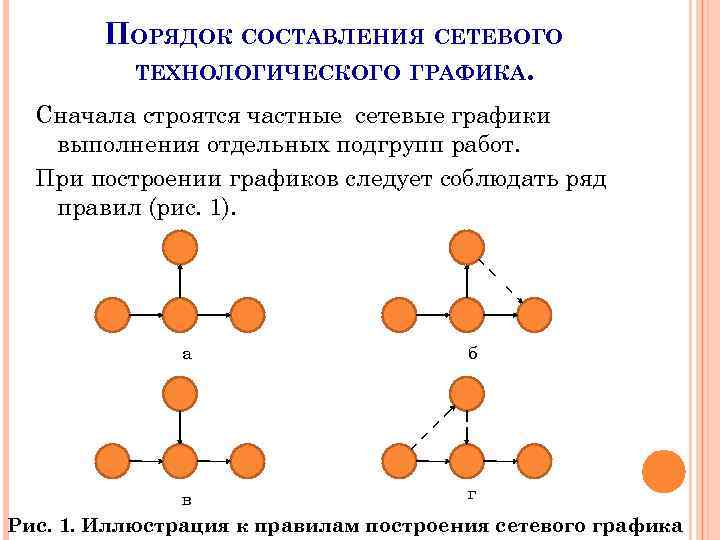ПОРЯДОК СОСТАВЛЕНИЯ СЕТЕВОГО ТЕХНОЛОГИЧЕСКОГО ГРАФИКА. Сначала строятся частные сетевые графики выполнения отдельных подгрупп работ. При построении графиков следует соблюдать ряд правил (рис. 1). а б в г Рис. 1. Иллюстрация к правилам построения сетевого графика

1. 2. 3. 4. 5. 6. В сетевом графике должны быть одно начальное и одно завершающее события. Если это не так, то вводятся фиктивные события и работы. Дуги, соединяющие события, могут иметь произвольную длину и произвольный наклон, но желательно избегать их пересечения. График не должен иметь туповиковых событий, т. е. событий, из которых не выходит ни одной дуги ( рис. 1, а). В этом случае вводят фиктивную работу ( рис. 1, б), показанную пунктирной дугой. График не должен содержать событий (за исключением начального события) в которые не входит ни одна дуга (рис. 1, в). В этом случае вводят фиктивную работу (рис. 1, г), показанную пунктирной дугой. Любые за два события- вершины графа- могут быть непосредственно связаны не более чем одной дугой. График не должен содержать замкнутых контуров и петель.

Построение частных сетевых графиков производится слева направо от исходного события к завершающему. При этом на графиках отмечаются лишь коды работ и их продолжительность. Затем проводят сшивание частных сетевых графиков в один путем совмещения крайних событий частных графиков и введения, если это нужно, фиктивных работ.

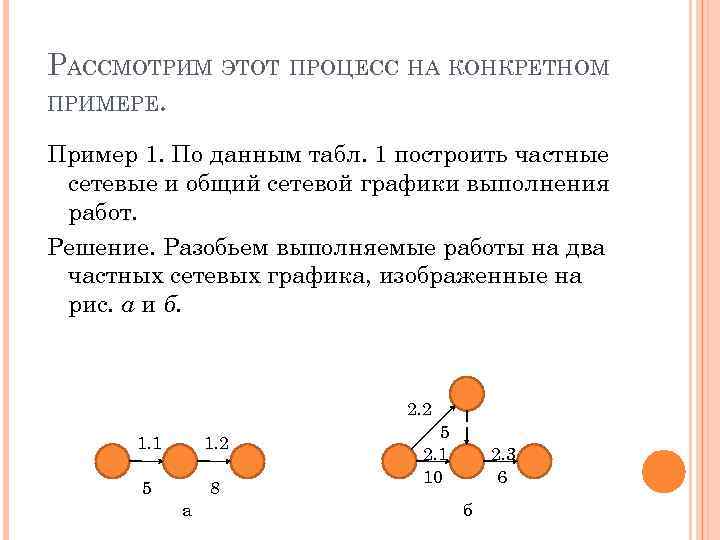РАССМОТРИМ ЭТОТ ПРОЦЕСС НА КОНКРЕТНОМ ПРИМЕРЕ. Пример 1. По данным табл. 1 построить частные сетевые и общий сетевой графики выполнения работ. Решение. Разобьем выполняемые работы на два частных сетевых графика, изображенные на рис. а и б. 2. 2 1. 1 1. 2 5 8 а 5 2. 1 10 2. 3 6 б

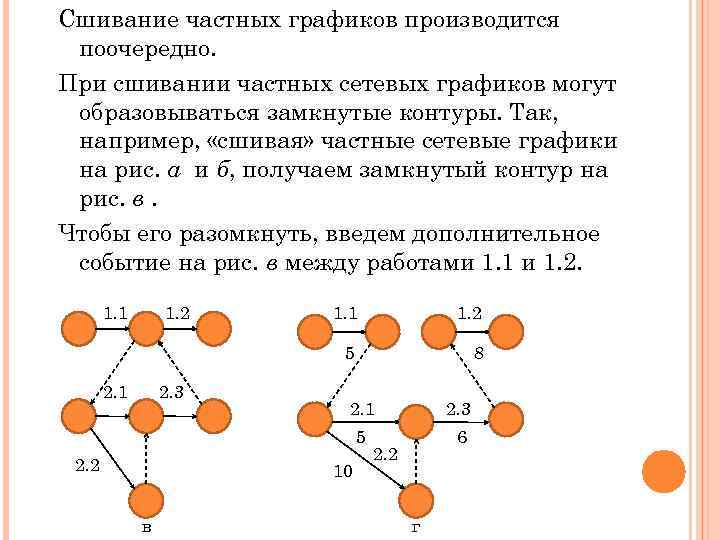Сшивание частных графиков производится поочередно. При сшивании частных сетевых графиков могут образовываться замкнутые контуры. Так, например, «сшивая» частные сетевые графики на рис. а и б, получаем замкнутый контур на рис. в. Чтобы его разомкнуть, введем дополнительное событие на рис. в между работами 1. 1 и 1. 2. 1. 1 1. 2 2. 3 1. 2 5 2. 1 1. 1 8 2. 3 5 2. 2 2. 1 6 10 в 2. 2 г

События, которые связаны только фиктивными работами, объединяются. После «сшивания» частных графиков в один производится нумерация событий общего графика (номер события указывается в кружке).

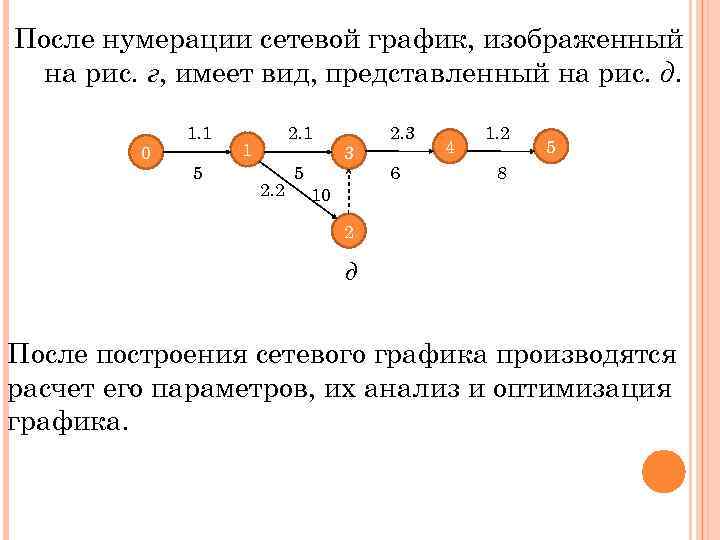После нумерации сетевой график, изображенный на рис. г, имеет вид, представленный на рис. д. 0 1. 1 5 2. 1 1 2. 2 5 3 2. 3 6 4 1. 2 5 8 10 2 д После построения сетевого графика производятся расчет его параметров, их анализ и оптимизация графика.

РАСЧЕТ ПАРАМЕТРОВ СЕТЕВОГО ГРАФИКА Основными параметрами сетевого технологического графика являются ранние и поздние сроки свершения событий, резервы времени наступления событий. Ранний срок свершения события t. P (j) – максимальная продолжительность времени выполнения всех работ от исходного события до рассматриваемого j-го события. Ранние сроки свершения событий определяются последовательно от начального события 0 к конечному N, в порядке нумерации событий, по формуле: t. P (j) = max { t. P (i) + t (i, j)} , t. P (0) = 0, i < j, t. P (N) = TКР, (5. 1) где t. P (i) – ранний срок свершения i-го события, предшествующего рассматриваемому j-му событию; t (i, j) – продолжительность работы, соединяющей i-е и j-е события.

Значения t. P могут быть определены непосредственно из графика с помощью мнемонического правила: устанавливаются события (по входящим стрелкам), которые непосредственно предшествуют рассматриваемому событию; к значениям t. P этих событий прибавляются длины дуг, соединяющих эти события с рассматриваемым, и из полученных сумм выбирается максимальная, которая и определяет собой значение t. P рассматриваемого события.

Поздний срок свершения события t. П (i) – максимальный допустимый срок наступления рассматриваемого i- го события, не приводящий к увеличению критического пути. Он показывает, через какое время после начала выполнения комплекса работ должно наступить интересующее событие, чтобы общая продолжительность работ не увеличивалась. Поздние сроки свершения событий определяются последовательно от завершающего события к исходному в порядке, обратном нумерации событий, по формуле: t. П (i) = min { t. П (j) - t. П (i, j) }, t. П (N) = t. P (N) = TКР, (5. 2) где t. П (j) – поздний срок свершения j-го события, которому непосредственно предшествует рассматриваемое i-е событие; t(i, j) – продолжительность работы (длина дуги), соединяющей i-е и j-е события.

Заметим, что значения t. П и t. P конечного события равны и соответствуют величине критического пути TКР. Это обстоятельство можно использовать для проверки правильности выполнения расчетов. Значения t. П также могут быть определены из графика с помощью мнемонического правила: • устанавливаются события (по выходящим дугам), которым непосредственно предшествует рассматриваемое событие; • из значений t. П этих событий вычитаются длины дуг, соединяющих эти события с рассматриваемым, и из полученных значений выбирается минимальная, которая и определяет собой значение t. П рассматриваемого события.

Резерв времени свершения события Δt(i) показывает, насколько можно сдвинуть срок наступления рассматриваемого события в сторону его увеличения, не увеличивая при этом критического пути: Δt(i) = t. П (i) - t. P (i). (5. 3)

После расчета параметров сетевого графика определяется критический путь. Для этого устанавливаются события с резервом времени свершения, равным нулю (Δt = 0). Критический путь будет пролегать между этими событиями, соединяя исходное и завершающее события непрерывной последовательности работ.

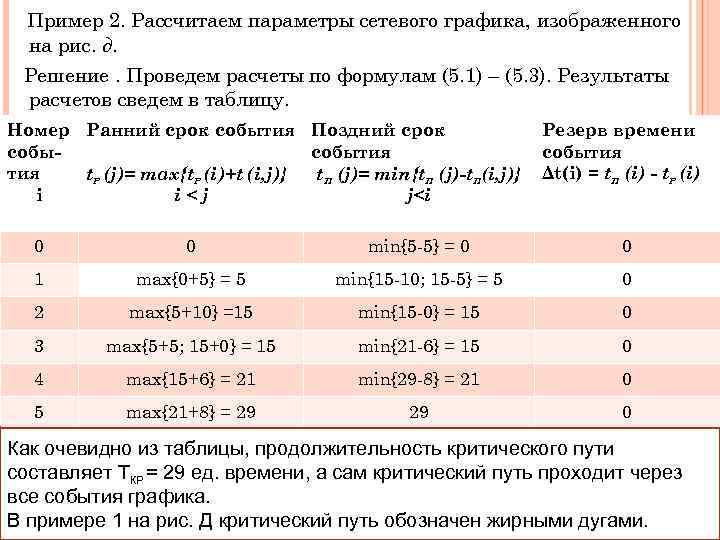Пример 2. Рассчитаем параметры сетевого графика, изображенного на рис. д. Решение. Проведем расчеты по формулам (5. 1) – (5. 3). Результаты расчетов сведем в таблицу. Номер Ранний срок события Поздний срок события t. P (j)= max{t. P (i)+t (i, j)} t. П (j)= min{t. П (j)-t. П(i, j)} i i

ЗАКЛЮЧЕНИЕ Сетевой метод планирования работ не дает строго оптимального решения. Однако путем последовательного многократного улучшения первоначального варианта можно получить график, близкий к оптимальному.

КРИТЕРИЯМИ ОПТИМАЛЬНОСТИ СЕТЕВОГО ГРАФИКА МОГУТ СЛУЖИТЬ: Коэффициенты загруженности αi или простоя βi i-го специалиста αi = Ti / TКР ; βi = 1 - αi ; Коэффициенты средней загруженности α или простоя β специалистов n α = ∑ Ti / n. TКР i=1 β = 1 - α, где Ti – суммарная продолжительность работы i-го специалиста; TКР - длина критического пути; n – число специалистов, задействованных в работах.

Признаками высокого качества технологического графика ( его близости к оптимальному) являются : близость значений αi , i= 1, n, к значению α, которые должны различаться не более чем на 0, 01; близость α к единице.