linalg02 векторы.ppt
- Количество слайдов: 81
 Лекция 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА. Определение 1. Операция T называется корректной относительно некоторого числового множества К, если
Лекция 2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА. Определение 1. Операция T называется корректной относительно некоторого числового множества К, если
 Определение 2. Числовым полем называется такое числовое множество К , в котом корректны операции сложения, вычитания, умножения и деления (кроме деления на ноль). Образуют поле множества рациональных чисел Q, действительных чисел R. Не образуют поле множества натуральных, целых, положительных, отрицательных.
Определение 2. Числовым полем называется такое числовое множество К , в котом корректны операции сложения, вычитания, умножения и деления (кроме деления на ноль). Образуют поле множества рациональных чисел Q, действительных чисел R. Не образуют поле множества натуральных, целых, положительных, отрицательных.
 Определение 3. Множество элементов любой математической природы называется линейным пространством над полем К, если выполнены следующие требования: А) Имеется правило- сумма элементов : B) Имеется правило- произведение элемента на число: С) Указанные два правила удовлетворяют следующим восьми аксиомам.
Определение 3. Множество элементов любой математической природы называется линейным пространством над полем К, если выполнены следующие требования: А) Имеется правило- сумма элементов : B) Имеется правило- произведение элемента на число: С) Указанные два правила удовлетворяют следующим восьми аксиомам.
 Аксиомы линейного пространства. I. Аксиомы операции сложения элементов: коммутативность сложения : ассоциативность сложения : особая роль нулевого элемента существование противоположного элемента
Аксиомы линейного пространства. I. Аксиомы операции сложения элементов: коммутативность сложения : ассоциативность сложения : особая роль нулевого элемента существование противоположного элемента
 II. Аксиомы операции умножения на число особая роль числового множителя 1. ассоциативность относительно числовых множителей.
II. Аксиомы операции умножения на число особая роль числового множителя 1. ассоциативность относительно числовых множителей.
 III. Аксиомы, связывающие операции сложения и умножения на число. дистрибутивность относительно суммы числовых множителей. дистрибутивность относительно суммы элементов.
III. Аксиомы, связывающие операции сложения и умножения на число. дистрибутивность относительно суммы числовых множителей. дистрибутивность относительно суммы элементов.
 При введении понятия линейного пространства абстрагируются не только от конкретной природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число. Важно лишь, чтобы эти правила удовлетворяли восьми аксиомам, входящим в определение 3. . Элементы произвольного линейного пространства принято называть векторами.
При введении понятия линейного пространства абстрагируются не только от конкретной природы изучаемых объектов, но и от конкретного вида правил образования суммы элементов и произведения элемента на число. Важно лишь, чтобы эти правила удовлетворяли восьми аксиомам, входящим в определение 3. . Элементы произвольного линейного пространства принято называть векторами.
 Примеры 1. Множества свободных векторов на прямой, на плоскости и в пространстве являются линейными пространствами. 2. Множества свободных векторов на плоскости и в трехмерном пространстве не параллельных некоторой прямой не являются линейными пространствами.
Примеры 1. Множества свободных векторов на прямой, на плоскости и в пространстве являются линейными пространствами. 2. Множества свободных векторов на плоскости и в трехмерном пространстве не параллельных некоторой прямой не являются линейными пространствами.
 3. Множество столбцов высоты n образует линейное пространство 4. Множество столбцов высоты n, сумма элементов которых равна 1 не образует линейного пространства.
3. Множество столбцов высоты n образует линейное пространство 4. Множество столбцов высоты n, сумма элементов которых равна 1 не образует линейного пространства.
 5. Множество матриц заданного размера mxn образует линейное пространство 6. Множество квадратных матриц заданного размера nxn с определителем = 0. не образует линейного пространства.
5. Множество матриц заданного размера mxn образует линейное пространство 6. Множество квадратных матриц заданного размера nxn с определителем = 0. не образует линейного пространства.
 7. Множество всех функций определенных и непрерывных на сегменте образует линейное пространство. 8. Множество всех функций не образует линейного пространства.
7. Множество всех функций определенных и непрерывных на сегменте образует линейное пространство. 8. Множество всех функций не образует линейного пространства.
 9. Множество всех алгебраических многочленов степени, не превышающей фиксированного натурального числа n образует линейное пространство. 10. Множество всех алгебраических многочленов степени, равной фиксированному натуральному числу n не образует линейного пространства. Линейное пространство может состоять либо из одного, либо из бесконечного числа элементов!
9. Множество всех алгебраических многочленов степени, не превышающей фиксированного натурального числа n образует линейное пространство. 10. Множество всех алгебраических многочленов степени, равной фиксированному натуральному числу n не образует линейного пространства. Линейное пространство может состоять либо из одного, либо из бесконечного числа элементов!
 Теоремы Теорема 1. В линейном пространстве R Доказательство.
Теоремы Теорема 1. В линейном пространстве R Доказательство.
 Теорема 2. В линейном пространстве R Доказательство.
Теорема 2. В линейном пространстве R Доказательство.
 Теорема 3. Доказательство.
Теорема 3. Доказательство.
 Теорема 4. Доказательство.
Теорема 4. Доказательство.
 Линейная зависимость системы векторов и ее геометрический смысл. Коллинеарные и компланарные векторы. Определение 4. Элемент называется линейной комбинацией элементов с коэффициентами
Линейная зависимость системы векторов и ее геометрический смысл. Коллинеарные и компланарные векторы. Определение 4. Элемент называется линейной комбинацией элементов с коэффициентами
 Вектор линейно выражается через векторы разлагается по векторам Определение 5. Элементы называются линейно зависимыми, если
Вектор линейно выражается через векторы разлагается по векторам Определение 5. Элементы называются линейно зависимыми, если
 Определение 6. Элементы называются линейно независимыми, если
Определение 6. Элементы называются линейно независимыми, если
 Cвойства линейной зависимости Теорема 5. Для того чтобы элементы были линейно зависимы необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных элементов.
Cвойства линейной зависимости Теорема 5. Для того чтобы элементы были линейно зависимы необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных элементов.
 Теорема 6. Если среди элементов имеется нулевой элемент, то эти элементы линейно зависимы. Доказательство. Система из одного вектора линейно зависима. Доказательство.
Теорема 6. Если среди элементов имеется нулевой элемент, то эти элементы линейно зависимы. Доказательство. Система из одного вектора линейно зависима. Доказательство.
 Теорема 7. Если часть элементов являются линейно зависимыми, то и все эти элементы являются линейно зависимыми.
Теорема 7. Если часть элементов являются линейно зависимыми, то и все эти элементы являются линейно зависимыми.
 Лестничная система векторов x 1, y 2, z 3, (числа, стоящие на "диагонали") отличны от нуля. Число векторов в лестничной системе не превосходит п (числа координат в каждом векторе). Любая лестничная система векторов линейно независима.
Лестничная система векторов x 1, y 2, z 3, (числа, стоящие на "диагонали") отличны от нуля. Число векторов в лестничной системе не превосходит п (числа координат в каждом векторе). Любая лестничная система векторов линейно независима.
 Коллинеарные вектора Компланарные вектора Теорема 8. В пространстве Rn, любая система из s векторов, где s>n, линейно зависима. Метод Гаусса можно использовать для исследования линейной зависимости. Имеет ли уравнение ненулевые решения? Система n линейных уравнений с s неизвестными. Если нулевое решение единственно- линейная независимость. Нет- линейная зависимость.
Коллинеарные вектора Компланарные вектора Теорема 8. В пространстве Rn, любая система из s векторов, где s>n, линейно зависима. Метод Гаусса можно использовать для исследования линейной зависимости. Имеет ли уравнение ненулевые решения? Система n линейных уравнений с s неизвестными. Если нулевое решение единственно- линейная независимость. Нет- линейная зависимость.
 Размерность и базис линейного пространства. Определение 7. Упорядоченная совокупность n линейно независимых элементов называется базисом линейного пространства если Разложение элемента Числа в базисе по базису -координаты элемента
Размерность и базис линейного пространства. Определение 7. Упорядоченная совокупность n линейно независимых элементов называется базисом линейного пространства если Разложение элемента Числа в базисе по базису -координаты элемента
 Определение 8. Натуральное число n называется размерностью линейного пространства если в R имеется n линейно независимых элементов, а любые n+1 элементов линейно зависимы. R называется n-мерным
Определение 8. Натуральное число n называется размерностью линейного пространства если в R имеется n линейно независимых элементов, а любые n+1 элементов линейно зависимы. R называется n-мерным
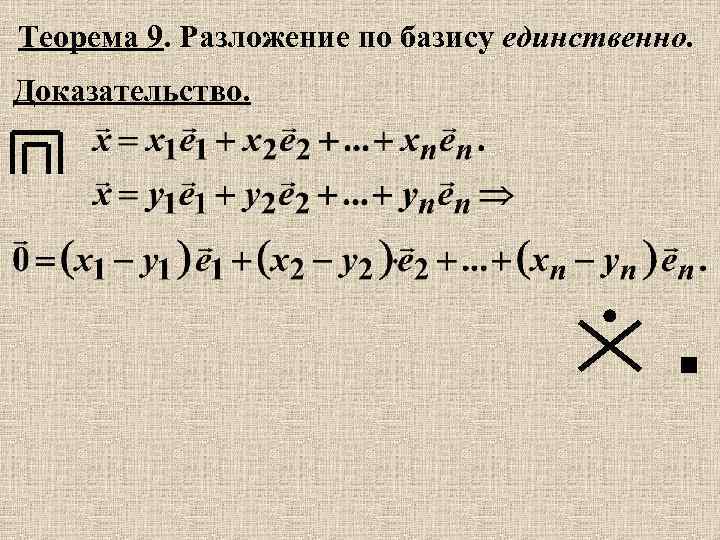 Теорема 9. Разложение по базису единственно. Доказательство.
Теорема 9. Разложение по базису единственно. Доказательство.
 Теорема 10. При сложении любых двух элементов линейного пространства их координаты (относительно любого фиксированного базиса) складываются; при умножении произвольного элемента на любое число все координаты этого элемента умножаются на это число. Теорема 11. Если линейное пространство имеет размерность n, то любые n линейно независимых элементов этого пространства образуют его базис.
Теорема 10. При сложении любых двух элементов линейного пространства их координаты (относительно любого фиксированного базиса) складываются; при умножении произвольного элемента на любое число все координаты этого элемента умножаются на это число. Теорема 11. Если линейное пространство имеет размерность n, то любые n линейно независимых элементов этого пространства образуют его базис.
 Теорема 12. Если линейное пространство имеет базис, состоящий из n элементов, то его размерность равна n. Канонический базис.
Теорема 12. Если линейное пространство имеет базис, состоящий из n элементов, то его размерность равна n. Канонический базис.
 Пусть в линейном пространстве даны два произвольных базиса Разложим элементы базиса F по базису E:
Пусть в линейном пространстве даны два произвольных базиса Разложим элементы базиса F по базису E:
 Матрица A - матрица перехода от E к F. В j-ом столбце матрицы перехода стоят координаты вектора столбец координат в базисе E. столбец координат в базисе F
Матрица A - матрица перехода от E к F. В j-ом столбце матрицы перехода стоят координаты вектора столбец координат в базисе E. столбец координат в базисе F
 Формулы преобразования координат вектора при преобразовании базиса (при переходе к новому базису).
Формулы преобразования координат вектора при преобразовании базиса (при переходе к новому базису).
 ПОДПРОСТРАНСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ И ЛИНЕЙНЫЕ ОБОЛОЧКИ Определение 1. Подпространством линейного пространства R над полем К называется любое непустое подмножество M этого пространства, на котором корректны операции сложения элементов и умножения элемента на число, которые введены в исходном линейном пространстве R:
ПОДПРОСТРАНСТВА ЛИНЕЙНЫХ ПРОСТРАНСТВ И ЛИНЕЙНЫЕ ОБОЛОЧКИ Определение 1. Подпространством линейного пространства R над полем К называется любое непустое подмножество M этого пространства, на котором корректны операции сложения элементов и умножения элемента на число, которые введены в исходном линейном пространстве R:
 Свойства подпространств. 1) Всякое подпространство линейного пространства само является линейным пространством. 2) Размерность подпространства не превосходит размерности самого линейного пространства. 3) Если базис в подпространстве M линейного пространства R размерности n и k
Свойства подпространств. 1) Всякое подпространство линейного пространства само является линейным пространством. 2) Размерность подпространства не превосходит размерности самого линейного пространства. 3) Если базис в подпространстве M линейного пространства R размерности n и k
 Линейные оболочки Определение 2. Линейной оболочкой элементов линейного пространства называется множество всех линейных комбинаций этих элементов. -порождающая система.
Линейные оболочки Определение 2. Линейной оболочкой элементов линейного пространства называется множество всех линейных комбинаций этих элементов. -порождающая система.
 Свойства линейных оболочек. -подпространство R. наименьшее подпространство, содержащее элементы 3) Если какой-либо элемент из есть линейная комбинация остальных элементов то его можно удалить из порождающей системы, не изменив при этом линейной оболочки.
Свойства линейных оболочек. -подпространство R. наименьшее подпространство, содержащее элементы 3) Если какой-либо элемент из есть линейная комбинация остальных элементов то его можно удалить из порождающей системы, не изменив при этом линейной оболочки.
 4) Пусть среди порождающей системы элементов имеется р линейно независимых элементов, например, а остальные элементы представляют собой линейные комбинации первых р элементов. Тогда: базис в
4) Пусть среди порождающей системы элементов имеется р линейно независимых элементов, например, а остальные элементы представляют собой линейные комбинации первых р элементов. Тогда: базис в
 ЕВКЛИДОВЫ ПРОСТРАНСТВА Определение 1. Линейное пространство R называется евклидовым, если в нем указано правило, -число, называемое скалярным произведением.
ЕВКЛИДОВЫ ПРОСТРАНСТВА Определение 1. Линейное пространство R называется евклидовым, если в нем указано правило, -число, называемое скалярным произведением.
 это правило удовлетворяет четырем аксиомам:
это правило удовлетворяет четырем аксиомам:
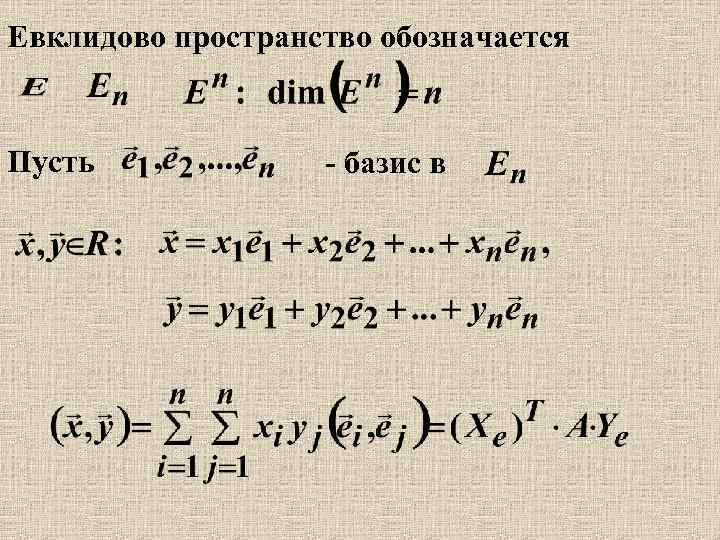 Евклидово пространство обозначается Пусть - базис в
Евклидово пространство обозначается Пусть - базис в
 столбцы координат векторов в базисе
столбцы координат векторов в базисе
 Определение 2. Длиной (нормой) элемента называется число Элемент, длина которого равна единице, называется нормированным.
Определение 2. Длиной (нормой) элемента называется число Элемент, длина которого равна единице, называется нормированным.
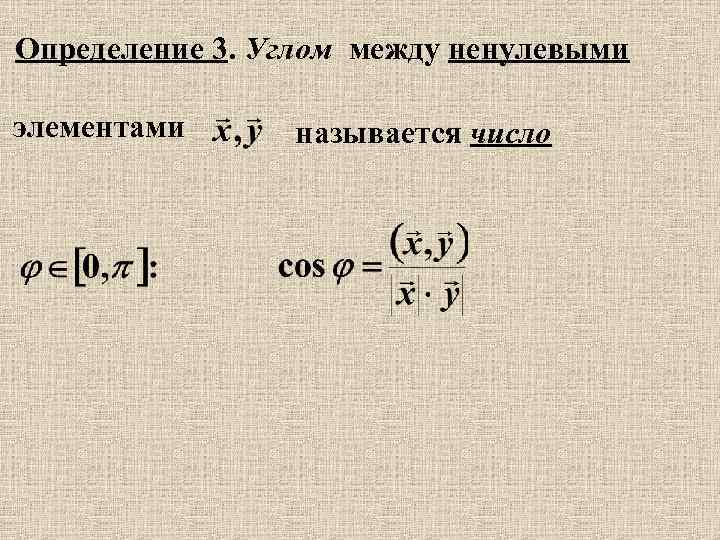 Определение 3. Углом между ненулевыми элементами называется число
Определение 3. Углом между ненулевыми элементами называется число
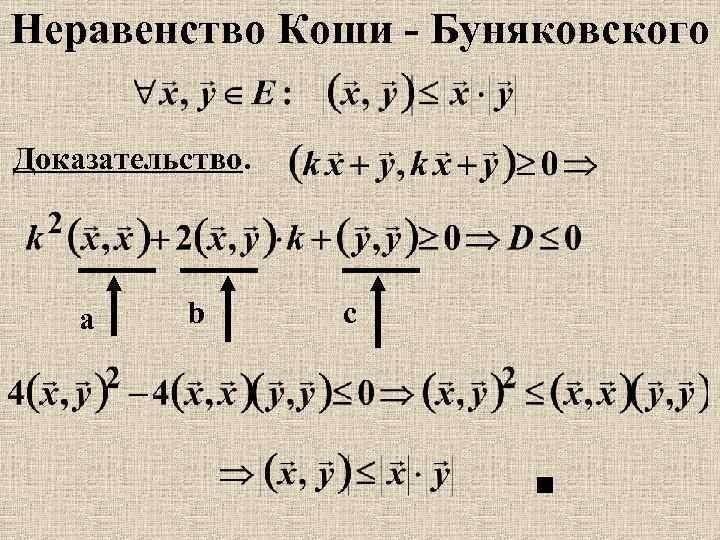 Неравенство Коши - Буняковского Доказательство. a b c
Неравенство Коши - Буняковского Доказательство. a b c
 Определение 4. Элементы называются ортогональными, если Определение 5. Система элементов называется ортогональной, если
Определение 4. Элементы называются ортогональными, если Определение 5. Система элементов называется ортогональной, если
 Определение 6. Система элементов называется ортонормированной, если где - символ Кронекера.
Определение 6. Система элементов называется ортонормированной, если где - символ Кронекера.
 Теорема 1. Любая ортогональная система ненулевых элементов является линейно независимой. Доказательство. Пусть ортогональная система, т. е. Пусть они линейно зависимы, т. е
Теорема 1. Любая ортогональная система ненулевых элементов является линейно независимой. Доказательство. Пусть ортогональная система, т. е. Пусть они линейно зависимы, т. е
 Умножим обе части (*) скалярно на и учтем условие ортогональности:
Умножим обе части (*) скалярно на и учтем условие ортогональности:
 Теорема 2. В евклидовом пространстве существует ортонормированный базис (ОНБ). Доказательство. Поскольку то линейно независимые – базис.
Теорема 2. В евклидовом пространстве существует ортонормированный базис (ОНБ). Доказательство. Поскольку то линейно независимые – базис.
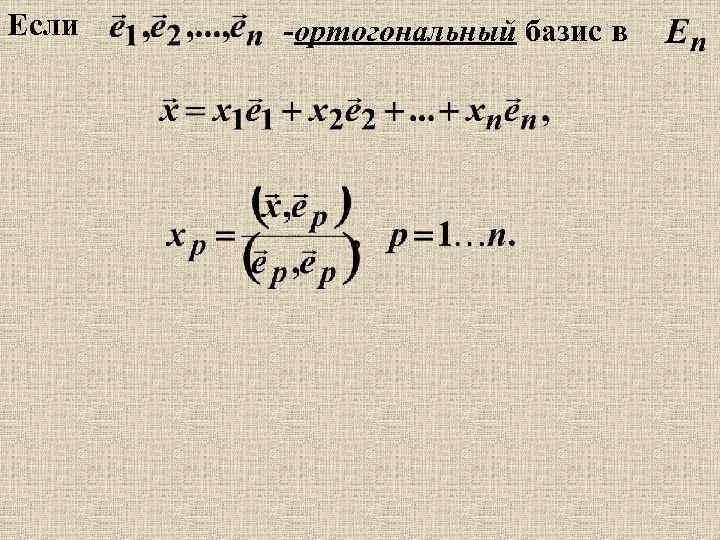 Если -ортогональный базис в
Если -ортогональный базис в
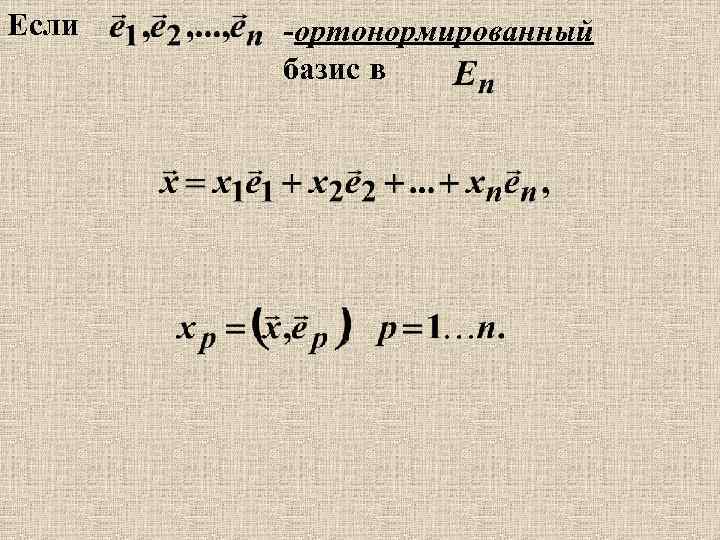 Если -ортонормированный базис в
Если -ортонормированный базис в
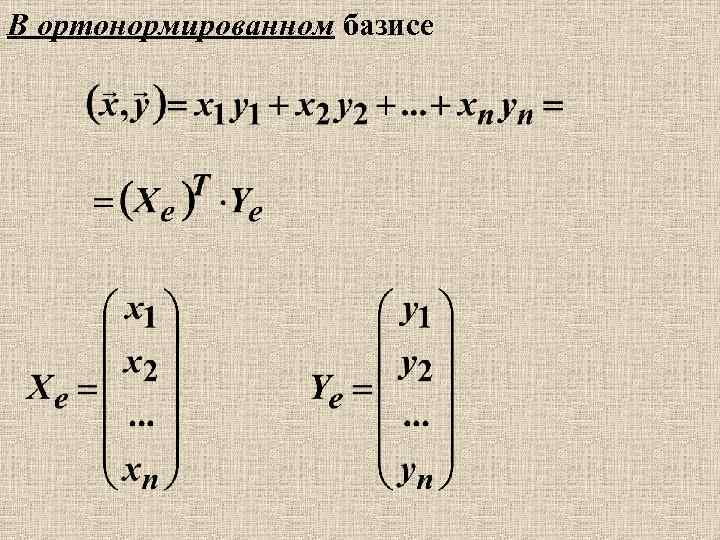 В ортонормированном базисе
В ортонормированном базисе
 Справедливо и обратное утверждение: если в некотором базисе для любых элементов данного пространства скалярное произведение вычисляется по предыдущей формуле, то указанный базис является ортонормированным.
Справедливо и обратное утверждение: если в некотором базисе для любых элементов данного пространства скалярное произведение вычисляется по предыдущей формуле, то указанный базис является ортонормированным.
 ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ Определение 1. Линейным оператором действующим в линейном пространстве (линейным преобразованием линейного пространства), называется правило
ЛИНЕЙНЫЕ ОПЕРАТОРЫ В КОНЕЧНОМЕРНЫХ ПРОСТРАНСТВАХ Определение 1. Линейным оператором действующим в линейном пространстве (линейным преобразованием линейного пространства), называется правило
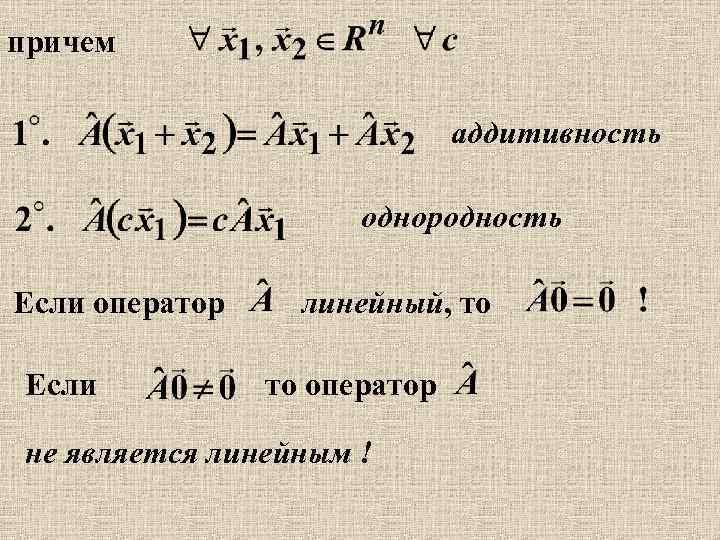 причем аддитивность однородность Если оператор Если линейный, то то оператор не является линейным !
причем аддитивность однородность Если оператор Если линейный, то то оператор не является линейным !
 образ прообраз Определение 2. Оператор называется нулевым оператором. Определение 3. Оператор называется тождественным или единичным оператором.
образ прообраз Определение 2. Оператор называется нулевым оператором. Определение 3. Оператор называется тождественным или единичным оператором.
 Примеры операторов 1) Оператор проектирования вектора на прямую (плоскость) 2) Оператор симметричного отражения вектора относительно прямой (плоскости) 3) Оператор поворота вектора 4) Оператор транспонирования матрицы (для пространства квадратных матриц) 5) Оператор дифференцирования - Линейные операторы
Примеры операторов 1) Оператор проектирования вектора на прямую (плоскость) 2) Оператор симметричного отражения вектора относительно прямой (плоскости) 3) Оператор поворота вектора 4) Оператор транспонирования матрицы (для пространства квадратных матриц) 5) Оператор дифференцирования - Линейные операторы
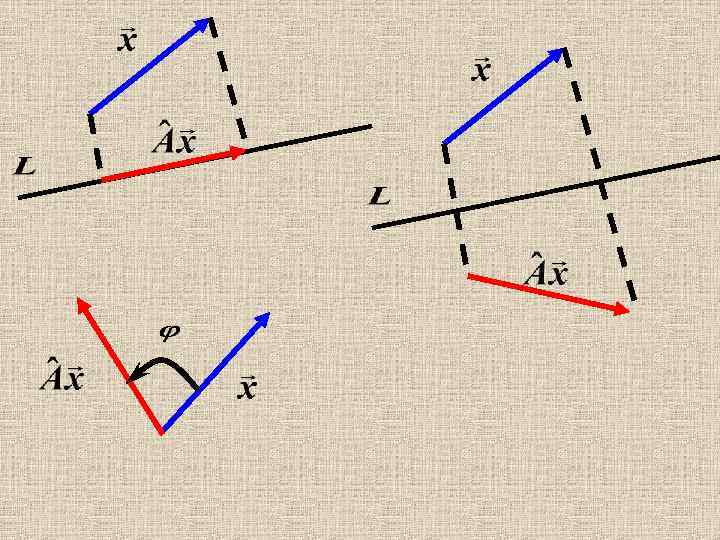
 6) Оператор параллельного переноса (сдвига) Не является линейным !
6) Оператор параллельного переноса (сдвига) Не является линейным !
 Определение 4. Суммой линейных операторов и называют оператор Определение 5. Произведением линейного оператора называют оператор на число
Определение 4. Суммой линейных операторов и называют оператор Определение 5. Произведением линейного оператора называют оператор на число
 Определение 6. Произведением линейных операторов и называют оператор Определение 7. Операторы называются равными, если и
Определение 6. Произведением линейных операторов и называют оператор Определение 7. Операторы называются равными, если и
 Теорема 1. Если и линейные операторы то - линейные операторы.
Теорема 1. Если и линейные операторы то - линейные операторы.
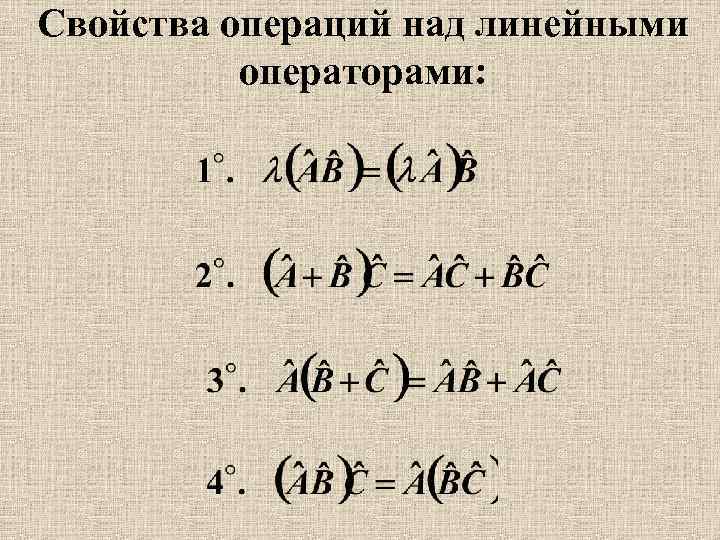 Свойства операций над линейными операторами:
Свойства операций над линейными операторами:
 Матричная запись линейных операторов Разложим элементы по базису
Матричная запись линейных операторов Разложим элементы по базису
 матрица оператора в базисе
матрица оператора в базисе
 Определение 8. Линейный оператор называется обратным к оператору если
Определение 8. Линейный оператор называется обратным к оператору если
 Теорема 2. Если операторы равны, то в любом базисе равны и матрицы этих операторов. Теорема 3.
Теорема 2. Если операторы равны, то в любом базисе равны и матрицы этих операторов. Теорема 3.
 Теорема 4. При переходе от базиса к базису Доказательство
Теорема 4. При переходе от базиса к базису Доказательство
 Пример 1. Пусть оператор действует по правилу В базисе Найдем матрицы операторов и явный вид обратного оператора
Пример 1. Пусть оператор действует по правилу В базисе Найдем матрицы операторов и явный вид обратного оператора
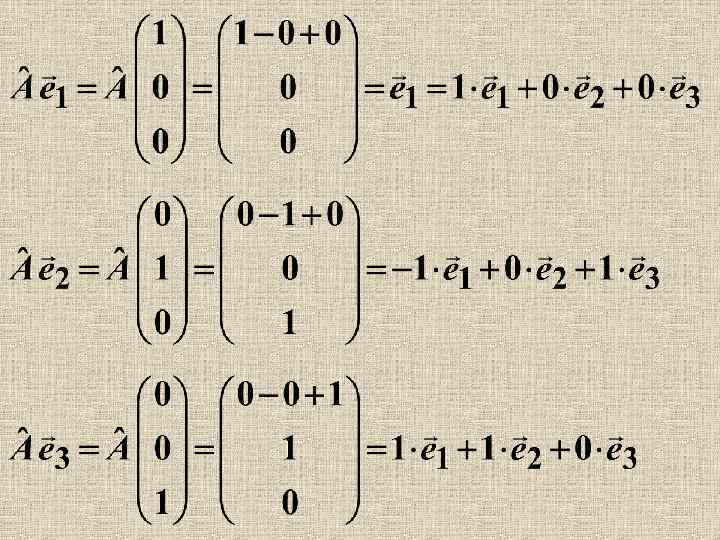
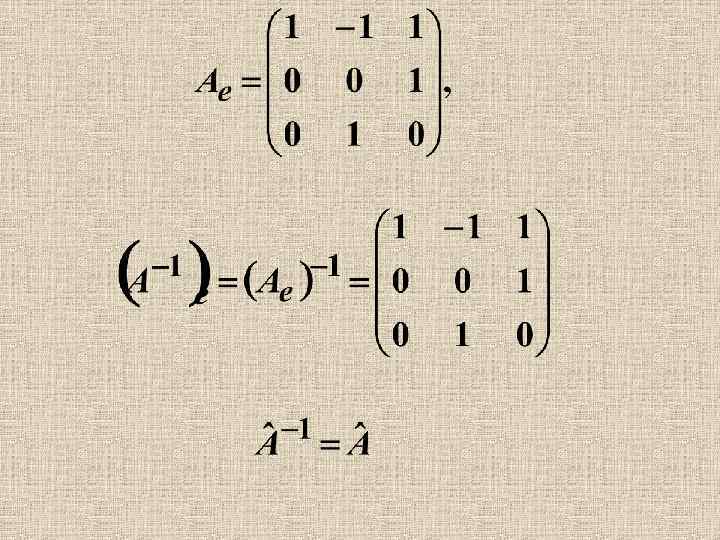
 СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНОГО ОПЕРАТОРА Определение 1. Подпространство M линейного пространства Rn называется инвариантным относительно линейного оператора A, если Пространство Rn и нуль-пространство 0 всегда являются инвариантными подпространствами для линейного A Rn Rn.
СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНОГО ОПЕРАТОРА Определение 1. Подпространство M линейного пространства Rn называется инвариантным относительно линейного оператора A, если Пространство Rn и нуль-пространство 0 всегда являются инвариантными подпространствами для линейного A Rn Rn.
 Определение 2. Число l называется собственным значением (собственным числом) линейного оператора A , если называется собственным вектором линейного оператора A, отвечающим собственному числу l.
Определение 2. Число l называется собственным значением (собственным числом) линейного оператора A , если называется собственным вектором линейного оператора A, отвечающим собственному числу l.
 Определение 3. Уравнение называется характеристическим уравнением линейного оператора A Rn , имеющего в базисe матрицу Многочлен называется характеристическим многочленом оператора A в базисе E.
Определение 3. Уравнение называется характеристическим уравнением линейного оператора A Rn , имеющего в базисe матрицу Многочлен называется характеристическим многочленом оператора A в базисе E.
 Теорема 1. Характеристический многочлен оператора A не зависит от выбора базиса. Теорема 2. Для того чтобы число l было собственным значением оператора A необходимо и достаточно, чтобы это число было корнем характеристического уравнения оператора A. Теорема 3. Пусть собственные числа оператора A различны. Тогда отвечающие им собственные векторы линейно независимы.
Теорема 1. Характеристический многочлен оператора A не зависит от выбора базиса. Теорема 2. Для того чтобы число l было собственным значением оператора A необходимо и достаточно, чтобы это число было корнем характеристического уравнения оператора A. Теорема 3. Пусть собственные числа оператора A различны. Тогда отвечающие им собственные векторы линейно независимы.
 Определение 4. Базис в Rn, в котором действует линейный оператор A, составленный из собственных векторов оператора A (если такой базис существует), называется собственным базисом оператора A. Теорема 4. Для того чтобы матрица линейного оператора A в данном базисе была диагональной, необходимо и достаточно, чтобы этот базис был собственным базисом оператора A.
Определение 4. Базис в Rn, в котором действует линейный оператор A, составленный из собственных векторов оператора A (если такой базис существует), называется собственным базисом оператора A. Теорема 4. Для того чтобы матрица линейного оператора A в данном базисе была диагональной, необходимо и достаточно, чтобы этот базис был собственным базисом оператора A.
 Свойства собственных векторов и собственных значений самосопряженных (симметрических) операторов. 1) Все n корней характеристического уравнения симметричного оператора - действительные числа. 2) Симметричный оператор всегда имеет собственные векторы. 3) Собственные векторы симметричного оператора, отвечающие различным собственным числам, ортогональны.
Свойства собственных векторов и собственных значений самосопряженных (симметрических) операторов. 1) Все n корней характеристического уравнения симметричного оператора - действительные числа. 2) Симметричный оператор всегда имеет собственные векторы. 3) Собственные векторы симметричного оператора, отвечающие различным собственным числам, ортогональны.
 4) Для симметричного оператора существует ортонормированный собственный базис. Пример. Найти собственные значения и собственные вектоpы линейного оператора, заданного матpицей Решение. Для нахождения собственных значений запишем характеристическое уравнение:
4) Для симметричного оператора существует ортонормированный собственный базис. Пример. Найти собственные значения и собственные вектоpы линейного оператора, заданного матpицей Решение. Для нахождения собственных значений запишем характеристическое уравнение:
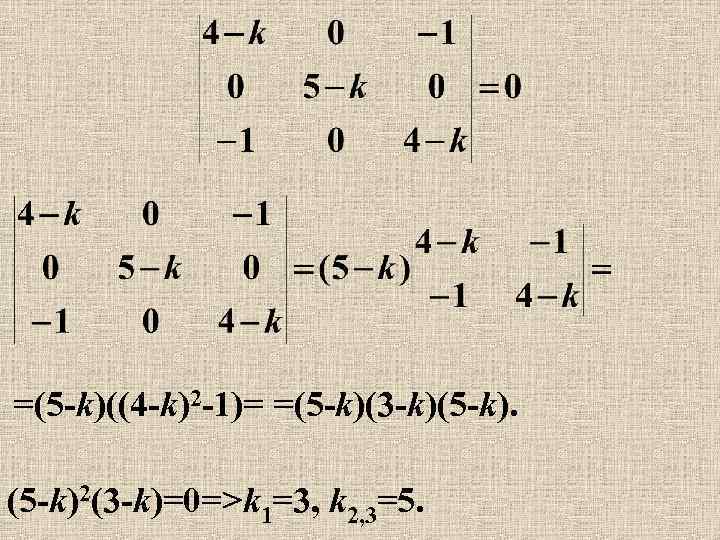 =(5 -k)((4 -k)2 -1)= =(5 -k)(3 -k)(5 -k)2(3 -k)=0=>k 1=3, k 2, 3=5.
=(5 -k)((4 -k)2 -1)= =(5 -k)(3 -k)(5 -k)2(3 -k)=0=>k 1=3, k 2, 3=5.
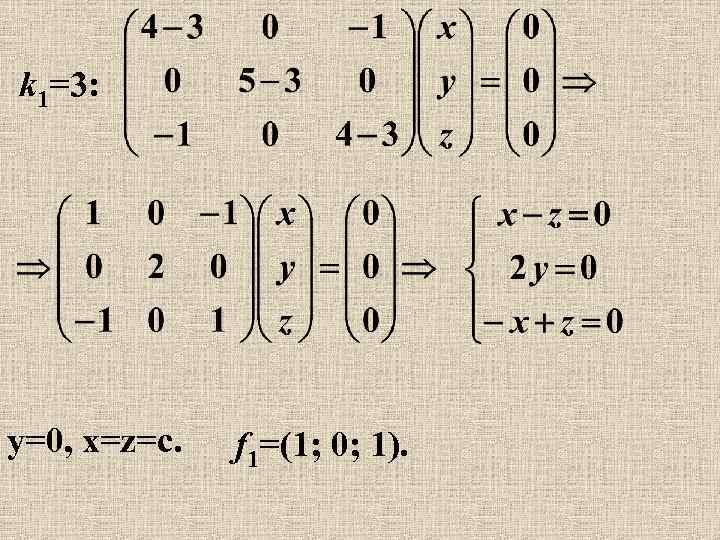 k 1=3: y=0, x=z=c. f 1=(1; 0; 1).
k 1=3: y=0, x=z=c. f 1=(1; 0; 1).
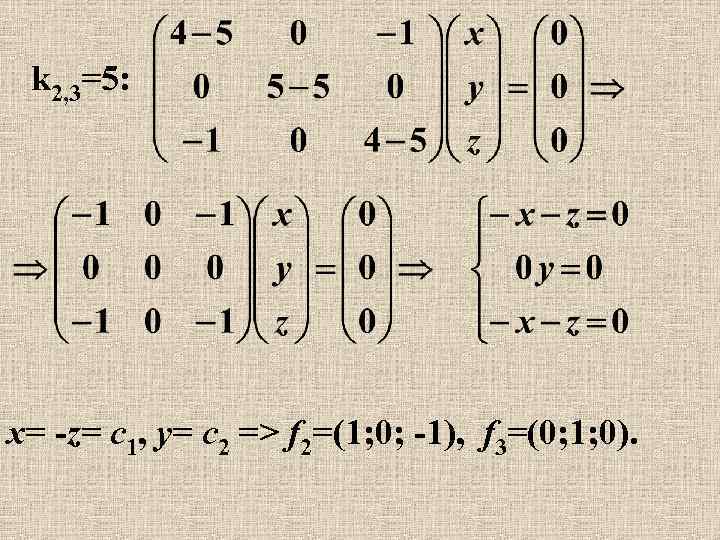 k 2, 3=5: x= -z= c 1, y= c 2 => f 2=(1; 0; -1), f 3=(0; 1; 0).
k 2, 3=5: x= -z= c 1, y= c 2 => f 2=(1; 0; -1), f 3=(0; 1; 0).


