Лекция 2 Квантиль распределения Оценка математического ожидания Оценка

Лекция 2 Квантиль распределения Оценка математического ожидания Оценка дисперсии и стандартного отклонения Мода Медиана Эксцесс Асимметрия Описательная статистика (программа «Анализ данных» ) Нормальное распределение и его свойства 1

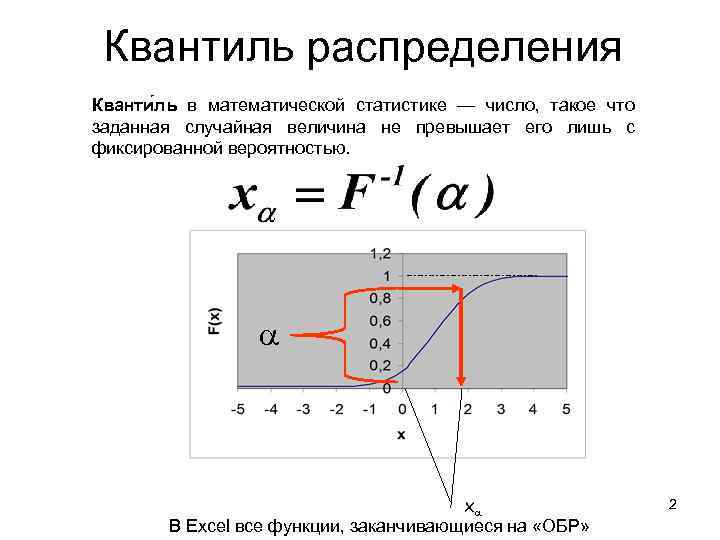Квантиль распределения Кванти ль в математической статистике — число, такое что заданная случайная величина не превышает его лишь с фиксированной вероятностью. x В Excel все функции, заканчивающиеся на «ОБР» 2

ПЕРСЕНТИЛЬ (PERCENTILE) Возвращает k-ую персентиль для значений из интервала. Эта функция используется для определения порога приемлемости. Например, можно принять решение экзаменовать только тех кандидатов, которые набрали баллов более, чем 90 -ая персентиль k — значение персентили в интервале от 0 до 1 включительно 3

Понятие ОЦЕНКИ ПАРАМЕТРА Выборочная (статистическая характеристика), используемая в качестве приближенного значения неизвестного истинного (генерального) параметра распределения случайной величины называется точечной оценкой. 4

Понятие ОЦЕНКИ ПАРАМЕТРА Статистическая характеристика является случайной величиной, т. к. ее значение зависит от конкретной выборки. Пусть q – параметр, q*- оценка параметра. 5

Свойства оценок • Состоятельность • Эффективность • Несмещенность 6

Требования к оценке параметра (при условии увеличения числа опытов) 1)состоятельность оценки (сходимость по вероятности): P( q-q* ) < = 1 - 7

Требования к оценке параметра (при условии увеличения числа опытов) 2)несмещенность: M(q*)=q. Математическое ожидание оценки параметра должно равняться самому параметру. 8

Требования к оценке параметра (при условии увеличения числа опытов) 3)эффективность: Дисперсия оценки должна быть минимальной из всех среди других возможных оценок. 9

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ - сумма произведений всех возможных значений СВ на вероятности этих значений. 10

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ а) для дискретной случайной величины X MX= , где n-количество возможных значений случайной величины, xi-конкретные реализации случайной величины, pi- вероятности, с которыми они могут произойти;

МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ СЛУЧАЙНОЙ ВЕЛИЧИНЫ б) для непрерывной случайной величины:

ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ - это математическое ожидание квадрата отклонения случайной величины от ее среднего значения

ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 1) для дискретной случайной величины –

ДИСПЕРСИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ 2)для непрерывной случайной величины – D = (x- MX)2 p(x) dx -

Оценка МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ – СТАТИСТИЧЕСКОЕ СРЕДНЕЕ ВЫБОРКИ (функции СРЗНАЧ, MEAN) mi- число реализаций xi опыте. в i-том

Оценка МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ – СТАТИСТИЧЕСКОЕ СРЕДНЕЕ ВЫБОРКИ Оценка математического ожидания – среднее значение является случайной величиной.

Оценка ДИСПЕРСИИ (2 вида оценки) 1)Статистическая дисперсия (дисперсия генеральной совокупности – в терминах EXCEL – ДИСПР ) D*= ( [xi- ]2)/n , где n –длина выборки, - статистическое среднее

Оценка ДИСПЕРСИИ (2 вида оценки) 2)Несмещенная оценка (дисперсия выборки– в терминах EXCEL – ДИСП ) = ( [xi- ]2)/(n-1)

СРЕДНЕЕ КВАДРАТИЧЕСКОЕ или СТАНДАРТНОЕ ОТКЛОНЕНИЕ (в EXCEL - СТДОТКЛОН, STDEV) Оценка стандартного отклонения по выборке

КОЭФФИЦИЕНТ ВАРИАЦИИ (изменчивости) Служит безразмерной оценкой разброса выборки.

СТАТИСТИЧЕСКИЙ КОЭФФИЦИЕНТ ВАРИАЦИИ (оценка по выборке) На практике желательно, чтобы <=33%.

МОДА (MODE)

МОДА x

МЕДИАНА (MEDIAN)

Стандартная ошибка (не путать со стандартным отклонением)

Пример

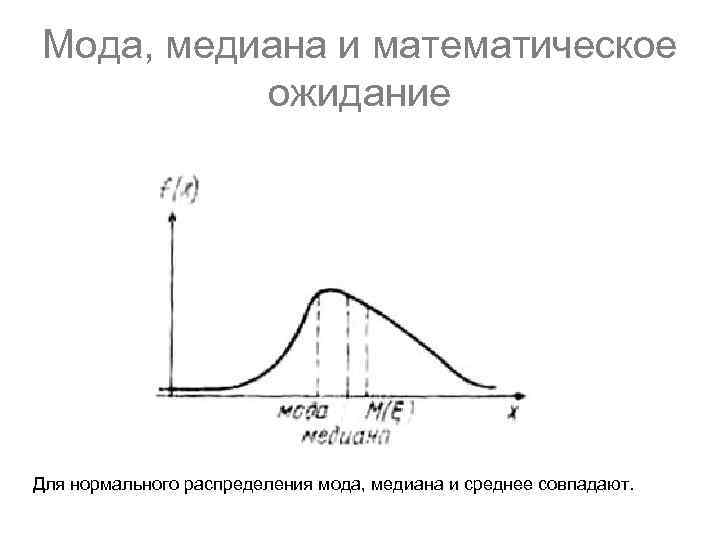Мода, медиана и математическое ожидание Для нормального распределения мода, медиана и среднее совпадают.

Эксцесс (KURT)

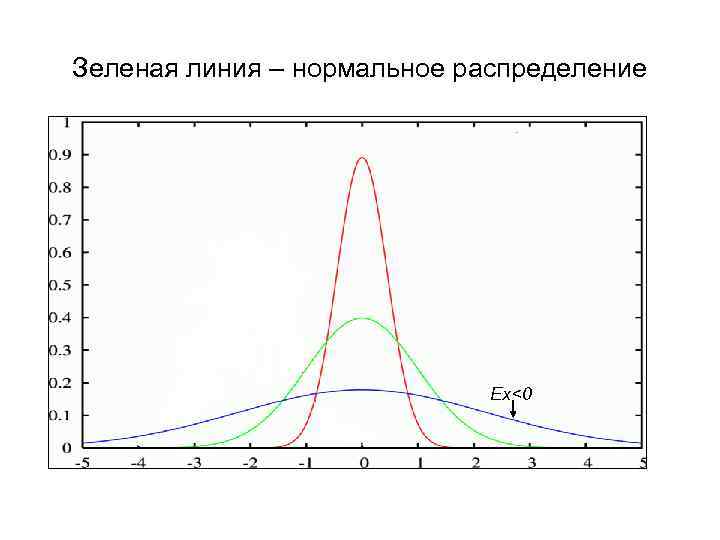Зеленая линия – нормальное распределение Ex<0

Коэффициент асимметрии (СКОС, SKEW)

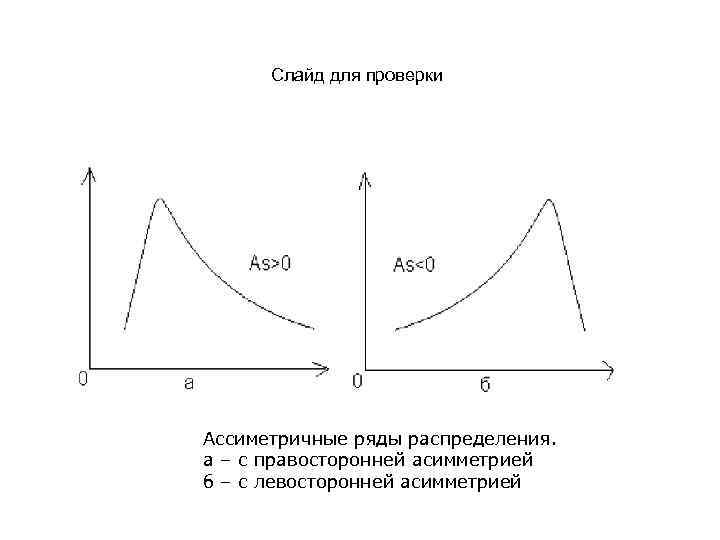Слайд для проверки Ассиметричные ряды распределения. а – с правосторонней асимметрией б – с левосторонней асимметрией

ПРОГРАММА «Описательная статистика» • Анализ данных->Описательная статистика

Расчет описательных статистик в MS Excel 2007: • • • 1. Установка надстройки «Пакет анализа» : Щелкните значок «Кнопка Microsoft Office» , затем щелкните параметры Excel. Перейдите на вкладку «Надстройки» , затем в поле «Управление» выберите «Надстройки Excel» Нажмите кнопку «Перейти» В поле Доступные надстройки установите флажок Пакет анализа и нажмите Ok 2. Расчет описательных статистик: На вкладке «Данные» в группе «Анализ» выберите «Анализ данных» В появившемся списке выберите «Описательная статистика» Задайте диапазон данных и отметьте пункт «Итоговая стастистика»

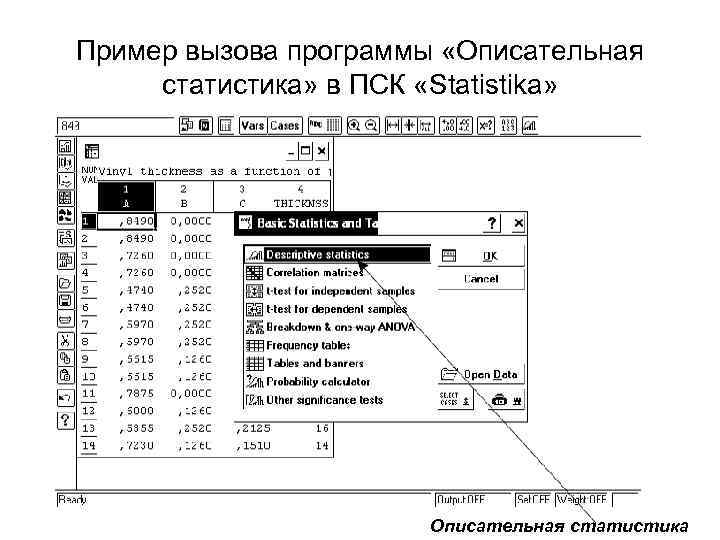Пример вызова программы «Описательная статистика» в ПСК «Statistika» Описательная статистика

ПРОГРАММА «Описательная статистика»

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (или РАСПРЕДЕЛЕНИЕ ГАУССА) 37

Параметры • • μ – коэффициент сдвига σ2 > 0 – коэффициент масштаба Математическое ожидание μ Медиана μ Мода μ Дисперсия σ2 Коэффициент асимметрии 0 Коэффициент эксцесса 0 38

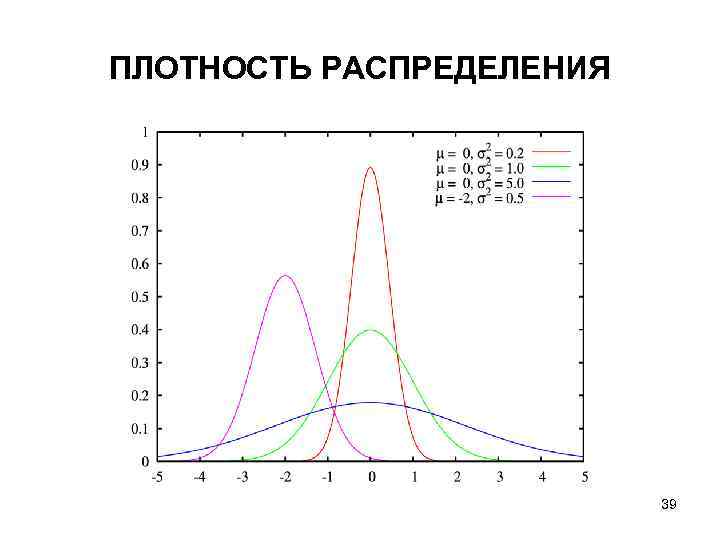ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ 39

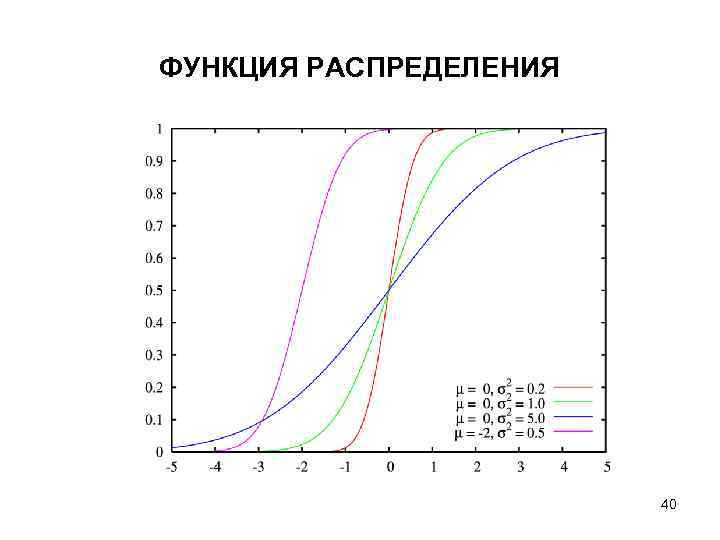ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ 40

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ (или РАСПРЕДЕЛЕНИЕ ГАУССА) N(μ, σ2) 41

Стандартное нормальное распределение • называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1. Обозначение N(0, 1) МОЖНО ПОЛУЧИТЬ нормальное РАСПРЕДЕЛЕНИЕ С ЛЮБЫМИ ПАРАМЕТРАМИ 42

Свойства нормального распределения • с вероятностью 68. 2% такая случайная величина принимает значения в интервале (μ - , μ + ) • c вероятностью 95. 46% такая случайная величина принимает значения в интервале (μ -2 , μ+2 ); • c вероятностью 99. 7% такая случайная величина принимает значения в интервале (μ -3 , μ +3 ). 43

Функции в Excel (Open. Office), связанные с нормальным распределением • • НОРМРАСП (NORMDIST) НОРМОБР (NORMINV) НОРМСТРАСП (NORMSDIST) НОРМСТОБР (NORMSINV) 44

Для нормального распределения мода, медиана и среднее совпадают. 45

Литература Н. В. Макарова В. Я. Трофимец Статистика в Excel М. Финансы и статистика 2002. Гусейнзаде М. А. , Калинина Э. В. , Добкина М. Б. Методы математической статистики в нефтяной и газовой промышленности 46