ЛЕКЦИЯ 2 Комплексные вычисления в электротехнике Как

ЛЕКЦИЯ 2 Комплексные вычисления в электротехнике

Как существуют действительные числа с множеством положительных и отрицательных значений, так и комплексные числа имеют множество значени к которым могут применяться те же действия, что и для действительных. Множество действительных чисел расширяется путем присоединения к множеству действительных чисел нового числового объекта - корня уравнения x 2 + 1 = 0. Полученное расширение называется множеством комплексных чисел. Комплексное число обозначается символом a + bi, где a и b - действительные числа, называемые соответственно действительной и мнимой частями, а символ i, определяемый условием i 2 = -1 называется мнимой единицей. Обычно комплексное число обозначают одной буквой, чаще всего z: Действительную и мнимую части комплексного числа обозначают Re z и Im z соответственно: a = Re z, b= Im z

Свойства и определения коплексных чисел . q Два комплексных числа z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i считаются равными (z 1 = z если равны их действительные и мнимые части (a 1 = a 2; b 1 = b 2). q Комплексное число z = a + bi считается равным нулю (z = 0), если его действительная и мнимая части равны нулю (a = b = 0). q Комплексное число z = a + bi при b = 0 считается совпадающим с действительным числом a (a + 0 i = a). q Комплексное число z = a + bi при a = 0 называется чисто мнимым и обозначается bi (0 + bi = bi). q Комплексное число - a 1 - b 1 i называется противоположным комплексному чис a 1 + b 1 i и обозначается - z. q Комплексное число a 1 - b 1 i называется комплексно сопряженным с комплексным числом a 1 + b 1 i и обозначается

Действия над комплексными числами Суммой комплексных чисел z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i называется комплексное число z, действительная часть которого равна сумме действительных частей чисел z 1 и z 2, а мнимая часть - сумме мнимых частей чисел z 1 и z 2 , т. е. . Свойства операции сложения комплексных чисел: ассоциативность: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3); коммутативность: z 1 + z 2 = z 2 + z 1 сумма противоположных комплексных чисел равна нулю: z + (- z) = 0.

Разность комплексных чисел z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i есть комплексное число z, являющееся суммой числа z 1 и числа, противоположного z 2: т. е. комплексное число, действительная и мнимая часть которого равны соответственно разности действительных и мнимых частей уменьшаемого и вычитаемого.

Произведением комплексных чисел называется комплексное число z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i . Появление минуса в правой части обусловлено соотношением: i 2 = - 1. Произведение комплексного числа z = a + bi и комплексно сопряженного с ним чи есть действительное число (a 2 + b 2). Свойства операции умножения комплексных чисел: ассоциативность: (z 1 z 2) z 3 = z 1 (z 2 z 3) коммутативность: z 1 z 2 = z 2 z 1.

Частным двух комплексных чисел z 1 и z 2 (z 2 0) называется такие число z, что . Частное комплексных чисел z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i вычисляется по формуле Число называется модулем комплексного числа z = a + bi. Модуль комплексного числа z = a + bi обозначают z.

ах: Формы записи комплексного числа Комплексное число z может быть представлено в 3 -х формах: -в алгебраической форме: z = a + bi; -в тригонометрической форме: здесь - аргумент. - в показательной форме:

Алгебраическая форма удобна для проведения действий сложения и вычитания. Показательная форма удобна для проведения действий умножения и деления. Тригонометрическая форма является переходной от алгебраической к показательной форме и обратно. При делении и умножении комплексных чисел в показательной форме отдельно проводятся действия с модулями и аргументами. Примеры:

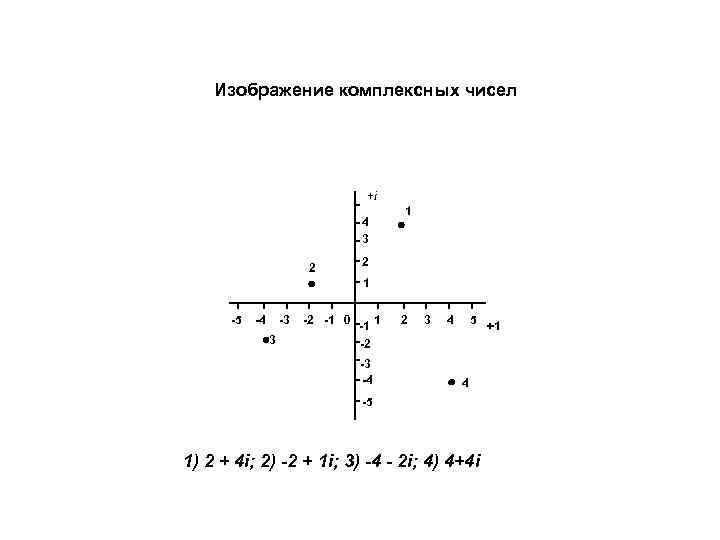Изображение комплексных чисел +i 4 3 2 1 -5 -4 -3 3 -2 -1 0 -1 1 2 3 4 5 +1 -2 -3 -4 4 -5 1) 2 + 4 i; 2) -2 + 1 i; 3) -4 - 2 i; 4) 4+4 i

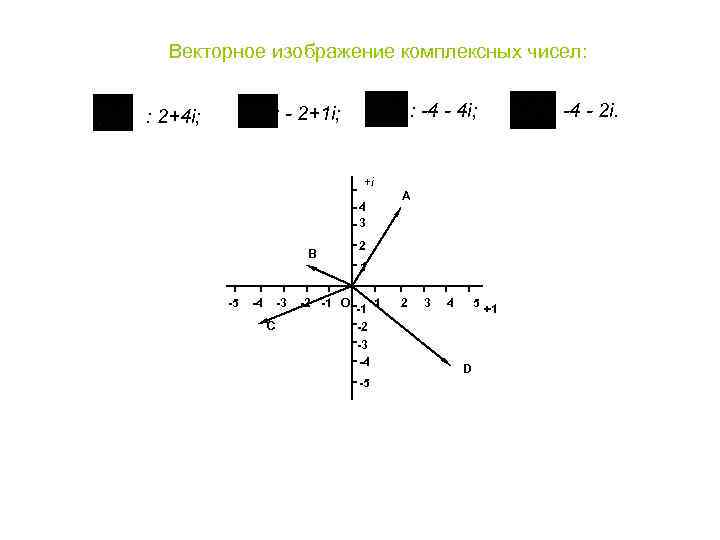Векторное изображение комплексных чисел: : -4 - 4 i; : - 2+1 i; : 2+4 i; +i 4 3 B -5 -4 -3 C A 2 1 -2 -1 O -1 1 -2 -3 -4 -5 2 3 4 5 +1 D : -4 - 2 i.

ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА НА КОМПЛЕКСНОЙ ПЛОСКОСТИ -a + bi = (Acos ) + (Asin )i = Aei +i A b a O +1 Если вектор вращается относительно начала координат со скоростью , то в комплексно форме запись будет выглядеть следующим образом: A[cos( t + ) + i sin( t + )]

Для синусоидальных напряжения и тока с частотой 50 Гц принята запись в комплексной форме: u(t) = Umsin( t + ) U = U ej i(t) = Imsin( t + ) Здесь U I = I ej = Um/ 2 и I = Im/ 2 – действующие значения напряжения и тока В электротехнике i заменено на j, чтобы не отождествлять i (мнимую часть) с мгновенным значением тока Комплекс тока обозначается I, а напряжения - U. Сопряженные комплексы обозначаются соответственно: * I и * U Если I = Iej , то -j. Если U=Uej , то U=Ue-j I=Ie Сопротивление в комплексном виде – Z, проводимость - Y