Лекция 2 Колебания молекул
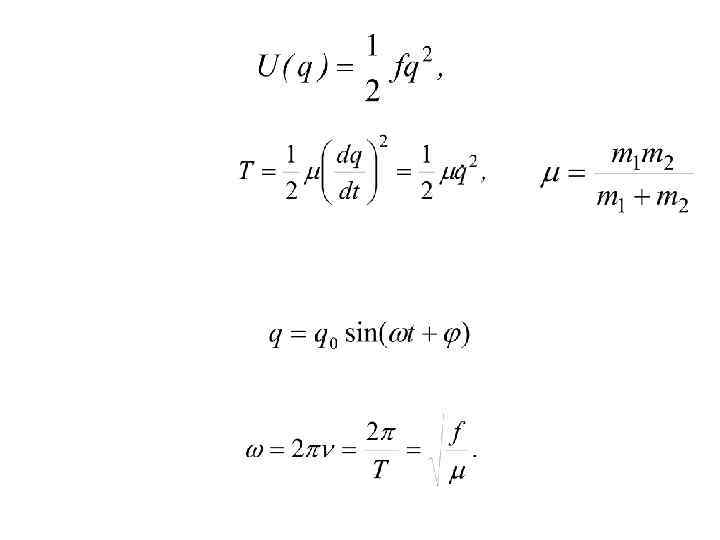
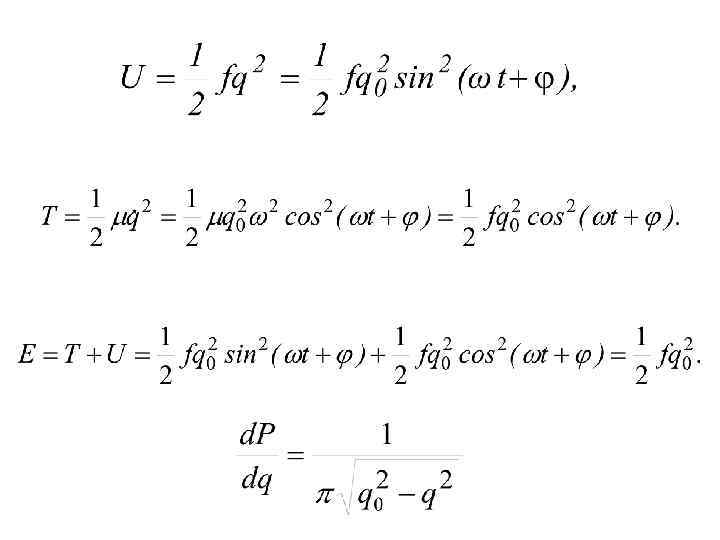
Для квантово-механического решения задачи гармонического осциллятора необходимо найти собственные значения и собственные функции оператора энергии p
Решением уравнение Шредингера собственные значения энергии . собственные функции Nn – нормировочный множитель,
Функции H( ) это полиномы Эрмита степени n (n = 0, 1, 2, 3, 4) H 0( ) = 1 H 1( ) = 2 H 2( ) = 4 2 + 2 H 3( ) = 8 3 12 H 4( ) = 16 4 48 2 + 12
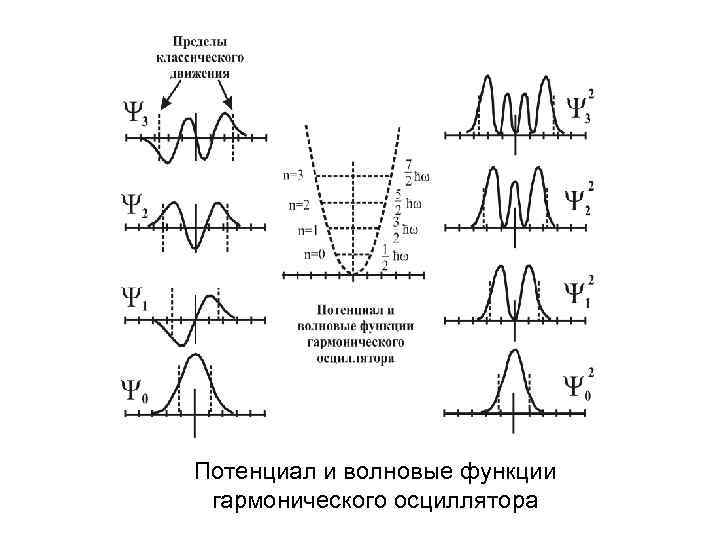
Потенциал и волновые функции гармонического осциллятора
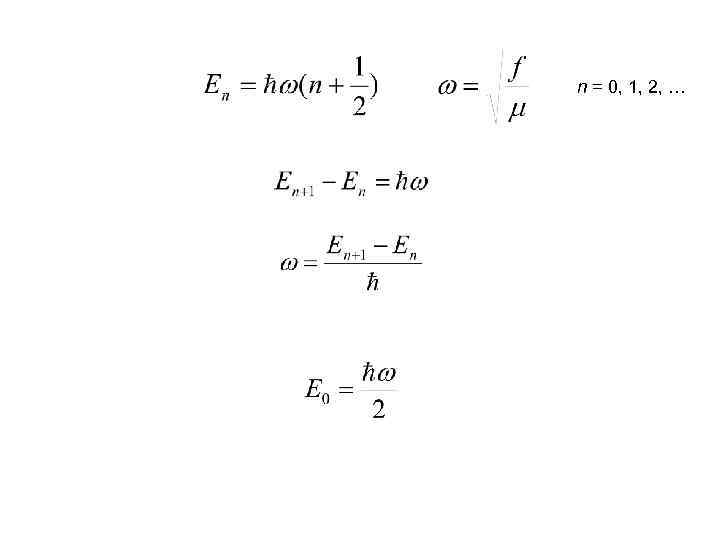
n = 0, 1, 2, …
Амплитуда колебаний: f = 2
для n = 0 имеем
вращательный моментом количества движения Мp J – вращательное квантовое число J = 0, 1, 2, 3, …. момент инерции относительно оси вращения
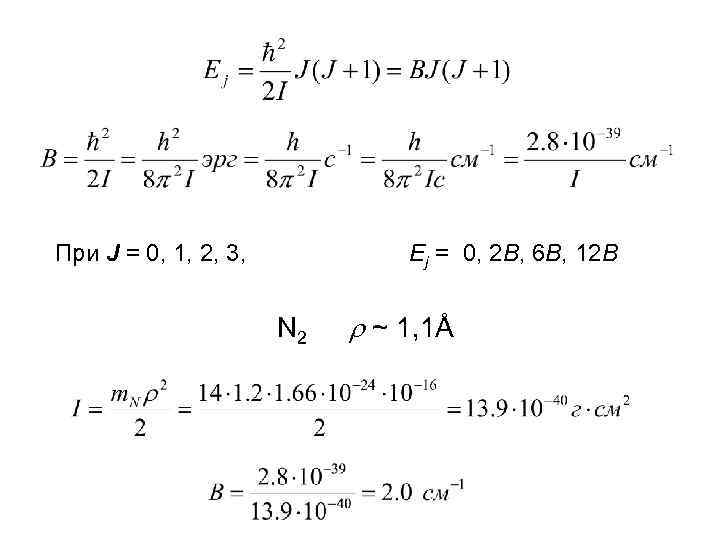
При J = 0, 1, 2, 3, Ej = 0, 2 В, 6 В, 12 В N 2 ~ 1, 1Å
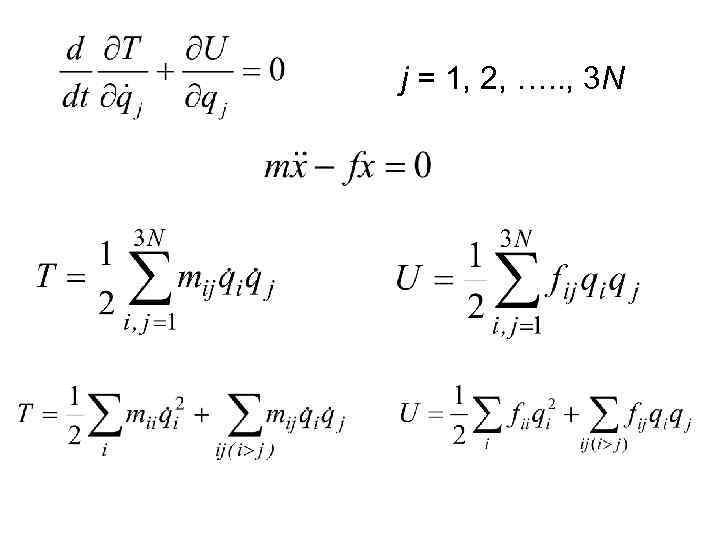
j = 1, 2, …. . , 3 N
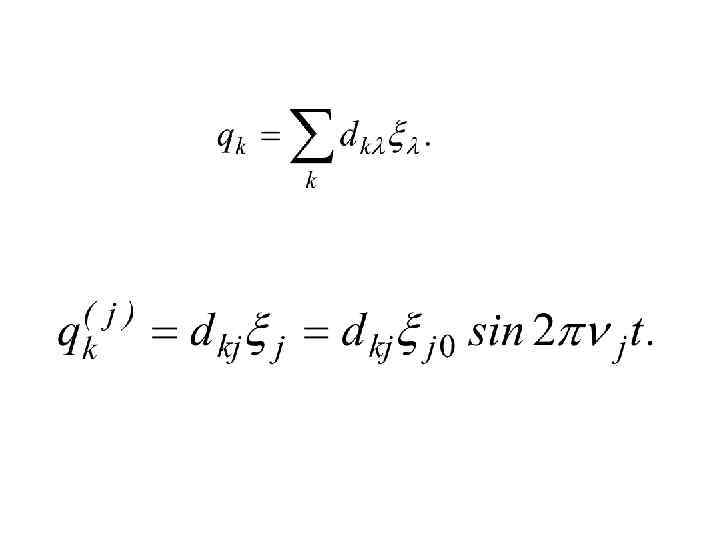
W - E = 0 W = T-1 U T матрица кинематических коэффициентов U матрица силовых постоянных собственное значение
Скачать презентацию Лекция 2 Колебания молекул Для квантово-механического решения
Лекция 2.ppt