ЛЕКЦИЯ 2 ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ

ЛЕКЦИЯ 2

ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД Магнитное поле действует не только на проводники с током, но и отдельные движущиеся заряды. Сила действующая на электрический заряд , движущийся в магнитном поле со скоростью называется: Сила Лоренца Направление силы Лоренца определяется по правилу левой руки. Для положительного заряда (q>0), большой палец указывает направление силы действующей на положительный заряд. Для отрицательного заряда наоборот.

Абсолютное значение Силы Лоренца: α – угол между и. Магнитное поле действует только на движущиеся заряды Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, она изменяет только НАПРАВЛЕНИЕ скорости, но не изменяет её МОДУЛЯ. СИЛА ЛОРЕНЦА НЕ СОВЕРШАЕТ РАБОТЫ. Постоянное магнитное поле не совершает работы над движущейся в ней заряженной частицей, и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

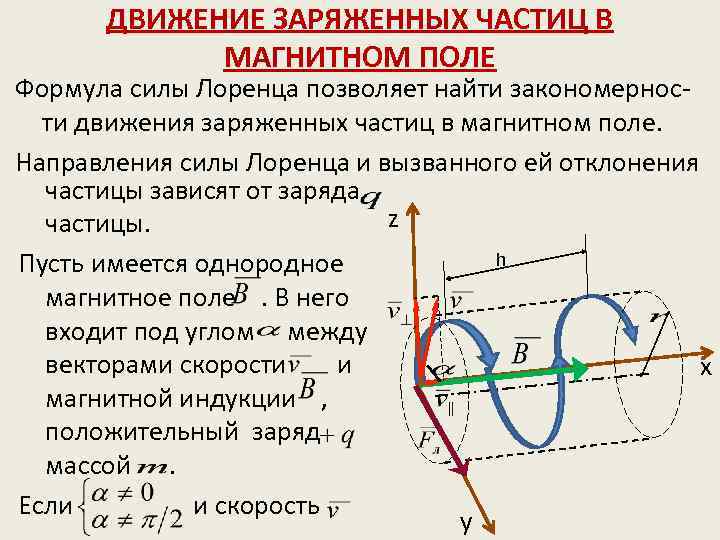ДВИЖЕНИЕ ЗАРЯЖЕННЫХ ЧАСТИЦ В МАГНИТНОМ ПОЛЕ Формула силы Лоренца позволяет найти закономерности движения заряженных частиц в магнитном поле. Направления силы Лоренца и вызванного ей отклонения частицы зависят от заряда z частицы. h Пусть имеется однородное магнитное поле. В него входит под углом между векторами скорости и x магнитной индукции , положительный заряд массой. Если и скорость y

частицы направлена под углом к , то её движение можно представить в виде суперпозиции: 1) Равномерное прямолинейное движение вдоль поля со скоростью 2) Равномерное движение по окружности в плоскости перпендикулярной полю со скоростью. Радиус окружности: В результате сложения обоих движений, возникает движение по спирали, ось которой параллельна магнитному полю. Время затрачиваемое на один полный оборот (Период заряда): Шаг винтовой линии:

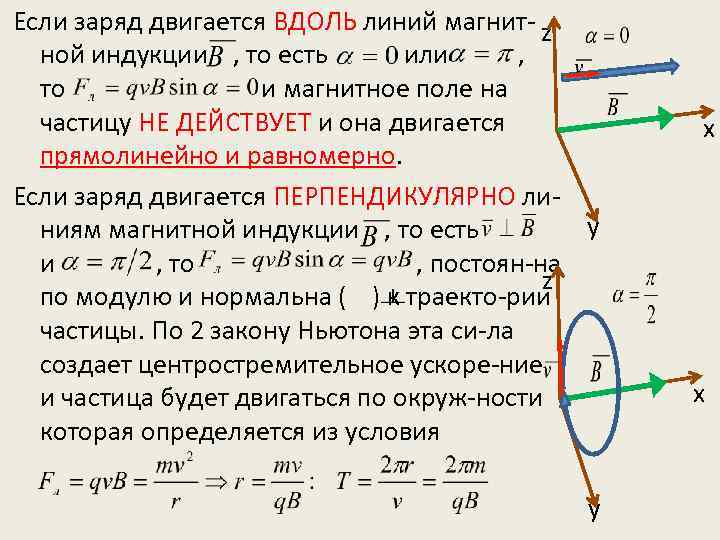Если заряд двигается ВДОЛЬ линий магнит- z ной индукции , то есть или , то и магнитное поле на частицу НЕ ДЕЙСТВУЕТ и она двигается прямолинейно и равномерно. Если заряд двигается ПЕРПЕНДИКУЛЯРНО лиy ниям магнитной индукции , то есть и , то , постоян-на z по модулю и нормальна ( ) к траекто-рии частицы. По 2 закону Ньютона эта си-ла создает центростремительное ускоре-ние и частица будет двигаться по окруж-ности которая определяется из условия y x x

ЭФФЕКТ ХОЛЛА Эффект Холла – возникновение в металле (или полупроводнике) с током плотностью , помещенном в магнитное поле электрического поля в направлении перпендикулярном и. Электроны подвергаются воздействию силы Лоренца и концентрируются у одной из граней металла (эта грань заряжается отрицательно, противоположная положительно). В результате между гранями возникает дополнительное электрическое поле. Когда напряженность этого поля достигнет такой величины, что его действие на заряды, будет уравновешивать силу Лоренца, то установится стационарное

распределение зарядов в поперечном направлении. - поперечная (холловская) разность потенциалов. - концентрация электронов - постоянная Холла( зависит от вещества) Холловская поперечная разность потенциалов прямо пропорциональна магнитной индукции, силе тока, и обратно пропорциональна толщине пластины. По измеренному значению разности потенциалов можно определить концентрацию электронов в веществе. Знак постоянной Холла совпадает со знаком носителя заряда в веществе.

ЦИРКУЛЯЦИЯ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ

Аналогично циркуляции вектора напряженности электростатического поля в вакууме, Циркуляцией вектора по заданному замкнутому контуру называется интеграл - вектор элементарной длины контура, направленной вдоль обхода контура - составляющая вектора в направлении касательной к контуру (с учетом выбранного направления обхода). - угол между векторами и.

ЗАКОН ПОЛНОГО ТОКА ДЛЯ МАГНИТНОГО ПОЛЯ В ВАКУУМЕ (ТЕОРЕМА О ЦИРКУЛЯЦИИ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ) Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов охватываемых этим контуром - число проводников с токами охватываемыми контуром произвольной формы. Циркуляция вектора всегда равна нулю, то есть электростатическое поле является потенциальным, Циркуляция вектора не равна нулю. Магнитное поле – вихревое.

ПРИМЕР ЦИРКУЛЯЦИИ I₃ I₁ I₆ I₂ I₄ I₅ I₇ • Каждый ток учитывается столько раз, сколько он охватывается контуром. • Положительным считается тот ток, направление которого связано с направлением обхода правилом правого винта. • Данное выражение справедливо только для тока в вакууме, так как для полей в веществе необходимо учитывать и молекулярные токи.

МАГНИТНОЕ ПОЛЕ ТОРОИДА И СОЛЕНОИДА

МАГНИТНОЕ ПОЛЕ СОЛЕНОИДА По соленоиду длиной , имеющему витков течет ток. Внутри соленоида магнитное B A поле можно считать однородным, снаружи неоднородным D C и очень слабым. Принято считать что для бесконечно длинного соленоида вся магнитная индукция сосредоточена внутри него, а полем снаружи можно пренебречь. Выберем замкнутый контур ABCDA. Циркуляция вектора по этому контуру будет равна:

Интеграл можно представить как: На участках AB и CD контур перпендикулярен линиям магнитной индукции и. На участке вне контура BC нет магнитной индукции и. На учаастке DA циркуляция вектора равна: Формула магнитной индукции для соленоида

МАГНИТНОЕ ПОЛЕ ТОРОИДА Тороид – кольцевая катушка, витки которой намотаны на сердечник имеющий форму тора. Можно считать что магнитное поле сосредоточено внутри тороида, а вне его отсутствует. Линии магнитной индукции- окружности, центры которых лежат на оси тороида. Если радиус оси тороида , тогда: Значит, внутри тороида магнитная индукция: Вне тороида

ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ ТЕОРЕМА ГАУССА ДЛЯ МАГНИТНОГО ПОЛЯ

ПОТОК ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ Потоком вектора магнитной индукции (магнитным потоком) через площадку называется скалярная физическая величина равная: – проекция вектора на направление нормали к площадке. – вектор модуль которого равен , а направление совпадает с направлением нормали к площадке. – угол между векторами и. Поток вектора может быть как положительным, так и отрицательным (в зависимости от знака ). Обычно поток связывают с контуром правилом правого винта.

Поток вектора через произвольную поверхность равен Для однородного магнитного поля перпендикулярного плоской поверхности получим: Единица измерения магнитного потока: Вебер [Вб]. 1 Вб=1 Тл *м² Один Вебер (1 Вб) – магнитный поток проходящий через плоскую поверхность площадью 1 м², перпендикулярную однородному магнитному полю с индукцией 1 Тл.

ТЕОРЕМА ГАУССА ДЛЯ МАГНИТНОГО ПОЛЯ Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. Для потоков векторов и сквозь замкнутую поверхность в вихревом и потенциальном полях получаются разные значения. Магнитный поток через один виток соленоида площадью S (вокруг сердечника с проницаемостью : Полный магнитный поток (потокосцепление) через витков:

РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА И КОНТУРА С ТОКОМ В МАГНИТНОМ ПОЛЕ

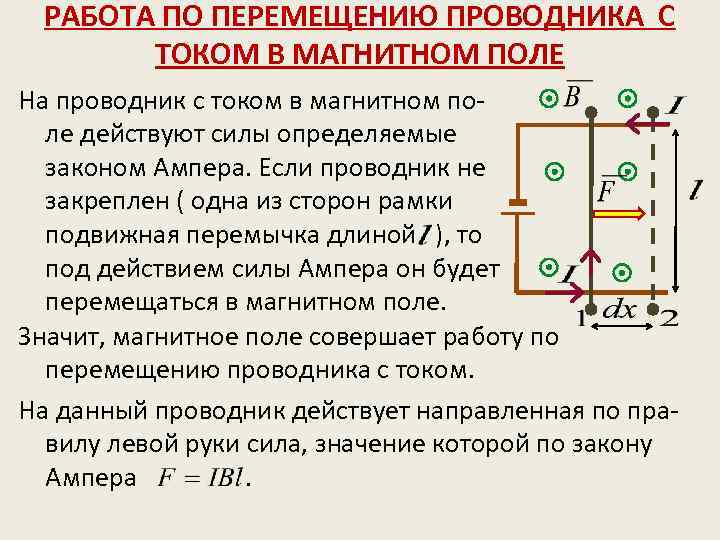РАБОТА ПО ПЕРЕМЕЩЕНИЮ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ На проводник с током в магнитном поле действуют силы определяемые законом Ампера. Если проводник не закреплен ( одна из сторон рамки подвижная перемычка длиной ), то под действием силы Ампера он будет перемещаться в магнитном поле. Значит, магнитное поле совершает работу по перемещению проводника с током. На данный проводник действует направленная по правилу левой руки сила, значение которой по закону Ампера.

под действием этой силы проводник переместится параллельно сам себе из положения 1 в положение 2 на расстояние. Работа совершенная магнитным полем будет равна: – поток вектора магнитной индукции пронизывающий площадь. Работа по перемещению проводника с током магнитным полем равна произведению силы тока протекающего по проводнику на магнитный поток пересеченный проводником.

РАБОТА ПО ПЕРЕМЕЩЕНИЮ КОНТУРА С ТОКОМ В МАГНИТНОМ ПОЛЕ A Пусть контур М с постоянным током перемещается в плоскос. D B М´ ти рисунка и в результате пере- М мещения займет положение М´ C Направление тока по часовой стрелке, магнитного поля перпендикулярно плоскости рисунка. Разобьем контур М на два участка: ABC и CDA. Работа совершаемая силами Ампера по перемещению всего контура, равна алгебраической сумме работ по перемещению проводников ABC( ) и CDA ( ). То есть:

Силы приложенные к участку CDA образуют с направлением перемещения острые углы, поэтому совершаемая ими работа. Эта работа равна произведению силы тока в контуре на пересеченный проводником CDA магнитный поток. Проводник CDA пересекает на своём движении потоки (между начальным и конечным положением) и пронизывающий контур в его конечном положении. Значит: Силы действующие на участок ABC образуют с направлением движения тупые углы и совершаемая ими работа. ABC пересекает при своём движении потоки и пронизывающий контур в его начальном положении. Значит :

Если то: Пусть. – изменение магнитного потока через площадь ограниченную контуром с током. Следовательно: Проинтегрировав это выражение определим работу, совершаемую силами Ампера при конечном произвольном перемещении контура в магнитном поле: Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока сцепленного с контуром. Это справедливо для контура любой формы в произвольном магнитном поле.