Лекция 2 4 часа Волновые процессы Доцент Кравцова

Лекция 2 (4 часа) Волновые процессы Доцент Кравцова О. С.

Волны. Плоская волна. Бегущая и стоячая волны. Фазовая скорость, длина волны, волновое число. Эффект Доплера. Распространение волн в средах с дисперсией. Групповая скорость и ее связь с фазовой скоростью. Нормальная и аномальная дисперсия.

1. Общая характеристика волновых процессов. Волнами называются всякие возмущения состояния вещества или поля, распространяющиеся в пространстве с течением времени. При рассмотрении колебаний не учитывается детальное строение среды; среда рассматривается как сплошная, непрерывно распределенная в пространстве и обладает упругими свойствами. Среда называется линейной, если ее свойства не изменяются под действием возмущений, создаваемых колебаниями. Волна – это процесс распространения колебаний в сплошной среде. При распространении волны частицы колеблются около своих положений равновесия, а не перемещаются вслед за волной. Вместе с волной от частицы к частице передается только состояние колебательного движения и его энергия. Основным свойством всех волн является перенос энергии без переноса вещества. Волна, в отличие от колебаний, характеризуется периодичностью не только во времени, но и в пространстве.

Временнáя периодичность волны Временной период волны. Если в моменты времени 1 и 2 происходят колебания в фазе, т. е. то , где Т – период волны.

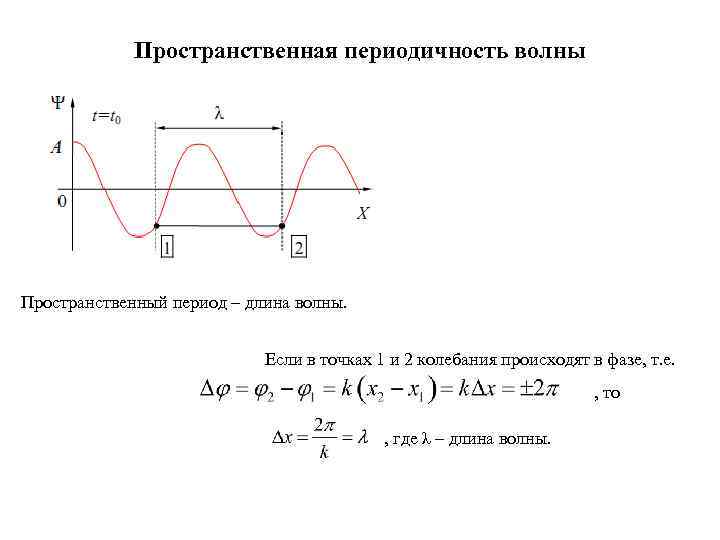Пространственная периодичность волны Пространственный период – длина волны. Если в точках 1 и 2 колебания происходят в фазе, т. е. , то , где λ – длина волны.

Основное понятие волнового движения – фронт волны. Фронт волны – волновая поверхность, отделяющая возмущенную область пространства от невозмущенной. В однородном и изотропном пространстве форма фронта определяется формой источника. Примеры:

Виды волновых процессов: 1. Механические волны; 2. Электромагнитные волны (колебания векторов напряженности электрического и индукции магнитного полей, распространяющиеся в пространстве). В отличие от механических, могут распространяться в вакууме.

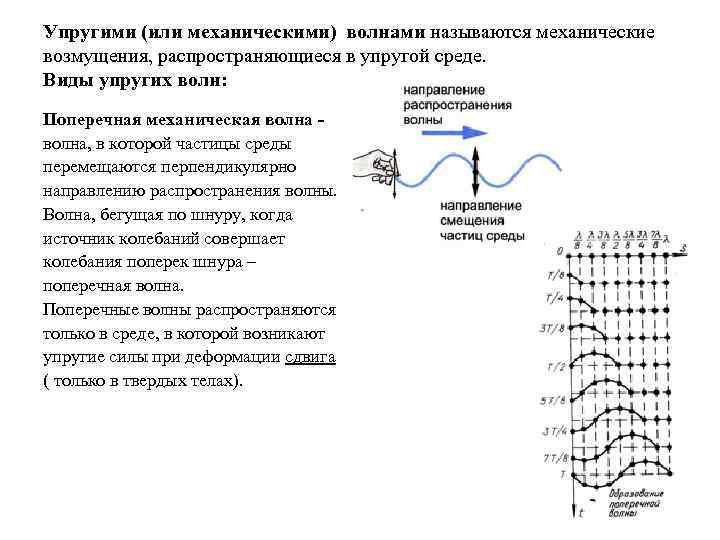Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Виды упругих волн: Поперечная механическая волна, в которой частицы среды перемещаются перпендикулярно направлению распространения волны. Волна, бегущая по шнуру, когда источник колебаний совершает колебания поперек шнура – поперечная волна. Поперечные волны распространяются только в среде, в которой возникают упругие силы при деформации сдвига ( только в твердых телах).

Продольная волна - волна, в которой движение частиц среды происходит вдоль направления распространения волны. Когда источник колебаний совершает колебания вдоль пружины - разряжения и сжатия, бегущие вдоль пружины, представляют продольную волну. Продольные волны могут распространяться в средах, в которых возникают упругие силы при деформации сжатия и растяжения (в твердых, жидких и газообразных телах).

Хорошей моделью образования волны в шнуре может служить цепочка маленьких шариков, между которыми действует сила упругости (на рисунке изображены пружинки). Поперечная волна:

Упругая волна называется гармонической, если соответствующие ей колебания частиц среды происходят по гармоническому закону. На рис. 1 приведена гармоническая поперечная волна, распространяющаяся со скоростью вдоль оси x. . В . О Рис. 1 Расстояние между ближайшими частицами, колеблющимися в одинаковых фазах, называется длиной волны , то есть длина волны – это расстояние, на которое определенная фаза колебаний распространяется за один период колебания: где u – фазовая скорость волны, то есть скорость распространения данной фазы колебания. Отличие графика волны от графика гармонического колебания: 1)график волны представляет зависимость смещения всех частиц среды от расстояния до источника колебаний в данный момент времени 2)график гармонического колебания это зависимость смещения данной частицы от времени

2. Уравнение бегущей волны. Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии в волнах количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (поимени русского ученого Н. А. Умова (1846 -1915 гг), решившего задачу о движении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны. Важными примерами бегущих волн являются плоская и сферическая волны. Волна называется плоской, если ее волновые поверхности представляют совокупность плоскостей, параллельных другу. Волна называется сферической, если ее волновые поверхности имеют вид концентрических сфер. Центры этих сфер называются центром волны.

У мов Никола й Алексе евич Дата рождения: 23 января (4 февраля) 1846 г. Место рождения: Симбирск Дата смерти: 15 (28) января 1915 г. (68 лет) Место смерти: Москва Страна: Российская империя Научная сфера: Физика Место работы: МГУ имени М. В. Ломоносова Известный ученик: А. В. Цингер

«Моментальные фотографии» бегущей синусоидальной волны в момент времени t + Δt.

Пусть точка В среды находится на расстоянии х от источника колебаний О(рис. 1). Колебания точек среды описываются функцией Колебания точки В отстают по времени от колебаний источника на величину Уравнение колебаний частиц, лежащих в плоскости х, будет иметь вид: Это уравнение представляет собой уравнение бегущей волны. В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию (А=const), имеет вид: , Учитывая, что и , получим где k – волновое число.

Волновое число показывает, сколько длин волн укладывается на расстоянии, равном. Тогда уравнение плоской волны можно записать в виде Скорость распространения фазы волны называется фазовой скоростью. Пусть в волновом процессе фаза постоянна Уравнение сферической волны

Найдем вторые производные от по переменным t и х: Это уравнение плоской волны, распространяющейся вдоль оси х. волновое уравнение оператор Лапласа.

3. Принцип суперпозиции. Если среда, в которой распространяется одновременно несколько волн, линейна, то к этим волнам применим принцип суперпозиций (наложения) волн: При распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвующие в каждом из слагаемых волновых процессов.

4. Интерференция волн. Когда источники колебаний колеблются с одинаковой частотой, имеют одинаковые направления колебаний и постоянную во времени разность фаз. Такие источники называются когерентными. Две волны называются когерентными, если разность их фаз не зависит от времени. Интерференцией волн называется явление наложения волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других в зависимости от соотношения между фазами этих волн. . В Рис. 2

Амплитуда результирующего колебания будет максимальной во всех точках В, для которых аргумент косинуса равен четному числу : где Если заменить и принять, что , то Это соотношение выражает условие интерференционного максимума: максимум амплитуды колебаний получается в точках пространства, для которых разность хода волн равна нулю или целому числу длин волн. Целое число m называется порядком интерференционного максимума.

Амплитуда результирующего колебания будет минимальной во всех точках В, для которых где , откуда (при ) получаем условие интерференционного минимум то есть минимум амплитуды колебаний получается в точках пространства, для которых разность хода волн равна нечетному числу длин полуволн. Число m в данном случае называется порядком интерференционного минимума.

5. Стоячие волны – это волны, образующиеся в результате наложения двух встречных плоских волн с одинаковыми амплитудами и частотами. Уравнение стоячей волны: пучности стоячей волны узлы стоячей волны (координаты пучностей) (координаты узлов)

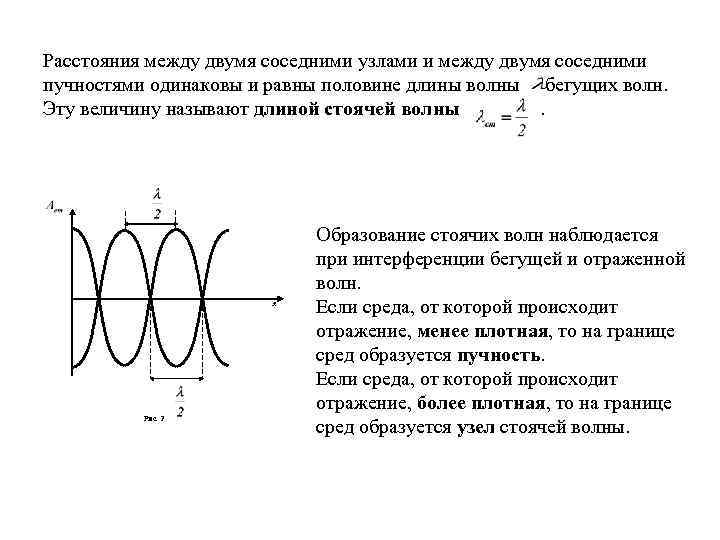Расстояния между двумя соседними узлами и между двумя соседними пучностями одинаковы и равны половине длины волны бегущих волн. Эту величину называют длиной стоячей волны. х Рис. 2 Образование стоячих волн наблюдается при интерференции бегущей и отраженной волн. Если среда, от которой происходит отражение, менее плотная, то на границе сред образуется пучность. Если среда, от которой происходит отражение, более плотная, то на границе сред образуется узел стоячей волны.

6. Групповая скорость. Дисперсия. Явление зависимости скорости распространения волны от частоты называется дисперсией. Возьмем две гармонические волны с одинаковыми амплитудами, близкими частотами и волновыми числами. Групповой скоростью называется скорость движения группы волн, образующих в каждый момент времени, локализованный в пространстве волновой пакет (или скорость движения центра волнового пакета). Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства. Найдем связь групповой и фазовой скоростей: нормальная дисперсия аномальная дисперсия

7. Эффект Доплера. Эффектом Доплера (Х. Доплер, австрийский физик и математик, XIX в. ) называют изменение частоты колебаний, воспринимаемых приемником, при движении источника этих колебаний и приемника друг относительно друга. Пусть источник и приемник звука движутся вдоль соединяющей их прямой: – скорости движения источника и приемника (положительны при сближении и отрицательны при удалении источника и приемника); – частота колебаний источника; – скорость распространения звука в данной среде.

1. Источник и приемник покоятся относительно среды 2. Приемник приближается к источнику, источник покоится 3. Источник приближается к приемнику, приемник покоится . . Рис. 3 4. Источник и приемник движутся друг относительно друга. Верхний знак берется, если при движении источника или приемника происходит их сближение, нижний знак – в случае их взаимного удаления.

Кристиан Доплер - австрийский физик. Дата рождения: 29 ноября 1803 г Место рождения: Зальцбург Дата смерти: 17 марта 1853 г (49 лет) Место смерти: Венеция Научная сфера: физика (оптика и акустика) Место работы: Чешский технический университет, Венский университет

Продольные волны в твердом теле. Энергетические соотношения. Вектор Умова. Упругие волны в газах и жидкостях. Плоские электромагнитные волны. Вектор Пойтинга. Волновая и геометрическая оптика.

1. Диапазон звуковых волн Акустика – область физики, в которой изучаются звуковые волны. Звуковые (акустические) волны – упругие волны с частотами от 16 Гц до 20 к. Гц, распространяющиеся в среде и воспринимаемые органами слуха человека (границы условны, то есть для разных людей они различны). Инфразвуковые волны – звуковые волны с частотами ниже границ диапазона восприятия уха человека, то есть меньше 16 Гц. Ультразвуковые волны – звуковые волны с частотами выше границ диапазона восприятия уха человека, то есть больше 20 к. Гц. В жидкостях и газах они могут быть только продольными, так как эти среды обладают упругостью лишь по отношению к деформациям сжатия (растяжения). В твердых телах они могут быть как продольными, так и поперечными, поскольку твердые тела обладают упругостью по отношению к деформациям сжатия (растяжения) и сдвига.

2. Характеристики звука • • • Интенсивность (сила) I звука – энергетическая характеристика – величина, определяемая средней по времени энергией, переносимой звуковой волной в единицу времени сквозь площадку, ориентированную перпендикулярно направлению распространению волны. Громкость звука – субъективная характеристика – величина, характеризующая слуховое ощущение для данного звука и зависящая от интенсивности звука, частоты и формы звуковых колебаний. Уровень интенсивности звука – объективная оценка громкости звука Уровень громкости – физиологическая характеристика – выражается в фонах (фон). Громкость для звука 1000 Гц (частота стандартного чистого тона (синусоидального гармонического колебания)) равна 1 фон, если его уровень интенсивности равен 1 д. Б. Высота звука – субъективная характеристика – качество периодического или почти периодического звука, определяемое человеком на слух и зависящее от частоты звука. С повышением частоты высота звука увеличивается (звук становится «выше» ), с уменьшением частоты – понижается.

3. Скорость звука в различных средах Скорость звука в газах Скорость звука в изотропных твердых телах Скорость звука в твердых телах значительно больше, чем в жидкостях и газах, так как упругость значительно больше. Скорость звука в жидкостях

4. Электромагнитные волны Существование электромагнитных волн было теоретически предсказано великим английским физиком Дж. Максвеллом в 1864 году. Электромагнитные волны – это переменное электромагнитное поле, распространяющееся в пространстве с конечной скоростью. Существование электромагнитных волн вытекает из уравнений Максвелла которые в области пространства, не содержащей свободных электрических зарядов и макроскопических токов, имеют вид

Если среда – однородный и изотропный диэлектрик, не обладающий сегнетоэлектрическими или ферромагнитными свойствами, то В этом случае Волновые уравнения для векторов Скорость электромагнитных волн в вакууме : Скорость c распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных. Электромагнитные поля действительно могут существовать в виде электромагнитных волн. Поскольку , то - скорость распространения электромагнитных волн в веществе всегда меньше, чем в вакууме.

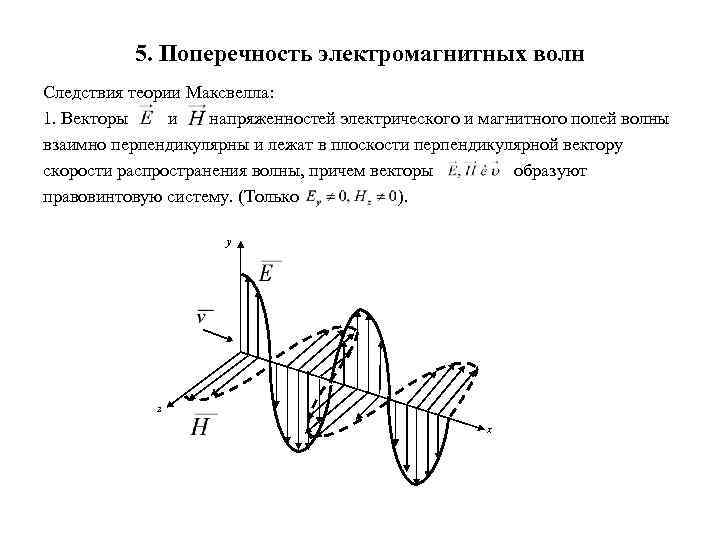5. Поперечность электромагнитных волн Следствия теории Максвелла: 1. Векторы и напряженностей электрического и магнитного полей волны взаимно перпендикулярны и лежат в плоскости перпендикулярной вектору скорости распространения волны, причем векторы образуют правовинтовую систему. (Только ). y z x

2. В электромагнитной волне векторы одинаковых фазах. и всегда колеблются в Следовательно, Е и Н одновременно достигают максимума, одновременно обращаются в нуль и так далее. Волновым уравнениям удовлетворяют плоские монохроматические волны, которые Описываются следующими уравнениями:

6. Энергия электромагнитных волн Вектор направлен в сторону распространения электромагнитной волны, а его модуль равен энергии, переносимой электромагнитной волной за единицу времени через единичную площадку, перпендикулярную направлению распространения волны. Интенсивность волны Своим направлением вектор определяет направление переноса энергии.

Джон Генри Пойнтинг — известный британский физик. Дата рождения: 9 сентября 1852 г Место рождения: Манчестер, Великобритания Дата смерти: 30 марта 1914 г (61 год) Место смерти: Бирмингем, Великобритания Страна: Великобритания Научная сфера: физика Место работы: Бирмингемский университет Известные ученики: Фрэнсис Уильям Астон Известен как: вектор Умова Пойнтинга, эффект Пойнтинга, теорема Пойнтинга, эффект Пойнтинга-Робертсона Награды и премии: Премия Адамса (engl. ) (1893 г), Королевская медаль (engl. ) (1905 г)

Волновая и геометрическая оптика. Оптика – раздел физики, который изучает природу света, световые явления и взаимодействие света с веществом. Оптику делят на: - Геометрическую (лучевую) - Волновую (физическую) - Квантовую (корпускулярную)

Основные законы геометрической оптики • Закон прямолинейного распространения света – свет в оптически однородной среде распространяется прямолинейно. • Закон независимости световых пучков – эффект, производимый отдельным пучком, не зависит от того, действуют ли одновременно остальные пучки или они устранены. • Закон отражения – отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, проведенном к границе раздела двух сред в точке падения; луч отражения равен углу падения:

• Закон преломления – луч падающий, луч преломленный и перпендикуляр, проведенный к границе раздела двух сред в точке падения, лежат в одной плоскости; отношение синуса угла падения к синусу угла преломления есть величина постоянная для данных сред. относительный показатель преломления второй среды относительно первой, который равен отношению абсолютных показателей преломления двух сред. - Абсолютный показатель преломления среды называется величина, равная отношению скорости электромагнитных волн в вакууме к их фазовой скорости в среде.

8. Полное отражение. Если свет распространяется из среды с большим показателем преломления (оптически более плотной) в среду с меньшим показателем преломления (оптически менее плотную) ( например, из стекла в воздух или из воды в воздух), то При углах падения весь падающий свет полностью отражается. Это явление называется полным внутренним отражением света. Предельный угол определяется соотношением:

9. Энергетические величины в фотометрии Фотометрия – раздел оптики, в котором рассматривают энергетические характеристики оптического излучения в процессах его испускания, распространения и взаимодействия с веществом. Энергетические величины в фотометрии – характеризуют энергетические параметры оптического излучения без учета особенностей его воздействия на тот или иной приемник излучения. • Поток излучения - величина, равная отношению энергии излучения ко времени, за которое излучение произошло (мощность излучения). • Энергетическая светимость (излучательность) - величина, равная отношению потока излучения, испускаемого поверхностью, к площади сечения, сквозь которое этот поток происходит (поверхностная плотность потока излучения). • Энергетическая сила света (сила излучения) – величина, равная отношению потока излучения точечного источника к телесному углу, в пределах которого это излучение распространяется.

• Энергетическая яркость (лучистость) – величина, равная отношению энергетической силы света элемента излучающей поверхности к площади проекции этого элемента на плоскость, перпендикулярную направлению наблюдения. • Энергетическая освещенность (облученность) характеризует величину потока излучения, падающего на единицу освещаемой поверхности.