
Лекція № 2 (3) Багатошарові композити
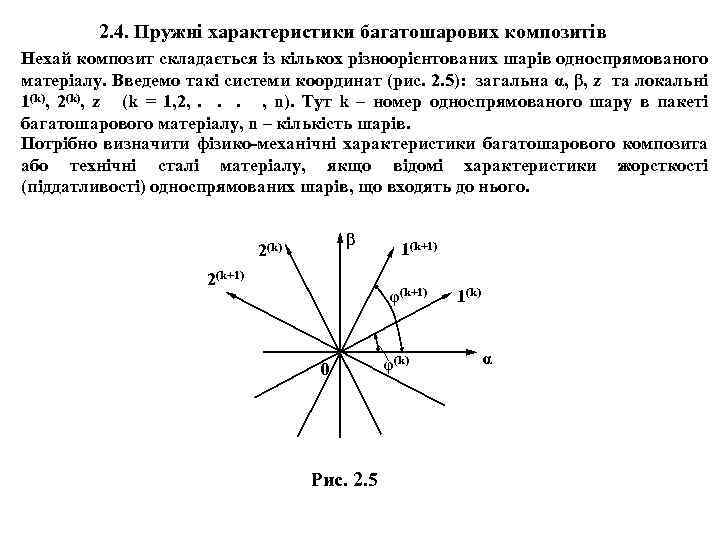
2. 4. Пружні характеристики багатошарових композитів Нехай композит складається із кількох різноорієнтованих шарів односпрямованого матеріалу. Введемо такі системи координат (рис. 2. 5): загальна α, β, z та локальні 1(k), 2(k), z (k = 1, 2, . . . , n). Тут k – номер односпрямованого шару в пакеті багатошарового матеріалу, n – кількість шарів. Потрібно визначити фізико-механічні характеристики багатошарового композита або технічні сталі матеріалу, якщо відомі характеристики жорсткості (піддатливості) односпрямованих шарів, що входять до нього. β 2(k) 2(k+1) 1(k+1) φ(k+1) 0 Рис. 2. 5 φ(k) 1(k) α

2. 4. 1. Пружні характеристики багатошарових композитів (плоский напружений стан). Розглянемо паралелепіпед одиничної довжини та ширини (рис. 2. 6). Внутрішні зусилля визначаються із таких співвідношень рівноваги: z Tα (k ) H h Tαβ (2. 68) α де n – кількість шарів у пакеті; Tα β нормальне напруження в k-шарі у напрямі осі α; нормальне напруження в k-шарі Рис. 2. 6 у напрямі осі β; дотичне напруження в k-шарі у площині α 0β. Якщо розділити праві й ліві частини рівняння (2. 68) на сумарну товщину пакета Tαβ отримаємо (2. 69) де середні по товщині пакета напруження, які дорівнюють відносна товщина k-шару.

Підставивши у співвідношення (2. 69) закон Гука для k-шару (2. 57) – (2. 58) у вигляді (2. 70) (2. 71) і враховуючи те, що отримаємо рівняння зв’язку середніх напружень із середніми деформаціями багатошарового матеріалу при плоскому напруженому стані: (2. 72) де або (2. 72*) (2. 73) Для визначення технічних сталих пружності багатошарового композита можна розглянути деформацію розтягання такого композита у напрямі осі α. Рівняння (2. 72*) при цьому набере вигляду (2. 74) Записавши і із двох останніх рівнянь (2. 74) як функції їх у перше рівняння системи (2. 74), отримаємо і підставивши

(2. 75) У формулі (2. 75) (2. 75*) мінор елемента матриці (2. 75**) визначник матриці Аналогічним шляхом знаходять інші значення технічних сталих (2. 76) (2. 77) а також коефіцієнти Пуассона (2. 78) У випадку ортотропного композита, якщо формули типу (2. 42): отримаємо вже відомі (2. 79) Із рівнянь (2. 72) – (2. 73) безпосередньо дістанемо висновок, що порядок чергування шарів у пакеті багатошарового матеріалу не має значення при підрахунку його жорсткості.