Лекция 2 2 ОСНОВЫ РАССЕЯНИЯ ВЕЩЕСТВ В АТМОСФЕРЕ 1

Лекция 2/2. ОСНОВЫ РАССЕЯНИЯ ВЕЩЕСТВ В АТМОСФЕРЕ 1. Виды источников загрязнений. 2. Уравнение турбулентной диффузии. 3. Определение вероятности поражения людей при химических авариях.

1. Виды источников загрязнений. При решении задач, связанных с защитой населения при химических авариях, важной проблемой является адекватная оценка пространственно-временных масштабов воздействия поражающих факторов в основном в виде ингаляционных токсических нагрузок. Прогнозирование ингаляционных поражений населения в настоящее время является наиболее развитым направлением. Оно основывается на построении полей концентраций АХОВИД в приземном слое воздуха толщиной до 50 метров, в котором проявляется механическое и тепловое воздействие подстилающей земной поверхности на воздушное течение.

Основной причиной рассеивания вредных веществ является турбулентность воздуха в атмосфере. В верхней части приземного слоя воздуха наблюдается крупномасштабная турбулентность, близкая к однородной (т. е. нет выделенных точек, которые отличались бы от других) и изотропной (т. е. одинаковость свойств пространства по всем направлениям), вызванная взаимодействием различных течений воздуха. В нижней части приземного слоя - турбулентность, сравнительно мелкомасштабная, генерируемая в основном обтеканием ветром строений, шероховатостью подстилающей поверхности (земли), а также рельефом местности.

В зависимости от высоты (Н) устья источника выброса вредного вещества над уровнем земной поверхности, делятся на четыре класса: высокие, Н 50 м; средней высоты, Н = 10… 50 м; низкие, Н = 2… 10 м; наземные, Н 2 м.

При авариях на ХОО источники химического заражения в зависимости от сценария аварии, характера разрушения технологического оборудования и пожарной обстановки могут относиться к любому из перечисленных классов. Так, при проливе АХОВИД на землю источник химического заражения приземного слоя воздуха следует рассматривать как наземный. При аварийной разгерметизации оборудования или факельном выбросе, когда образуется только первичное облако зараженного воздуха, выбрасываемое вверх, источник химического заражения может быть, в зависимости от высоты выброса, отнесен к низким или средней высоты. В тех случаях, когда авария сопровождается сильным пожаром с образованием конвективной колонки, часть АХОВИД может быть увлечена восходящим горячим потоком воздуха вверх и в результате образовать высокий источник химического заражения.

Для высоких и средних источников, если их высота более 3, 5 Нзд (Нзд - высота зданий возле источника выброса), влиянием на распространение примесей деформации ветрового потока, вызванной строениями, можно пренебречь. Определяющей при этом является турбулентность самой атмосферы. Для низких и наземных источников влиянием на рассеяние АХОВИД зданий, расположенных в непосредственной близи от них, пренебрегать нельзя. Это необходимо учитывать при построении полей концентраций АХОВИД.

По температуре поступающей в атмосферу газо-воздушной смеси выбросы можно подразделить на сильно нагретые ( t 100 0 С), нагретые (20 0 С < t 100 0 C), слабо нагретые (5 0 С < t 20 0 C), изотермические ( t = 0) и охлажденные ( t <0). Где t - разница между температурами выброса и окружающей среды Авариям на ХОО будут характерны в основном: сильно нагретые и нагретые (при пожарах), изотермические (при разгерметизации складских, транспортных емкостей с АХОВИД, хранящиеся при температуре окружающей среды под небольшим избыточным давлением) и охлажденные (для изотермических хранилищ сжиженных газов, сжатых газо-воздушных смесей).

При описание полей концентраций (в зависимости от постановки задачи) используются следующие математические модели: мгновенного точечного источника (МТИ); мгновенного объемного источника (МОИ); постоянно действующего точечного источника (ПДТИ); постоянно действующего площадного источника (ПДПИ); постоянно действующего линейного источника (ПДЛИ); рассеяния облаков тяжелых газов; рассеяния в условиях штиля и слабого (до 0, 5 м/с) ветра; рассеяния в условиях образования конвективной колонки при пожарах.

Условиями использования той или иной модели являются, в первую очередь, глубина распространения поражающих факторов и удаленность объекта поражения, а также его размеры (по сравнению с размерами самого источника химического заражения) и время действия источника (или образования того или иного вида поражающего фактора). Распределение выбросов на мгновенный и постоянный производится по следующим условиям для мгновенного выброса ; (1) . (2) для постоянного выброса где х- расстояние от места выброса; u – скорость ветра, м/с; tв – время выброса, с.

Применение модели точечного предлагается в тех случаях, когда источника , (3) где: х - расстояние от источника выброса по оси Х; R - параметр начального разброса, например, радиус облака.

Для площадного источника условиями рассмотрения вида источника выбраны: ; (4) , (5) одиночный источник где: х - расстояние от центра площадного источника до расчетной точки, м; S - площадь источника, м 2; u - расчетная скорость ветра, м/с; 5 - размерный коэффициент, (м/с)-0, 5.

Для рассмотрения источника загрязнения как линейного используется следующее условие: (6) , где: х - наименьшее расстояние от источника до расчетной точки на местности, м; L - длина линейного источника, м; u - расчетная скорость ветра, м/с.

Исходя из особенностей химических аварий, при прогнозировании пространственно временных масштабов химического заражения методический аппарат, как правило, должен быть ориентирован на описание полей концентраций: от низких и наземных источников изотермических и охлажденных выбросов с учетом влияния шероховатости подстилающей поверхности и наличия в непосредственной близи от источника химического заражения зданий и сооружений; а при радиационных авариях: от высоких источников сильно нагретых выбросов с учетом отражения примеси от поверхности земли. При этом влиянием местности и городской застройки на распространение вредных веществ можно пренебречь.

Первые попытки теоретического описания процесса диффузии примеси в атмосфере были предприняты Г. И. Тейлором в 1915 г. и В. Шмидтом в 1917 г. В 1932 г. была опубликована работа О. Г. Сэттона, в которой изложена теория рассеивания примесей, основанная на статистической теории турбулентности. Дальнейшее развитие теории рассеивания шло в основном по двум направлениям: решения, полученные из уравнения турбулентной диффузии с переменными коэффициентами, и решения, полученные на основе статистической теории.

В настоящее время для расчета промышленных загрязнений наиболее употребительны два подхода: первый разработан М. Е. Берляндом в Главной геофизической обсерватории СССР для расчета рассеивания в атмосфере вредных веществ, содержащихся в выбросах предприятий; второй - Ф. Пасквиллом для оценки загрязнения атмосферы от предприятий атомной промышленности и энергетики.

Наиболее полно процессы поведения загрязняющих веществ в приземном слое воздуха на высоте до нескольких метров исследованы в военном деле при оценке эффективности действия химического оружия. Профессорами Чернушевичем Л. М. , Калитаевым Л. Н. , Киреевым А. В. , Батыревым В. В. были разработаны теоретические основы и проведено математическое моделирование поражающего действия и эффективности применения вероятным противником химического оружия. В результате были получены математические соотношения, позволяющие рассчитывать мощность поражающего действия химического оружия, которые были положены в основу при разработке соответствующих методик.

Таким образом, в настоящее время теория диффузии примесей в атмосфере при отсутствии препятствий разработана достаточно полно. Несмотря на многообразие формул, все они могут быть получены из одного дифференциального уравнения турбулентной диффузии. Результаты расчетов по формулам совпадают при соответствующем подборе экспериментальных констант.

2. Уравнение турбулентной диффузии. Скорость массопередачи связана с механизмом переноса распределяемого вещества в фазах, между которыми происходит массообмен. Перенос вещества внутри фазы (мы рассматриваем газообразные и жидкие среды) может происходить только путем молекулярной диффузии либо путем конвекции и молекулярной диффузии одновременно, разновидностью которой является турбулентная диффузия.

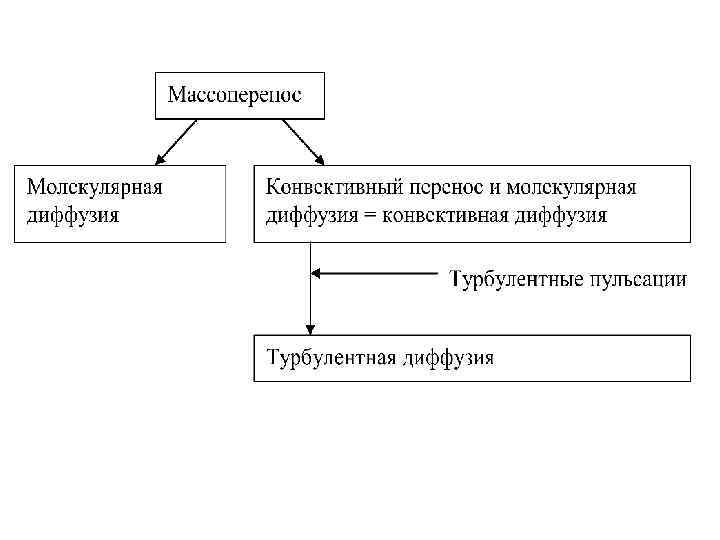
Молекулярная диффузия. Молекулярной диффузией называется перенос распределяемого вещества, обусловленный беспорядочным движением самих молекул. Молекулярная диффузия описывается первым законом Фика, согласно которому количество вещества d. M, продиффундировавшего за время dt через элементарную поверхность d. F (нормальную к направлению диффузии) пропорционально градиенту концентрации d. C/dх этого вещества: (6) или , (7) ,

Из выражения (7) следует, что удельный поток вещества, переносимого молекулярной диффузией через единицу поверхности (F = 1) в единицу времени (t = 1), или скорость молекулярной диффузии, составляет (8) , По своей структуре закон Фика аналогичен закону Фурье, описывающему передачу тепла теплопроводностью, причем аналогом градиента температур является в данном случае градиент концентрации, представляющий собой изменение концентрации диффундирующего вещества на единицу длины нормали между двумя поверхностями постоянных, но различных концентраций.

Коэффициент пропорциональности D в выражении закона Фика называется коэффициентом молекулярной диффузии, или просто коэффициентом диффузии. Знак минус перед правой частью первого закона Фика указывает на то, что молекулярная диффузия всегда протекает в направлении уменьшения концентрации распределяемого компонента. Согласно уравнению (8), коэффициент диффузии выражается следующим образом: (9) , Физический смысл D Коэффициент диффузии показывает какое количество вещества диффундирует в единицу времени через единицу поверхности при градиенте концентрации, равном единице.

Коэффициент молекулярной диффузии представляет собой физическую константу, характеризующую способность данного вещества проникать вследствие диффузии в неподвижную среду. Величина D таким образом не зависит от гидродинамических условий, в которых протекает процесс. Значения коэффициента диффузии являются функцией свойств распределяемого вещества, свойств среды, через которую оно диффундирует, температуры и давления. Обычно величины D возрастают с увеличением температуры и понижением давления (для газов). В каждом конкретном случае значение D определяют по опытным данным или по теоретическим и полуэмпирическим уравнениям с учетом температуры и давления, при которых протекает процесс диффузии. Коэффициенты диффузии газа в среду другого газа имеют значения 0, 1— 1 см 2/сек, а при диффузии газа в жидкость они в 104 — 105 раз меньше и составляют примерно 1 см 2/сутки. Таким образом, молекулярная диффузия является весьма медленным процессом, особенно в жидкостях.

Турбулентная диффузия. Количество вещества d. Mт, переносимого в пределах фазы вследствие турбулентной диффузии, принимается, по аналогии с молекулярной диффузией, пропорциональным поверхности d. F, времени dt и градиенту концентрации d. C/dх и определяется по уравнению (10) , где — коэффициент турбулентной диффузии.

Соответственно удельный поток вещества, переносимого путем турбулентной диффузии через единицу поверхности в единицу времени, или скорость турбулентной диффузии, составляет (11) , где - коэффициент турбулентной диффузии показывает, таким образом, какое количество вещества передается посредством турбулентной диффузии в единицу времени через единицу поверхности при градиенте концентрации, равном единице. Коэффициент выражается в тех же единицах, что и коэффициент молекулярной диффузии, т. е. в м 2/сек. Однако в отличие от D коэффициент турбулентной диффузии не является физической константой; он зависит от гидродинамических условий, определяемых в основном скоростью потока и масштабом турбулентности

Конвективный перенос. Скорость конвективного переноса вещества вместе с самой средой в направлении, совпадающем с направлением, общего потока, равна (12) , где u — скорость потока жидкости, газа или пара; K — коэффициент пропорциональности.

Суммарный перенос вещества в движущейся среде, по аналогии с теплообменом, называют конвективным массообменом (конвективной диффузией). Распределение концентраций при конвективном массообмене определяется в самом общем виде дифференциальным уравнением массообмена в движущейся среде (часто в литературе это уравнение носит название дифференциального уравнения конвективной диффузии), которое для неустановившегося процесса записывается в следующем виде: (13) , где ux, uy, uz, Dx, Dy, Dz – составляющие скорости ветра и коэффициента диффузии по осям x, y, z; - отражает локальное изменение концентрации распределяемого вещества во времени.

При массообмене в неподвижной среде и конвективная составляющая в левой части уравнения равна нулю, и уравнение обращается в уравнение молекулярной диффузии: (14) , Это уравнение носит название второго закона Фика, описывающего скорость изменения концентрации за счет диффузии в каждой точке среды.

Таким образом, повторим, что молекулярная диффузия осуществляется в результате хаотического движения молекул вещества в неподвижной среде (примеры, растворение сахара в воде, проникание капель отравляющих веществ через материалы, рассеяние АХОВ в бессточных водоемах, рассеяние АХОВ в безветренную погоду). Конвективный перенос – макроскопическое движение всей среды (совместно с молекулярной диффузией), например, рассеяние АХОВ при несильном устойчивом ветре. Турбулентная диффузия – перенос вещества в пространстве в результате хаотического движения вихрей различного размера, например, рассеяние АХОВ в верхних слоях атмосферы или в приземном слое при сильном ветре.

В дифференциальном уравнении массообмена в движущейся среде, помимо концентрации, переменной является скорость потока. Поэтому данное уравнение надо рассматривать совместно с дифференциальными уравнениями гидродинамики: уравнениями движения Навье — Стокса и уравнением неразрывности потока. Однако эта система уравнений не имеет аналитического решения и для получения расчетных зависимостей по массообмену приходится прибегать к преобразованию дифференциального уравнения массообмена в движущейся среде методами теории подобия.

Рассеяние в атмосфере загрязнителей зависит от многих взаимосвязанных факторов: физических и химических свойств вещества выбросов, метеорологических условий в окружающей атмосфере, размещения источника выброса препятствий движению воздуха относительно и характера местности в направлении ветра от источника. Было предложено несколько аналитических методов для того, чтобы связать рассеяние выбросов с отдельными из упомянутых выше факторов, однако ни один из этих методов не учитывает полную их совокупность.

Возможность прогноза концентраций загрязнителей в окружающем воздухе при химических авариях основывается на математических моделях рассеяния примесей в основном от наземных одиночных источников. Однако применение рассмотренного уравнения турбулентной диффузии к реальным процессам в атмосфере затруднительно. Поэтому обычно делаются следующие дополнительные допущения: 1. Загрязнители выбрасываются из непрерывного точечного источника. 2. Процесс квазистационарен, т. е. d. C/dt=0. 3. Направление основного переноса, обусловленного ветром, совпадает с осью х. 4. Скорость ветра u предполагается постоянной в любой, точке в системе координат х, у, z. 5. Перенос загрязнителей по ветру в направлении оси х преобладает над диффузией вдоль направления ветра, т. е. , (15)

В результате уравнение диффузии принимает вид (16) , где Решение этого уравнения должно удовлетворять следующим граничным условиям: (высокая концентрация, в самом источнике). при 1. 2. при (нулевая концентрация при большом удалении от источника). 3. отсутствует). при (диффузия на поверхности 4. (скорость переноса загрязнителей в направлении ветра постоянна и равна скорости выброса Q из источника).

Однако, к сожалению, это аналитически решенное уравнение при сравнении расходится с экспериментальными данными. Поэтому для моделирования рассеяния примесей в настоящее время широко применяется статистическая модель гауссовой струи. Она представляет собой статистически «нормальное» распределение концентраций, но требует обширной информации о коэффициентах массовой диффузии в направлениях осей у и z.

Говорят, что переменная х распределена нормально, если выполняется следующее соотношение для функции плотности (17) , где: - любое действительное число; - любое действительное число больше нуля, называемое среднеквадратическим отклонением

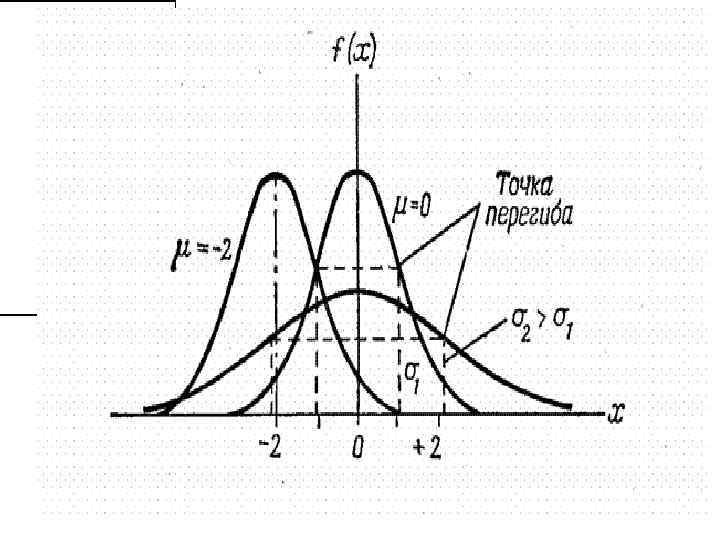
Ввиду того, что нормальное распределение концентраций соответствует двум осям у и z, то уравнение рассеяния будет иметь вид двойного гауссова распределения, которое получается простым перемножением двух гауссовых распределений по каждой из этих координатных осей (18) ,

Для точечного источника на уровне земли с использованием гауссова приближения для описания поля концентрации используется выражение , (19) где: C(x, y, z) - концентрация от точечного источника в точке с координатами х, у, z; Q - мощность источника выброса, например, кг/с; u - скорость ветра; у, z - стандартные отклонения, определяющие рассеяние примеси в направлениях у и z соответственно.

Значения у, z связаны с коэффициентами диффузии или коэффициентами массовой диффузии газа через другую подвижную среду в направлении осей y и z. Кроме этого, из физического характера диффузии следует, что стандартные отклонения по осям у и z являются функциями положения точки х в направлении ветра от источника, а также функциями устойчивости атмосферы. Для оценки их величин и определения их взаимосвязи было проведено много экспериментальных исследований в атмосфере. В результате были получены различные диаграммы для этих двух параметров.

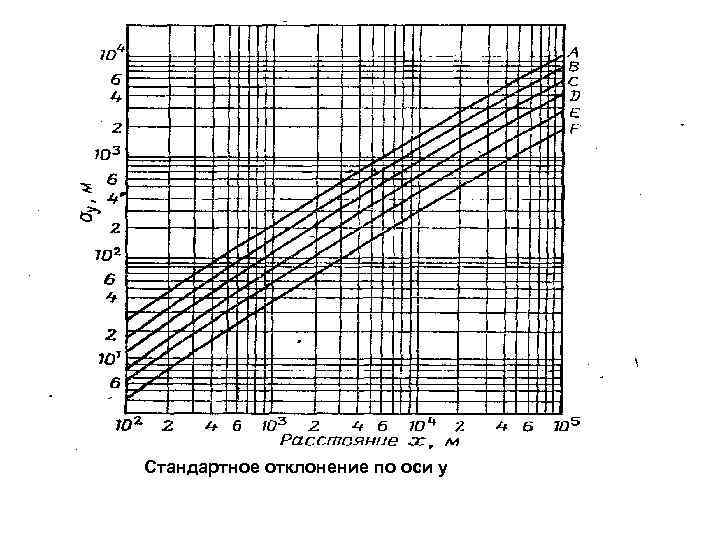Стандартное отклонение по оси у

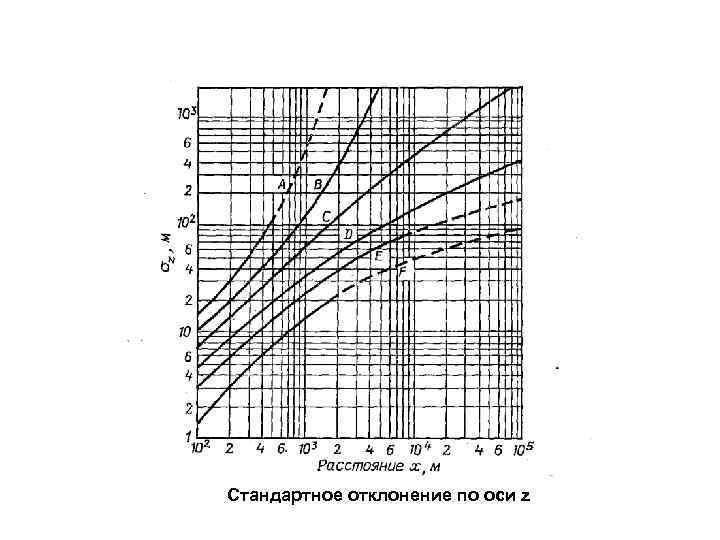Стандартное отклонение по оси z

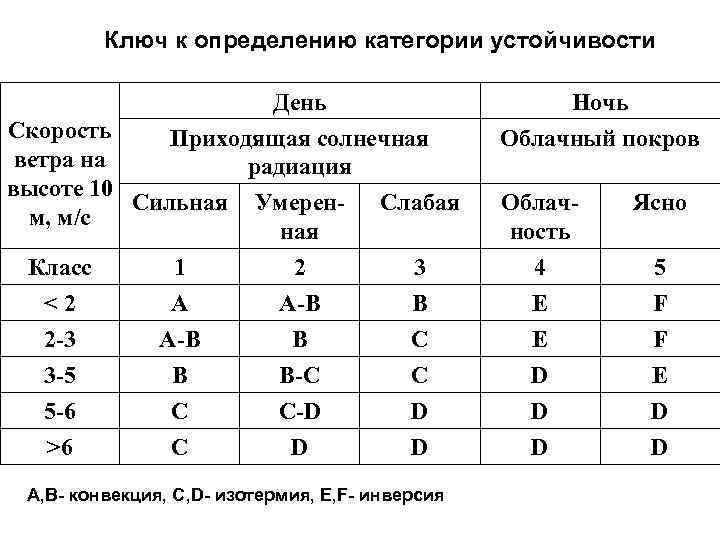Ключ к определению категории устойчивости День Скорость Приходящая солнечная ветра на радиация высоте 10 Сильная Умерен- Слабая м, м/с ная Класс < 2 2 -3 3 -5 5 -6 >6 1 А A-B B C C 2 А-В B B-C C-D D 3 В C C D D А, В- конвекция, С, D- изотермия, Е, F- инверсия Ночь Облачный покров Облачность Ясно 4 Е E D D D 5 F F E D D

Особенности модели рассеяния радиоактивных облаков при радиационных авариях

Радиационная авария - авария на радиационно опасном объекте, приводящая к выходу или выбросу радиоактивных веществ и (или) ионизирующих излучений за предусмотренные проектом для нормальной эксплуатации данного объекта границы в количествах, превышающих установленные пределы безопасности его эксплуатации (ГОСТ Р 22. 0. 05– 94).

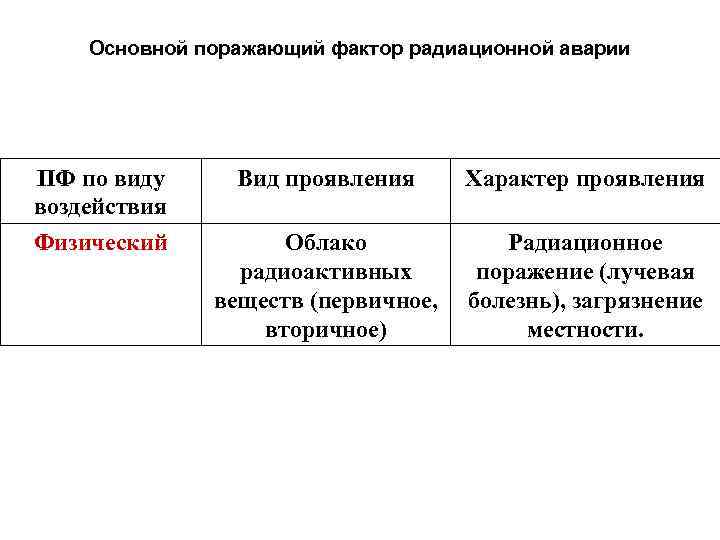Основной поражающий фактор радиационной аварии ПФ по виду воздействия Физический Вид проявления Характер проявления Облако Радиационное радиоактивных поражение (лучевая веществ (первичное, болезнь), загрязнение вторичное) местности.

Некоторые особенности модели рассеяния от точечного источника на высоте с учетом отражения

z - H

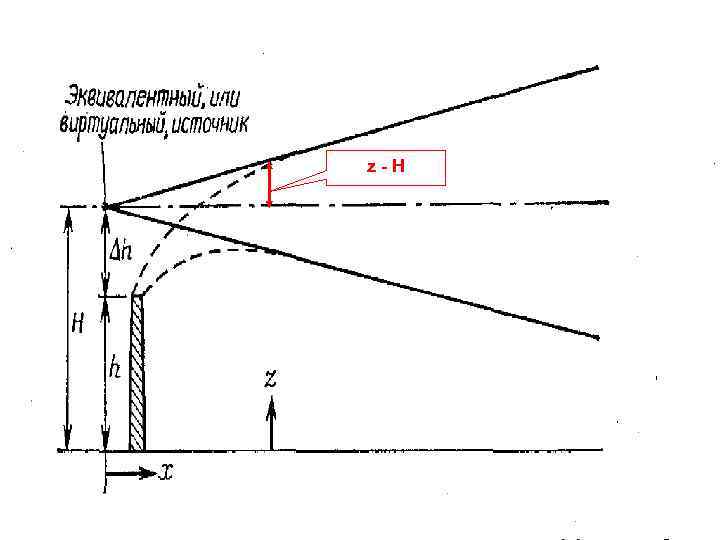
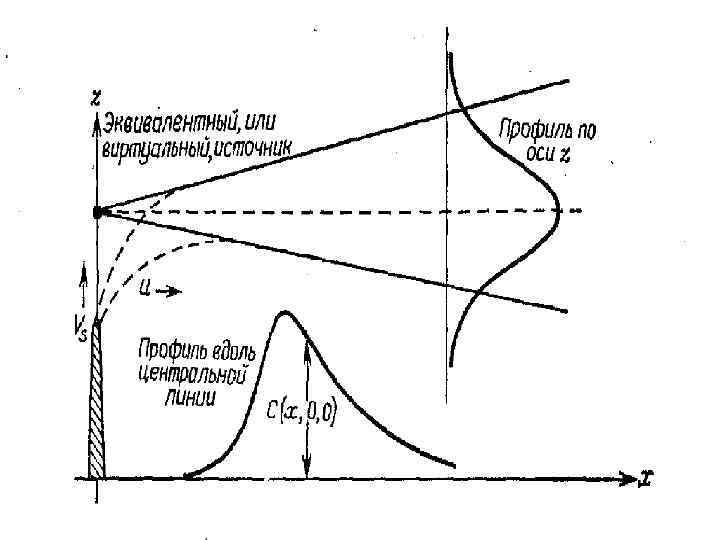
Для приподнятого точечного источника газообразного загрязнителя на высоте Н без учета отражения поле распределения концентраций может быть определено по выражению: , (20) Оговорка «без учета отражения» чрезвычайно важна. Это уравнение оказывается подходящим выражением для концентрации в направлении ветра до точки на оси х, где концентрация на уровне земли (z=0) оказывается значимой. В этом случае заметное «отражение» газообразного загрязнителя будет проявляться в форме диффузии обратно от поверхности земли в атмосферу. Такая модель предполагает, что поверхность земли не является стоком (т. е. уловителем) для загрязнителя.

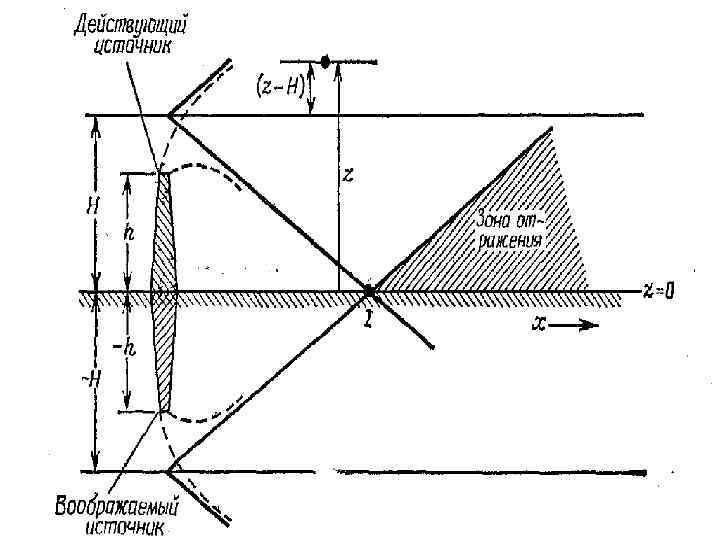
Обращаясь к предыдущему рисунку, мы увидим, что отражение на некотором расстоянии х математически эквивалентно наличию зеркального отражения источника с ординатой –Н. Затененная площадь после точки I на диаграмме показывает область атмосферы, в которой концентрация увеличивается сверх той, которая соответствует источнику с высотой Н. Это увеличение концентрации определяется математически линейной суперпозицией двух кривых гауссова типа, одной с центром на высоте Н и другой - на высоте –Н. Это эквивалентно объединению двух уравнений, подобных уравнению (20). Однако одно из них содержит член (z-H), тогда как другое – член (z+H). В итоге уравнение для концентрации для приподнятого источника с учетом отражения будет иметь вид

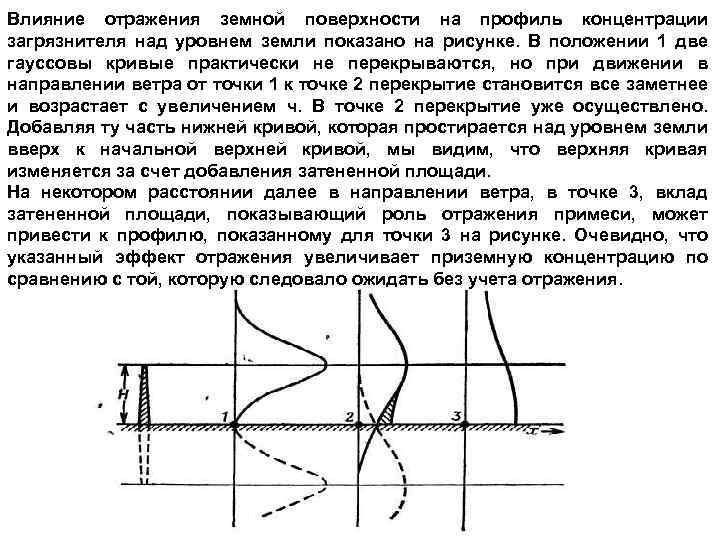Влияние отражения земной поверхности на профиль концентрации загрязнителя над уровнем земли показано на рисунке. В положении 1 две гауссовы кривые практически не перекрываются, но при движении в направлении ветра от точки 1 к точке 2 перекрытие становится все заметнее и возрастает с увеличением ч. В точке 2 перекрытие уже осуществлено. Добавляя ту часть нижней кривой, которая простирается над уровнем земли вверх к начальной верхней кривой, мы видим, что верхняя кривая изменяется за счет добавления затененной площади. На некотором расстоянии далее в направлении ветра, в точке 3, вклад затененной площади, показывающий роль отражения примеси, может привести к профилю, показанному для точки 3 на рисунке. Очевидно, что указанный эффект отражения увеличивает приземную концентрацию по сравнению с той, которую следовало ожидать без учета отражения.

3. Определение вероятности поражения людей при химических авариях Независимо от модели образования поражающих факторов дальнейшее их воздействие на население будем рассматривать в рамках единого механизма, так как оно подчиняется одним и тем же закономерностям и обусловливается сходными явлениями и процессами, к которым относятся: процесс испарения, продолжительность поражающего АХОВИД; определяющий действия облака закономерности распространения приземном слое атмосферы; поражающее воздействие на людей. примеси в

Исходными данными для математического описания сценария аварии на этой фазе служат: тип АХОВИД и характеристики его токсичности; количество АХОВИД, перешедшего в атмосферу; характер разлива поверхность; АХОВИД на метеорологические характеристики; защищенность людей. подстилающую

В качестве основных элементов математической модели третьей фазы аварии выделены следующие составляющие: поля концентраций, определяемые по первичному и вторичному облакам; времена подхода облаков зараженного воздуха к определенному рубежу и их экспозиционное токсическое воздействие на людей; поле суммарных токсоэффектов в зависимости от времени экспозиции, величины поражающей ингаляционной токсодозы (с учетом принципа суперпозий от первичного и вторичного облаков) и защищенности населения.

Для учета совместного влияния рельефа местности, населенных пунктов и лесов на распределение концентраций АХОВИД использован метод “эквивалентных расстояний”. Вместо фактически пройденного облаком расстояния х по горизонтальному направлению вводится “эквивалентное расстояние” хэкв , которое больше х, если на пути распространения были возвышенности, леса, населенные пункты , (21) где: - сумма превышений местности над горизонтальной линией, проходящей через источник; - соответственно, суммарные расстояния, пройденные облаком над лесом и населенными пунктами.

Поле концентраций является исходным моментом для определения тяжести поражения людей при авариях на ХОО. Основной оценкой при этом является доза, вызывающая определенный токсический эффект. Для характеристики токсичности АХОВИД при их воздействии на организм человека через органы дыхания чаще всего используются следующие уровни (категории) медианных значений относительной ингаляционной токсодозы (далее ингаляционной токсодозы): Lct 50 - медианное значение смертельной относительной ингаляционной токсодозы (гибель 50 %-ов пораженных); Ict 50 - медианное значение выводящей из строя относительной ингаляционной токсодозы (50 %-ов пораженных требуют госпитализации); Ect 50 - медианное значение эффективно действующей относительной ингаляционной токсодозы (50 %-ам пораженных требуется оказание первой врачебной помощи); Pct 50 - медианное значение пороговой относительной токсодозы (у 50 %-ов пораженных наблюдается нестойкий эффект от воздействия).

Однако этих характеристик недостаточно для оценки структуры потерь. Для этого необходимо знать вид зависимости “доза - эффект”. Кривые зависимости “доза - эффект” представляют собой S - образные линии. Для практического их использования абсолютную величину дозы заменяют безразмерной величиной, называемой токсоэффектом, определяемого по формуле , (22) где: T D Dэф - значение токсоэффекта; - токсодоза, полученная человеком; - значение токсодозы, вызывающий определенный эффект поражения.

Токсоэффект позволяет: связать в единый безразмерный показатель количественных характеристик поражающих факторов АХОВИД с их токсикологическими характеристиками; получить статический и динамический законы токсичности, устанавливающие связь между величиной создаваемого в точке токсоэффекта с вероятностью поражения человека в этой точке; достаточно просто рассчитать суммарный эффект при одновременном воздействии различных поражающих факторов аварии на ХОО и видов АХОВИД.

Универсальный статический закон токсичности описывается выражением , (23) где: F(T) - функция универсального статического закона токсичности; Т - величина токсоэффекта; KT - параметр, связанный с дисперсией случайного значения токсоэффекта, и на основании экспериментальных исследований может быть принят равным 1, 06; erf - интеграл ошибок (табулированная функция). F(T) можно рассматривать как зависимость между долей людей, получивших поражений не ниже заданной степени тяжести, и величиной создаваемого токсоэффекта. F(T) практически не зависит от типа АХОВИД и путей воздействия их на организм. Закон токсичности позволяет рассчитывать структуру потерь при поражении АХОВИД.

Структура пораженных по различным возрастным группам определяется по формуле T = k T , (24) i i в где: Ti - токсоэффект i-ой возрастной группы; Tв - токсоэффект для взрослой возрастной группы; ki - поправочный коэффициент для i-ой возрастной группы: Возраст, лет 20 18 14 6 1 k 1 1, 33 2 4 12, 5

При известном возрастном составе населения структура потерь оценивается с использованием средневзвешенного значения , (25) где: - средневзвешенное значение токсоэффекта; Тв - токсоэффект для взрослой возрастной группы; n - количество возрастных групп; Аi - доля i-ой возрастной группы населения в общем числе пострадавших. Условия защищенности населения учитываются путем введения в формулу (25) коэффициентов защищенности.

При определении потерь важное значение имеет правильное определение воздействующей токсодозы, зависящей от концентрации в наблюдаемой точке и времени ее воздействия (экспозиции). Для постоянно действующего точечного источника время экспозиции на удалении от источника заражения определяется длительностью действия источника заражения, временем подхода облака зараженного воздуха и временем сохранения метеорологической устойчивости атмосферы. В этом случае в зависимости от их длительности будет изменяться время экспозиции.

С достаточной степенью точности при планировании защитных мероприятий и проведения проектных работ экспозиционную токсодозу на различном удалении от источника нами предложено определять из условия , (25) где: D - экспозиционная ингаляционная токсодоза; С - осредненная концентрация АХОВИД в точке за время подхода облака и его воздействия, определяемая по (26); метео - время сохранения метеорологической устойчивости атмосферы; подхода - время подхода облака зараженного воздуха к рассматриваемой точке; исп - длительность испарения АХОВИД (время действия постоянного точечного источника заражения).

При расчетах концентраций (токсодоз) примеси можно принимать, что категория устойчивости атмосферы сохраняется примерно неизменной с момента начала аварийного выброса: утром и вечером - не более 3 часов; днем и ночью в весеннее и осеннее время, а также днем зимой и ночью - не более 6 часов; днем в летнее время и ночью в зимнее время - не более 9 часов. За среднюю величину устойчивости атмосферы принято значение, равное 4 часам.

Осредненная концентрация за время где: С( ) - осредненная концентрация АХОВИД в точке за время подхода облака и его воздействия; Сст( ст) - концентрация АХОВИД за стандартное время осреднения.

Для мгновенного объемного или точечного источника токсодоза определяется условием , (27) где: Cср(х) - средняя концентрация в первичном облаке на расстоянии х от источника химического заражения; u - скорость ветра; d - диаметр первичного облака на расстоянии х от источника заражения (граница облака определяется из выражения (28)). , (28) где: Сцентр - концентрация в центре облака.

Учет совместного действия первичного и вторичного облаков или мгновенных и постоянно действующих источников производится на основе принципа суперпозиций путем суммирования токсоэффектов в данной точке пространства.

Время (t) подхода облака АХОВИД к заданному рубежу определяется по формуле , (29) где: х - расстояние от источника заражения до заданного рубежа; uпер - скорость переноса фронта облака зараженного воздуха.

Общая продолжительность поражающего действия ( пораж) вторичного облака АХОВИД (время полного испарения), определяется по формуле , (30) где: Qрозлив - количество АХОВИД, подстилающую поверхность; разлившегося на И - скорость испарения (мощность источника вторичного заражения).