 Лекция 2 -14. Пример. l Возьмем 1 -е и 3 -е уравнения.
Лекция 2 -14. Пример. l Возьмем 1 -е и 3 -е уравнения.
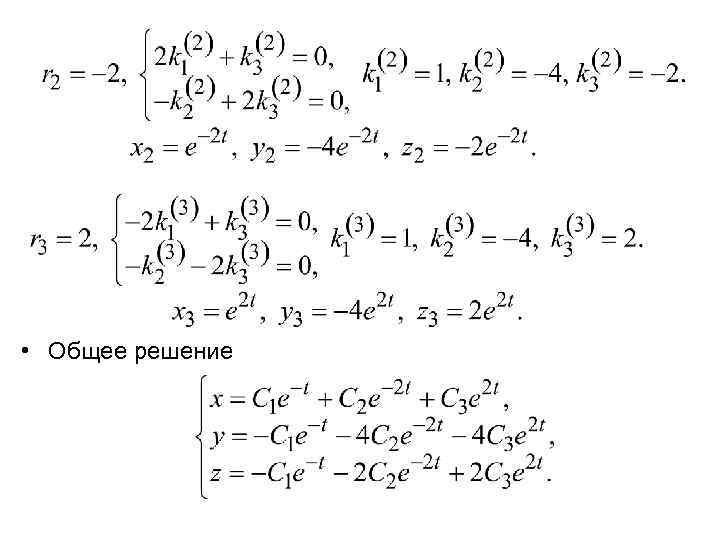 • Общее решение
• Общее решение
 l Если среди простых корней характеристического уравнения есть комплексно сопряженные, то решение будет в виде комплексных функций действительной переменной. Чтобы перейти к действительной форме используют следующее: если являются решением, то тоже решения. и
l Если среди простых корней характеристического уравнения есть комплексно сопряженные, то решение будет в виде комплексных функций действительной переменной. Чтобы перейти к действительной форме используют следующее: если являются решением, то тоже решения. и
 Пример. приведет к тем же решениям.
Пример. приведет к тем же решениям.
 l Подбор частного решения для системы неоднородных уравнений можно производить сведя систему к одному уравнению высшего порядка и используя методы, изложенные ранее.
l Подбор частного решения для системы неоднородных уравнений можно производить сведя систему к одному уравнению высшего порядка и используя методы, изложенные ранее.
 12. 4. 4. Случай кратных корней характеристического уравнения. l Для кратных корней решение усложняется. Если для одного уравнения можно сразу написать структуру общего решения, то здесь иначе. Покажем на примерах.
12. 4. 4. Случай кратных корней характеристического уравнения. l Для кратных корней решение усложняется. Если для одного уравнения можно сразу написать структуру общего решения, то здесь иначе. Покажем на примерах.
 Пример 1. l l Для кратного корня система уравнений сводится к одному уравнению Произвольно можно задать две величины Тогда т. е.
Пример 1. l l Для кратного корня система уравнений сводится к одному уравнению Произвольно можно задать две величины Тогда т. е.
 l Получили фундаментальную систему решений, т. к. l Общее решение
l Получили фундаментальную систему решений, т. к. l Общее решение
 Пример 2. l l Третье решение таким способом получить не удастся.
Пример 2. l l Третье решение таким способом получить не удастся.
 Будем искать решение в виде где определяются методом неопределенных коэффициентов. Продифференцируем и подставим в систему дифференциальных уравнений. После сокращения на получим • Приравнивая коэффициенты при степенях получим • Полагая • имеем Итак
Будем искать решение в виде где определяются методом неопределенных коэффициентов. Продифференцируем и подставим в систему дифференциальных уравнений. После сокращения на получим • Приравнивая коэффициенты при степенях получим • Полагая • имеем Итак
 • Решение с индексом 2 получается, если • Если положить получим третье решение • Три решения образуют фундаментальную систему решений.
• Решение с индексом 2 получается, если • Если положить получим третье решение • Три решения образуют фундаментальную систему решений.
 Правило. l Если характеристическое уравнение системы дифференциальных уравнений имеет корень кратности , то ему отвечает решение, зависящее от произвольных постоянных l где выше - многочлены степени не
Правило. l Если характеристическое уравнение системы дифференциальных уравнений имеет корень кратности , то ему отвечает решение, зависящее от произвольных постоянных l где выше - многочлены степени не
 12. 4. 5. Матричная форма записи системы дифференциальных уравнений. l l l Частные решения Общее решение
12. 4. 5. Матричная форма записи системы дифференциальных уравнений. l l l Частные решения Общее решение
 Определение. l Система векторных функций называется линейно независимой, если l Это выполняется, если определитель Вронского
Определение. l Система векторных функций называется линейно независимой, если l Это выполняется, если определитель Вронского
 Частное решение отыскиваем в виде • Тогда Подставим в систему • дифференциальных уравнений где - собственное число матрицы - собственный вектор матрицы • Характеристическое уравнение
Частное решение отыскиваем в виде • Тогда Подставим в систему • дифференциальных уравнений где - собственное число матрицы - собственный вектор матрицы • Характеристическое уравнение