Лекция 2 1 Уравнение состояния идеального газа

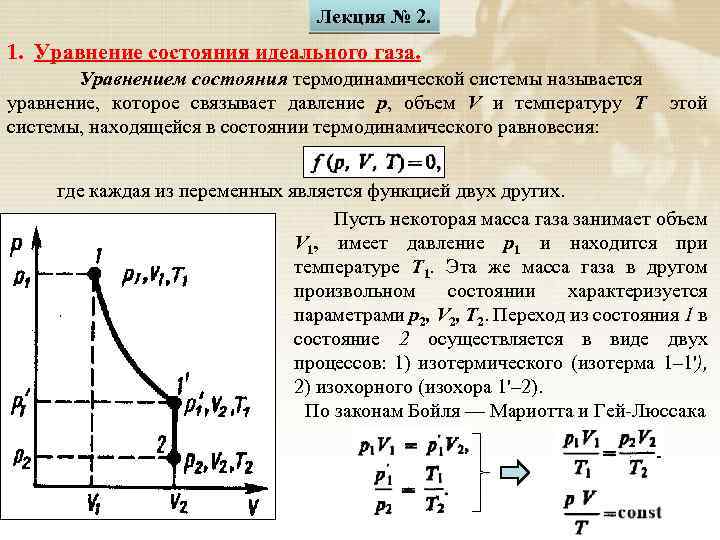Лекция № 2. 1. Уравнение состояния идеального газа. Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p, объем V и температуру T системы, находящейся в состоянии термодинамического равновесия: этой где каждая из переменных является функцией двух других. Пусть некоторая масса газа занимает объем V 1, имеет давление р1 и находится при температуре T 1. Эта же масса газа в другом произвольном состоянии характеризуется параметрами р2, V 2, T 2. Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов: 1) изотермического (изотерма 1– 1'), 2) изохорного (изохора 1'– 2). По законам Бойля — Мариотта и Гей-Люссака

Уравнение Менделеева-Клапейрона – уравнение состояния для массы m идеального газа где R=8, 31 Дж/(моль К) – универсальная газовая постоянная; =m/M — количество вещества. Если использовать постоянную Больцмана: Тогда где NA/Vm = n — концентрация молекул (число молекул в единице объема). Таким образом: 1) давление идеального газа при данной температуре прямо пропорциально концентрации его молекул; 2) при одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул.

2. Основное уравнение молекулярно-кинетической теории идеальных газов. Пусть в сосуде объемом V находится идеальный газ массой m, состоящий из N молекул массой m 0 движущихся с одинаковыми скоростями v. Концентрация молекул по определению n=N/V. Давление, оказываемое газом на стенку сосуда Если газ в объеме V содержит N молекул, движущихся со скоростями v 1, v 2, . . . , v. N, то целесообразно рассматривать среднюю квадратичную скорость, характеризующую всю совокупность молекул газа: Основное уравнение молекулярно-кинетической теории идеальных газов: Учитывая, что n =N / V, где Е — суммар. кинетическая энергия поступательного движения всех молекул.

3. Средняя квадратичная скорость молекул идеального газа: где M=m 0 NА, где т0 — масса одной молекулы, a NА — постоянная Авогадро k=R/NА — постоянная Больцмана. Средняя кинетическая энергия поступательного движения одной молекулы идеального газа Из этого уравнения следует, что при Т=0 < 0>=0, т. е. при 0 К прекращается поступательное движение молекул газа, а следовательно, его давление равно нулю. Молекулярно-кинетическое толкование температуры: термодинамическая температура – есть мера средней кинетической энергии поступательного движения молекул газа.

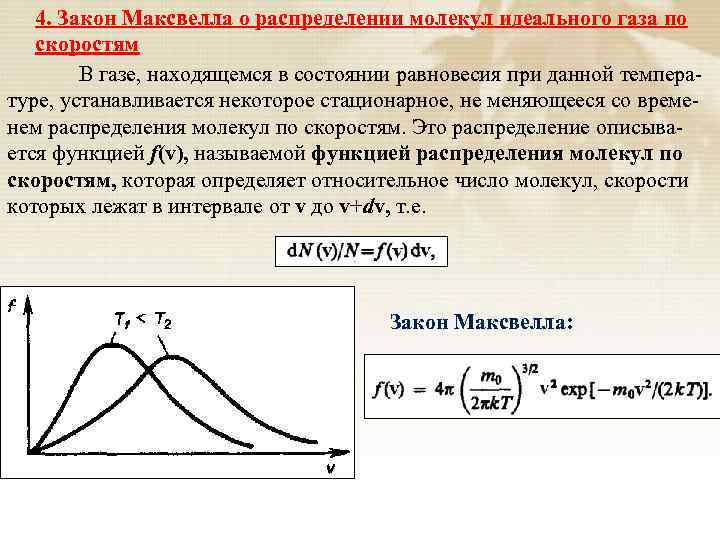4. Закон Максвелла о распределении молекул идеального газа по скоростям В газе, находящемся в состоянии равновесия при данной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределения молекул по скоростям. Это распределение описывается функцией f(v), называемой функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от v до v+dv, т. е. Закон Максвелла:

5. Наиболее вероятная скорость молекул идеального газа. Скорость, при которой функция распределения молекул идеального газа по скоростям максимальна, называется наиболее вероятной скоростью vв Приравняв С повышением температуры vв растет. 6. Средняя скорость молекулы газа (средняя арифметическая скорость Подставляя сюда f(v) и интегрируя, получаем 7. Скорости, характеризующие состояние газа.