МОР_Лекция2.ppt
- Количество слайдов: 16

Лекция 2 1. Потоки событий. Ординарность, отсутствие последействия, стационарность. 2. Независимые потоки. Интенсивность потока. Сложение потоков 3. Простейший поток событий. 4. Структура простейшего потока событий. 5. Случайный процесс с непрерывным временем и дискретными состояниями. Граф состояний. Вероятности состояний 6. Уравнения Колмогорова, мнемоническое правило 1. Потоки событий. Ординарность, отсутствие последействия, стационарность. Потоком событий называется последовательность однородных событий, появляющихся одно за другим в случайные моменты времени. Рассмотрим примеры. - Поток вызовов на АТС. - Поток автомашин, подъезжающих на АЗС. - Поток заявок на ремонт, поступающих в ремонтную мастерскую. - Поток окончаний ремонта. - Поток поездов, прибывающих на вокзал. -Поток оценок « 2» на экзамене по информатике.

Следует отметить, что события потока не обладают вероятностью. Можно рассматривать только вероятности некоторых событий, являющихся производными от событий потока. Пример: С= {в течении времени от t 1 до t 2 придет хотя бы один вызов на АТС}. Потоки событий различаются между собой по их внутренней структуре: по законам распределения интервалов времени между событиями, их взаимной зависимости или независимости Поток событий, в котором интервалы времени между событиями одинаковы и равны неслучайной величине, называется регулярным. Примеры регулярных потоков: - Поток деталей на сборочном конвейере. - Поток изменений минутной цифры на электронных часах.

Рассмотрим основные свойства потоков. 1. Ординарность. Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами по 2, 3 и т. д. Ординарность потока означает, что вероятность попадания на малый участок [t 1, t 2] двух или более событий пренебрежимо мала по сравнению с вероятностью попадания на него ровно одного события. Рассмотрим примеры: - Поток деталей, поступающих на конвейер для сборки; - Поток машин, прибывающих на станцию техобслуживания; - Поток отказов сложных систем; - Поток автомашин на центральной улице города. 2. Отсутствие последействия (поток без памяти) Пусть - число событий потока, попадающих на промежуток Поток событий называется потоком без последействия, если для любых непересекающихся промежутков времени [t 1, t 1+τ1] и [t 2 , t 2+τ2 ] случайные величины X 1 и X 2 независимы. Это означает, что вероятность попадания какого-либо числа событий на участок [t 2, t 2+τ2 ] не зависит от того, сколько событий попало на участок [t 1 , t 1+τ1 ].

Примеры. 1. Поток требований по выплатам, поступающих в страховую компанию 2. Поток оценок « 4» на экзамене по информатике 3. Стационарность. Поток событий называется стационарным, если все его вероятностные характеристики не зависят от времени. Это означает, что случайные величины X 1 и X 2 имеют одинаковые законы распределения. Вероятность попадания определенного числа событий на участок длины t не зависит от того, где именно на оси времени этот участок расположен

2. Независимые потоки. Интенсивность потока. Сложение потоков Рассмотрим потоки П 1 и П 2 Потоки П 1 и П 2 называются независимыми, если для любых t 1 и t 2 случайные величины X 1 и X 2 являются независимыми. Интенсивность потока (плотность потока). Пусть X - число событий потока, попадающих на промежуток времени [t, t+Δt], M(X(t, Δt)) - математическое ожидание этой случайной величины. Величина называется интенсивностью потока в момент времени t Интенсивность потока – среднее число событий потока, приходящееся на единицу времени (в общем случае зависит от времени).

Рассмотрим ординарный поток. Распределение случайной величины имеет вид В силу ординарности потока при В связи с этим , 1. Если и Следовательно, - мало, то , откуда 2. Среднее число событий, попадающих на промежуток времени определяется по формуле получаем

Сложение потоков

3. Простейший поток событий Поток событий называется простейшим, если он обладает тремя свойствами: а) ординарностью; б)отсутствием последействия; в)стационарностью (такой поток называют еще стационарным пуассоновским потоком. ) В теории потоков доказана теорема (аналог центральной предельной теоремы в теории вероятностей): Пусть есть n стационарных независимых и ординарных потоков, интенсивности которых . Сложение этих потоков при большом дает простейший поток, интенсивность которого определяется по формуле.

4. Структура простейшего потока Теорема 1. Пусть - число событий потока, попадающих на промежуток Случайная величина , т. е. . имеет распределение Пуассона с параметром справедлива формула где Д. Отрезок разобьем на мелких частей длиной - число событий потока, попадающих на участок

. В силу ординарности и стационарности потока В силу отсутствия последействия Тогда - независимые случайные величины и имеет биномиальное распределение с параметрами и Таким образом, и при В этом случае биномиальное распределение приближается к распределению Пуассона или

Пусть Теорема 2. - интервал времени между двумя соседними событиями потока Случайная величина имеет показательное распределение с параметром Д. По определению Если Рассмотрим события , то

Тогда Таким образом или. , 5. Случайный процесс с непрерывным временем и дискретными состояниями. Граф состояний. Вероятности состояний Рассмотрим пример. Компьютерная сеть состоит из двух компьютеров – К 1 и К 2. Если компьютер выходит из строя, то он мгновенно начинает ремонтироваться. По окончании ремонта также мгновенно включается в работу. Компьютеры работают независимо друг от друга. Время ремонта, моменты отказов – случайные величины. Потоки отказов и потоки восстановлений компьютеров предполагаются простейшими.
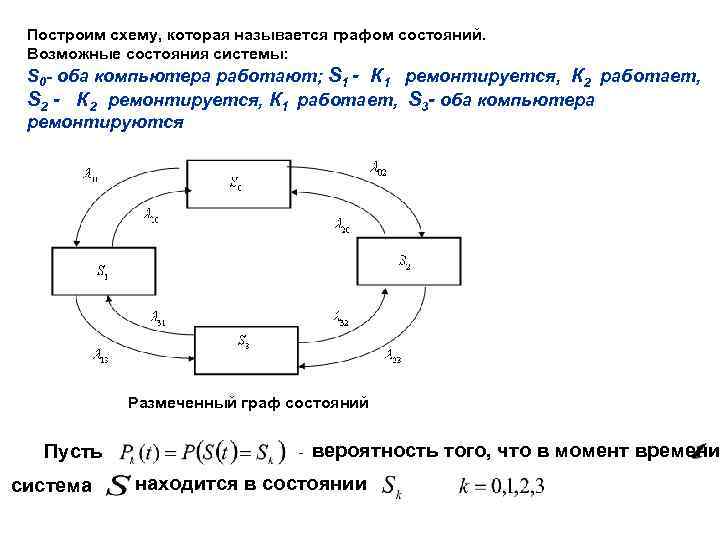
Построим схему, которая называется графом состояний. Возможные состояния системы: S 0 - оба компьютера работают; S 1 - К 1 ремонтируется, К 2 работает, S 2 - К 2 ремонтируется, К 1 работает, S 3 - оба компьютера ремонтируются Размеченный граф состояний Пусть система - вероятность того, что в момент времени находится в состоянии

6. Уравнения Колмогорова, мнемоническое правило Рассмотрим события: Найдем эту вероятность. Здесь мало, в силу ординарности потока может произойти только одно событие потока. В каком состоянии система могла находиться в момент времени Очевидно, Формула полной вероятности: ?


Мнемоническое правило (схема для упрощения запоминания) Введем понятие потока вероятности. Величина систему из состояния называется потоком вероятности. Он выводит и переводит в состояние Получаем систему дифференциальных уравнений
МОР_Лекция2.ppt