Скачать презентацию Лекция 2 1 Лекция 2 Системы счисления Скачать презентацию Лекция 2 1 Лекция 2 Системы счисления

Lektsiya_2-2015_KO.ppt

  • Количество слайдов: 46

Лекция 2 1 Лекция 2 1

Лекция 2 Системы счисления, выбор системы счисления для использования в компьютерных системах Основные методы Лекция 2 Системы счисления, выбор системы счисления для использования в компьютерных системах Основные методы перевода чисел в позиционных системах 2

Лекция 2 1. Системы счисления, выбор системы счисления для использования в компьютерных системах 3 Лекция 2 1. Системы счисления, выбор системы счисления для использования в компьютерных системах 3

Системы счисления, выбор системы счисления для использования в компьютерных системах Основные определения: Система Системы счисления, выбор системы счисления для использования в компьютерных системах Основные определения: Система счисления - строго определенная совокупность приемов и правил для наименования и отображения чисел с помощью набора символов, которые называются цифрами. Цифры - знаки, используемые при записи чисел. Числа и цифры различаются между собой так же, как различаются между собой слова и буквы. Основные виды систем счисления: - Унарная (числа отображаются засечками, черточками, палочками и т. д. ); - Непозиционная (от положения цифры в записи не зависит величина, которую она означает); - Позиционная (величина, обозначаемая цифрой в записи числа, зависит от ее позиции в этой записи) Позиция - место цифры в числе. 4

Системы счисления, выбор системы счисления для использования в компьютерных системах Примеры непозиционных систем Системы счисления, выбор системы счисления для использования в компьютерных системах Примеры непозиционных систем счисления: l l l древнеегипетская; римская (I = 1; V = 5, X = 10; L = 50; D = 500; M = 1000); алфавитная. Примеры позиционных систем счисления: l l l вавилонская (шестидесятеричная); пятеричная; двенадцатеричная; двадцатеричная; с ступенчатой весом разрядов (десятичная, шестнадцатеричная, восьмеричная, троичная, двоичная). 5

УНАРНЫЕ СИСТЕМЫ В унарных системах счисления число образуется путем повторения одного знака, символизирующего единицу. УНАРНЫЕ СИСТЕМЫ В унарных системах счисления число образуется путем повторения одного знака, символизирующего единицу. Способ записи: зарубки, чёрточки, палочки 6

Археологами найдены такие Археологами найдены такие "записи" при раскопках культурных слоев, относящихся к периоду палеолита (10 - 11 тыс. лет до н. э. ) Этот способ записи чисел называют единичной ("палочной”, “унарной”) системой счисления Единичная запись для таких чисел была громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа. 7

Непозиционные системы В таких системах счисления от положения знака в записи числа не зависит Непозиционные системы В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает. XXIV Римская Египетская j Древнегреческая Славянская 8

Египетская нумерация 1 10000 10 100000 10000000 Была создана 5000 лет тому назад 9 Египетская нумерация 1 10000 10 100000 10000000 Была создана 5000 лет тому назад 9

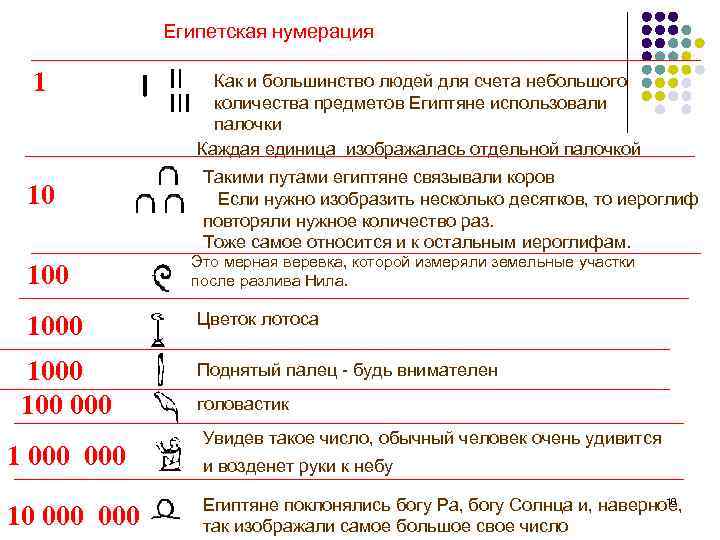Египетская нумерация 1 10 1000 100 000 10 000 Как и большинство людей для Египетская нумерация 1 10 1000 100 000 10 000 Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки Каждая единица изображалась отдельной палочкой Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам. Это мерная веревка, которой измеряли земельные участки после разлива Нила. Цветок лотоса Поднятый палец - будь внимателен головастик Увидев такое число, обычный человек очень удивится и возденет руки к небу 10 Египтяне поклонялись богу Ра, богу Солнца и, наверное, так изображали самое большое свое число

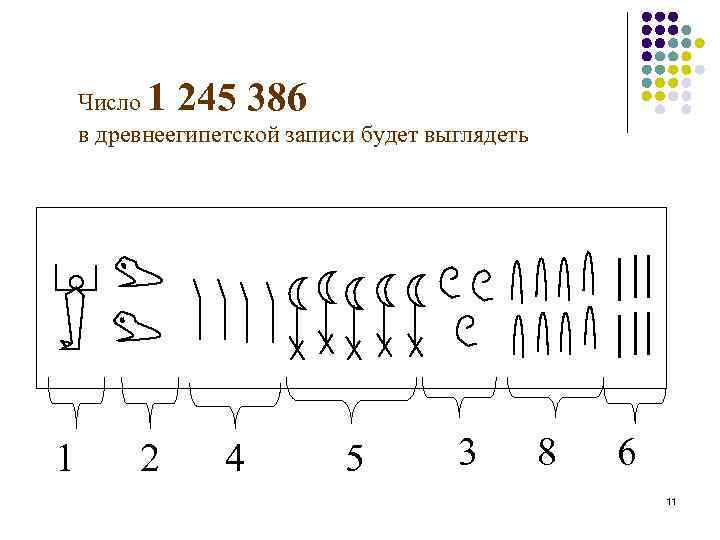1 245 386 Число в древнеегипетской записи будет выглядеть 1 2 4 5 3 1 245 386 Число в древнеегипетской записи будет выглядеть 1 2 4 5 3 8 6 11

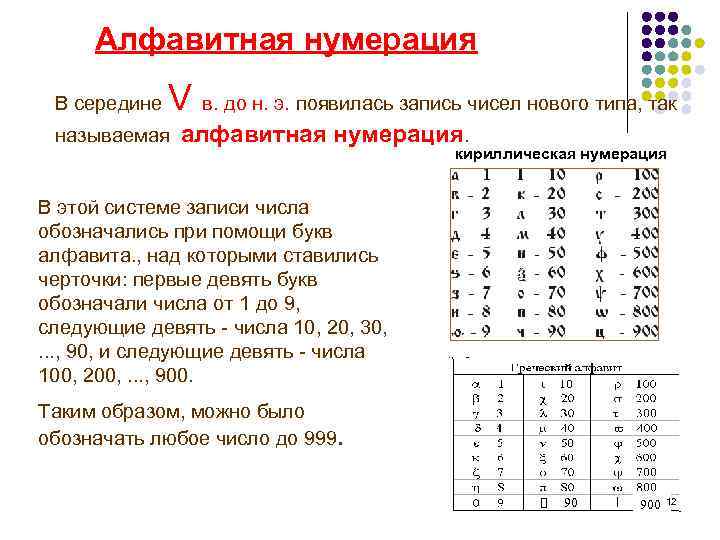Алфавитная нумерация В середине V в. до н. э. появилась запись чисел нового типа, Алфавитная нумерация В середине V в. до н. э. появилась запись чисел нового типа, так называемая алфавитная нумерация. кириллическая нумерация В этой системе записи числа обозначались при помощи букв алфавита. , над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, . . . , 90, и следующие девять - числа 100, 200, . . . , 900. Таким образом, можно было обозначать любое число до 999. 90 900 12

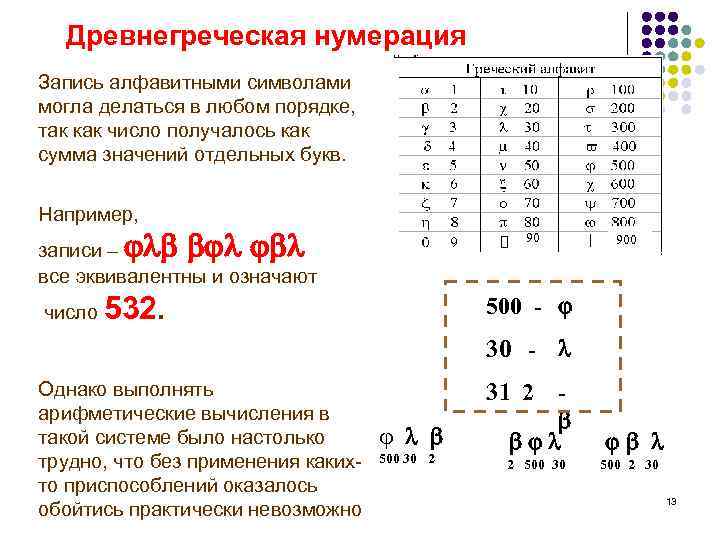Древнегреческая нумерация Запись алфавитными символами могла делаться в любом порядке, так как число получалось Древнегреческая нумерация Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв. Например, 90 записи – все эквивалентны и означают число 900 500 - 532. 30 - Однако выполнять арифметические вычисления в такой системе было настолько трудно, что без применения какихто приспособлений оказалось обойтись практически невозможно j 500 30 2 31 2 2 500 30 500 2 30 13

Славянская кириллическая нумерация 14 Славянская кириллическая нумерация 14

Чтобы различать буквы и цифры, над числами ставился особый значок — титло ( ~ Чтобы различать буквы и цифры, над числами ставился особый значок — титло ( ~ ). Так можно было записывать числа до 999. Для больших чисел использовался знак тысяч , который ставился впереди символа, обозначавшего число До XVII века эта форма записи чисел была официальной на территории России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию. 15

Римская нумерация Это нумерация, известная нам и в настоящее время. С нею мы достаточно Римская нумерация Это нумерация, известная нам и в настоящее время. С нею мы достаточно часто сталкиваемся в повседневной жизни. Это номера глав в книгах, указание века, числа на циферблате часов, и т. д. Возникла эта нумерация в древнем Риме. В ней имеются узловые числа: один, пять и т. д. Остальные числа получались путем прибавления или вычитания одних узловых чисел из других Например, четыре записывается как IV, т. е. пять минус один, восемь — VIII (пять плюс три), сорок—XL (пятьдесят минус десять), девяносто шесть—XCVI (сто минус 16 десять плюс пять и плюс еще один) и т. д.

Позиционные системы счисления, в которых вклад каждого знака в величину числа зависит от его Позиционные системы счисления, в которых вклад каждого знака в величину числа зависит от его положения (позиции) в последовательности знаков, изображающей число • Вавилонская Название системы зависит от количества используемых в ней знаков. • Десятичная • Двоичная • Восьмеричная • Двенадцатеричная • и др. 17

Вавилонская система счисления 2500 -2000 лет до н. э. 18 Вавилонская система счисления 2500 -2000 лет до н. э. 18

Десятичная система счисления Цифры 1234567890 возникли в Индии около 400 г. н. э. Арабы Десятичная система счисления Цифры 1234567890 возникли в Индии около 400 г. н. э. Арабы стали пользоваться подобной нумерацией около 800 г. н. э. Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе 19

Из арабского языка заимствовано и слово Из арабского языка заимствовано и слово "цифра" (по-арабски "сыфр"), означающее буквально "пустое место" Это слово применялось для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин "нуль" (nullum - ничто). Форма индийских цифр претерпевала многообразные изменения. Та форма, которой мы сейчас пользуемся установилась в XVI веке. По мнению марроканского историка Абделькари Боунжира арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры 20

В древней Индии и Китае существовали системы записи, построенные на МУЛЬТИПЛИКАТИВНОМ ПРИНЦИПЕ. В таких В древней Индии и Китае существовали системы записи, построенные на МУЛЬТИПЛИКАТИВНОМ ПРИНЦИПЕ. В таких системах для записи одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда. Если десятки обозначить символом Д, а сотни - С, то число 325 будет выглядеть так : 3 С 2 Д 5. Между II и VI вв. н. э. Индийцы познакомились с греческой астрономией. Индийцы и соединили греческие принципы нумерации со своей десятичной мультипликативной системой. 21

ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Эта система является позиционной потому, что величина, обозначаемая цифрой в записи ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ Эта система является позиционной потому, что величина, обозначаемая цифрой в записи числа, зависит от её позиции. Например: 333 – три сотни, три десятка и три единицы. 333 = 3 * 100 + 3 * 10 + 3 Всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки: 26, 38=2*101 + 6*100 +3*10 -1 + 8*10 -2 Число 10 является основанием десятичной системы счисления. 22

Официальное рождение двоичной арифметики связанно с именем Г. В. Лейбница, опубликовавшего в 1703 г. Официальное рождение двоичной арифметики связанно с именем Г. В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами. Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры. Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов. 23

ВОСЬМЕРИЧНАЯ система счисления Всякое восьмеричное число можно представить как сумму произведений составляющих его цифр ВОСЬМЕРИЧНАЯ система счисления Всякое восьмеричное число можно представить как сумму произведений составляющих его цифр на соответствующие степени восьмёрки: 7764, 18=7*83 + 7*82 +6*81 + 4*80 + 1*8 -1=4084, 12510 24

Двенадцатеричная система счисления системы равно двенадцати. Используются десять цифр от 0 до 9 и Двенадцатеричная система счисления системы равно двенадцати. Используются десять цифр от 0 до 9 и две латинские буквы А и В. Основание Применение: l l l Считали фаланги пальцев Для счета использовали большой палец Число 12 – дюжина 25

l l В сутках две дюжины часов Час делится на пять дюжин минут Столовые l l В сутках две дюжины часов Час делится на пять дюжин минут Столовые сервизы на 6 или 12 персон Набор карандашей или фломастеров из 6 или 12 цветов. 26

Шестнадцатеричная система счисления Всякое шестнадцатеричное число можно представить как сумму произведений составляющих его знаков Шестнадцатеричная система счисления Всякое шестнадцатеричное число можно представить как сумму произведений составляющих его знаков на соответствующие степени числа шестнадцать: 3 AF, 816=3*162 + 10*161 +15*160 + 8*16 -1 =943, 510 27

Системы счисления, используемые в компьютере Двоичная 0, 1 Двоичная система счисления является основной системой Системы счисления, используемые в компьютере Двоичная 0, 1 Двоичная система счисления является основной системой представления информации в памяти компьютера. Восьмеричная 0, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 28

Двоичная система счисления Из всех систем счисления особенно проста и поэтому интересна для технической Двоичная система счисления Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления. Алфавит двоичной системы счисления состоит из 0 и 1 Основанием, служит цифра 2 Достоинства 2 с/с: Недостатки 2 с/с: 1. Простота кодирования; 1. Много места занимает запись числа; 2. Простота арифметических действий; 3. Простота записи, хранения и передачи техническими средствами. 2. Трудоемкость перевода в 10 с/с и наоборот. 29

Восьмеричная система счисления Шестнадцатеричная система счисления Алфавит: 0, 1, 2, 3, 4, 5, 6, Восьмеричная система счисления Шестнадцатеричная система счисления Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 810 =108 Основанием является цифра 8 Например: 2768 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F 1610=1016 Основанием является цифра 16 Например: 26 A 716 Применяется для целей коммуникации человека с ЭВМ. 30

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления? Двоичная система, удобная для Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления? Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи. Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Для программистов удобнее работать с более компактной записью. Такими системами и являются 8 -аяи 16 -ая 1000001 - двоичная 1000001 2 0 0 восьмеричная 1 4 0 1 шестнадцатеричная 31

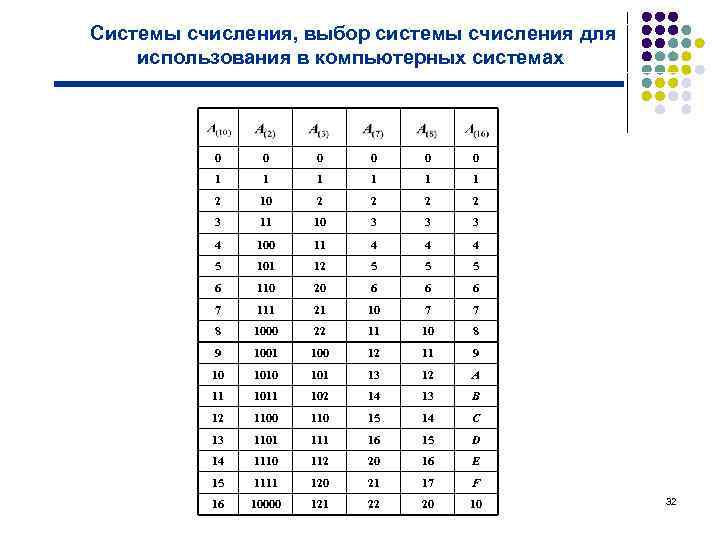Системы счисления, выбор системы счисления для использования в компьютерных системах 0 0 0 Системы счисления, выбор системы счисления для использования в компьютерных системах 0 0 0 1 1 1 2 10 2 2 3 11 10 3 3 3 4 100 11 4 4 4 5 101 12 5 5 5 6 110 20 6 6 6 7 111 21 10 7 7 8 1000 22 11 10 8 9 1001 100 12 11 9 10 101 13 12 А 11 102 14 13 B 12 1100 110 15 14 С 13 1101 111 16 15 D 14 1110 112 20 16 E 15 1111 120 21 17 F 16 10000 121 22 20 10 32

Системы счисления, выбор системы счисления для использования в компьютерных системах 33 Системы счисления, выбор системы счисления для использования в компьютерных системах 33

Формула разложения числа по степеням основания Рассмотрим, для примера, десятичное число 3745. Его можно Формула разложения числа по степеням основания Рассмотрим, для примера, десятичное число 3745. Его можно записать несколькими способами, не изменяя его количества. А 10= 3745 А 10= 3000 + 700 + 40 + 5 А 10= 3 x 1000 + 7 x 100 + 4 x 10 + 5 А 10= 3 x 103 + 7 x 102 + 4 x 101 + 5 x 100 (любое число в степени 0 равно 1) Последнюю запись называют разложением по степеням основания. 34

Ар= а nрn+…+а 1 р1+а 0 p 0 Формула разложения по степеням основания показывает, Ар= а nрn+…+а 1 р1+а 0 p 0 Формула разложения по степеням основания показывает, что число можно представить в виде суммы цифр, которые в свою очередь, равны произведению цифры на основание в степени, равной номеру разряда. При разложении целых чисел нумерация разрядов идет справа налево, начиная с « 0» . 35

Системы счисления, выбор системы счисления для использования в компьютерных системах где: – число Системы счисления, выбор системы счисления для использования в компьютерных системах где: – число в системе счисления с основанием p; - - цифры числа; - n - количество разрядов (позиций) в целой части числа; - m - количество разрядов (позиций) в дробной части числа; - k - индекс степени. Пример: 36

Лекция 2 2 Основные методы перевода чисел в позиционных системах 37 Лекция 2 2 Основные методы перевода чисел в позиционных системах 37

Основные методы перевода чисел в позиционных системах Основные методы перевода чисел: l l метод Основные методы перевода чисел в позиционных системах Основные методы перевода чисел: l l метод перевода чисел с основанием, кратным 2 n; метод замещения; метод деления (умножения) на основу; , метод вычитания степеней. 38

Основные методы перевода чисел в позиционных системах 1 МЕТОД ПЕРЕВОДА ЧИСЕЛ С ОСНОВАНИЕМ, КРАТНЫМ Основные методы перевода чисел в позиционных системах 1 МЕТОД ПЕРЕВОДА ЧИСЕЛ С ОСНОВАНИЕМ, КРАТНЫМ 2 n Для того, чтобы целое двоичное число записать в системе счисления с основанием 2 n , необходимо данное двоичное число разбить справа налево на группы по n цифр в каждой. Если при этом в последний левой группе окажутся меньше n разрядов, то необходимо дополнить ее нулями до нужного числа разрядов. Затем следует рассмотреть каждую группу как n-разрядное двоичное число и заменить ее соответствующей цифрой в системе 2 n. Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатеричную системы аналогичное разбиение на двоичные триады или тетрады производится от запятой вправо (с дополнением недостающих последних цифр нулями). 39

Основные методы перевода чисел в позиционных системах 2 МЕТОД ЗАМЕЩЕНИЯ Чаще всего используется для Основные методы перевода чисел в позиционных системах 2 МЕТОД ЗАМЕЩЕНИЯ Чаще всего используется для перевода чисел из недесятичных системы счисления в десятичную. Приклади: 40

Основные методы перевода чисел в позиционных системах 3 а метод деления (умножения) на основу Основные методы перевода чисел в позиционных системах 3 а метод деления (умножения) на основу Чтобы перевести целую часть числа из системы с основанием p в систему с основанием q, необходимо разделить эту часть числа на q. Остаток от деления даст младший разряд числа в системе q. Полученную при этом долю необходимо снова разделить на q остаток даст следующий разряд числа и т. д. Для определения а 0 разделим А(10) на р. После деления получим частицу: и остаток от деленияа 0. 41

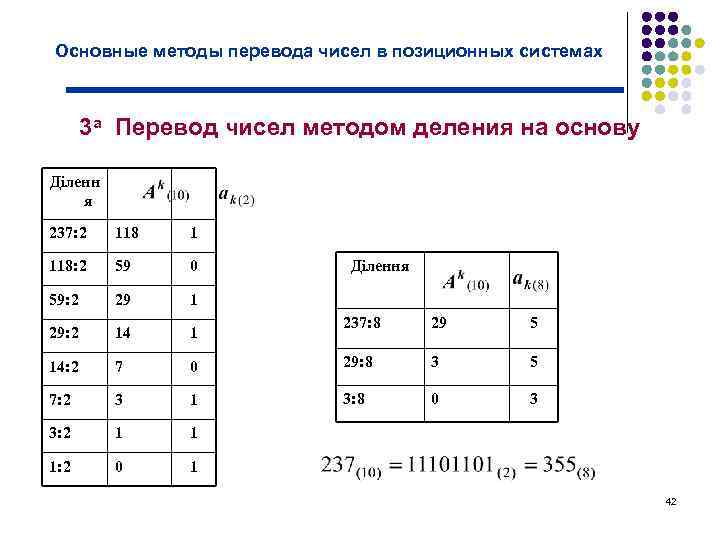Основные методы перевода чисел в позиционных системах 3 а Перевод чисел методом деления на Основные методы перевода чисел в позиционных системах 3 а Перевод чисел методом деления на основу Діленн я 237: 2 118 1 118: 2 59 0 59: 2 29 1 29: 2 14 1 14: 2 7 7: 2 Ділення 237: 8 29 5 0 29: 8 3 5 3 1 3: 8 0 3 3: 2 1 1 1: 2 0 1 42

Основные методы перевода чисел в позиционных системах 3 б Перевод чисел методом деления на Основные методы перевода чисел в позиционных системах 3 б Перевод чисел методом деления на основу Для перевода дробной части, ее необходимо умножить на q. Целая часть полученного произведения будет первым (после запятой, отделяющей целую часть от дробной) знаком в системе с основанием q. После отделения дробной части произведения, ее необходимо снова умножить на q. Целая часть полученного числа будет следующим знаком и т. д. Для того, чтобы определить первую цифру после запятой в новом представлении числа. В(10) умножим на р. После умножения получим Целая часть произведения дает значениеb-1. 43

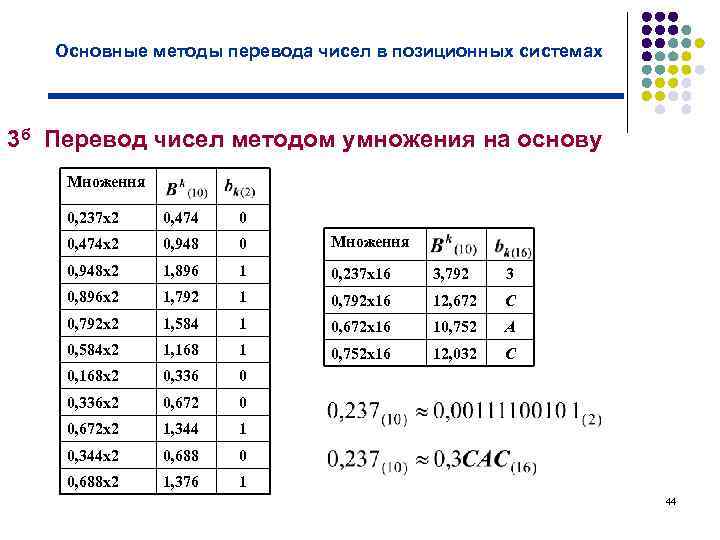Основные методы перевода чисел в позиционных системах 3 б Перевод чисел методом умножения на Основные методы перевода чисел в позиционных системах 3 б Перевод чисел методом умножения на основу Множення 0, 237 х2 0, 474 0 0, 474 х2 0, 948 0 Множення 0, 948 х2 1, 896 1 0, 237 х16 3, 792 3 0, 896 х2 1, 792 1 0, 792 х16 12, 672 С 0, 792 х2 1, 584 1 0, 672 х16 10, 752 А 0, 584 х2 1, 168 1 0, 752 х16 12, 032 С 0, 168 х2 0, 336 0 0, 336 х2 0, 672 0 0, 672 х2 1, 344 1 0, 344 х2 0, 688 0 0, 688 х2 1, 376 1 44

Основные методы перевода чисел в позиционных системах 4 метод вычитания степеней l l Из Основные методы перевода чисел в позиционных системах 4 метод вычитания степеней l l Из исходного числа с основанием р последовательно вычитается максимально допустимая степень числа с основанием q, умноженной на максимально возможный коэффициент, меньший основания q (например, для двоичной системы таким коэффициентом будет 1). Этот коэффициент и является значимой цифрой числа в новой системе. Пример (p = 10, q = 2) 237 – 27 = 109 – 26 = 45 – 25 = 13 – 23 = 5 – 22 = 1 – 20 = 237 – 128 = 109; 109 – 64 = 45; 45 – 32 = 13; 13 – 8 = 5; 5 – 4 = 1; 1 – 1 = 0. 0 1 1 2 1 0, 5 2 4 2 0, 25 3 8 3 0, 125 4 16 4 0, 0625 5 32 5 0, 03125 6 64 6 0, 015625 7 128 7 0, 0078125 8 256 8 0, 00390625 9 512 9 0, 001953125 10 1 024 10 0, 0009765625 11 2 048 11 0, 00048828125 12 4 096 12 0, 000244140625 Таким образом, можно записать ступенчатый ряд: 13 8 192 13 0, 0001220703125 237 = 1· 27 + 1· 26 + 1· 25 + 0· 24 + 1· 23 + + 1· 22 + 0· 21 + 1· 20. 14 16 384 14 0, 00006103515625 15 32 768 15 0, 000030517578125 16 65 536 16 0, 0000152587890625 237 = 3· 82 + 5· 81 + 5· 80. 45

Контрольные вопросы и задания для самопроверки l l l l l Что понимается под Контрольные вопросы и задания для самопроверки l l l l l Что понимается под системой счисления? В чем заключаются различия между позиционной и непозиционной системами счисления? Какие системы счисления могут быть отнесены к непозиционных? Каким образом записываются числа в римской системе счисления? Какие преимущества и недостатки десятичной, восьмеричной, шестнадцатеричной и двоичной систем счисления? Какая система счисления является наиболее экономной при представлении чисел и какая система счисления является наиболее удобной для использования в компьютерных системах и почему? Почему на практике почти не находят применения системы счисления с основанием более 16? Составьте таблицу, в которой перечислены все двоичные, троечные, восьмеричные и шестнадцатеричные числа от 0 до 32. Как определяется количество двоичных разрядов, необходимых для кодирования одной цифры произвольной позиционной системы счисления? 46 Выучите наизусть запись всех двоичных чисел от 0 до 32.