Лекция 2(1ч)_4сем(Гип-Бройля)новая версия 2013.ppt
- Количество слайдов: 14

Лекция 2(1 ч). Гипотеза де Бройля. Принцип неопределенности

Вопросы: • • • Двойственная корпускулярно-волновая природа света Гипотеза Л. де Бройля. Волновые свойства микрочастиц Эксперименты К. Дэвиссона и Л. Джермера по дифракции микрочастиц Принцип неопределенности В. Гейзенберга и его следствия Опыт Юнга с микрочастицами. «Парадокс» со щелями

Двойственная корпускулярно-волновая природа света

Эксперименты К. Дэвиссона и Л. Джермера по дифракции микрочастиц Волны де Бройля (волны материи) могут отражаться, преломляться, интерферировать друг с другом, испытывать дифракцию при взаимодействии с неоднородностями среды. В этом смысле можно говорить о дифракции частиц и наблюдать дифракционные эффекты в экспериментах с потоками (пучками) частиц в неоднородных средах. В 1927 г. американские физики Клинтон Дэвиссон и Лестер Джермер проводят серию опытов по дифракции электронов на кристалле. • Идея и схема эксперимента Если пучок ускоренных электронов обладает волновыми свойствами, то можно ожидать (даже не зная механизма отражения этих волн), что их отражение от кристалла будет иметь такой же интерференционный характер, как у рентгеновских лучей, для которых интерференционные максимумы отражения от атомных плоскостей наблюдаются при условии Вульфа – Брэггов (1913 г. ): 2 d sinα = mλ (m = 1, 2, …). 1 2 α 2’ 1’ d
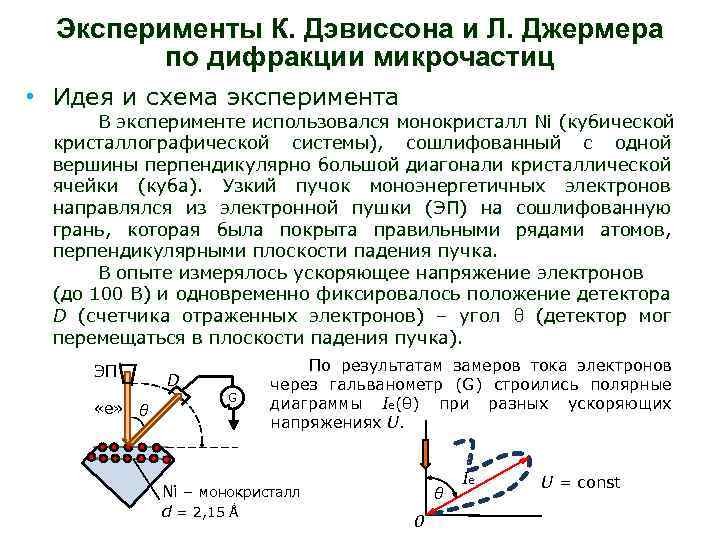
Эксперименты К. Дэвиссона и Л. Джермера по дифракции микрочастиц • Идея и схема эксперимента В эксперименте использовался монокристалл Ni (кубической кристаллографической системы), сошлифованный с одной вершины перпендикулярно большой диагонали кристаллической ячейки (куба). Узкий пучок моноэнергетичных электронов направлялся из электронной пушки (ЭП) на сошлифованную грань, которая была покрыта правильными рядами атомов, перпендикулярными плоскости падения пучка. В опыте измерялось ускоряющее напряжение электронов (до 100 В) и одновременно фиксировалось положение детектора D (счетчика отраженных электронов) – угол θ (детектор мог перемещаться в плоскости падения пучка). ЭП «е» θ D G По результатам замеров тока электронов через гальванометр (G) строились полярные диаграммы Ie(θ) при разных ускоряющих напряжениях U. Ni – монокристалл d = 2, 15 Ǻ θ 0 Ie U = const

Эксперименты К. Дэвиссона и Л. Джермера по дифракции микрочастиц • Результаты эксперимента Ie max 50˚ Ie Ie 0 U = 44 В 50˚ 0 U = 54 В 50˚ 0 U = 64 В Получив семейство полярных диаграмм, ученые из USA тщательно их проанализировали и пришли к выводу: отчетливый максимум Ie, наблюдаемый под углом θ = 50˚ и при ускоряющем напряжении U = 54 B соответствует интерференционному максимуму 1 -го порядка, полученному от отражательной плоской 1’ дифракционной решетки с известным периодом d. 1 2 2’ θ d

Эксперименты по дифракции микрочастиц • Опыты Дж. Томсона и П. С. Тартаковского В 1927 г. Джордж Томсон (UK) осуществил опыты с быстрыми электронами (~ 10 кэ. В), а коллектив под руководством Петра С. Тартаковского (СССР) – со сравнительно медленными электронами (до 1, 7 кэ. В) по «просвечиванию» ими металлических фольг. В обоих экспериментах были получены дифракционные картины (по «методу Дебая» ) в виде системы колец при прохождении электронных пучков через поликристаллическую фольгу (последняя получалась спеканием из металлического порошка). Фольга «е» N S Кроме того, было установлено воздействие внешнего магнитного поля на дифрагированные лучи – они заметно отклонялись, что свидетельствовало об их электронной природе. Замечание. Позднее на специальных установках были получены дифракционные эффекты на нейтронах, протонах, атомных и молекулярных пучках – им всем присущи волновые свойства!

Принцип неопределенности • Соотношения неопределенностей Гейзенберга В классической механике полное описание состояния частицы (как материальной точки) определяется динамическими параметрами, такими как координата (x, y, z), импульс (px, py, pz), момент импульса (Lx, Ly, Lz), энергия (Е) и др. Для материальной точки в каждый момент времени эти параметры однозначно определены и могут быть измерены. Однако анализ реального поведения микрочастицы показывает, что существует принципиальный предел точности, с которой подобные переменные могут быть указаны и измерены макроскопическими приборами. Этот предел часто называют принципом неопределенности. В 1927 г. немецкий физик Вернер Гейзенберг выдвинул идею о принципиальной невозможности одновременного точного измерения определенных пар связанных между собой характеристик (канонически сопряженных величин) частицы. В. Гейзенберг установил, что при наличии у микрочастицы волновых свойств, существует связь (соотношения) между неопределенностями координат и соответствующими неопределенностями компонент импульса частицы:

Принцип неопределенности λ 0 λ
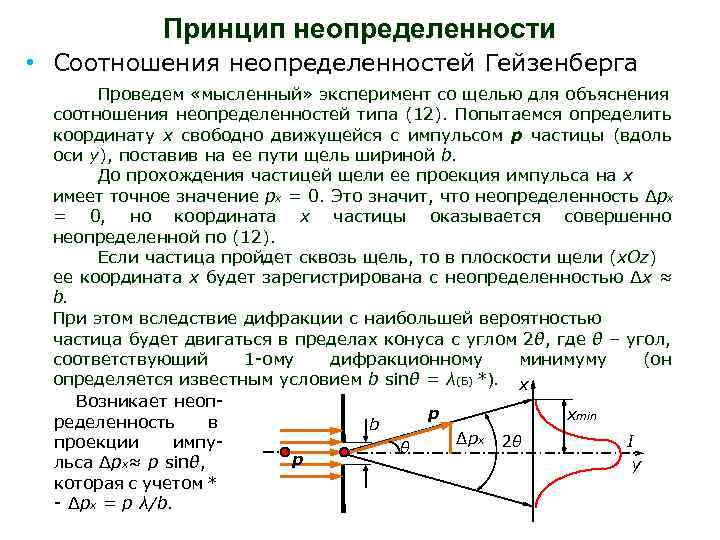
Принцип неопределенности • Соотношения неопределенностей Гейзенберга Проведем «мысленный» эксперимент со щелью для объяснения соотношения неопределенностей типа (12). Попытаемся определить координату х свободно движущейся с импульсом р частицы (вдоль оси y), поставив на ее пути щель шириной b. До прохождения частицей щели ее проекция импульса на х имеет точное значение рх = 0. Это значит, что неопределенность Δрх = 0, но координата х частицы оказывается совершенно неопределенной по (12). Если частица пройдет сквозь щель, то в плоскости щели (x. Oz) ее координата х будет зарегистрирована с неопределенностью Δх ≈ b. При этом вследствие дифракции с наибольшей вероятностью частица будет двигаться в пределах конуса с углом 2θ, где θ – угол, соответствующий 1 -ому дифракционному минимуму (он определяется известным условием b sinθ = λ(Б) *). x Возникает неопp xmin ределенность в b Δpx 2θ I проекции импуθ p льса Δрх≈ р sinθ, y которая с учетом * - Δрх = р λ/b.

Принцип неопределенности и его следствия • Соотношения неопределенностей Гейзенберга С учетом того, что было принято Δх ≈ b, а из определения длины волны де Бройля – р = 2πh / λ, можно записать соотно шение неопределенностей: Таким образом, попытка определить координату х частицы действительно привела к появлению неопределенности Δрх. • Следствия из принципа неопределенности 1. Невозможно состояние, в котором частица находилась бы в покое (так как при этом было бы р=0 и Δр = 0). 2. При рассмотрении движения квантового объекта необходимо во многих случаях отказываться от понятия «траектория» (так как всегда есть Δх ≠ 0 и провести однозначную траекторию не возможно). 3. Часто для микрочастицы теряет смысл деление полной энергии Е на потенциальную U и кинетическую К (так как U – зависит от координат, а К – зависит от импульса). 4. В квантовой механике, принципиально, не существуют изолированные системы (их невозможно создать), так как положение квантовой системы в пространстве всегда в той или иной степени неопределенно.

Опыт Юнга с электронами (http: //www. youtube. com/watch? v=QGq 2 YNy. Vb. Gs http: //www. youtube. com/watch? v=v 2 J 4 l. JAvp. LM http: //www. youtube. com/watch? v=t. Yc 9 VSYX 8 P 8 )

Опыт Юнга с электронами. «Парадокс» со щелями В начале проведем «мысленный» эксперимент, аналогичный опыту Юнга в оптике. Пусть пучок электронов испускается электронной пушкой в направлении преграды Д с двумя щелями А и В, а за преградой расположен экран Э, на котором регистрируется распределение попавших электронов. С позиций классической механики и статистики должны получить распределения: • а) – в случае открытой только щели А; • b) – в случае открытой только щели В; • c) – в случае двух открытых щелей А и В (как сумма отдельных распределений). Э a Д A ē c I O B b
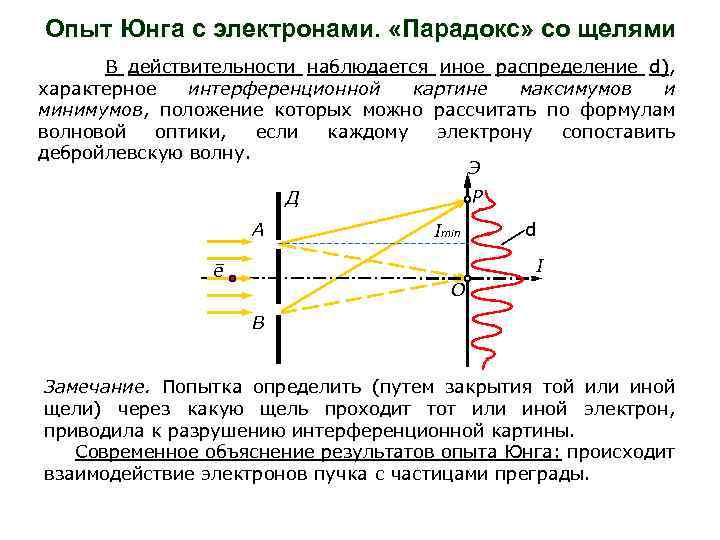
Опыт Юнга с электронами. «Парадокс» со щелями В действительности наблюдается иное распределение d), характерное интерференционной картине максимумов и минимумов, положение которых можно рассчитать по формулам волновой оптики, если каждому электрону сопоставить дебройлевскую волну. Э P Д A Imin d I ē O B Замечание. Попытка определить (путем закрытия той или иной щели) через какую щель проходит тот или иной электрон, приводила к разрушению интерференционной картины. Современное объяснение результатов опыта Юнга: происходит взаимодействие электронов пучка с частицами преграды.
Лекция 2(1ч)_4сем(Гип-Бройля)новая версия 2013.ppt