ЛЕКЦИЯ 16. Основы атомной физики.ppt
- Количество слайдов: 31

ЛЕКЦИЯ 16. ОСНОВЫ АТОМНОЙ ФИЗИКИ 1 Водородоподобные атомы в квантовой механике 1

Стационарное уравнение Шредингера для водородоподобного атома Стационарное уравнение Шредингера, описывающее квантовое состояние электрона в атоме, имеет вид Данная задача обычно решается в сферической системе координат, в которой лапласиан имеет довольно громоздкий вид: 2
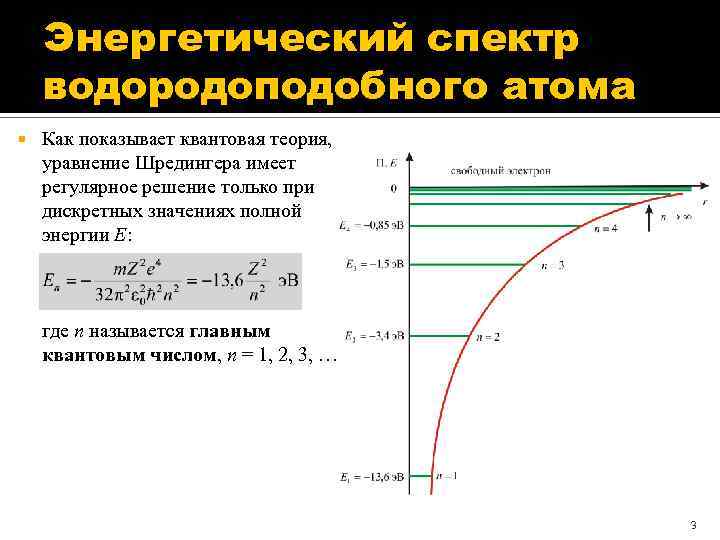
Энергетический спектр водородоподобного атома Как показывает квантовая теория, уравнение Шредингера имеет регулярное решение только при дискретных значениях полной энергии E: где n называется главным квантовым числом, n = 1, 2, 3, … 3

ЛЕКЦИЯ 16. ОСНОВЫ АТОМНОЙ ФИЗИКИ 2 Квантовые числа 4

Главное квантовое число Как уже отмечалось ранее, главное квантовое число n = 1, 2, 3, … определяет дискретные значения полной энергии E электрона в заданном квантовом состоянии: 5

Орбитальное квантовое число Орбитальное (азимутальное) квантовое число l , принимающее следующие целочисленные значения: 0, 1, 2, … (n – 1), определяет возможные значения модуля орбитального момента импульса L движущегося в атоме электрона: и связанный с таким движением магнитный момент где = e/2 m – гиромагнитное отношение для орбитального движения, равное, а универсальная постоянная служит единицей измерения магнитных моментов атомов и называется магнетоном Бора 6

Магнитное квантовое число ml , принимающее значения 0, 1, 2, …, l, определяет возможные значения проекции орбитального момента импульса Lz электрона, а также проекции магнитного момента электрона, связанного с его движением в атоме: Под проекциями Lz и l, z понимаются проекции на выделенное в пространстве направление Z. Обычно это направление выделяется внешним магнитным полем или электрическим полем. 7

Символические обозначения квантовых состояний электрона Для обозначения квантовых состояний электрона с заданным значением орбитального квантового числа l используются следующие спектроскопические символы: Значение l 0 1 2 3 4 5 … Символ состояния s p d f g h … В частности, состояния с l = 0 называется s-состоянием, а электрон в таком состоянии – s-электроном; состояние с l = 1 называется p-состоянием и т. д. Для более полного обозначения перед символом состояния указывается значение главного квантового числа n. Так, электрон в квантовом состоянии с n = 2 и l = 0 обозначается символом 2 s, а в состоянии с n = 4 и l = 2 – символом 4 d и т. д. 8
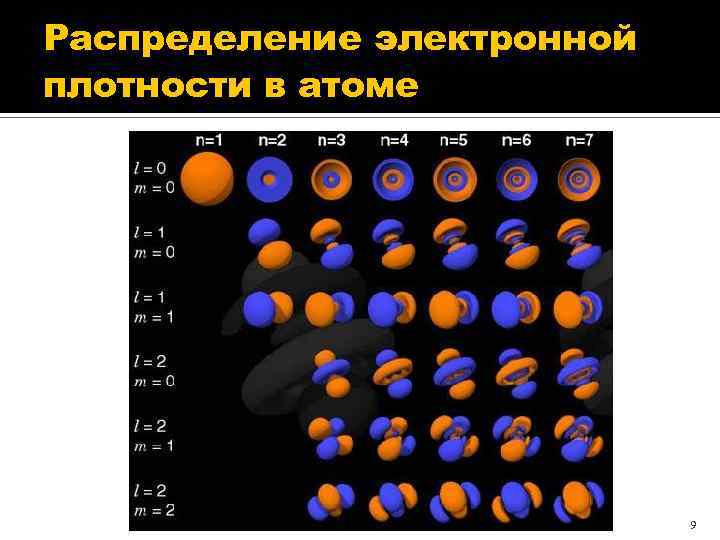
Распределение электронной плотности в атоме 9

Основное и возбужденные состояния водородоподобного атома Состояние с наименьшей энергией электрона (1 s) называется основным состоянием электрона (атома), а все остальные – возбужденными состояниями. При переходе из состояния с главным квантовым числом n 1 в состояние с главным квантовым числом n 2 водородоподобный атом излучает на частоте Причем, согласно правилам отбора, не все переходы возможны, а лишь те, для которых выполняется условие l = 0, 1 10

Спин электрона Для согласования квантовой теории с экспериментом сначала в виде гипотезы (С. Гаудсмит, Дж. Уленбек, 1925 г. ), а позже как следствие релятивистской квантовой механики (П. Дирак, 1928 г. ) вводится четвертое квантовое число – спиновое квантовое число ms = s, где спин электрона s = ½. Спин электрона характеризует собственные, т. е. никак не связанные с движением электрона в атоме, механический и магнитный моменты: Спиновое квантовое число определяет возможные проекции этих моментов на выделенное направление в пространстве: 11

Полный момент импульса электрона. Правила отбора Сумма орбитального момента импульса Ll и спинового (собственного) момента импульса Ls дают полный момент импульса электрона в атоме где j – квантовое число полного момента При электронных переходах в атоме для квантового числа j выполняется правило отбора, определяющее возможные изменения этого числа для таких переходов: j = 0, 1. Число квантовых состояний, соответствующих заданному значению главного квантового числа n называется кратностью вырождения энергетического уровня атома. Оно равно 12
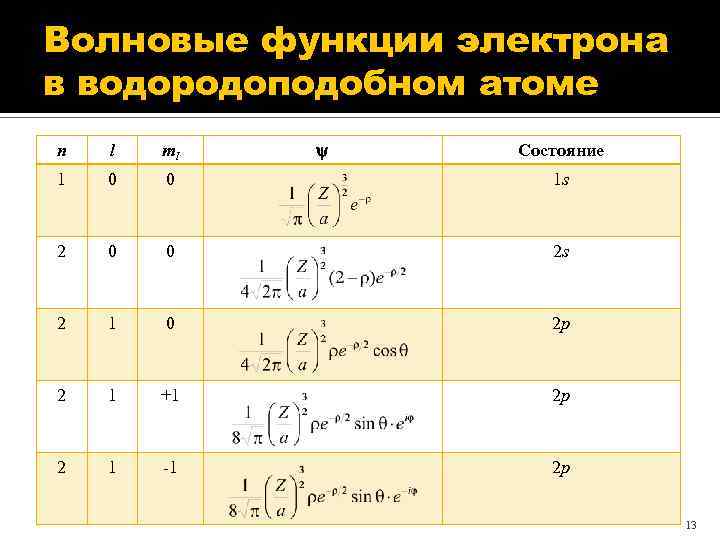
Волновые функции электрона в водородоподобном атоме n l ml Состояние 1 0 0 1 s 2 0 0 2 s 2 1 0 2 p 2 1 +1 2 p 2 1 -1 2 p 13

ЛЕКЦИЯ 164. ОСНОВЫ АТОМНОЙ ФИЗИКИ 3 Многоэлектронные атомы 14

Метод самосогласованного поля Приближенный метод решения уравнения Шредингера для многоэлектронных атомов был разработан английским физиком Д. Хартри и развит советским физиком В. А. Фоком. Метод получил название метода самосогласованного поля. Состояние каждого из N электронов в атоме описывается волновой функцией (ri), определяемой своими 4 -мя квантовыми числами n, l, ml и ms, а волновая функция всех N электронов представляется в виде произведения В нулевом приближении волновые функции (ri) , берутся из набора волновых функций водородоподобного атома с Z = N, т. е. считается, что на движение каждого электрона остальные электроны не влияют. 15

Метод самосогласованного поля. Принцип Паули Затем определяется энергия взаимодействия каждого электрона со всеми остальными: Эта потенциальная энергия вводится в виде поправки в уравнение Шредингера и для каждого электрона снова решается такое уравнение. С помощью волновых функций снова вычисляются поправки к энергии электронов и такие операции повторяются до тех пор, пока результаты не станут самосогласованными, т. е. последующие результаты не будут с достаточной точностью совпадать с предыдущими. В. А. Фок учел при расчетах принцип запрета Паули так, чтобы в комбинации квантовых чисел у разных электронов не встречалось 4 одинаковых квантовых числа 16

Электронная конфигурация атома Электронную конфигурацию многоэлектронного атома описывают, указывая для каждого электрона значения главного и орбитального квантовых чисел. При этом число электронов с одинаковыми квантовыми числами n и l указывается в виде показателя степени. Например, электронная конфигурация нормального квантового состояния атома кислорода (N = 8) записывается в виде: 1 s 224. Это означает, что 2 электрона находятся в состоянии с n = 1 и l = 0, еще 2 электрона в состоянии с n = 2 и l = 0, и, наконец, 4 электрона – в состоянии с n = 2 и l = 1. Совокупность состояний с одинаковыми n и l образуют электронную оболочку. Электронные оболочки объединяются в электронные слои с одинаковым значением квантового числа n электронов. Число электронов, полностью заполняющих слой, равно 2 n 2. Слои с квантовыми числами n = 1, 2, 3, 4, 5 … соответственно обозначаются символами K, L, M, N, O, … 17

Орбитальный, спиновый и полный моменты атома В сложном многоэлектронном атоме при сложении механических и магнитных моментов в результирующий момент атома возможны 2 типа связей. В случае JJ-связи (наблюдается обычно у тяжелых атомов) орбитальный Ll и спиновый Ls моменты каждого электрона складываются в суммарный момент Lj. Затем эти моменты объединяются в результирующий момент атома. В наиболее часто встречающемся случае (легкие и средние атомы) LS -связи такая связь организуется по другой схеме. 18

Орбитальный момент испульса атома 1. Все орбитальные моменты импульса Ll отдельных электронов складываются в результирующий орбитальный момент импульса атома Здесь квантовое число орбитального момента атома является целым числом, либо нулем (сумма магнитных квантовых чисел ml электронов) 19

Спиновый момент импульса атома 2. Спиновые моменты импульса Ls всех электронов складываются в суммарный спиновый момент импульса атома Здесь S – квантовое число спинового момента импульса атома (сумма спиновых квантовых чисел ms электронов) В атомах с четным числом электронов N квантовое число S принимает все целые значения от нуля до ½ N. При нечетном числе электронов N квантовое число S может принимать все полуцелые значения от ½ до ½ N 20

Полный момент атома 3. Результирующий полный момент импульса атома есть результат квантово-механического сложения орбитального и спинового моментов импульса LL и LS. Его значение определяется по формуле Проекция полного момента импульса атома на выделенное направление Z определяется следующей формулой Здесь J и m. J – соответствующие квантовые числа полного момента импульса атома и его проекции на ось Z. 21

Магнитный момент атома. Фактор Ланде Результирующий магнитный момент многоэлектронного атома, а также его проекция на выделенное направление Z, в частности, на направление внешнего магнитного поля, определяется как Здесь B – магнетон Бора, а множитель называется множителем или фактором Ланде. Для заданного значения J (т. е. для заданного состояния атома) существует 2 J +1 различных ориентаций магнитного момента по отношению к внешнему магнитному полю 22

Правила отбора Для квантового числа m. J выполняются правила отбора: при переходе атома из одного состояния в другое возможны только такие переходы, для которых 23

Терм атома Для обозначения определенного квантового состояния (основного и возбужденных) многоэлектронного атома используется условное обозначение – «терм» атома в виде Число 2 S + 1 называется мультиплетностью состояния, а под L подразумевается одна из букв таблицы: L 1 2 3 4 5 … Символ состояния 0 S P D F G H … Например, для терма 4 D 1/2 значения квантовых чисел L = 2, S = 3/2, J = 1/2, а для терма 5 F 2 , соответственно, L = 3, S = 2 и J = 2. 24

Основное состояние атома: правила Хунда 1. Из состояний атома с заданной электронной конфигурацией ниже по энергии те, которые отвечают большим значениям S. 2. Из состояния атома с заданной конфигурацией и заданным спиновым числом S ниже по энергии те, которые отвечают большему значению квантового числа L. 25
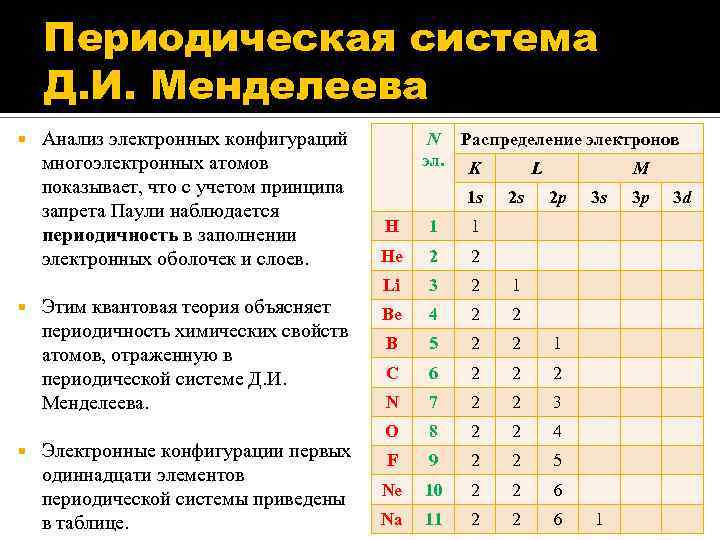
Периодическая система Д. И. Менделеева Анализ электронных конфигураций многоэлектронных атомов показывает, что с учетом принципа запрета Паули наблюдается периодичность в заполнении электронных оболочек и слоев. Этим квантовая теория объясняет периодичность химических свойств атомов, отраженную в периодической системе Д. И. Менделеева. Электронные конфигурации первых одиннадцати элементов периодической системы приведены в таблице. N Распределение электронов эл. K L M 1 s 2 s 2 p H 1 2 3 2 1 Be 4 2 2 B 5 2 2 1 C 6 2 2 2 N 7 2 2 3 O 8 2 2 4 F 9 2 2 5 Ne 10 2 2 6 Na 11 2 2 6 3 d 2 Li 3 p 1 He 3 s 1 26

ЛЕКЦИЯ 4. ОСНОВЫ АТОМНОЙ ФИЗИКИ 4. 7 Излучение атомов 27

Частоты излучения атомов Спектры излучения атомов, содержащих большое число электронов, достаточно сложны и разнообразны. Основные частоты излучения таких атомов лежат в ИК-диапазоне и в диапазоне видимого света. Близким к водородному являются спектры излучения щелочных металлов, у которых имеет один внешний электрон, находящийся вне замкнутых электронных оболочек, которые частично экранируют электрическое поле ядра. При этом энергия внешнего электрона зависит не только от значения квантового числа n, от и от значения орбитального числа l. Так, например для частот атомов Na (переход 2 1) достаточно хорошо выполняется соотношение Поправочный коэффициент a 1 = 1, 35 для s-состояний, (l = 0); a = 0, 87 для pсостояний (l = 1); a = 0, 01 для d-состояний (l = 2). Для состояний с большими значениями l поправочный коэффициент a = 0. 28

Спектры излучения молекул При соединении атомов в молекулы и твердые тела (кристаллы) внешние электронные оболочки атомов искажаются. Поэтому оптические и ИК-спектры излучения молекул и кристаллов сильно отличаются от спектров излучения одиночных атомов. В молекулах возможны колебательные и вращательные движения отдельных атомов. Поэтому молекулярные спектры кроме дискретных спектральных линий содержат ряд очень близкий линий, образующих многолинейчатый или полосатый спектр. Спектры излучения твердых тел становятся практически непрерывными (сплошными). 29

Спектры испускания и поглощения веществ При пропускании излучения со сплошным спектром через газообразное вещество наблюдаются линии поглощения на тех же частотах, на которых это вещество излучает. Соответствие спектров испускания и спектров поглощения следует из квантовой теории излучения атомов. В настоящее время составлены атласы спектров излучения значительного числа атомов, молекул и твердых тел. С помощью таких атласов можно проводить спектральный анализ, когда на основании изучения спектрального состава излучения можно сделать вывод о химическом составе излучающего вещества. Такой же вывод можно сделать при изучении спектров поглощения. 30

Характеристическое рентгеновское излучение. Закон Мозли Атомы могут излучать электромагнитное излучение и в результате переходов во внутренних оболочках, если, например эти атомы бомбардировать пучком электронов достаточно больших энергий. После удаления электрона атома с внутреннего слоя на освободившееся место переходят электроны с более высоких энергетических слоев. При этом атом излучает характеристическое рентгеновское излучение в втде отдельных спектральных линий. Для частоты отдельной серии такого излучения справедлив закон Мозли: Здесь R – постоянная Ридберга, Z – порядковый номер элемента (атома), постоянная экранирования (имеет свое значение для каждой серии). Эти серии носят название K-серии (n 1 = 1), L – серии (n 1 = 2) и т. д. Важность закона Мозли состоит в том, частота характеристического спектра излучения зависит от порядкового номера Z атома, что позволяет экспериментально 31 устанавливать химический состав излучающего вещества.
ЛЕКЦИЯ 16. Основы атомной физики.ppt