Лекція 14 Робота та енергія електричного поля 1

Лекція 14. Робота та енергія електричного поля 1. Енергія системи зарядів 2. Енергія зарядженого провідника 3. Енергія зарядженого конденсатора 4. Енергія електричного поля: а) поле зарядженої кулі, б) поле зарядженого кільця, в) поле зарядженого провідника в формі квадрата. 5. Електрокапілярний ефект

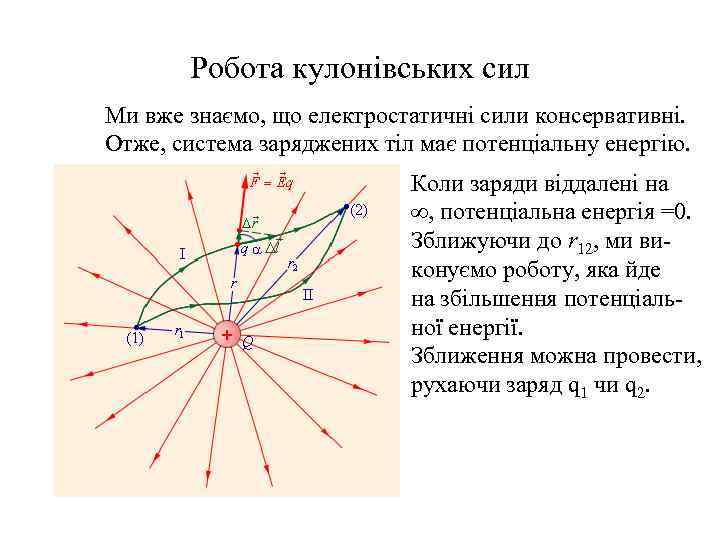
Робота кулонівських сил Ми вже знаємо, що електростатичні сили консервативні. Отже, система заряджених тіл має потенціальну енергію. Коли заряди віддалені на ∞, потенціальна енергія =0. Зближуючи до r 12, ми виконуємо роботу, яка йде на збільшення потенціальної енергії. Зближення можна провести, рухаючи заряд q 1 чи q 2.

Робота кулонівських сил • В обох випадках робота одна і та ж. Ця робота відповідає потенціальній енергії системи Тепер в систему добавимо третій заряд. Виконаємо роботу q 2 r 23 r 12 q 3 q 1 r 13 φ3 – потенціал, який створюють заряди q 1 i q 2 в точці q 3.

Робота кулонівських сил • Разом з А 1 чи А 2 енергія системи трьох зарядів потенціали, які створюють інші заряди в точці qi.

Робота кулонівських сил • Для довільної кількості зарядів потенціал, створений іншими зарядами в точці qi.

Енергія зарядженого провідника • Будемо переносити на провідник заряд частинами dq. Тоді d. W = d. A = φdq=qdq/C, φ – потенціал провідника, зумовлений наявністю заряду q. • Звідси енергія Тут ми вважали, що енергія незарядженого провідника дорівнює нулю. Враховуючи, що q = Cφ, отримаємо:

Енергія зарядженого конденсатора • Процес появи заряду на конденсаторі уявляють як перенесення заряду dq від однієї обкладки до іншої. Тоді Для конденсатора Тому Цей результат можна отримати, враховуючи взаємодію заряду з потенціалом

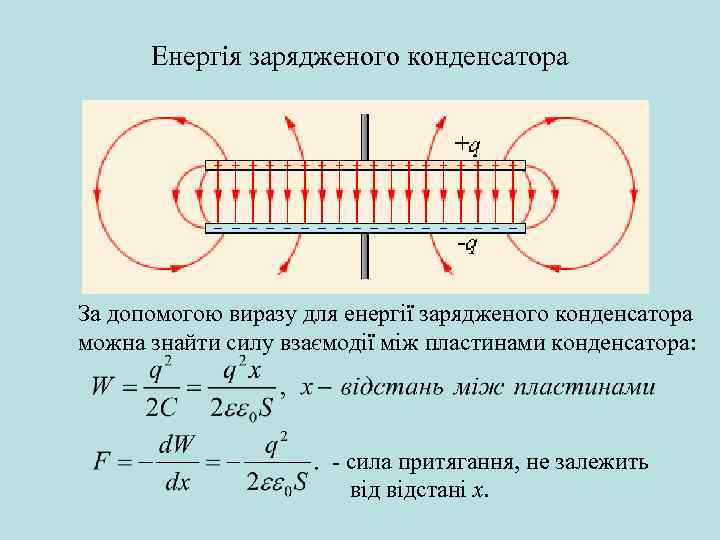
Енергія зарядженого конденсатора За допомогою виразу для енергії зарядженого конденсатора можна знайти силу взаємодії між пластинами конденсатора: - сила притягання, не залежить відстані х.

Енергія зарядженого конденсатора • Силу можна знайти як взаємодію заряду однієї пластини з полем іншої пластини: А якщо діелектрик має товщину d 1, меншу відстані між пластинами d? В такому разі маємо два послідовно з'єднані конденсатори.

Енергія зарядженого конденсатора • Розглянемо випадок, коли діелектрик входить між пластинками конденсатора. В цьому випадку конденсатор складається з двох паралельно з'єднаних конденсаторів, загальна ємність яких дорівнює частина площі, зайнятої діелектриком. Якщо конденсатор заряджений і від’єднаний від джерела напруги (q = const), тоді

Енергія зарядженого конденсатора • Зі збільшенням х енергія зменшується. Отже, електричне поле буде втягувати діелектрик між пластини конденсатора. Сила втягування При х = 0 сила втягування буде максимальною. При вертикальній орієнтації конденсатора втягування відбудеться, якщо ця сила переважає силу тяжіння діелектрика.

Енергія зарядженого конденсатора Якщо конденсатор залишається під’єднаним до зовнішнього джерела напруги, тоді енергія зарядженого конденсатора росте зі збільшенням х. Отже, в цьому випадку на діелектрик буде діяти сила виштовхування, величина якої не залежить від х.

Енергія електричного поля • Енергія конденсатора Ця формула пов'язує енергію конденсатора з напруженістю електричного поля на відміну від формули яка пов'язує енергію з зарядом. Отже, виникає питання: де локалізована енергія? На поверхні (заряди) чи в об'ємі (поле)?

Енергія електричного поля • Висновок робимо на підставі того, що поля існують і без зарядів (електромагнітне поле) і переносять енергію. Тому прийшли до висновку, що носієм енергії є поле. • Якщо поле однорідне, як в конденсаторі, то енергія розміщена в об'ємі з постійною густиною Така формула справедлива і для неоднорідного поля. Оскільки D = εεo. E,

Енергія електричного поля • Оскільки Перший член справа відповідає густині енергії в вакуумі, а другий – енергії поляризації середовища. Робота, витрачена на поляризацію одиничного об'єму

Поле зарядженої кулі • Поле зарядженої кулі в діелектричному середовищі • Для визначення енергії поля проінтегруємо за безмежним об'ємом. Отже, такий же результат, як і для зарядженого провідника.

Поле зарядженого кільцевого провідника • Провідник, зігнутий у формі кільця, зарядили зарядом q. Оскільки маємо рівномірний розподіл заряду з лінійною густиною λ, то потенціал в центрі R кола Енергія заряду q‘ в цьому полі

Поле зарядженого кільцевого провідника • Тепер знайдемо енергію поля на осі обертання кільця. Нехай точка М знаходиться на відстані х R від центра кільця. В цьому разі β x M

Поле зарядженої нитки в формі квадрата • Розглянемо рівномірно заряджений стрижень, зігнутий у формі квадрата зі стороною а. Знайдемо поле в центрі квадрата. Врахуємо, що q = 4 aλ, dq=λdℓ, α r

Електрокапілярний ефект • Надамо пластинкам конденсатора з повітряним зазором заряди q і -q. Ємність C=εo. S/d. Енергія Wo = q 2/2 Co. • Тепер зануримо нижній край конденсатора в рідкий діелектрик. Діелектрик підніметься вгору між пластинками конденсатора. Отримаємо два паралельно підключені конденсатори з загальною ємністю При цьому енергія поля зменшиться, отже підняття рідини є енергетично вигідним.

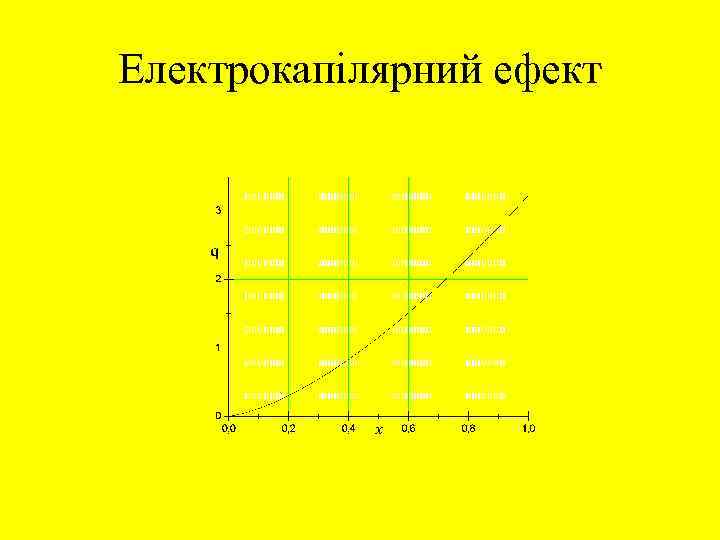
Електрокапілярний ефект • Остаточно знаходимо Величина константи А залежить від технічних даних рідини та конденсатора, тому для конкретного випадку її легко порахувати. Максимальне значення функції зліва = ε 2. Отже, можна знайти заряд qm, необхідний для повного заповнення конденсатора рідиною. Функцію f(x) можна протабулювати в залежності від величини х, а потім знайти відповідну величину q.

Електрокапілярний ефект • Збільшується потенціальна енергія рідини в полі тяжіння. Стовпчик рідини установиться на рівні, який відповідає мінімуму сумарної енергії. Явище схоже на капілярний ефект. • Сумарна енергія ρ – густина рідини, х – частина площі конденсатора, яка контактує з рідиною, а – висота конденсатора. Мінімум енергії знайдемо, прирівнявши похідну до нуля:

Електрокапілярний ефект