Лекция 14 ЭЛЕМЕНТЫ ФИЗИЧЕСКОЙ КИНЕТИКИ 1 Процессы релаксации

Лекция 14. ЭЛЕМЕНТЫ ФИЗИЧЕСКОЙ КИНЕТИКИ 1. Процессы релаксации. 2. Роль столкновений. Эффективный диаметр молекул. Средняя длина свободного пробега молекул в газах. 3. Диффузия газов. Закон Фика. Коэффициент самодиффузии. 4. Теплопроводность газов. Уравнение Фурье. Коэффициент теплопроводности. 5. Внутреннее трение. Уравнение Ньютона. Коэффициент вязкости.

Процессы релаксации Если система не находится в термодинамическом равновесии, то она стремится к нему и в конечном счете переходит в состояние термодинамического равновесия. Самопроизвольный процесс перехода системы в состояние т/д равновесия называется релаксацией, а время перехода – временем релаксации. Время релаксации относится к числу нечетко определенных понятий. При нарушении равновесия в системе возникают процессы переноса энергии (теплопроводность), вещества (диффузия) или импульса (вязкое трение). Все эти процессы являются необратимыми.

Раздел физики, изучающий эти процессы, называется физической кинетикой. В общем случае рассмотрение таких процессов – дело очень сложное. Ситуация сильно упрощается в случае разреженных газов. Для таких газов выполняются следующие условия. 1. Большую часть времени каждая молекула находится далеко от других молекул и не взаимодействует с ними. 2. Рассматриваются попарные взаимодействия молекул, то есть взаимодействия двух молекул. 3. Среднее расстояние между молекулами существенно больше их размера.

Роль столкновений. Газокинетический диаметр молекул. Средняя длина свободного пробега. Средняя скорость теплового движения молекул : Если бы молекулы двигались прямолинейно с такими скоростями, то , например, запах пахучего вещества распространялся бы мгновенно в пределах одной комнаты. Однако этого не происходит. Медленность диффузии в данном примере (и аналогичных явлениях) связана со столкновениями молекул. Свободно молекула пролетает короткое расстояние до

следующего столкновения. В момент столкновения скорость молекулы испытывает резкое изменение как по величине, так и по направлению. В результате траектория молекулы – ломаная линия с большим числом звеньев. Для количественного описания движения молекул введем: 1. Среднее время свободного пробега - среднее время движения молекулы до следующего столкновения.

2. Среднюю длину свободного пробега среднее расстояние, которое пролетает молекула между соседними столкновениями. В данном рассмотрении не будем учитывать распределение молекул по скоростям, считая, что они движутся с одинаковой по модулю средней скоростью. Тогда: Для краткости записи в дальнейшем оставим знак усреднения только у скорости. Тогда:

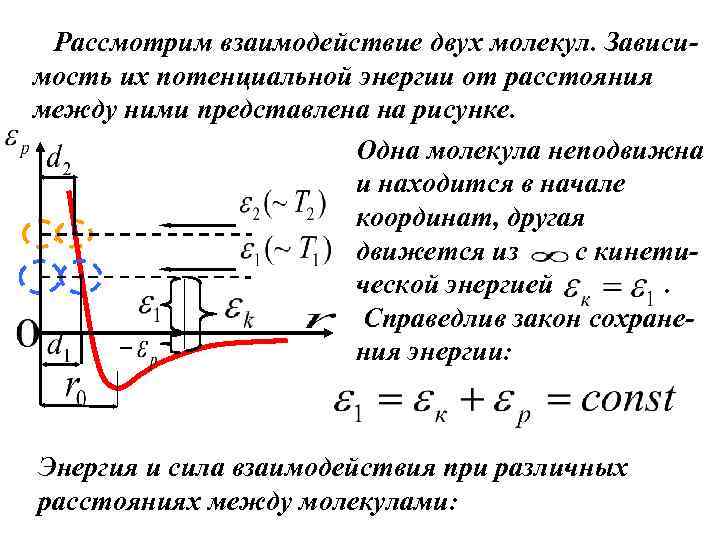Рассмотрим взаимодействие двух молекул. Зависимость их потенциальной энергии от расстояния между ними представлена на рисунке. Одна молекула неподвижна и находится в начале координат, другая движется из с кинетической энергией. Справедлив закон сохранения энергии: Энергия и сила взаимодействия при различных расстояниях между молекулами:

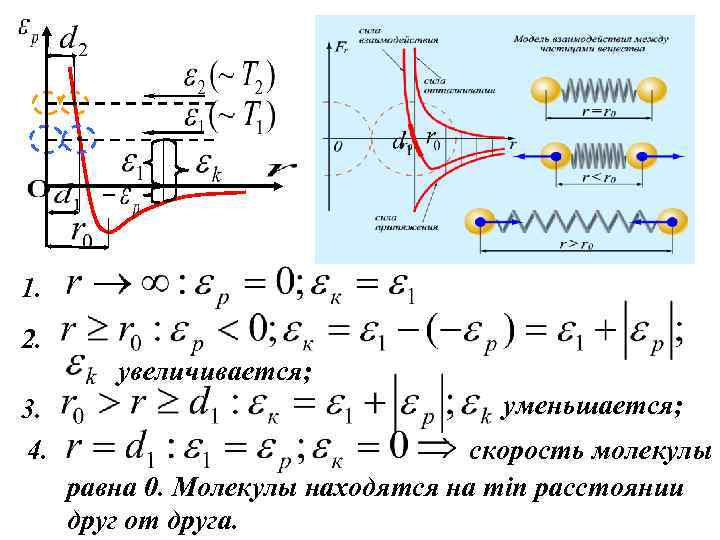1. 2. увеличивается; 3. 4. уменьшается; скорость молекулы равна 0. Молекулы находятся на min расстоянии друг от друга.

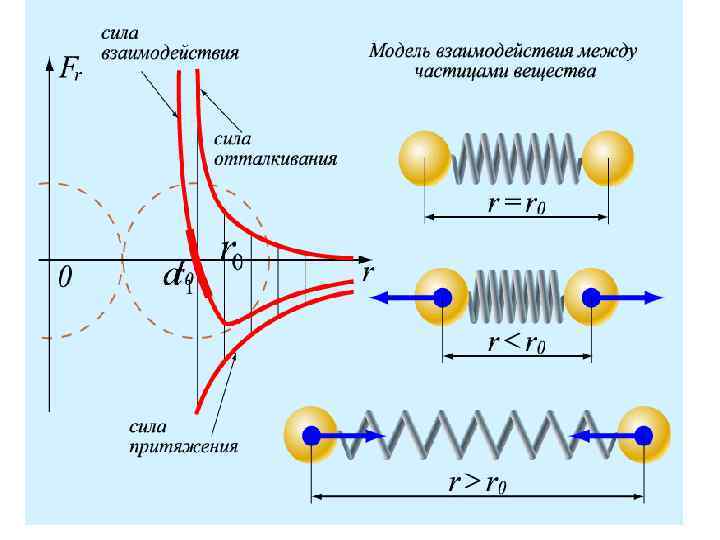
Минимальное расстояние, на которое сближаются центры двух молекул, называется эффективным (или газокинетическим) диаметром молекулы: Из графика видно, что зависит от энергии движущейся молекулы ( при ), но эта зависимость очень слабая, поэтому в дальнейшем она не будет учитываться. Величина называется эффективным сечением.

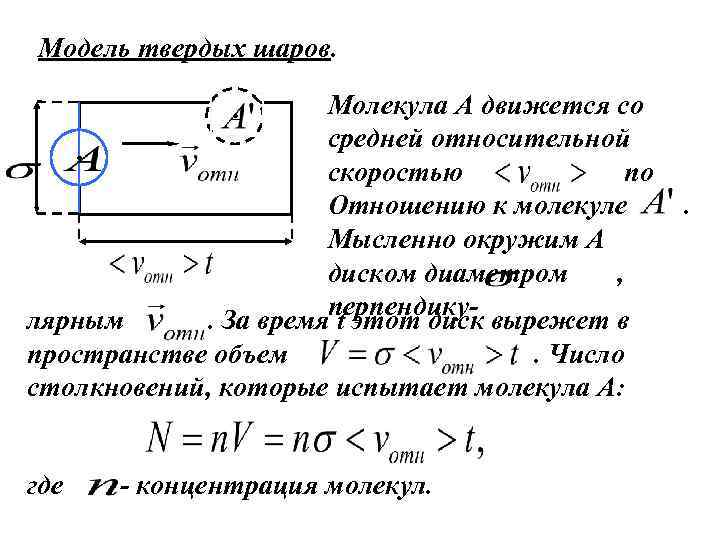Модель твердых шаров. Молекула А движется со средней относительной скоростью по Отношению к молекуле Мысленно окружим А диском диаметром , перпендику- вырежет в. За время t этот диск лярным пространстве объем. Число столкновений, которые испытает молекула А: где - концентрация молекул. .

Можно показать, что . Тогда Если происходит одно столкновение (N=1 и ) Среднее время свободного пробега Средняя длина свободного пробега

Из основного уравнения МКТ: , подставим в Число столкновений одной молекулы за 1 секунду: Полное число столкновений за 1 сек. в единице объема

Рассмотрим пример. Рассчитать , , для кислорода при температуре T=300 K и давлении , если диаметр молекулы

Процессы переноса Введем понятие потока частиц : это число молекул, проходящих через площадку единичной площади, перпендикулярную к их скорости, за единицу времени. Пользуясь рисунком, легко получить где - концентрация молекул; - средняя скорость теплового движения. Размерность

Диффузия газов Диффузия от латинского diffusio – распространение, растекание взаимное проникновение соприкасающихся веществ друга, вследствие теплового движения частиц вещества. Диффузия происходит в направлении уменьшения концентрации вещества и ведет к его равномерному распределению по занимаемому объему.

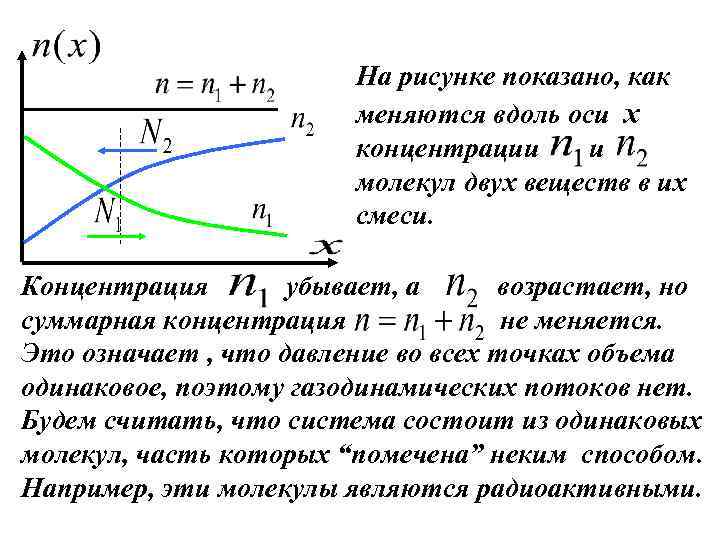. На рисунке показано, как меняются вдоль оси x концентрации и молекул двух веществ в их смеси. z Концентрация убывает, а возрастает, но суммарная концентрация не меняется. Это означает , что давление во всех точках объема одинаковое, поэтому газодинамических потоков нет. Будем считать, что система состоит из одинаковых молекул, часть которых “помечена” неким способом. Например, эти молекулы являются радиоактивными.

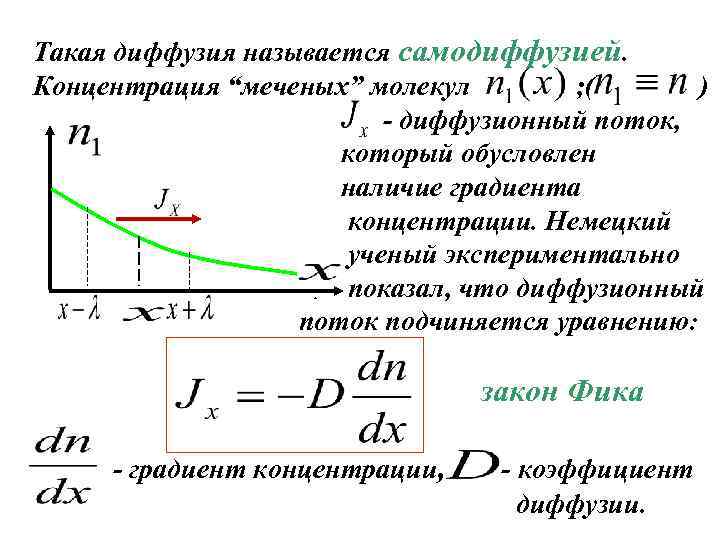Такая диффузия называется самодиффузией. Концентрация “меченых” молекул ; ( ) - диффузионный поток, который обусловлен наличие градиента концентрации. Немецкий ученый экспериментально показал, что диффузионный поток подчиняется уравнению: z закон Фика - градиент концентрации, - коэффициент диффузии.

Знак “ – “ в уравнении объясняется следующим образом. , а . Чтобы , ставят “-”. Найдем коэффициент диффузии. Рассмотрим кубик единичного объема. В нем содержится n одинаковых молекул, которые движутся хаотично. Из рисунка видно, что в каждом из направлений: +x; -x +y; -y +z; -z движется молекул.

Рассчитаем диффузионный поток через поверхность единичной площади, перпендикулярной к направлению потока и проведенной через координату. На интервалах от до и от до поток не меняется, так как на этих интервалах нет столкновений. Тогда поток, пересекающий поверхность при x, равен разности потоков: z , где

Так как - очень маленькая величина, выражения для и можно представить следующим образом:

Из сравнения выражений: находим коэффициент диффузии Зависимость от давления и температуры. при T = const и при p = const

Теплопроводность. Закон Фурье. Если различные части системы имеют разные температуры (газ неравномерно нагрет), то возникает поток тепла от более нагретой части газа к менее нагретой – это явление теплопроводности. В реальных процессах T(t) – нестационарный процесс. Математически легче описать стационарный процесс, когда разность температур не меняется со временем. Рассмотрим газ, заключённый между двумя параллельными стенками, имеющими разную температуру Та и Тб

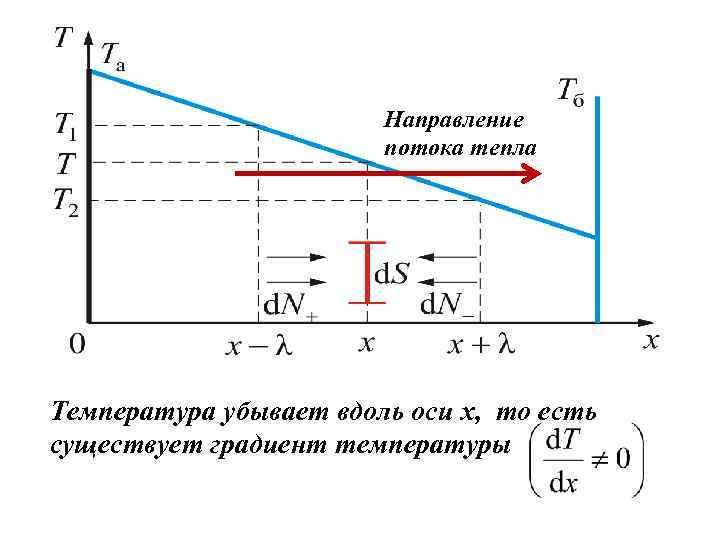Направление потока тепла Температура убывает вдоль оси x, то есть существует градиент температуры

Экспериментально полученный закон Фурье показывает, что поток тепла через единичную площадку, перпендикулярную направлению потока, равен где ( - коэффициент теплопроводности. ). Найдем коэффициент теплопроводности. Рассмотрим поток тепла через площадку единичной площади, расположенную перпендикулярно к направлению потока, за единицу времени.

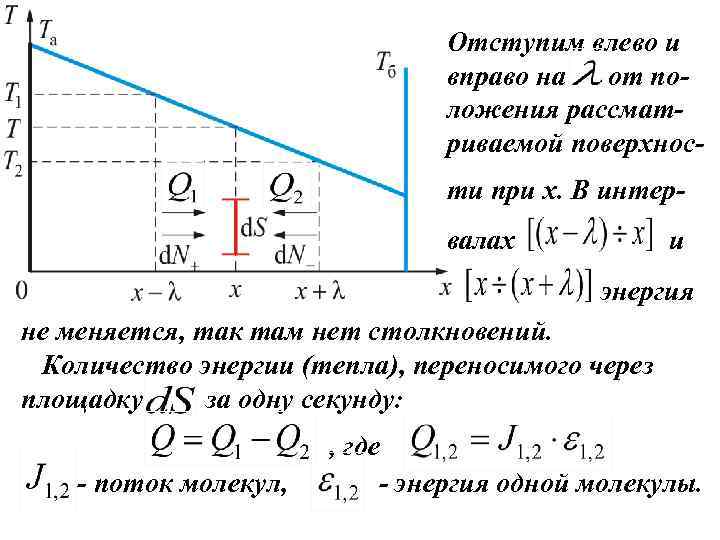Отступим влево и вправо на от положения рассматриваемой поверхности при x. В интервалах и энергия не меняется, так там нет столкновений. Количество энергии (тепла), переносимого через площадку за одну секунду: - поток молекул, , где - энергия одной молекулы.

Энергия одной молекулы

Так как , где - молярная теплоемкость при V=const, а - удельная теплоемкость, то где Тогда - масса одной молекулы.

Окончательно Сравнивая с законом Фурье , получаем выражение для коэффициента теплопроводности

Зависимость Подставим значения от давления и температуры. и Из полученного выражение можно сделать вывод, что не зависит от давления (р). Однако это справедливо, когда. - расстояние между пластинами с разной температурой. Если (термос, сосуд Дьюара), .

Внутреннее трение. Вязкость газов (жидкостей) – это свойство, благодаря которому выравниваются скорости движения различных слоев газа. В природе это приводит к стиханию бурь, смерчей, торнадо. Пусть в покоящемся газе вверх по z, перпендикулярно оси х движется пластинка со скоростью , причём ( – средняя скорость теплового движения молекул). Пластинка увлекает за собой прилегающий слой газа, тот слой – соседний и так далее. Весь газ делится, как бы на тончайшие слои, скользящие вверх тем медленнее, чем дальше они от пластинки. Вторая пластинка неподвижна.

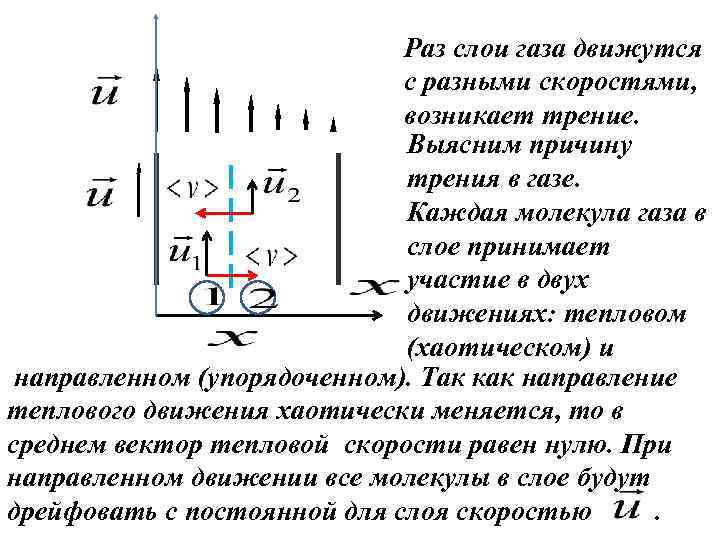Раз слои газа движутся с разными скоростями, возникает трение. Выясним причину трения в газе. Каждая молекула газа в слое принимает участие в двух движениях: тепловом (хаотическом) и направленном (упорядоченном). Так как направление теплового движения хаотически меняется, то в среднем вектор тепловой скорости равен нулю. При направленном движении все молекулы в слое будут дрейфовать с постоянной для слоя скоростью.

Средний импульс отдельной молекулы в слое определяется только дрейфовой скоростью слоя Но так как молекулы участвуют в тепловом движении, они будут переходить из слоя в слой. При этом они будут переносить с собой импульс упорядоченного движения, что будет приводить к изменению импульсов обоих слоев. В примере на рисунке при переходе молекул из слоя 1 в слой 2 суммарный импульс упорядоченного движения слоя 1 уменьшается, а слоя 2 – возрастает, так как. К такому же результату приводит переход молекул из слоя 2 в слой 1.

Обозначим импульс слоя 1 , слоя 2 ное запишем математически: . Сказан- , По 2 -ому закону Ньютона Следовательно, ; . ; и - силы трения между слоями газа, движущимися с разными скоростями. Отсюда и название – внутреннее трение.

Закон вязкости был открыт И. Ньютоном в 1687 г: Импульс, переносимый за 1 с через площадку единичной площади, перпендикулярную направлению переноса , равен: где - коэффициент вязкости - градиент скорости упорядоченного движения Рассчитаем коэффициент вязкости.

Коэффициент вязкости. Импульс одной молекулы Поток импульса упорядоченного движения через единичную площадку за единицу времени:

Так как Коэффициент вязкости

Зависимость от давления и температуры Подставим значения и Из полученного выражение можно сделать вывод, что не зависит от давления (р), но зависит от температуры