Лекция 13 Реальные газы Реальный газ не описывается

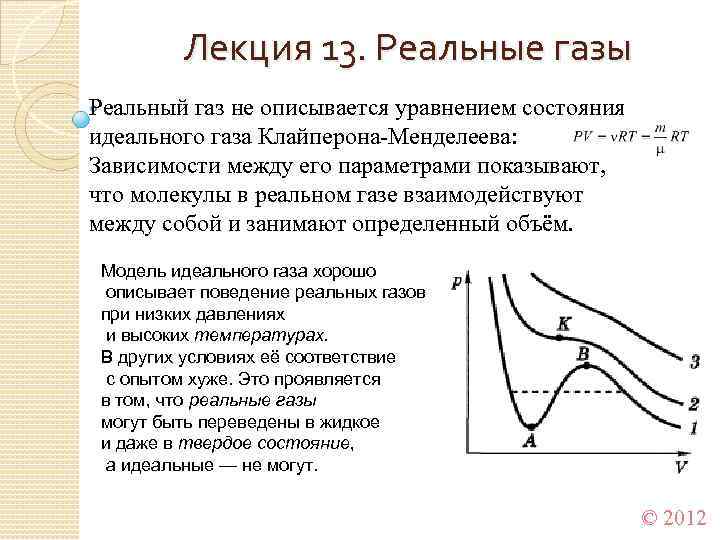Лекция 13. Реальные газы Реальный газ не описывается уравнением состояния идеального газа Клайперона-Менделеева: Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. Модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах. В других условиях её соответствие с опытом хуже. Это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твердое состояние, а идеальные — не могут. © 2012

Реальный газ Модель идеального газа (н. у. ): 1. Не учитывается размер молекул; 2. Не учитывается взаимодействие между молекулами (силы притяжения между молекулами). Повышение давления приводит к уменьшению среднего расстояния между молекулами Нужно учесть собственный объем молекул и сложный характер взаимодействия между ними (поправки Ван-дер-Ваальса) 2

Уравнение Ван-дер-Ваальса Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия становится функцией не только температуры, но и объёма. Для одного моля газа а, b – постоянные Ван-дер-Ваальса, Р – давление, V – молярный объем, Т – абс. тем-ра, R – ун. газ. пост. Имеет компактную форму и учитывает основные характеристики газа с межмолекулярным взаимодействием. 3

Поправки Ван-дер-Ваальса Внутреннее давление: Учитывает взаимодействие между молекулами (силы притяжения) Учитывает собственный объем молекул 4

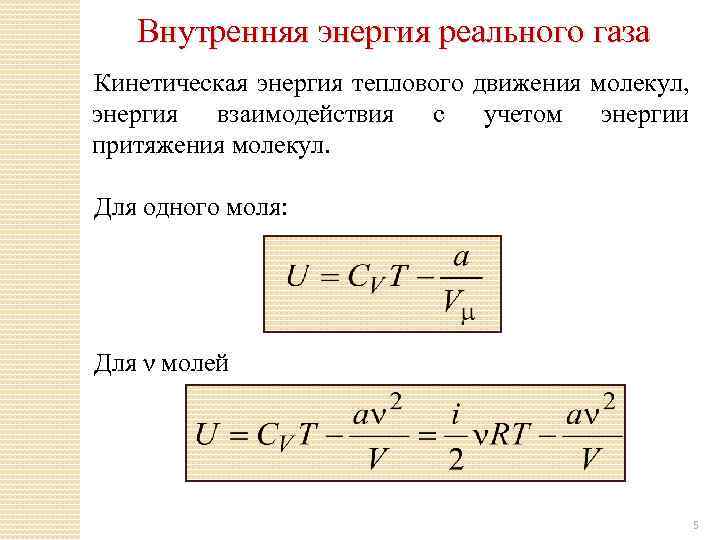Внутренняя энергия реального газа Кинетическая энергия теплового движения молекул, энергия взаимодействия с учетом энергии притяжения молекул. Для одного моля: Для ν молей 5

Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул и из потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ. р΄=а/V 2 Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, идёт на увеличение потенциальной энергии системы. Т. е. d. A=p΄Vm=d. П, или d. П=a/V 2 m*d. Vm, откуда П=-а/Vm. Знак минус означает, что силы ММВ, создающие внутреннее давление р΄, являются силами притяжения. Если газ расширяется без теплообмена со средой и не совершает внешней работы, то на основании 1 начала т. д. получим, что U 1=U 2. Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется. 6

Внутренняя энергия реального газа Использование выражения для внутренней энергии идеального газа позволяет записать формулу, для расчета внутренней энергии газа Ван-дер-Ваальса в виде: Внутренняя энергия газа Ван-дер-Ваальса зависит не только от температуры, как в случае с идеальным газом, но и от его объема. Поэтому при осуществлении изотермических процессов в газе Вандер-Ваальса будет изменяться его внутренняя энергия, и при таких процессах подведенная к газу теплота не будет равна совершенной им работе. Если внутренняя энергия идеального газа определяется кинетической энергией его молекул, то для газа Ван-дер-Ваальса важна потенциальная энергия, обусловленная силами притяжения и отталкивания. Согласно 1 началу т. д. изменение внутренней энергии газа может быть осуществлено либо сообщением ему теплоты, либо совершением над ним механической работы. Если газ адиабатически расширяется, не совершая механической работы, его внутренняя энергия остается неизменной. Для идеального газа неизменность внутренней энергии эквивалентна постоянству температуры газа

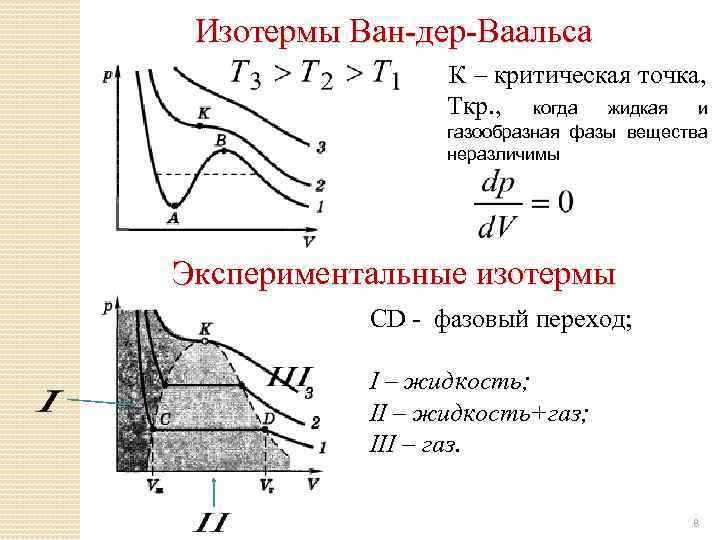Изотермы Ван-дер-Ваальса К – критическая точка, Ткр. , когда жидкая и газообразная фазы вещества неразличимы Экспериментальные изотермы СD - фазовый переход; I – жидкость; II – жидкость+газ; III – газ. 8

Метастабильные состояния Более тщательно проведенный эксперимент: BD – пересыщенный пар, используют в камере Вильсона – установке по наблюдению треков заряженных частиц; При понижении температуры межмолекулярное взаимодействие в реальных газах приводит к конденсации СА – перегретая жидкость, используют в пузырьковой жидководородной камере. 9

Принципиальное значение уравнения Ван-дер-Ваальса 1) уравнение было получено из модельных представлений о свойствах реальных газов и жидкостей, а не явилось результатом эмпирического подбора функции f(p, V, T), описывающей свойства реальных газов; 2) уравнение долго рассматривалось как некоторый общий вид уравнения состояния реальных газов, на основе которого было построено много других уравнений состояния; 3) с помощью уравнения Ван-дер-Ваальса впервые удалось описать явление перехода газа в жидкость и проанализировать критические явления. В этом отношении уравнение Ван-дер-Ваальса имеет преимущество даже перед другими более точными уравнениями

Недостатки уравнения Ван-дер. Ваальса ◦ 1. Для реальных веществ Ккрит более 2, 67 ◦ К крит = РТкрит/p. Vкрит ◦ 2. Для реальных веществ Vкрит = 2 b ◦ 3. Уравнение Ван-дер-Ваальса расходится с экспериментом в области двухфазных состояний.