Лекция 13 Магнитное поле Поле в веществе 1

Лекция 13. Магнитное поле. Поле в веществе 1. 2. 3. 4. 5. 6. 7. 8. Магнитное поле и его характеристики. Закон Био-Саварро-Лапласа. Закон Ампера. Сила Лоренца. Электромагнитная индукция Магнитное поле в веществе. Ферромагнетики. Геомагнитное поле.

1. Магнитное поле и его характеристики В пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. n Оно действует только на движущиеся в этом поле электрические заряды. n

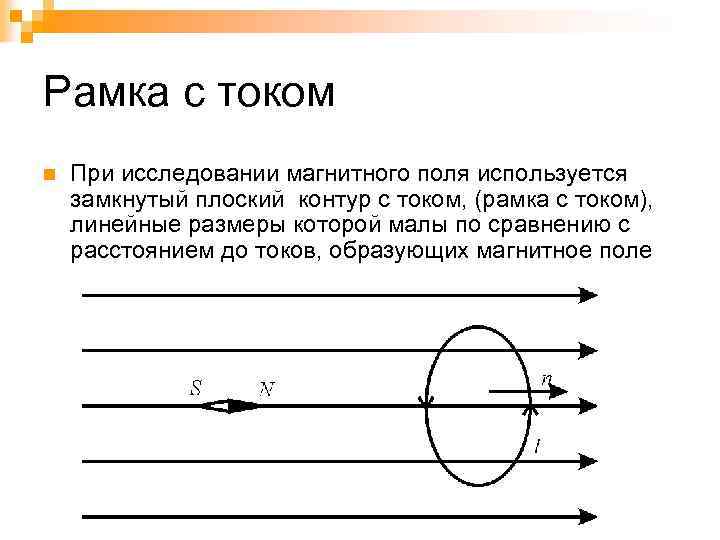Рамка с током n При исследовании магнитного поля используется замкнутый плоский контур с током, (рамка с током), линейные размеры которой малы по сравнению с расстоянием до токов, образующих магнитное поле

Правило правого винта n n Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке

Момент сил Так как в магнитном поле на рамку с током действует пара сил, то она испытывает ориентирующее действие поля. n Вращающий момент сил является векторным произведением n

Магнитная индукция n n вектор магнитного момента рамки с током вектор магнитной индукции Для плоского контура с током Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращательным моментом , действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля

Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции

Принцип суперпозиции n Магнитное поле подчиняется принципу суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций складываемых полей, создаваемых каждым током или движущимся зарядом в отдельности

Магнитное поле в веществе n n Согласно предположению А. Ампера (1775 -1836) существует внешнее магнитное поле и поле в веществе. Внешнее магнитное поле обусловлено действием макротоков. В любом теле также существуют микроскопические круговые токи, создаваемые движением электронов в атомах и молекулах. Магнитное поле макротоков описывается вектором напряжённости

Магнитное поле в веществе n n Вектор магнитной индукции характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряжённости магнитная постоянная безразмерная величина – магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков усиливается за счёт поля микротоков среды.

2. Закон Био-Саварра-Лапласа

Закон Био-Саварра-Лапласа n n Индукция магнитного поля, создаваемого током Сила тока вектор, по модулю равный длине проводника и совпадающий по направлению с током радиус-вектор, проведённый из элемента проводника в точку А поля

Иллюстрация закона Био– Саварра

3. Закон Ампера n n n сила , с которой магнитное поле действует на элемент проводника с током, находящимся в магнитном поле вектор, совпадающий по направлению с током вектор магнитной индукции

Сила Ампера n В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).

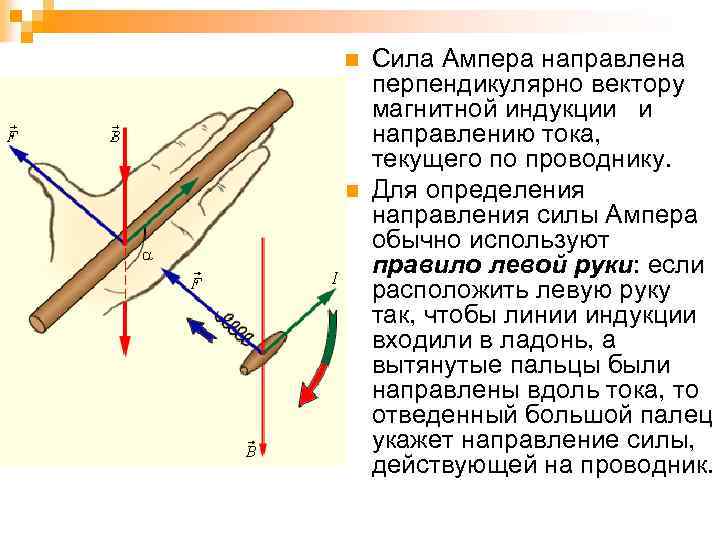n n Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник.

4. Сила Лоренца n n Сила, действующая на электрический заряд , движущийся в магнитном поле со скоростью Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в неё входил вектор , а четыре вытянутых пальца направить вдоль вектора (для направления и совпадают, для они противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд

Сила Лоренца

Взаимное расположение векторов. Модуль силы Лоренца численно равен площади параллелограмма, построенного на векторах и помноженной на заряд q

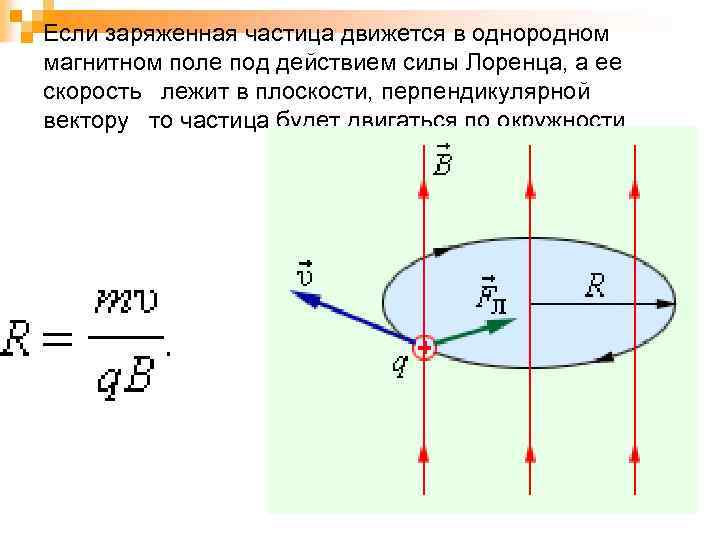Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности

Движение заряженных частиц в вакуумной камере циклотрона

Селектор скоростей и массспектрометр

Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния

5. Электромагнитная индукция n Явление электромагнитной индукции было открыто выдающимся английским физиком М. Фарадеем в 1831 г. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур.

n n Фарадей (Faraday) Майкл (22. IX. 1791– 25. VIII. 1867) Английский физик и химик. Один из основателей количественной электрохимии. Впервые получил (1823) в жидком состоянии хлор, затем сероводород, диоксид углерода, аммиак и диоксид азота. Открыл (1825) бензол, изучил его физические и некоторые химические свойства. Положил начало (1826) исследованиям натурального каучука. Показал возможность фотохимического хлорирования этилена за 15 лет до осуществленного Ж. Б. А. Дюма открытия реакции металепсии. Один из пионеров исследования каталитических реакций. Работал над улучшением качества оптического стекла (1824 – 1830). Получил тяжелое свинцовое стекло, с помощью которого открыл явление магнитного вращения плоскости поляризации. Установил (1833– 1836) количественные законы электролиза. Ввел понятие диэлектрической проницаемости. Имя Фарадея вошло в систему электрических единиц в качестве единицы электрической емкости.

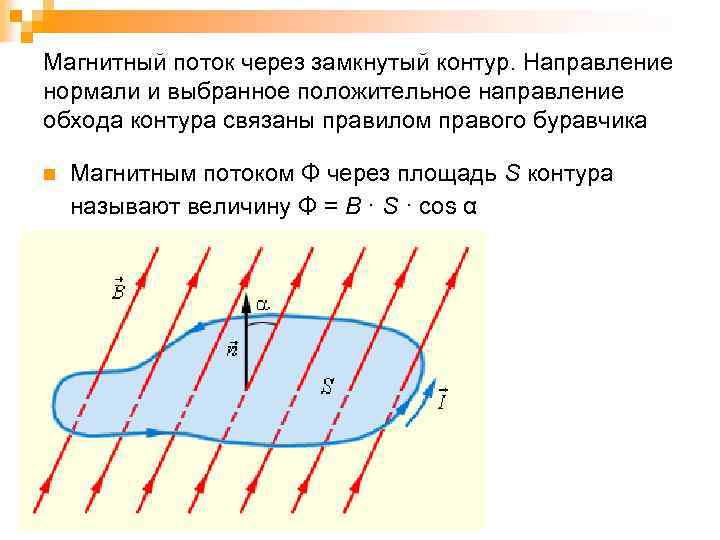Магнитный поток через замкнутый контур. Направление нормали и выбранное положительное направление обхода контура связаны правилом правого буравчика n Магнитным потоком Φ через площадь S контура называют величину Φ = B · S · cos α

Закон Фарадея n Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус

Правило Ленца n Опыт показывает, что индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Иллюстрация правила Ленца. Индукционный ток Iинд течет навстречу выбранному положительному направлению обхода контура

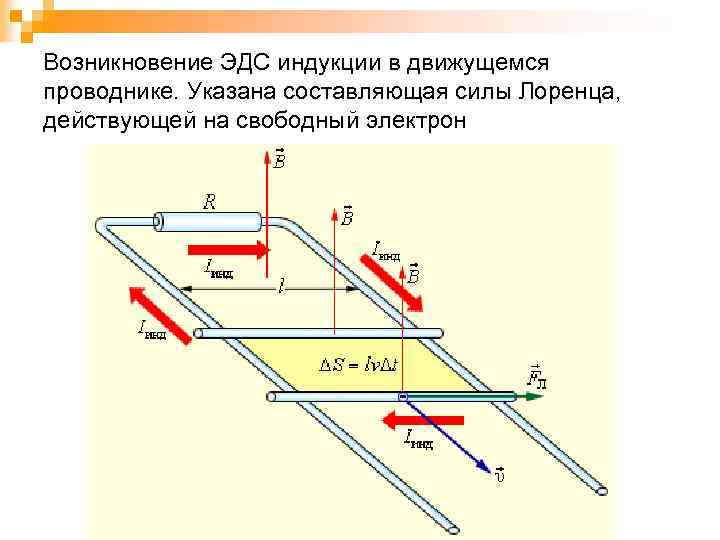Возникновение ЭДС индукции в движущемся проводнике. Указана составляющая силы Лоренца, действующей на свободный электрон

6. Магнитное поле в веществе n n Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Парамагнитные образцы намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю. У парамагнетиков μ > 1 диамагнитные образцы намагничиваются против внешнего поля. У диамагнетиков μ < 1. Отличие μ от единицы у пара- и диамагнетиков чрезвычайно мало.

7. Ферромагнетики n n n Вещества, способные сильно намагничиваться в магнитном поле, называются ферромагнетиками. Магнитная проницаемость ферромагнетиков по порядку величины лежит в пределах 102– 105. Например, у стали μ ≈ 8000, у сплава железа с никелем магнитная проницаемость достигает значений 250000. К рассматриваемой группе относятся четыре химических элемента: железо, никель, кобальт, гадолиний. Из них наибольшей магнитной проницаемостью обладает железо. Поэтому вся эта группа получила название ферромагнетиков.

Свойства ферромагнетиков n n Для каждого ферромагнетика существует определенная температура (так называемая температура или точка Кюри), выше которой ферромагнитные свойства исчезают, и вещество становится парамагнетиком. У железа, например, температура Кюри равна 770 °C, у кобальта 1130 °C, у никеля 360 °C. Ферромагнитные материалы делятся на две большие группы – на магнито-мягкие и магнито-жесткие материалы.

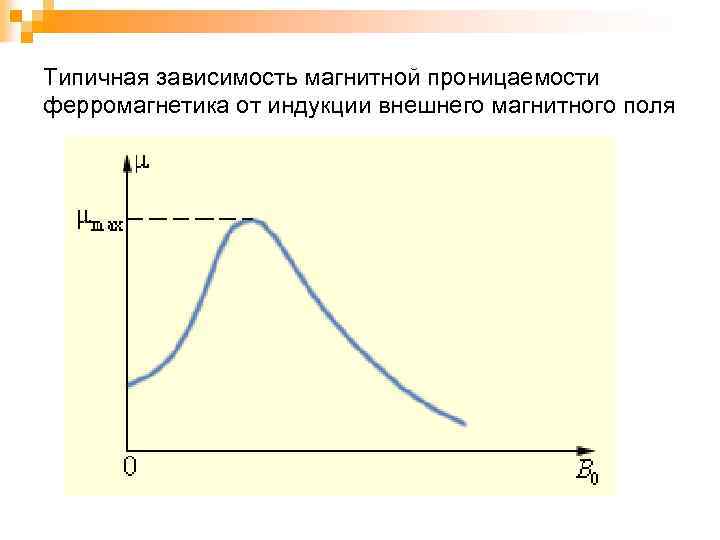Типичная зависимость магнитной проницаемости ферромагнетика от индукции внешнего магнитного поля

Петля гистерезиса ферромагнетика. Стрелками указано направление процессов намагничивания и размагничивания ферромагнитного образца при изменении индукции B 0 внешнего магнитного поля

Намагничивание ферромагнитного образца. (1) B 0 = 0; (2) B 0 = B 01; (3) B 0 = B 02 > B 01

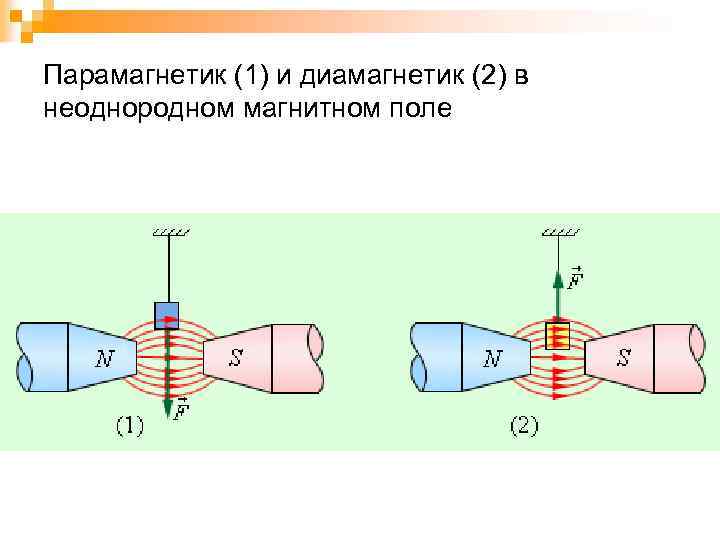Парамагнетик (1) и диамагнетик (2) в неоднородном магнитном поле