Лекция 13 4 ОСНОВЫ ЭЛЕКТРОДИНАМИКИ Движение заряженных частиц

Лекция 13 4. ОСНОВЫ ЭЛЕКТРОДИНАМИКИ Движение заряженных частиц в постоянных электрическом и магнитном полях.

4. 1. Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца. 4. 2. Движение заряженной частицы в однородном постоянном электрическом поле. 4. 3. Движение заряженной частицы в однородном постоянном магнитном поле. 4. 4. Практические применения силы Лоренца. Эффект Холла.

4. 1. Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца. Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику. Этот вывод подтверждается, в частности, еще и тем, что пучок свободно летящих заряженных частиц отклоняется магнитным полем. Сила Ампера, действующая на элемент тока в магнитном поле с индукцией : , где α – угол между направлением тока в проводнике и вектором. Пусть υ – скорость упорядоченного движения зарядов в проводнике; q заряд носителя тока (в металлах q = - e). Для элемента тока можем написать: d. Nqυ, где n = d. N/d. V – концентрация зарядов, d. N – число зарядов в элементе объема d. V = Sdl.

Тогда, сила, действующая в магнитном поле на один заряд, будет: или в векторном виде. Эту силу называют силой Лоренца (Lorentz H. , 1853 -1928). Свойства силы Лоренца: 1. сила Лоренца действует только на движущуюся заряженную частицу; 2. и одновременно ; 3. поскольку , то сила Лоренца не совершает работу, а следовательно, не может изменить энергию частицы. Если помимо магнитного поля присутствует еще и электрическое поле , то на частицу действует дополнительная сила: Полная сила, действующая на заряженную частицу в электромагнитном поле (которую также называют силой Лоренца) есть:

4. 2. Движение заряженной частицы в однородном постоянном электрическом поле. В данном случае составляющую является: и сила Лоренца имеет только электрическую. Уравнением движения частицы в этом случае. Рассмотрим две ситуации: а) и б). а). Изменение кинетической энергии частицы на пути d происходит за счет работы силы : , где U = Ed - ускоряющее напряжение. В частности, если начальная скорость частицы υ0 = 0, то. Время пролета частицы в электрическом поле и пройденный путь находим из уравнений:

б). В данном случае проекции координатные оси дают: уравнения движения частицы на . Координаты частицы в момент времени t составляют: ; . Исключая из этих уравнений параметр t , находим уравнение траектории частицы: Видим, что траекторией движения частицы является парабола. Определим смещение следа частицы на экране, отстоящем от конденсатора на расстоянии b: , где - смещение частицы по вертикали, полученное ею в электрическом поле к моменту вылета из конденсатора ; - смещение частицы после вылета из конденсатора. Таким образом, имеем: .

4. 3. Движение заряженной частицы в однородном постоянном магнитном поле. В данном случае и сила Лоренца имеет только магнитную составляющую. Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является: . Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля. , , и уравнение движения принимает вид: , откуда следует, что вектор полного ускорения частицы лежит в плоскости, перпендикулярной вектору. Легко убедиться также в том, что вектор ускорения перпендикулярен вектору скорости частицы и составляет вместе с вектором правую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно, .

Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен: . Траекторией движения является окружность которой находим из условия: , то есть , радиус R , откуда: . Период обращения частицы Отметим, что период обращения и соответственно угловая скорость движения частицы не зависят от линейной скорости υ.

Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля. Разложим вектор скорости на две составляющие: - параллельную вектору и - перпендикулярную. Поскольку составляющая силы Лоренца в направлении равна нулю, она не может повлиять на величину. Что касается составляющей , то этот случай был рассмотрен выше. Таким образом, движение частицы можно представить как наложение двух движений: одного – равномерного перемещения вдоль направления силовых линий поля со скоростью , второго – равномерного вращения в плоскости, перпендикулярной. В итоге траекторией движения будет винтовая линия. Шаг винтовой линии определяется по формуле: , где. Радиус витка находим по формуле: Направление, в котором закручивается винтовая линия, зависит от знака заряда частицы. Если заряд частицы положительный, то винтовая линия закручивается против часовой стрелки, если смотреть вдоль направления , и наоборот – по часовой стрелке, если заряд частицы отрицательный.

4. 4. Практические применения силы Лоренца. Эффект Холла. К числу одного из известных проявлений силы Лоренца относится эффект, обнаруженный Холлом (Hall E. , 1855 -1938) в 1880 г. Суть явления заключается в следующем: если металлическую пластинку, вдоль которой течет постоянный ток, поместить в магнитное поле, то между параллельными току и полю гранями пластинки возникает разность потенциалов, величина которой определяется выражением: , где b – толщина пластинки; j - плотность тока; R – так называемая постоянная Холла.

Эффект Холла объясняется действием силы Лоренца на движущиеся в металле электроны, создающие ток. Направление тока противоположно направлению движения электронов. Поэтому при включении магнитного поля на каждый электрон будет действовать сила, направленная к нижней грани пластинки и равная по величине. В результате на нижней грани появятся избыточные отрицательные заряды, а на верхней - соответственно избыточные положительные заряды. Между верхней и нижней гранью возникнет разность потенциалов U, то есть электрическое поле. Напряженность поля. Сила, действующая на электрон со стороны этого поля, направлена вверх и равна по величине: . При установившемся процессе разделения зарядов , откуда, принимая во внимание, что плотность тока , находим холловскую разность потенциалов: Постоянная Холла , где n – концентрация электронов в металле. Эффект Холла наблюдается не только в металлах, но и в полупроводниках, а также в электролитах. Знак холловской разности потенциалов зависит от знака носителя заряда. Поэтому эффект Холла широко применяют не только для определения концентрации носителей заряда в полупроводниках, но также для определения типа полупроводника.

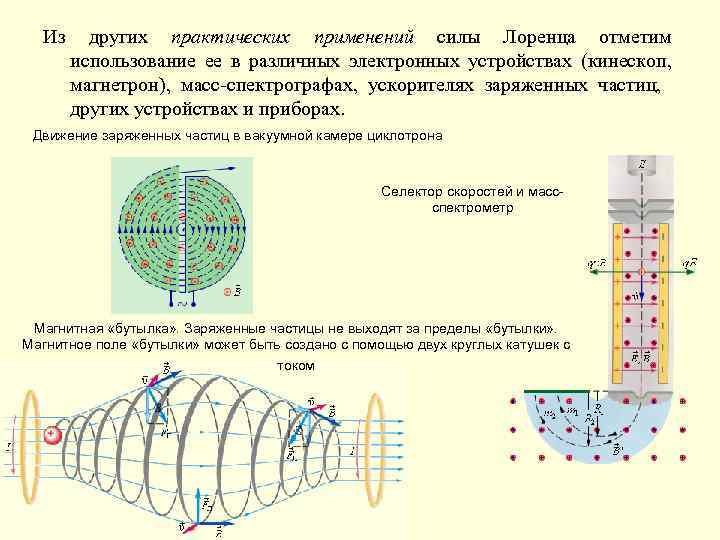Из других практических применений силы Лоренца отметим использование ее в различных электронных устройствах (кинескоп, магнетрон), масс-спектрографах, ускорителях заряженных частиц, других устройствах и приборах. Движение заряженных частиц в вакуумной камере циклотрона Селектор скоростей и массспектрометр Магнитная «бутылка» . Заряженные частицы не выходят за пределы «бутылки» . Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током

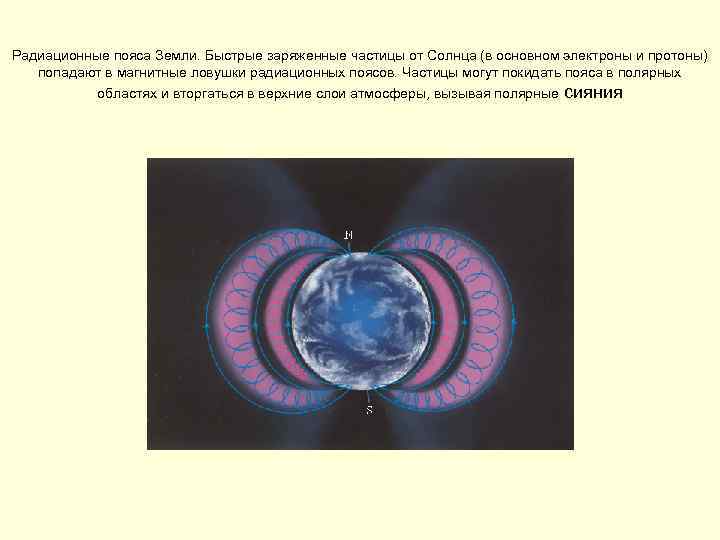Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния