ЛЕКЦИЯ 12 ВОПРОСЫ К ЭКЗАМЕНУ Для студентов

ЛЕКЦИЯ 12

ВОПРОСЫ К ЭКЗАМЕНУ Для студентов 2 курса 1 семестр 2016 -17 уч. г. 1. Магнитное поле. Магнитная индукция. Закон Био-Савара-Лапласа. 2. Закон Ампера. Взаимодействие параллельных токов. Магнитная постоянная. 3. Магнитное поле движущегося заряда. Сила Лоренца. Движение заряда в магнитном поле. 4. Циркуляция вектора магнитной индукции. Магнитный момент кругового тока. 5. Магнитное поле тороида и соленоида. Энергия магнитного поля соленоида 6. Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля. 7. Работа по перемещению проводника и контура в магнитном поле. 8. Электромагнитная индукция. Правило Ленца. Закон Фарадея. 9. Индуктивность. Самоиндукция. Токи при замыкании и размыкании цепи. 10. Взаимная индукция. Трансформаторы. 11. Энергия магнитного поля. Объемная плотность энергии магнитного поля. 12. Магнитные моменты атомов и электронов. Диа- и парамагнетики. 13. Намагниченность. Закон полного тока для магнитного поля в веществе. 14. Ферромагнетики. Магнитный гистерезис. 15. Магнитное поле на границе двух сред. 16. Основы теории Максвелла для электромагнитного поля. 17. Гармонические колебания и их характеристики. Дифференциальное уравнение. Скорость, ускорение, энергия механических гармонических колебаний. 18. Гармонический осциллятор. Пружинный, математический и физический маятники. 19. Сложение гармонических колебаний сонаправленных и перпендикулярных. Биения. 20. Свободные затухающие колебания. 21. Свободные гармонические и затухающие колебания в колебательном контуре.

22. Вынужденные колебания. Резонанс 23. Волны. Виды волн. Гармонические волны. 24. Принцип суперпозиции. Групповая скорость. Стоячие волны. 25. Законы оптики. Основные фотометрические единицы. 26. Геометрическая оптика. Линзы. Волновая и корпускулярная теории природы света 27. Интерференция света. Монохроматичность. Когерентность света. 28. Интерференция света в тонких пленках. Кольца Ньютона. Применение интерференции. 29. Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. 30. Прямолинейное распространение света. Дифракция Френеля на круглом отверстии и диске. 31. . Дифракция Фраунгофера на узкой щели и дифракционной решетке 32. Дифракция на пространственной решетке. Формула Вульфа-Брэгга. Разрешающая способность приборов. 33. Поляризация света. Естественный и поляризованный свет. Закон Малюса. Поляризация на границе двух диэлектриков. 34. Двойное лучепреломление. Интерференция поляризованного света Искусственная оптическая анизотропия Вращение плоскости поляризации. 35. Квантовая природа излучения. Тепловое излучение. Черное и серое тела Закон Кирхгофа. 36. Закон Стефана-Больцмана. Закон смещения Вина. Формулы Рэлея-Джинса и Планка. 37. Квантовая гипотеза. Оптическая пирометрия 38. Внешний фотоэффект и его законы. Фотоны. Уравнение Эйнштейна для внешнего фотоэффекта. 39. Эффект Комптона и его теория. Давление света. Корпускулярно волновая двойственность света. 40. Ядерные модели Томпсона и Резерфорда. Линейчатый спектр излучения атома водорода.

41. Корпускулярно волновой дуализм свойств вещества. Формула де Бройля. Волны де Бройля. 42. Соотношение неопределенностей Гейзенберга. 43. Волновая функция и её статистический смысл. 44. Уравнение Шредингера. 45. Теория Бора для водородоподобных систем Постулаты Бора. 46. Движение свободной частицы. Частица в одномерной потенциальной яме. 47. Водородоподобная система в квантовой механике. Энергетические уровни. Основное состояние атома водорода. Спин электрона 48. Принцип неразличимости тождественных частиц. Фермионы и бозоны. Принцип Паули. 49. Периодическая система элементов Менделеева. Молекулы. Энергетические уровни молекул. Поглощение, спонтанное и вынужденное излучения фотонов. 50. Ядро атома. Модели ядра. Ядерные силы. Дефект массы и энергия связи ядра. 51. Радиоактивное излучение. Законы радиоактивного распада. 52. Ядерные реакции. Общая классификация ядерных реакций. Цепная реакция деления.

КВАНТОВАЯ ПРИРОДА ИЗЛУЧЕНИЯ

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ

ХАРАКТЕРИСТИКИ ТЕПЛОВОГО ИЗЛУЧЕНИЯ

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ Нагретые до достаточно высоких температур тела светятся. Свечение обусловлено ТЕМПЕРАТУРНЫМ ТЕПЛОВЫМ ИЗЛУЧЕНИЕМ. Данное излучение является самым распространенным в природе, совершается за счет теплового движения атомов и молекул вещества, (то есть за счет внутренней энергии), и свойственно всем телам при температуре выше 0 К. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких в основном длинные (инфракрасные). Тепловое излучение единственный вид излучения которое может быть РАВНОВЕСНЫМ , (то есть при определенных условиях тело в единицу времени может поглощать столько же энергии, сколько и излучать)

Если равновесие между телом и излучением по какой то причине нарушено , и тело излучает больше энергии чем поглощает , (или наоборот), то, со временем, температура тела будет понижаться (или, соответственно, повышаться). В результате будет уменьшаться (при нагревании возрастать) количество излучаемой телом энергии, пока не установится равновесие. Все другие виды излучения, кроме теплового, НЕРАВНОВЕСНЫЕ.

ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА Количественной характеристикой теплового излучения служит СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ СВЕТИМОСТИ (ИЗЛУЧАТЕЛЬНОСТЬ) ТЕЛА. ИЗЛУЧАТЕЛЬНОСТЬ ТЕЛА – мощность излучения с единицы площади поверхности тела, в интервале частот единичной ширины. – энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения), с единицы площади поверхности тела, в интервале частот от до. Единица измерения излучательности тела:

Записанную формулу можно представить в виде функции длины волны: Так как , то Знак минус показывает на то, что с ростом одной из величин ( или ) другая будет убывать. Поэтому, в даль -нейшем знак минус можно опускать. Значит : Зная спектральную плотность энергетической светимости можно определить интегральную энергетическую светимость (интегральную излучательность) или энергетическую светимость тела:

СПЕКТРАЛЬНАЯ ПОГЛОЩАТЕЛЬНАЯ СПОСОБНОСТЬ Способность тел поглощать падающее на них излучение характеризуется: СПЕКТРАЛЬНОЙ ПОГЛОЩАЮЩЕЙ СПОСОБНОСТЬЮ : Спектральная поглощающая способность показывает какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на неё электромагнитными волнами с частотами от до поглощается телом. – величина безразмерная. и зависят от природы тела, его температуры, и, при этом различаются для излучений с различными

частотами. Поэтому эти величины относят к определенным температурам и частотам (точнее к максимально узкому интервалу частот от до ).

АБСОЛЮТНО ЧЕРНОЕ ТЕЛО Тело, способное поглощать полностью, при любой температуре всё падающее на него излучение называется: АБСОЛЮТНО ЧЕРНЫМ ТЕЛОМ. Спектральная поглощательная способность черного тела для всех частот и температур равна единице: . Абсолютно черных тел в природе нет, но существуют тела по своим свойствам достаточно близкие к ним. Хорошей моделью черного тела является замкнутая полость, внутренняя поверхность которой зачернена. Луч • света попавший внутрь неё испытывает многократные отражения от стенок, в результате интенсивность вышедшего луча будет близка к нулевой.

СЕРОЕ ТЕЛО – тело, поглощательная способность которого меньше единицы, но одинаково для всех частот и зависит только от температуры, материала и состояния поверхности тела. Рассмотрим законы, которым подчиняется тепловое излучение.

ЗАКОН КИРХГОФА

Опираясь на второе начало термодинамики, и анализизруя условия равновесного излучения Кирхгоф установил количественную связь между спектральной плотностью энергетической светимости и спектральной поглощательной способностью тел. Отношение спектральной плотности энергетической светимости к спектральной поглощательной способности НЕ ЗАВИСИТ от природы тела, оно является для всех тел универсальной функцией частоты (длины волны) и температуры. Так как для абсолютно черного тела то получается

СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ ЭНЕРГЕТИЧЕСКОЙ СВЕТИМОСТИ ЧЕРНОГО ТЕЛА – УНИВЕРСАЛЬНАЯ ФУНКЦИЯ КИРХГОФА или спектральная плотность энергетической светимости черного тела. По закону Кирхгофа для всех тел отношение к равно спектральной плотности энергетической светимости черного тела при той же температуре и частоте. Выражению энергетической светимости тела можно придать вид: Для серого тела: – энергетическая светимость черного тела

Из закона Кирхгофа следует что: 1. любого тела, в любой области спектра, всегда меньше (при тех же значениях и ). Так как то. 2. Если тело не поглощает электромагнитной волн какой либо частоты, то оно их и не излучает, так как при будет. Закон Кирхгофа описывает только тепловое излучение. Излучение которое не подчиняется закону Кирхгофа не является тепловым.

ЗАКОН СТЕФАНА-БОЛЬЦМАНА. ЗАКОН СМЕЩЕНИЯ ВИНА

ЗАКОН СТЕФАНА-БОЛЬЦМАНА Спектральная плотность энергетической светимости черного тела является универсальной функцией, и нахождение её явной зависимости от частоты (длины волны) и температуры является важной задачей теории теплового излучения. Й. Стефан анализируя экспериментальные данные (1879) и Л. Больцман применяя термодинамический метод (18840 установили зависимость энергетической светимости от температуры: Энергетическая светимость черного тела пропорциональна четвертой степени его термодинамической температуры.

– постоянная Стефана-Больцмана Для серого тела закон Стефана-Больцмана имеет вид: – энергетическая светимость серого тела – коэффициент теплового излучения серого тела

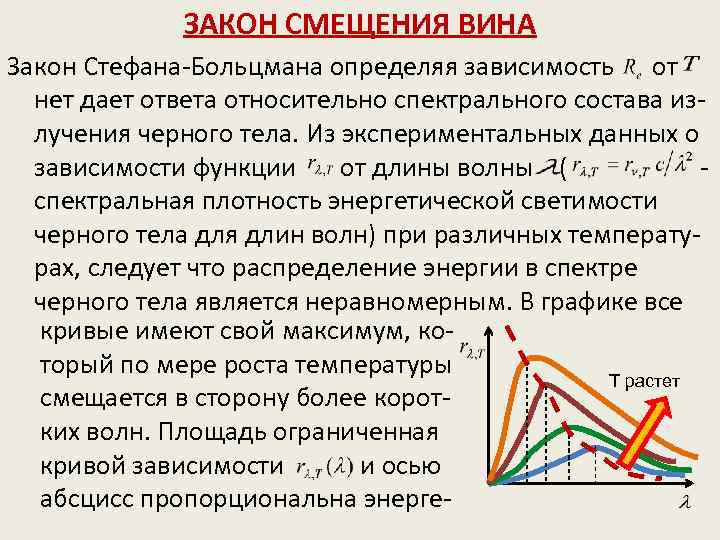ЗАКОН СМЕЩЕНИЯ ВИНА Закон Стефана-Больцмана определяя зависимость от нет дает ответа относительно спектрального состава излучения черного тела. Из экспериментальных данных о зависимости функции от длины волны ( спектральная плотность энергетической светимости черного тела для длин волн) при различных температурах, следует что распределение энергии в спектре черного тела является неравномерным. В графике все кривые имеют свой максимум, который по мере роста температуры Т растет смещается в сторону более коротких волн. Площадь ограниченная кривой зависимости и осью абсцисс пропорциональна энерге-

тической светимости черного тела, и , по закону Стефана-Больцмана четвертой степени температуры. В. Вин установил зависимость длины волны , соответствующей максимуму функции от температуры Т. ЗАКОН СМЕЩЕНИЯ ВИНА: Длина волны соответствующая максимальной плотности энергетической светимости черного тела, обратно пропорциональна его термодинамической температуре. – постоянная Вина

Закон смещения Вина показывает смещение положения максимума функции по мере возрастания температуры в области коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел цвет переходит от белого к красному. Законы Стефана-Больцмана и Вина – частные законы, которые не дают общей картины распределения энергии по частотам при разных температурах.

ФОРМУЛА РЭЛЕЯ-ДЖИНСА. ФОРМУЛА ПЛАНКА. КВАНТЫ

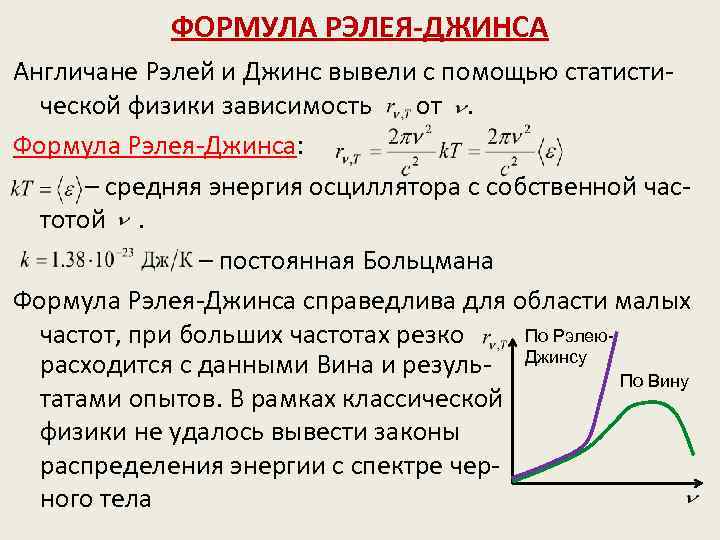ФОРМУЛА РЭЛЕЯ-ДЖИНСА Англичане Рэлей и Джинс вывели с помощью статистической физики зависимость от. Формула Рэлея-Джинса: – средняя энергия осциллятора с собственной частотой. – постоянная Больцмана Формула Рэлея-Джинса справедлива для области малых По Рэлеючастот, при больших частотах резко расходится с данными Вина и резуль- Джинсу По Вину татами опытов. В рамках классической физики не удалось вывести законы распределения энергии с спектре черного тела

КВАНТОВАЯ ГИПОТЕЗА. ФОРМУЛА ПЛАНКА Правильное, соответствующее с опытными данными, выражение для спектральной плотности энергетической светимости было найдено в 1900 г. Планком. Планк отказался от мысли что энергия любой системы может изменятся непрерывно, то есть принимать какие угодно значения. Согласно КВАНТОВОЙ ГИПОТЕЗЕ: Атомные осцилляторы излучают энергию не непрерывно а определенными порциями– КВАНТАМИ , причем, энергия кванта пропорциональна частоте колебания: – энергия кванта – постоянная Планка

Так ка излучение испускается порциями, то энергия осциллятора дискретна и кратна целому числу элементарных значений энергии. Средняя энергия осциллятора: Спектральная плотность энергетической светимости черного тела:

Планк вывел формулу для универсальной функции Кирхгофа: Данная формула согласуется с экспериментальными данными по распределению энергий в спектрах излучения черного тела, во всем интервале частот и температур. Из формулы Планка можно вывести закон Рэлея-Джинса для области малых частот, закон Стефана-Больцмана и закон сохранения Вина. Зная универсальные постоянные можно вывести постоянные Стефана-Больцмана , Вина , и наоборот. Формула Планка не только хорошо согласуется с экспериментальными данными, но и содержит в себе частные законы теплового излучения, то есть является полным решением основной задачи теплового излучения поставленной Планком.

ОПТИЧЕСКАЯ ПИРОМЕТРИЯ. ТЕПЛОВЫЕ ИСТОЧНИКИ СВЕТА

ОПТИЧЕСКАЯ ПИРОМЕТРИЯ Законы теплового излучения используются для измерения температуры раскаленных и недоступных для контактного измерения температуры тел. Методы измерения высоких температур, использующие зависимость спектральной плотности энергетической светимости тел от температуры называются ОПТИЧЕСКОЙ ПИРОМЕТРИЕЙ. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения называются – пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел различают: радиационную, цветовую и яркостную температуры.

РАДИАЦИОННАЯ ТЕМПЕРАТУРА – такая температура черного тела, при котором его энергетическая светимость равна энергетической светимости исследуемого тела. В этом случае регистрируется энергетическая све-тимость исследуемого тела и по закону Стефана-Больц-мана вычисляется его радиационная температура. Радиационная температура тела всегда меньше его истинной температуры. Для доказательства этого предположим что исследуемое тело является серым. Тогда можно представить что: Так как истинная температура всегда выше

ЦВЕТОВАЯ ТЕМПЕРАТУРА Для серых тел спектральная плотность энергетической светимости где. Значит распределение энергии в спектре излучения серого тела такое же, как и в спектре черного тела имеющего ту же температуру. Поэтому к серым телам применим закон Вина, то есть, зная длину волны соответствующую максимальной спектральной плотности энергетической светимости исследуемого тела, можно определить его температуру, которая называется ЦВЕТОВОЙ ТЕМПЕРАТУРОЙ: . Для серых тел цветовая температура совпадает с истинной, а для тех тел, которые сильно отличаются от серых понятие цветовой температуры теряет смысл.

ЯРКОСТНАЯ ТЕМПЕРАТУРА – температура черного тела, при которой для определенной длины волны, его спек-тральная плотность энергетической светимости равна спектральной плотности энергетической светимости исследуемого тела. То есть ( – истинная тем-пература тела). По закону Кирхгофа, для исследуемого тела при длине волны : следовательно: Так как для нечерных тел , то , и значит то есть истинная температура больше яркостной. ,

В качестве яркостного пирометра обычно используется пирометр с исчезающей нитью накала. Нить накала подбирается так, что бы выполнялось условие. В этом случае изображение нити пирометра становится неразличимым на фоне поверхности раскаленного тела, и нить «исчезает» . Используя проградуированный по черному телу миллиамперметр, можно определить яркостную температуру. Зная поглощательную способность тела при той же самой длине волны, по яркостной температуре можно определить истинную. Переписав формулу Планка в виде:

и учитывая что получим: При известных и можно определить температуру исследуемого тела.

ФОТОЭФФЕКТ

ВИДЫ ФОТОЭЛЕКТРИЧЕСКОГО ЭФФЕКТА. ЗАКОНЫ ВНЕШНЕГО ФОТОЭФФЕКТА

ВИДЫ ФОТОЭЛЕКТРИЧЕСКОГО ЭФФЕКТА Гипотеза Планка, решавшая задачу теплового излучения черного тела, получила подтверждение и развитие при объяснении ФОТОЭЛЕКТРИЧЕСКОГО ЭФФЕКТА (ФОТОЭФФЕКТА). Существуют три вида фотоэффекта: • Внутренний фотоэффект • Внешний фотоэффект • Вентильный фотоэффект

ВНУТРЕННИЙ ФОТОЭФФЕКТ – вызванные электромагнитным излучением переходы электронов внутри полупроводника или диэлектрика из связанных состояний в свободные без вылета наружу. Концентрация носителей тока внутри вещества увеличивается, что приводит к возникновению фотопроводимости ( повышению электропроводности вещества при его освещении, или к возникновению электродвижущей силы (ЭДС).

ВЕНТИЛЬНЫЙ ФОТОЭФФЕКТ – является разновидностью внутреннего фотоэффекта, - возникновение ЭДС (фото-ЭДС) прои освещении контакта двух разных полупроводников или полупроводника и металла (при отсутствии внешнего электрического поля). Вентильный эффект открывает пути для прямого преобразования световой энергии в электрическую.

ВНЕШНИЙ ФОТОЭФФЕКТ ВНЕШНИЙ ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ (ФОТОЭФФЕКТ) – испускание электрона веществом под действием электромагнитного излучения. Внешний фотоэффект наблюдается в твердых телах (металлах, полупроводниках, диэлектриках), а, так же в газах на отдельных атомах и молекулах (фотоионизация). Внешний фотоэффект был обнаружен в 1887 г. Г. Герцем, наблюдавшим усиление процесса разряда при облучении искрового промежутка ультрафиолетовым излучением. γ е

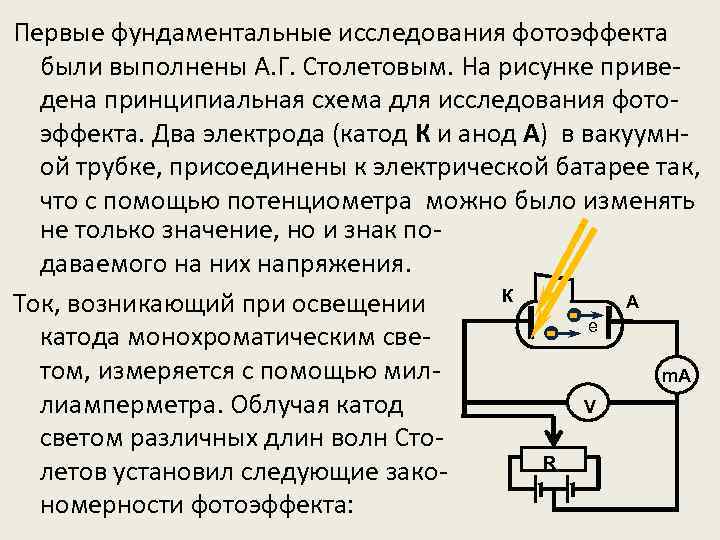Первые фундаментальные исследования фотоэффекта были выполнены А. Г. Столетовым. На рисунке приведена принципиальная схема для исследования фотоэффекта. Два электрода (катод К и анод А) в вакуумной трубке, присоединены к электрической батарее так, что с помощью потенциометра можно было изменять не только значение, но и знак подаваемого на них напряжения. К А Ток, возникающий при освещении e катода монохроматическим светом, измеряется с помощью милm. A лиамперметра. Облучая катод V светом различных длин волн Сто. R летов установил следующие закономерности фотоэффекта:

ЗАКОНОМЕРНОСТИ СТОЛЕТОВА 1. Наиболее эффективное воздействие оказывает ультрафиолетовое излучение. 2. Под действием света вещество теряет только отрицательные заряды. 3. Сила тока, возникающая под действием света, прямо пропорциональна его интенсивности. Томпсон в 1898 году измерил удельный заряд испускаемых под действием света частиц (по отклонению в электрических и магнитных полях). Данные измерения показали, что под действием света вырываются электроны.

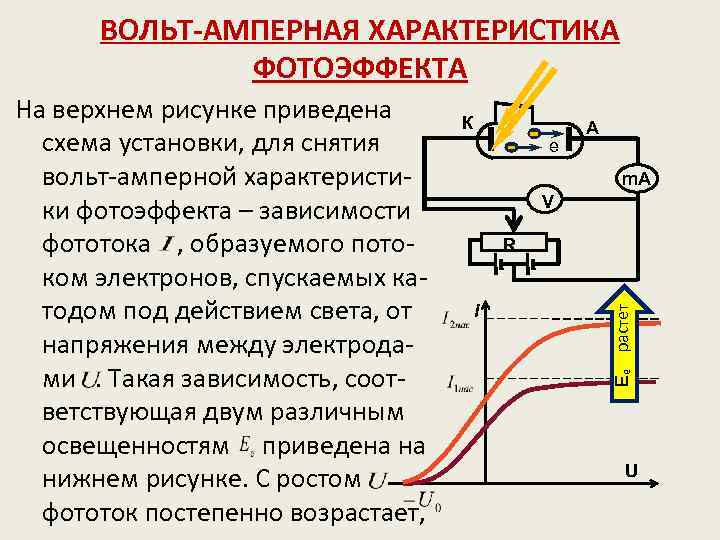ВОЛЬТ-АМПЕРНАЯ ХАРАКТЕРИСТИКА ФОТОЭФФЕКТА К e А m. A V R I Eₑ растет На верхнем рисунке приведена схема установки, для снятия вольт-амперной характеристики фотоэффекта – зависимости фототока , образуемого потоком электронов, спускаемых катодом под действием света, от напряжения между электродами. Такая зависимость, соответствующая двум различным освещенностям приведена на нижнем рисунке. С ростом фототок постепенно возрастает, U

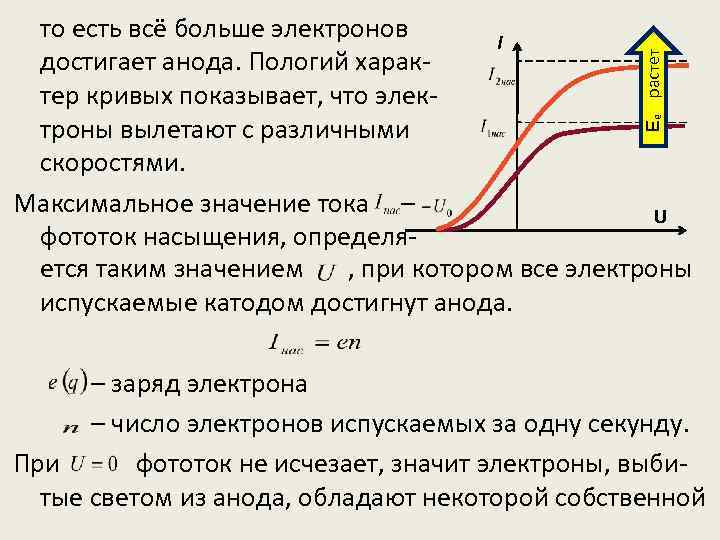Eₑ растет то есть всё больше электронов I достигает анода. Пологий характер кривых показывает, что электроны вылетают с различными скоростями. Максимальное значение тока – U фототок насыщения, определяется таким значением , при котором все электроны испускаемые катодом достигнут анода. – заряд электрона – число электронов испускаемых за одну секунду. При фототок не исчезает, значит электроны, выбитые светом из анода, обладают некоторой собственной

начальной скоростью, а значит и кинетической энергией, и могут достигнуть анода без внешнего поля. Для того что бы фототок стал равным нулю, необходимо приложить задерживающее напряжение. При ни один из электронов, даже обладающий при вылете максимальной скоростью , не может преодолеть задерживающего поля и достигнуть анода, значит: Измерив задерживающее напряжение , можно определить максимальные значения скорости и кинетической энергии фотоэлектронов. При изучении вольт-амперных характеристик различных материалов были выведены следующие три закона фотоэффекта:

ТРИ ЗАКОНА ВНЕШНЕГО ФОТОЭФФЕКТА 1. (закон Столетова) При фиксированной частоте падающего света число фотоэлектронов вырываемых из катода в единицу времени, пропорционально энергетической освещенности катода. 2. Максимальная начальная скорость (кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой. 3. Для каждого вещества существует КРАСНАЯ ГРАНИЦА ФОТОЭФФЕКТА – минимальная частота света ( зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.

УРАВНЕНИЕ ЭЙНШТЕЙНА ДЛЯ ВНЕШНЕГО ФОТОЭФФЕКТА

В 1905 году А. Эйнштейн показал, что явление фотоэффекта и его закономерности могут быть объяснены с помощью КВАНТОВОЙ ТЕОРИИ ФОТОЭФФЕКТА: Свет частотой не только испускается, но и распространяется в пространстве, и поглощается веществом отдельными порциями (КВАНТАМИ), энергия которых: Свет можно рассматривать не как непрерывный волновой процесс, а как поток дискретных световых квантов, двигающихся со скоростью света. Кванты электромагнитного излучения называются: ФОТОНЫ. Каждый фотон поглощается только одним электроном. Значит, число вырванных фотоэлектронов пропорцио-

ционально интенсивности света (1 закон). Безинерционность фотоэффекта объясняется тем, что передача энергии при столкновении фотона с электроном происходит почти мгновенно. Энергия падающего фотона расходуется на совершение электроном работы выхода из металла , и на сообщение вырванному электрону кинетической энергии. УРАВНЕНИЕ ЭЙНШТЕЙНА ДЛЯ ВНЕШНЕГО ФОТОЭФФЕКТА Уравнение Эйнштейна для внешнего фотоэффекта позволяет объяснить 2 и 3 законы фотоэффекта. Так как (для данного вещества), то максимальная кинетическая энергия электрона, растет

с ростом частоты падающего излучения, и не зависит от интенсивности (числа фотонов) (2 закон), и наоборот, при уменьшении частоты света, энергия уменьшазется, и при достижении достаточно малой частоты света , кинетическая энергия станет равной нулю и фотоэффект прекратится. (3 закон). – красная граница фотоэффекта для данного металла. Зависит только от работы выхода электрона, то есть от химической природы вещества. Иная форма записи уравнения Эйнштейна для внешнего фотоэффекта.

Если интенсивность света очень велика(лазерные пучки), то возможен многофотонный (нелинейный) фотоэффект, при котором электрон испускаемый металлом может получить энергию не от одного а от нескольких фотонов. При этом электрон может приобрести энергию, необходимую для выхода из вещества, даже под действием света с частотой меньшей красной границы – порога однофотонного фотоэффекта. В результате красная граница смещается в сторону более длинных волн.

МАССА И ИМПУЛЬС ФОТОНА. ДАВЛЕНИЕ СВЕТА

МАССА ФОТОНА Свет испускается, распространяется и поглощается фотонами. Энергия фотона: . Масса фотона находится из закона взаимосвязи массы и энергии: Фотон – элементарная частица, которая всегда (в любой среде) движется со скоростью света и имеет массу покоя равную нулю. Масса фотона отличается от массы таких элементарных частиц как электроны, протоны и т. д. , которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.

ИМПУЛЬС ФОТОНА Импульс фотона можно получить, если в общей формуле теории относительности приложить массу покоя фотона : Из приведенных рассуждений следует, что фотон, как и любая другая частица, характеризуется массой , энергией и импульсом. Формулы для вычисления этих величин связывают корпускулярные характеристики фотона (энергию, массу и импульс) с волновыми (частотой и длиной волны).

ДАВЛЕНИЕ ФОТОНА Если фотон обладает импульсом, то свет попадающий на тело должен оказывать на него давление. Согласно квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передаёт ей свой импульс. Пусть поток монохроматического излучения (частотой ) падает перпендикулярно поверхности. В единицу времени на единицу площади поверхности тела падает фотонов, то при коэффициенте отражения света от поверхности отразится фотонов, а поглотится. Каждый поглощенный фотон передает поверхности импульс , а каждый отраженный (при отражении импульс фотона меняется на ).

Давление света на поверхность равно импульсу, который передают поверхности за время равное 1 с фотонов. – энергия всех фотонов, падающих на единицу поверхности в единицу времени, то есть энергетическая освещенность поверхности – объемная плотность энергии излучения Давление производимое светом при нормальном падении на поверхность. Давление света одинаково успешно объясняется и волновой и квантовой теорией. Теоретические формулы были подтверждены исследованиями.

ЭФФЕКТ КОМПТОНА И ЕГО ЭЛЕМЕНТАРНАЯ ТЕОРИЯ

Наиболее полно корпускулярные свойства света проявляются в ЭФФЕКТЕ КОМПТОНА. А. Комптон (1892 -1962) исследуя в 1923 г. рассеяние монохроматического рентгеновского излучения веществами с легкими атомами, обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается так же более коротко-волновое излучение. Опыты показали, что разность не зависит от длины волны падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния. Эффект Комптона не укладывается в рамки волновой теории (длина волны при рассеянии изменяться не должна), но объясняется с точки зрения квантовой теории. Он является результатом упругого столкновения рентгеновских фотонов со свободными электронами, при котором фотон передает электрону часть своих энергии и импульса в соответствии с законом сохранения.

ЭФФЕКТ КОМПТОНА – упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского и γ -излучений) на свободных (или слабосвязанных) электронах вещества, сопровождающееся увеличением длины волны. – длина волны падающего излучения – длина волны рассеянного излучения – комптоновская длина волны (при рассеянии на электроне ) – угол рассеяния – разность рассеянной и падающей длин волн

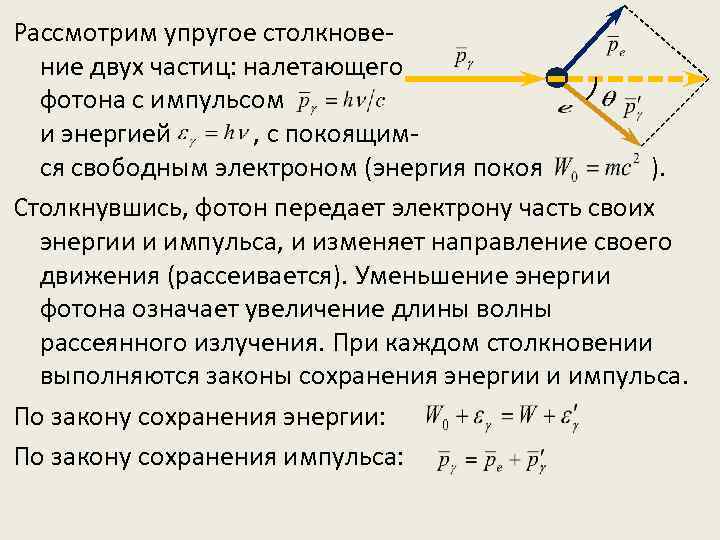Рассмотрим упругое столкновение двух частиц: налетающего фотона с импульсом и энергией , с покоящимся свободным электроном (энергия покоя ). Столкнувшись, фотон передает электрону часть своих энергии и импульса, и изменяет направление своего движения (рассеивается). Уменьшение энергии фотона означает увеличение длины волны рассеянного излучения. При каждом столкновении выполняются законы сохранения энергии и импульса. По закону сохранения энергии: По закону сохранения импульса:

– энергия электрона до столкновения – энергия налетающего фотона – энергия электрона после столкновения ( релятивистская формула) – энергия рассеянного фотона Подставив в исходные формулы значения величин, и выразив уравнение импульсов через схему, получим:

Решив приведенную выше систему получим: Так как , , , получим: Данное выражение – полученная экспериментально Комптоном формула

Наличие в составе рассеянного излучения первоначальной длины волны можно объяснить следующим образом. Предполагалось что соударение происходит со свободным электроном. Однако если электрон сильно связан с атомом, (справедливо для внутренних электронов тяжелых атомов), то фотон обменивается энергией не только с электроном, но и со всем атомом в целом. Так как масса атома по сравнению с массой электрона очень велика, то атому передаётся лишь ничтожная часть энергии фотона. Поэтому длина волны рассеянного излучения не будет сильно отличаться от длины волны падающего излучения. Эффект Комптона не наблюдается в видимой области спектра, так как энергия фотона видимого света сравнима с энергией связи электрона с атомом, при этом даже внешний электрон нельзя считать свободным.

Фотоэффект, эффект Комптона, свойства абсолютно черного тела – подтверждают квантовые представления о природе света. Интерференция, дифракция, поляризация – волновую (электромагнитную) природу света. Давление и преломление света объясняется как волновой, так и квантовой теориями. Таким образом, электромагнитное излучение обнаруживает единство, казалось взаимоисключающих свойств – непрерывных (волн) и дискретных (фотоны), которые взаимно допол -няют друга. Основные уравнения связывающие волновые и корпускулярные свойства света:

ЛЕКЦИЯ ОКОНЧЕНА СПАСИБО ЗА ВНИМАНИЕ !