Лекция 12 Тени на архитектурных деталях Построение падающих

Лекция 12 Тени на архитектурных деталях Построение падающих и собственных теней: • на телах вращения • на лестнице • на колоннах • на наклонных плоскостях крыш

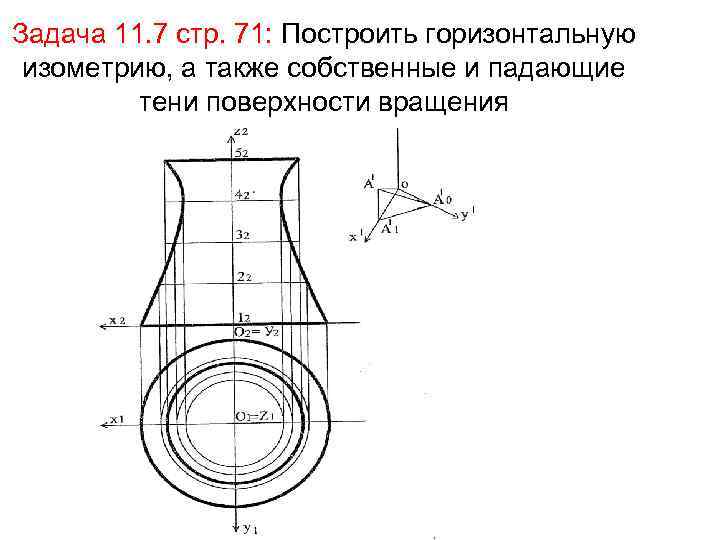Задача 11. 7 стр. 71: Построить горизонтальную изометрию, а также собственные и падающие тени поверхности вращения

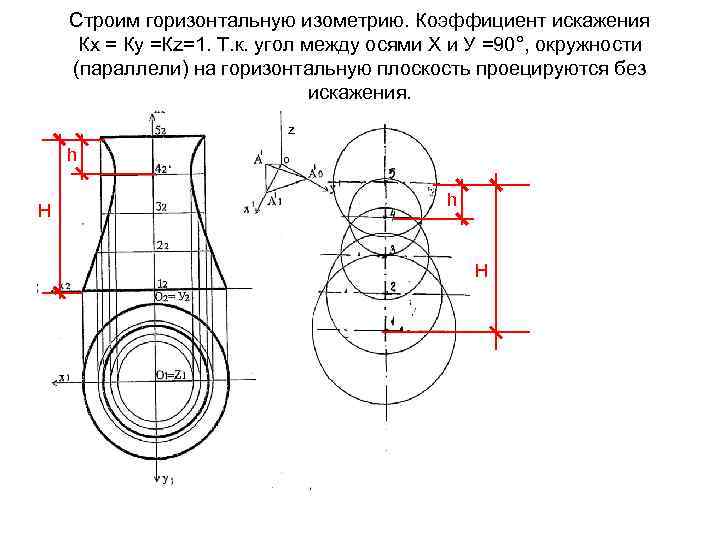Строим горизонтальную изометрию. Коэффициент искажения Кх = Ку =Кz=1. Т. к. угол между осями Х и У =90°, окружности (параллели) на горизонтальную плоскость проецируются без искажения. z h H

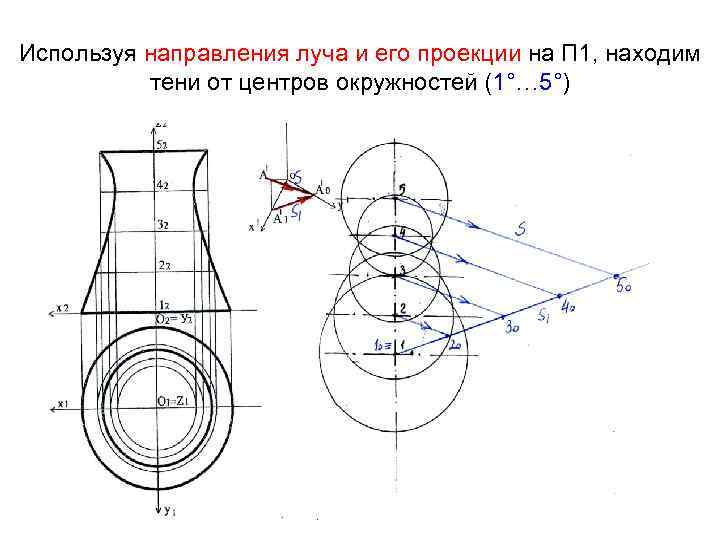Используя направления луча и его проекции на П 1, находим тени от центров окружностей (1°… 5°)

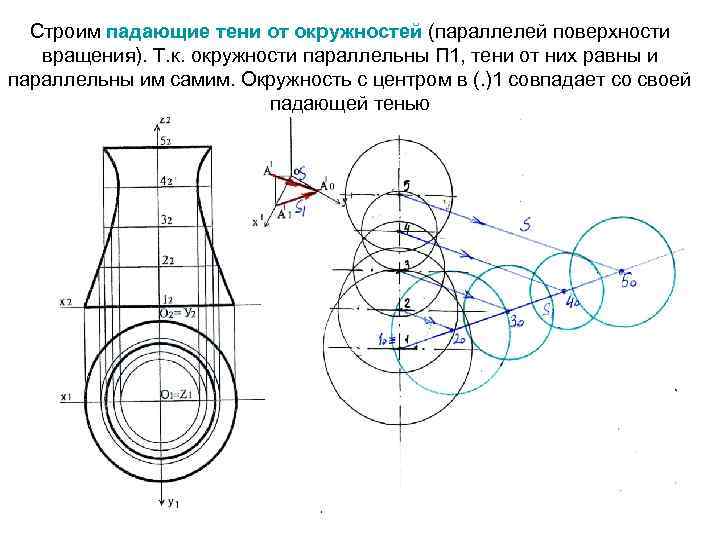Строим падающие тени от окружностей (параллелей поверхности вращения). Т. к. окружности параллельны П 1, тени от них равны и параллельны им самим. Окружность с центром в (. )1 совпадает со своей падающей тенью

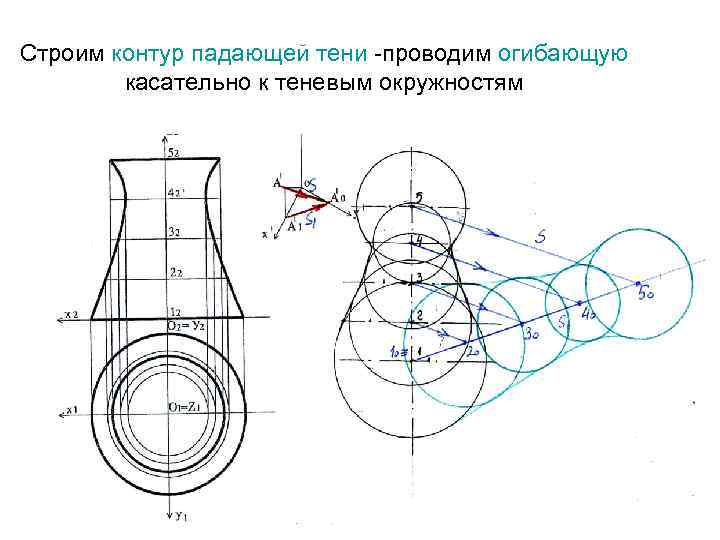Строим контур падающей тени -проводим огибающую касательно к теневым окружностям

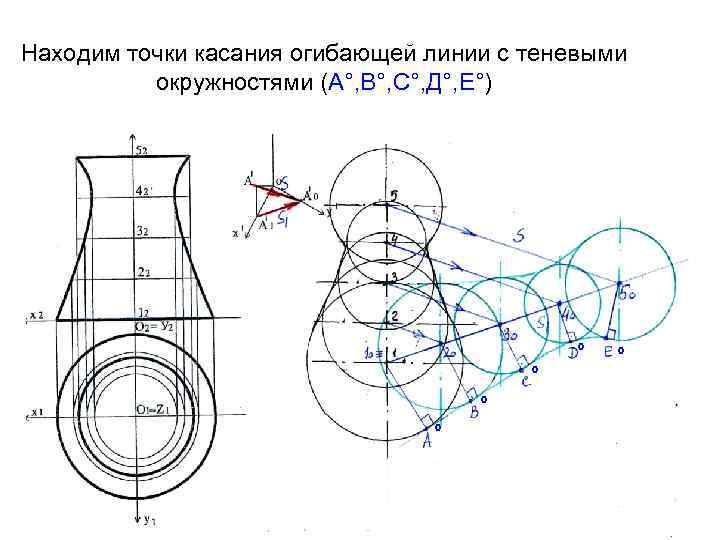Находим точки касания огибающей линии с теневыми окружностями (А°, В°, С°, Д°, Е°) ° ° °

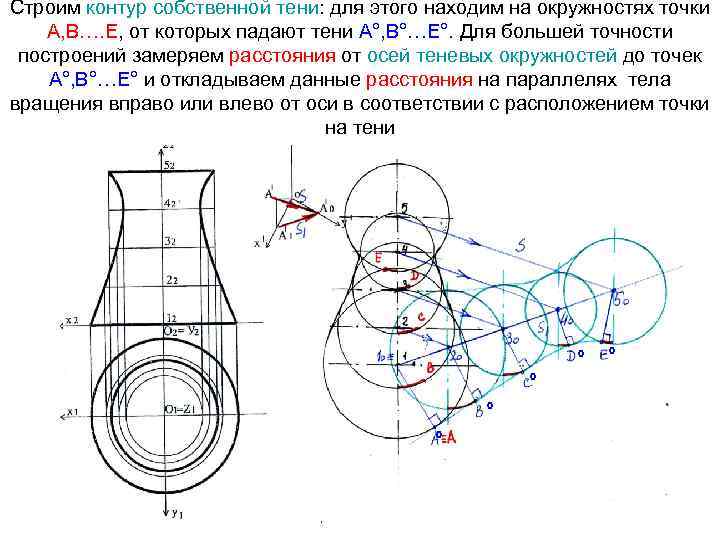Строим контур собственной тени: для этого находим на окружностях точки А, В…. Е, от которых падают тени А°, В°…Е°. Для большей точности построений замеряем расстояния от осей теневых окружностей до точек А°, В°…Е° и откладываем данные расстояния на параллелях тела вращения вправо или влево от оси в соответствии с расположением точки на тени ° ° °

° ° °

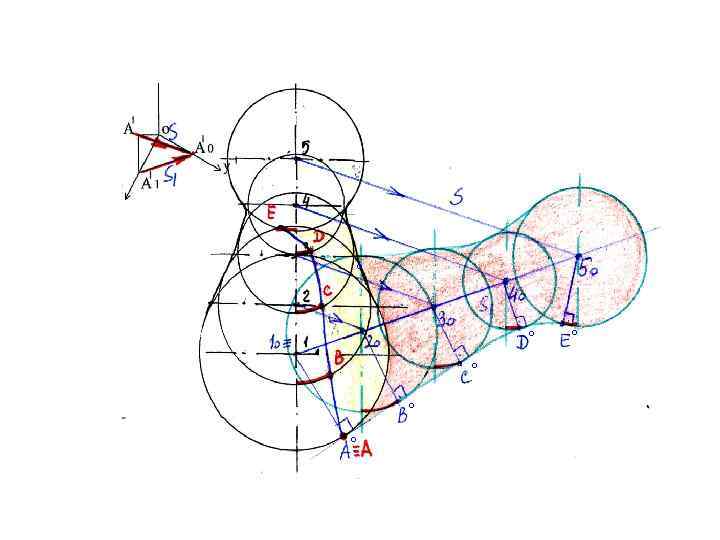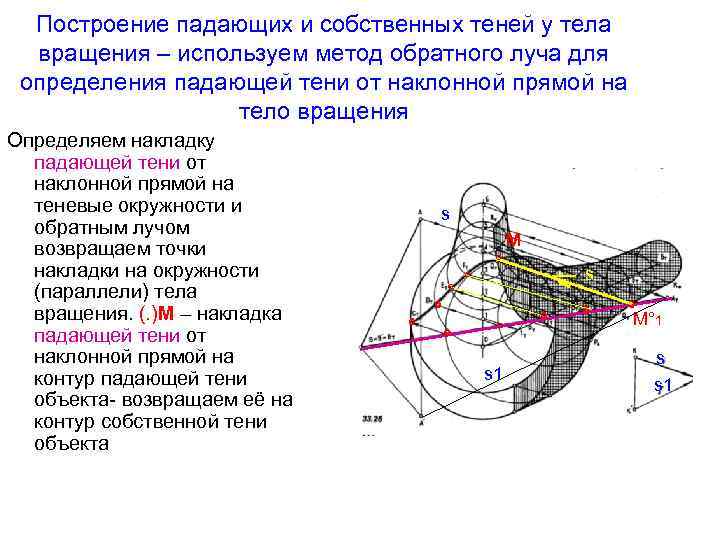Построение падающих и собственных теней у тела вращения – используем метод обратного луча для определения падающей тени от наклонной прямой на тело вращения Определяем накладку падающей тени от наклонной прямой на теневые окружности и обратным лучом возвращаем точки накладки на окружности (параллели) тела вращения. (. )М – накладка падающей тени от наклонной прямой на контур падающей тени объекта- возвращаем её на контур собственной тени объекта s М ° ° ° ° s 1 s ° ° °М° 1 s s 1

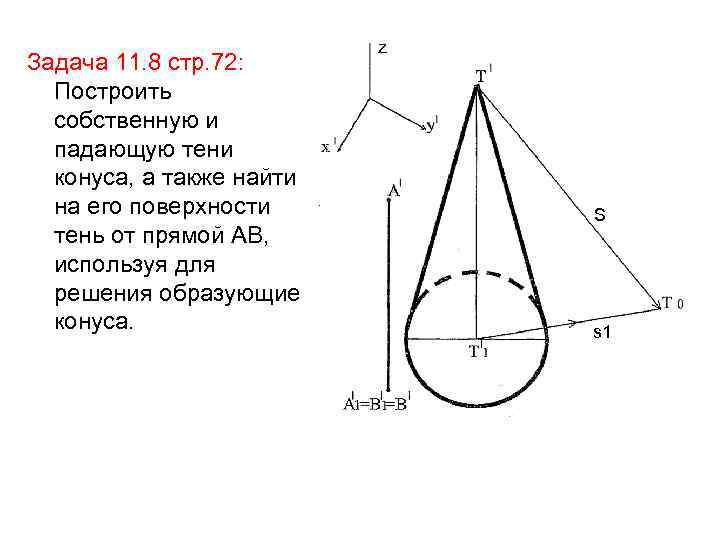Задача 11. 8 стр. 72: Построить собственную и падающую тени конуса, а также найти на его поверхности тень от прямой АВ, используя для решения образующие конуса. z S s 1

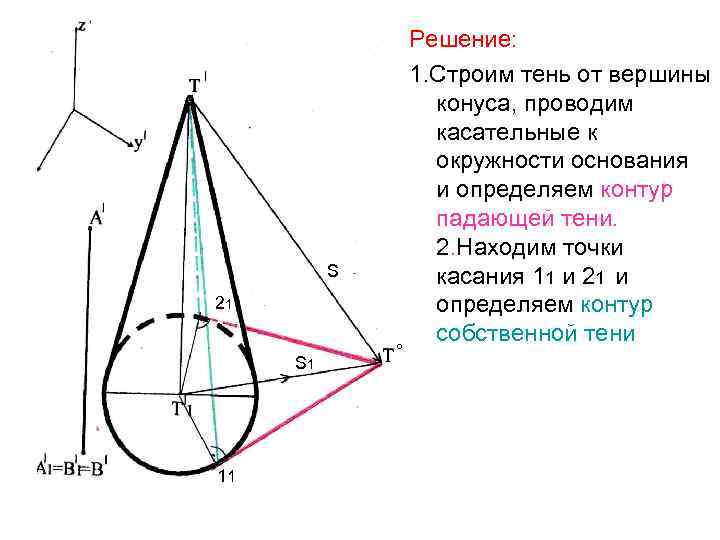S 21 S 1 11 ° Решение: 1. Строим тень от вершины конуса, проводим касательные к окружности основания и определяем контур падающей тени. 2. Находим точки касания 11 и 21 и определяем контур собственной тени

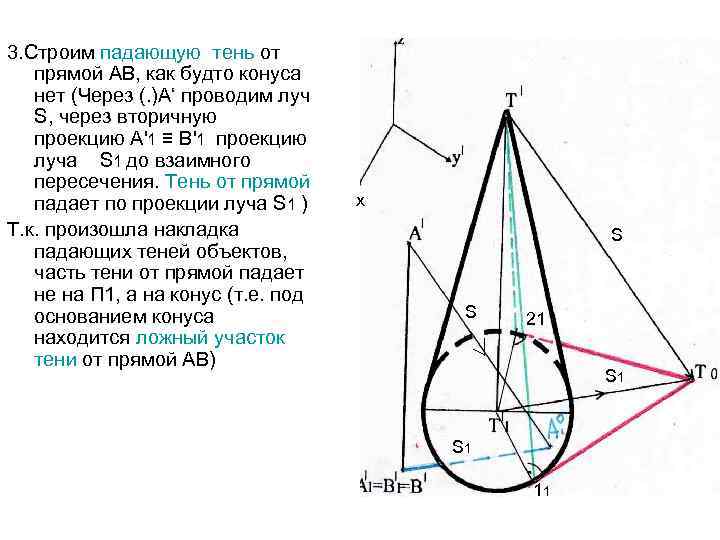3. Строим падающую тень от прямой АВ, как будто конуса нет (Через (. )А‘ проводим луч S, через вторичную проекцию А'1 ≡ В'1 проекцию луча S 1 до взаимного пересечения. Тень от прямой падает по проекции луча S 1 ) Т. к. произошла накладка падающих теней объектов, часть тени от прямой падает не на П 1, а на конус (т. е. под основанием конуса находится ложный участок тени от прямой АВ) х S S 21 S 1 11

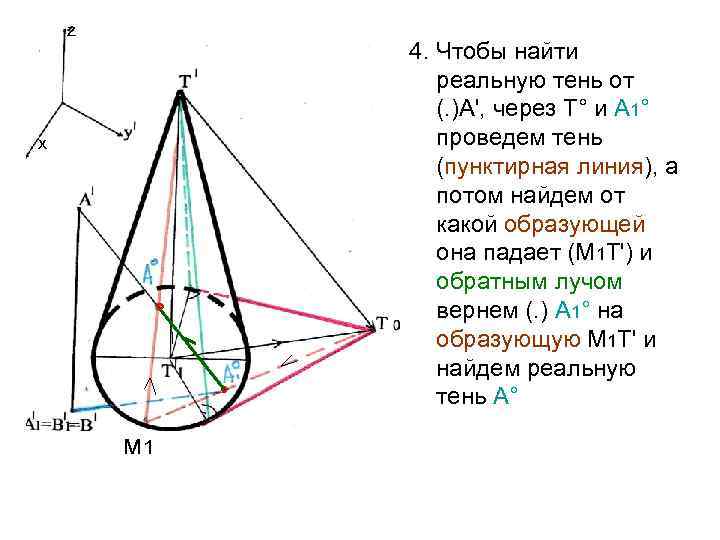z x ° ° м 1 4. Чтобы найти реальную тень от (. )А', через Т° и А 1° проведем тень (пунктирная линия), а потом найдем от какой образующей она падает (М 1 Т') и обратным лучом вернем (. ) А 1° на образующую М 1 Т' и найдем реальную тень А°

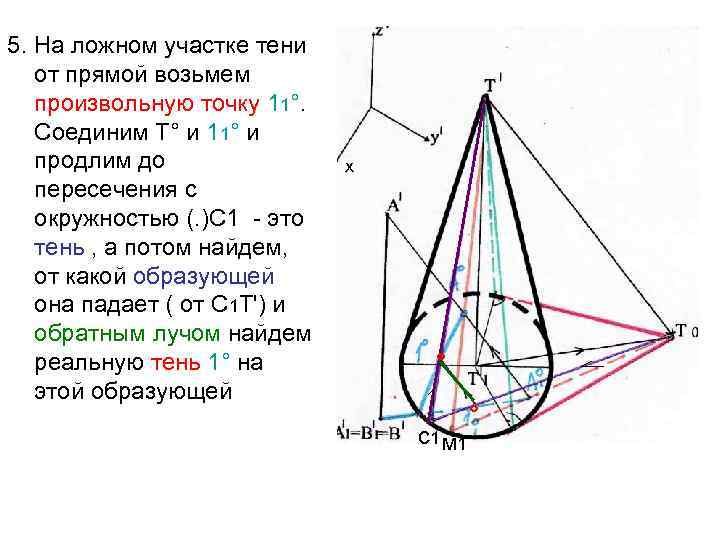5. На ложном участке тени от прямой возьмем произвольную точку 11°. Соединим Т° и 11° и продлим до пересечения с окружностью (. )С 1 - это тень , а потом найдем, от какой образующей она падает ( от С 1 Т') и обратным лучом найдем реальную тень 1° на этой образующей х ° с1 м 1 °

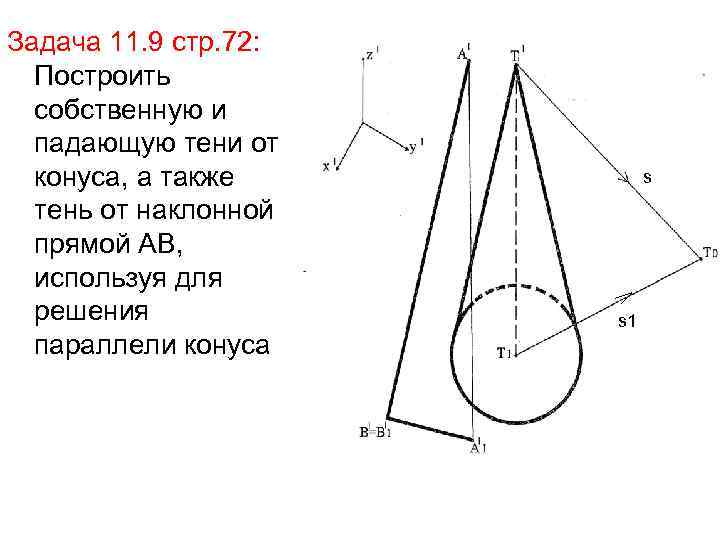Задача 11. 9 стр. 72: Построить собственную и падающую тени от конуса, а также тень от наклонной прямой АВ, используя для решения параллели конуса s s 1

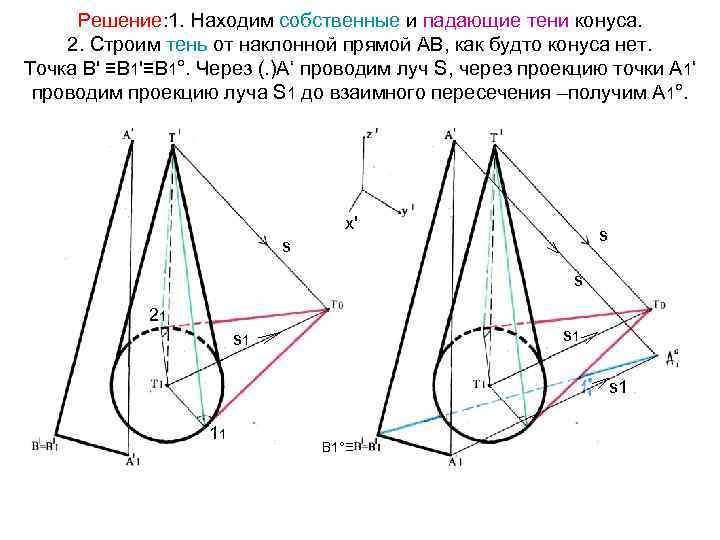Решение: 1. Находим собственные и падающие тени конуса. 2. Строим тень от наклонной прямой АВ, как будто конуса нет. Точка В' ≡В 1'≡В 1°. Через (. )А‘ проводим луч S, через проекцию точки А 1‘ проводим проекцию луча S 1 до взаимного пересечения –получим А 1°. х' s s s 21 s 1 s 1 11 В 1°≡

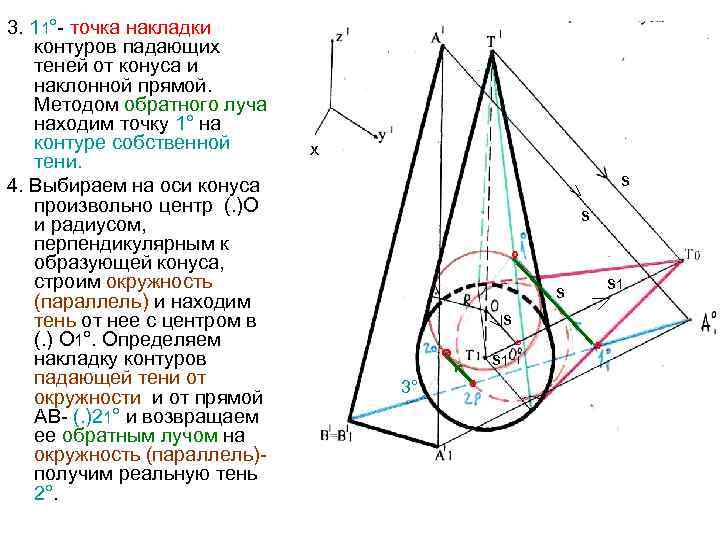3. 11°- точка накладки контуров падающих теней от конуса и наклонной прямой. Методом обратного луча находим точку 1° на контуре собственной тени. 4. Выбираем на оси конуса произвольно центр (. )О и радиусом, перпендикулярным к образующей конуса, строим окружность (параллель) и находим тень от нее с центром в (. ) О 1°. Определяем накладку контуров падающей тени от окружности и от прямой АВ- (. )21° и возвращаем ее обратным лучом на окружность (параллель)получим реальную тень 2°. х s s ° s 1 s s ° 3° s 1 ° ° °

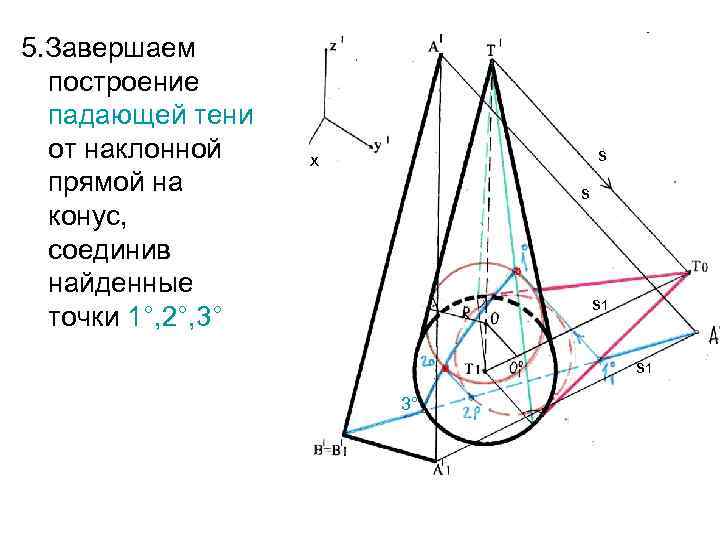5. Завершаем построение падающей тени от наклонной прямой на конус, соединив найденные точки 1°, 2°, 3° s х s ° s 1 ° 3° s 1

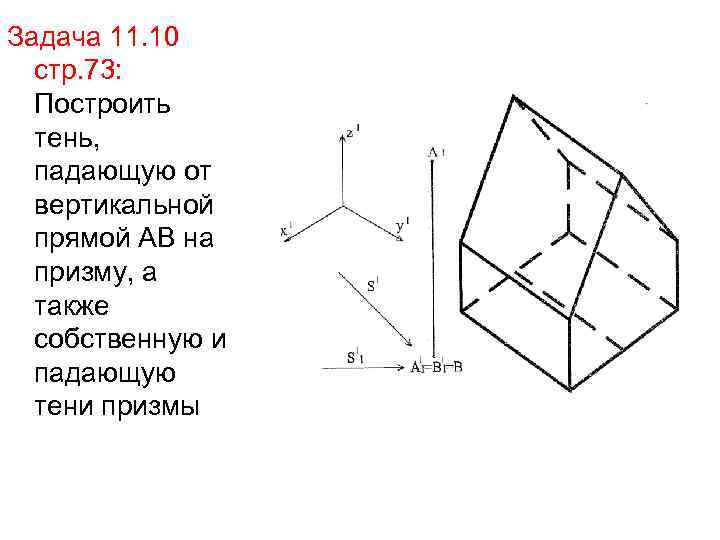Задача 11. 10 стр. 73: Построить тень, падающую от вертикальной прямой АВ на призму, а также собственную и падающую тени призмы

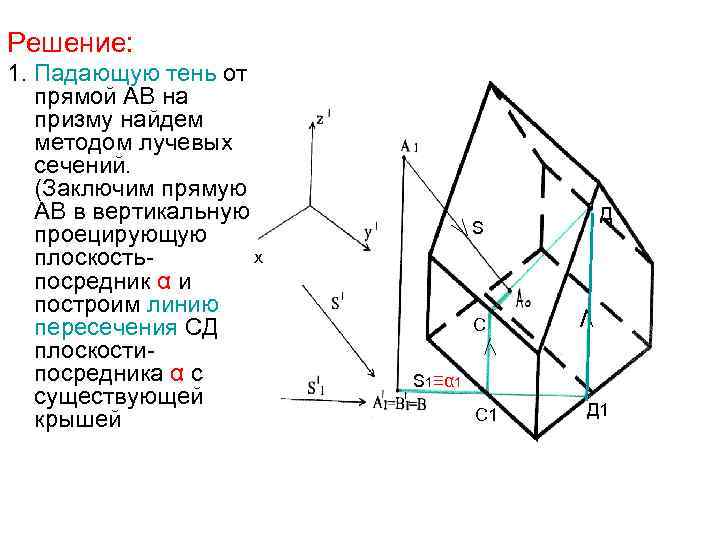Решение: 1. Падающую тень от прямой АВ на призму найдем методом лучевых сечений. (Заключим прямую АВ в вертикальную проецирующую х плоскостьпосредник α и построим линию пересечения СД плоскостипосредника α с существующей крышей S Д С S 1 ≡α 1 С 1 Д 1

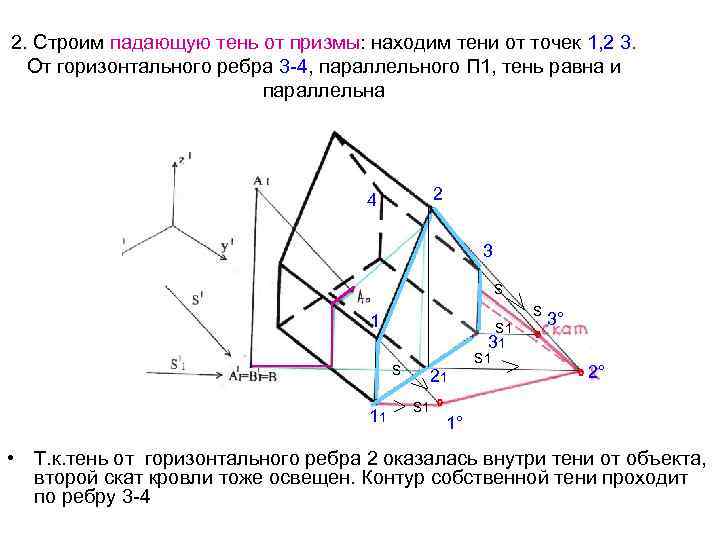2. Строим падающую тень от призмы: находим тени от точек 1, 2 3. От горизонтального ребра 3 -4, параллельного П 1, тень равна и параллельна 2 4 3 S S 11 21 S 1 ° S 1 31 S 1 ° 3° ° 2° 1° • Т. к. тень от горизонтального ребра 2 оказалась внутри тени от объекта, второй скат кровли тоже освещен. Контур собственной тени проходит по ребру 3 -4

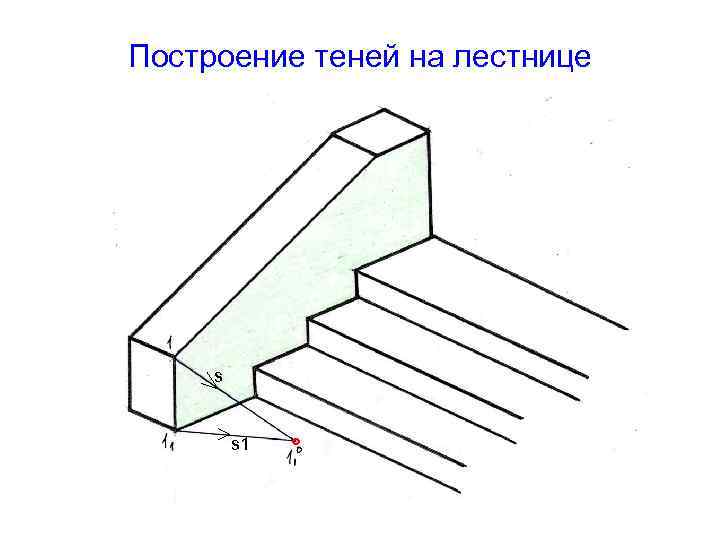Построение теней на лестнице s s 1 °

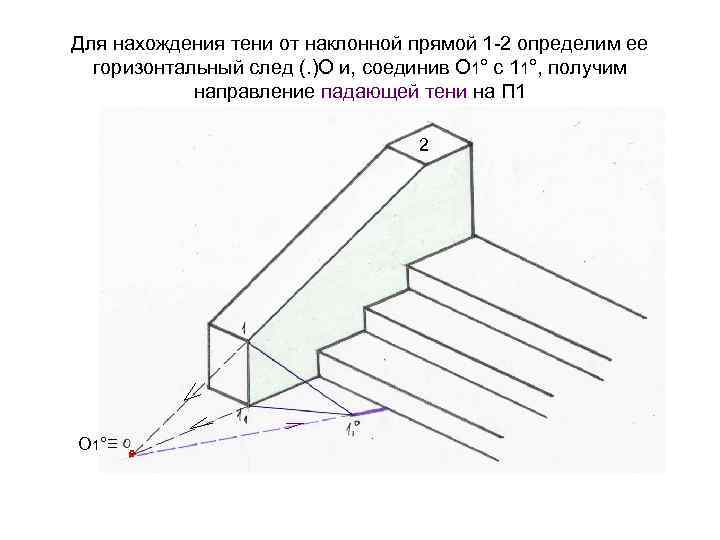Для нахождения тени от наклонной прямой 1 -2 определим ее горизонтальный след (. )О и, соединив О 1° с 11°, получим направление падающей тени на П 1 2 О 1°≡ °

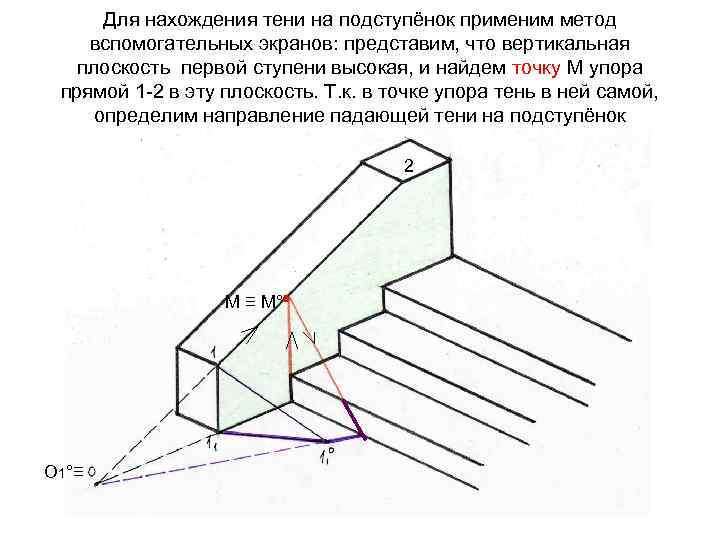Для нахождения тени на подступёнок применим метод вспомогательных экранов: представим, что вертикальная плоскость первой ступени высокая, и найдем точку М упора прямой 1 -2 в эту плоскость. Т. к. в точке упора тень в ней самой, определим направление падающей тени на подступёнок 2 М ≡ М°° О 1°≡

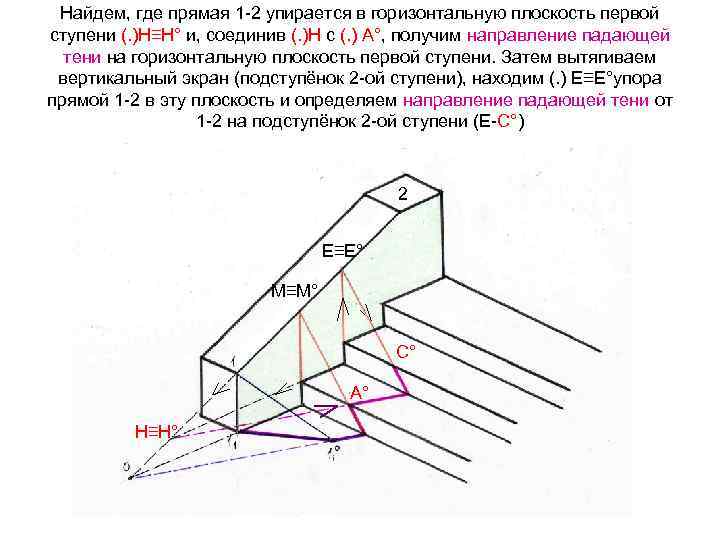Найдем, где прямая 1 -2 упирается в горизонтальную плоскость первой ступени (. )Н≡Н° и, соединив (. )Н с (. ) А°, получим направление падающей тени на горизонтальную плоскость первой ступени. Затем вытягиваем вертикальный экран (подступёнок 2 -ой ступени), находим (. ) Е≡Е°упора прямой 1 -2 в эту плоскость и определяем направление падающей тени от 1 -2 на подступёнок 2 -ой ступени (Е-С°) 2 Е≡Е° М≡М° С° А° Н≡Н°

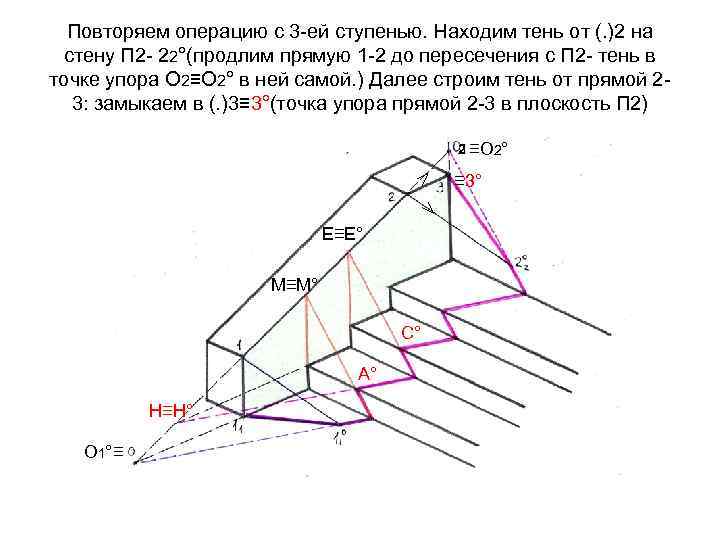Повторяем операцию с 3 -ей ступенью. Находим тень от (. )2 на стену П 2 - 22°(продлим прямую 1 -2 до пересечения с П 2 - тень в точке упора О 2≡О 2° в ней самой. ) Далее строим тень от прямой 23: замыкаем в (. )3≡ 3°(точка упора прямой 2 -3 в плоскость П 2) 2 ≡О 2° ≡ 3° Е≡Е° М≡М° С° А° Н≡Н° О 1°≡

Построение собственной и падающей тени на колонне с квадратной плитой S

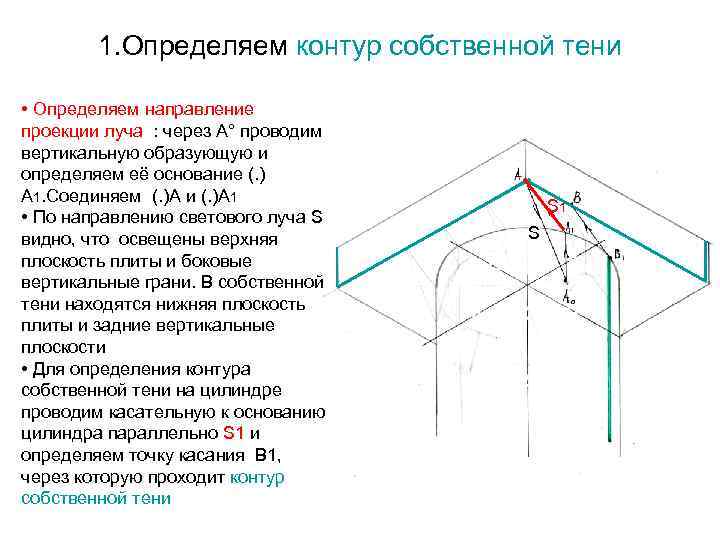1. Определяем контур собственной тени • Определяем направление проекции луча : через А° проводим вертикальную образующую и определяем её основание (. ) А 1. Соединяем (. )А и (. )А 1 • По направлению светового луча S видно, что освещены верхняя плоскость плиты и боковые вертикальные грани. В собственной тени находятся нижняя плоскость плиты и задние вертикальные плоскости • Для определения контура собственной тени на цилиндре проводим касательную к основанию цилиндра параллельно S 1 и определяем точку касания В 1, через которую проходит контур собственной тени S 1 S

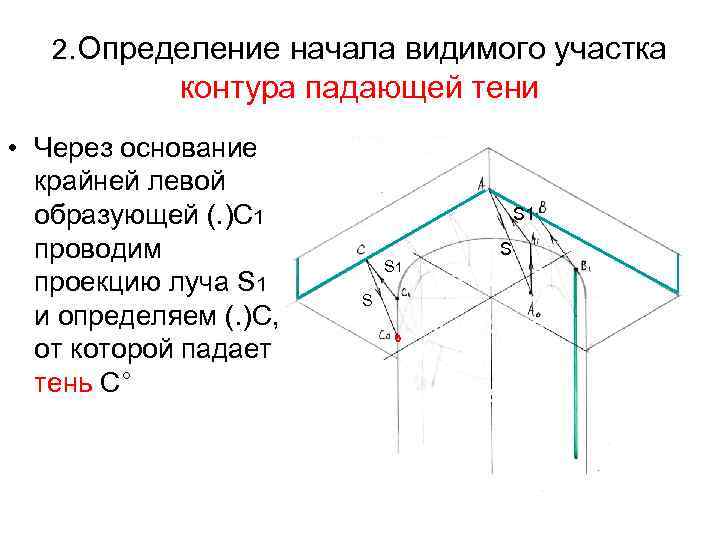2. Определение начала видимого участка контура падающей тени • Через основание крайней левой образующей (. )С 1 проводим проекцию луча S 1 и определяем (. )С, от которой падает тень С° S 1 S ° S

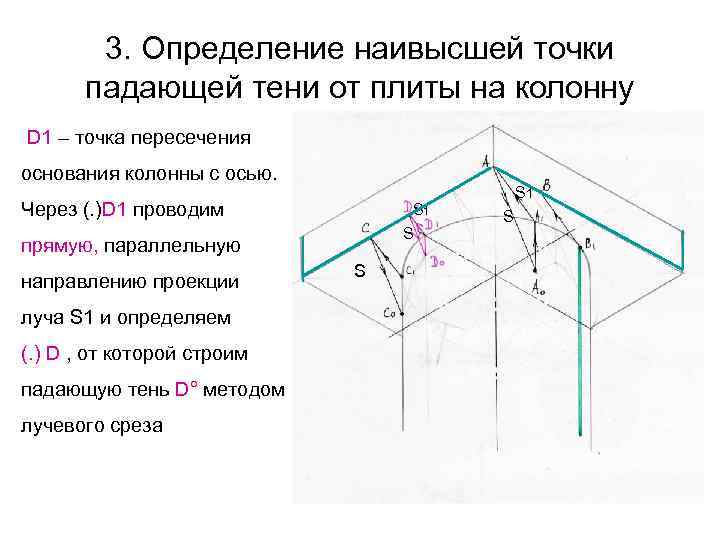3. Определение наивысшей точки падающей тени от плиты на колонну D 1 – точка пересечения основания колонны с осью. Через (. )D 1 проводим S 1 S прямую, параллельную направлению проекции луча S 1 и определяем (. ) D , от которой строим падающую тень D° методом лучевого среза S S 1 S

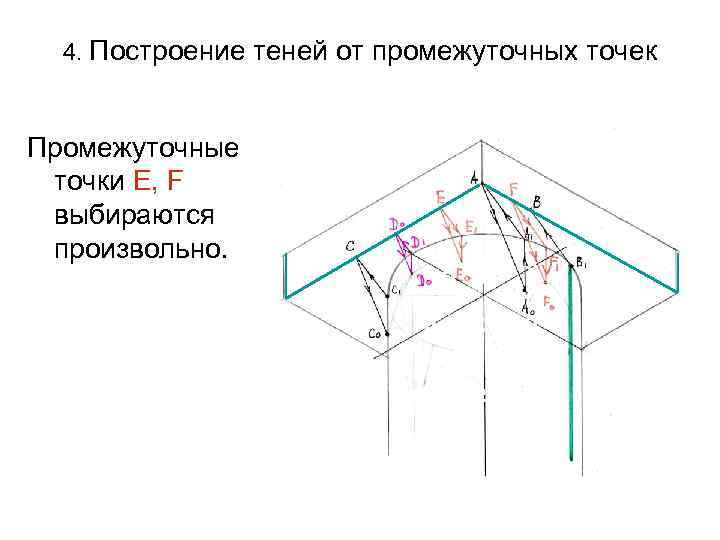4. Построение теней от промежуточных точек Промежуточные точки Е, F выбираются произвольно.

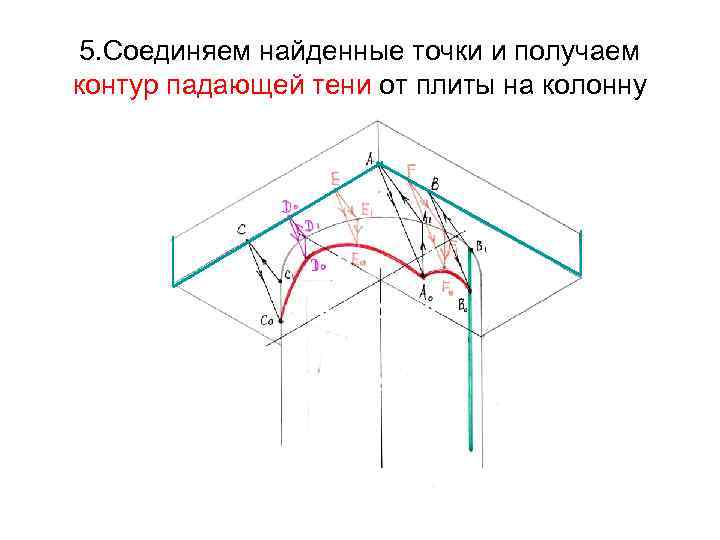5. Соединяем найденные точки и получаем контур падающей тени от плиты на колонну

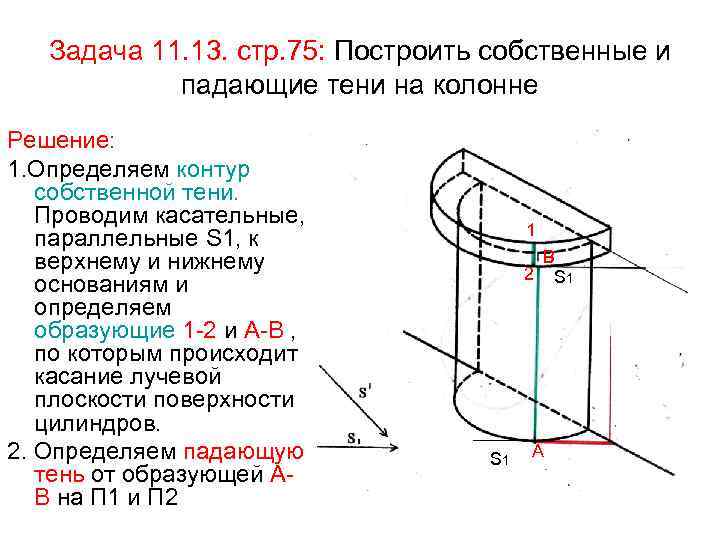Задача 11. 13. стр. 75: Построить собственные и падающие тени на колонне Решение: 1. Определяем контур собственной тени. Проводим касательные, параллельные S 1, к верхнему и нижнему основаниям и определяем образующие 1 -2 и А-В , по которым происходит касание лучевой плоскости поверхности цилиндров. 2. Определяем падающую тень от образующей АВ на П 1 и П 2 1 В 2 S 1 А

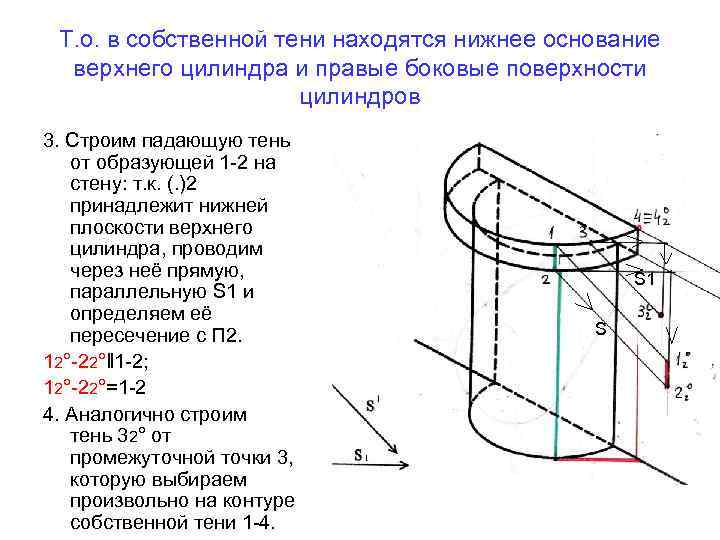Т. о. в собственной тени находятся нижнее основание верхнего цилиндра и правые боковые поверхности цилиндров 3. Строим падающую тень от образующей 1 -2 на стену: т. к. (. )2 принадлежит нижней плоскости верхнего цилиндра, проводим через неё прямую, параллельную S 1 и определяем её пересечение с П 2. 12°-22°‖ 1 -2; 12°-22°=1 -2 4. Аналогично строим тень 32° от промежуточной точки 3, которую выбираем произвольно на контуре собственной тени 1 -4. S 1 S

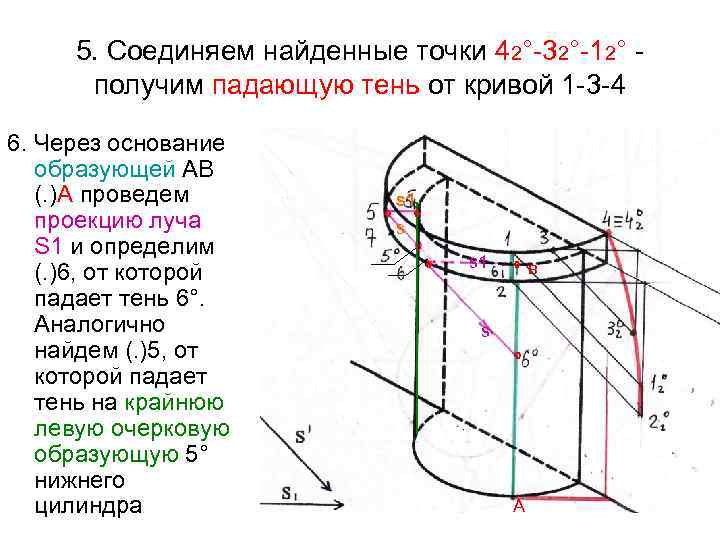5. Соединяем найденные точки 42°-32°-12° получим падающую тень от кривой 1 -3 -4 6. Через основание образующей АВ (. )А проведем проекцию луча S 1 и определим (. )6, от которой падает тень 6°. Аналогично найдем (. )5, от которой падает тень на крайнюю левую очерковую образующую 5° нижнего цилиндра s 1 °s ° ° ° s 1 °в s ° А

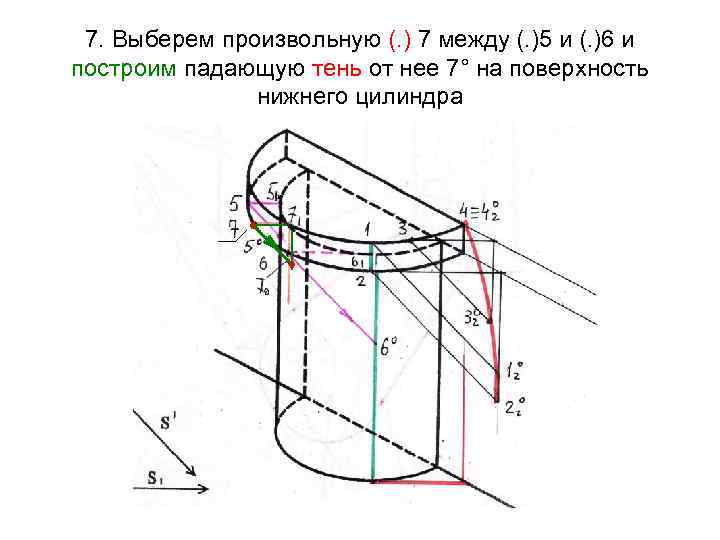7. Выберем произвольную (. ) 7 между (. )5 и (. )6 и построим падающую тень от нее 7° на поверхность нижнего цилиндра ° °

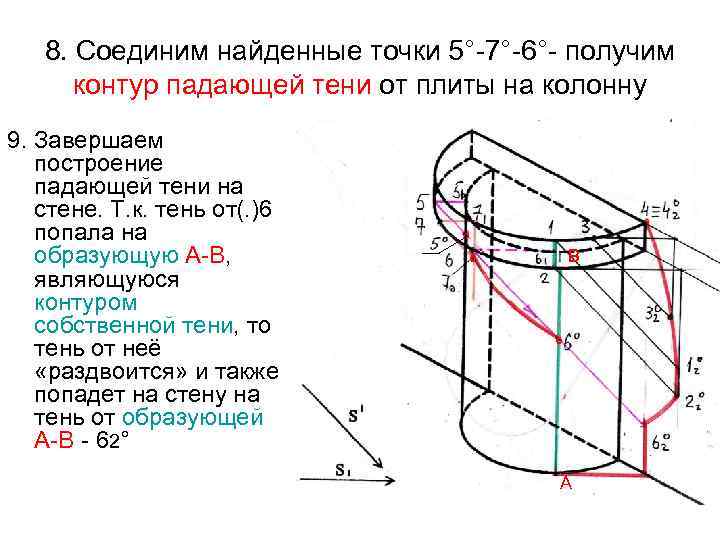8. Соединим найденные точки 5°-7°-6°- получим контур падающей тени от плиты на колонну 9. Завершаем построение падающей тени на стене. Т. к. тень от(. )6 попала на образующую А-В, являющуюся контуром собственной тени, то тень от неё «раздвоится» и также попадет на стену на тень от образующей А-В - 62° ° В ° ° А

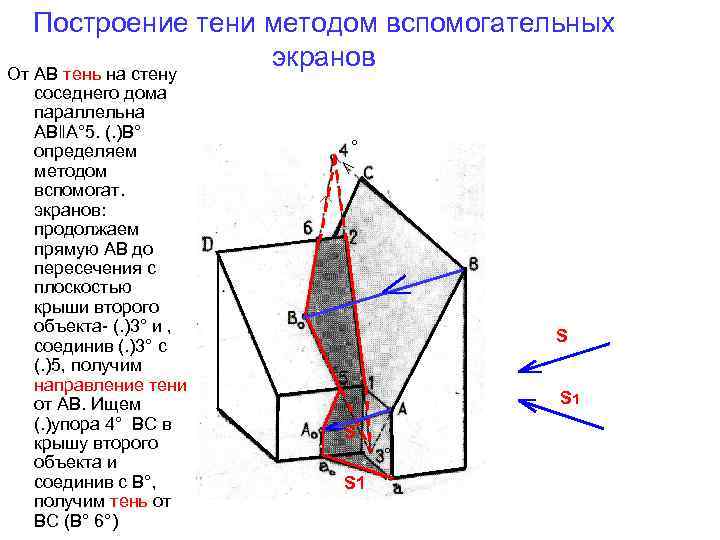Построение тени методом вспомогательных экранов От АВ тень на стену соседнего дома параллельна АВ‖А° 5. (. )В° определяем методом вспомогат. экранов: продолжаем прямую АВ до пересечения с плоскостью крыши второго объекта- (. )3° и , соединив (. )3° с (. )5, получим направление тени от АВ. Ищем (. )упора 4° ВС в крышу второго объекта и соединив с В°, получим тень от ВС (В° 6°) ° S S 1 S ° S 1