Лекция 12 Преобразование Лапласа Оригиналы и изображения Законы

Лекция 12 Преобразование Лапласа. Оригиналы и изображения. Законы Кирхгофа в операторной форме Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА переходных процессов в линейных электрических цепях 2 Операторный метод предусматривает переход от функций времени f(t), называемых оригиналами, к функциям F(p) – изображениям. Такой переход называется прямым преобразованием. Используется и обратный переход от изображений к оригиналам – обратное преобразование. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

3 Прямое преобразование переводит дифференциальные уравнения электрических цепей в линейные алгебраические уравнения, решение которых осуществляется более просто. Обратное преобразование позволяет получить искомые токи и (или) напряжения – функции времени – по полученным изображениям. Изображения обозначаются прописными (большими) буквами. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Изображения получают с помощью интеграла Лапласа 4 где p – комплексная переменная. Достоинством преобразования по Лапласу является его соответствие с преобразованием Фурье, на котором основывается широко используемый в настоящее время частотный метод анализа цепей. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

5 Соответствие между оригиналом f(t) и изображением F(p) принято записывать в следующем виде: где L – символическое обозначение преобразования Лапласа. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

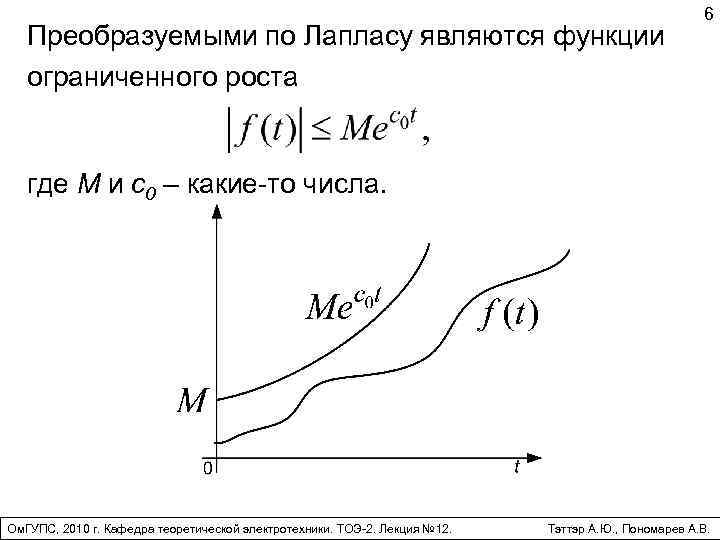
Преобразуемыми по Лапласу являются функции ограниченного роста 6 где M и c 0 – какие-то числа. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Преобразование Лапласа является линейным, поэтому оно обладает следующими свойствами. 7 1. Сумме оригиналов соответствует сумма изображений: 2. Произведению оригинала на постоянный множитель соответствует умножение изображения на тот же множитель: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Изображения некоторых функций 8 1. Постоянное напряжение U Применение (1) дает: следовательно Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

2. Экспонента Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 9 Тэттэр А. Ю. , Пономарев А. В.

3. Синусоида Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 10 Тэттэр А. Ю. , Пономарев А. В.

11 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

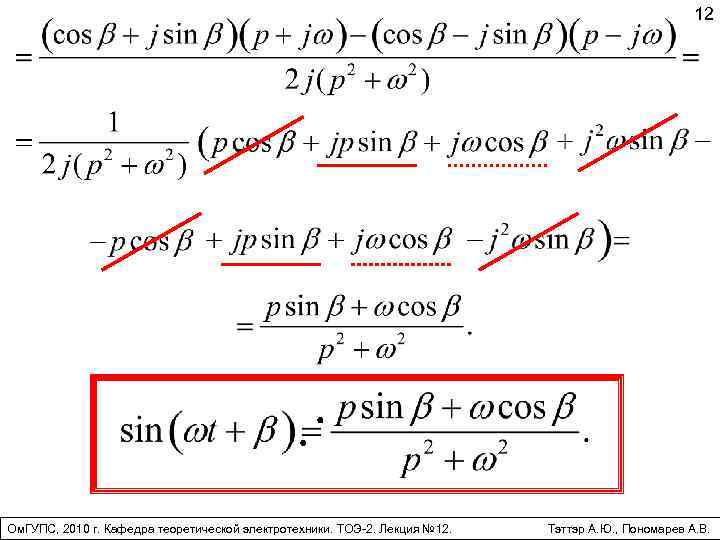
12 Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

13 4. Производная Используем формулу интегрирования по частям: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

14 Используя полученные соотношения, можно перейти от уравнений, записанных по законам Кирхгофа для оригиналов, к уравнениям для изображений. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Активное сопротивление Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 15 Тэттэр А. Ю. , Пономарев А. В.

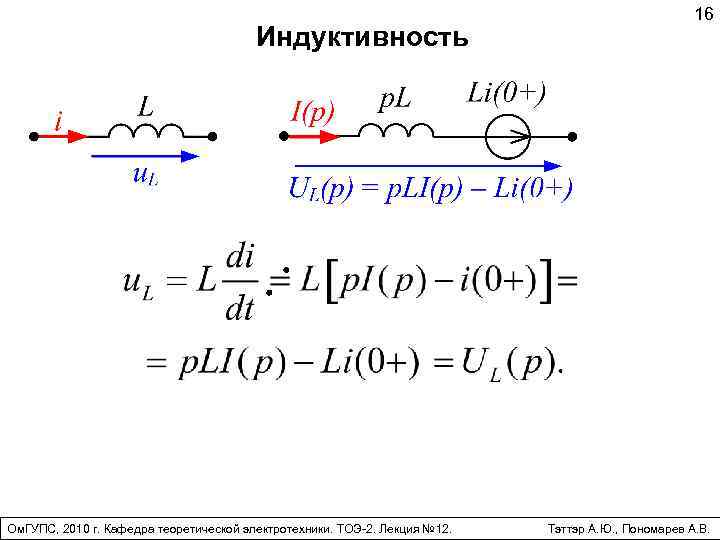
Индуктивность Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 16 Тэттэр А. Ю. , Пономарев А. В.

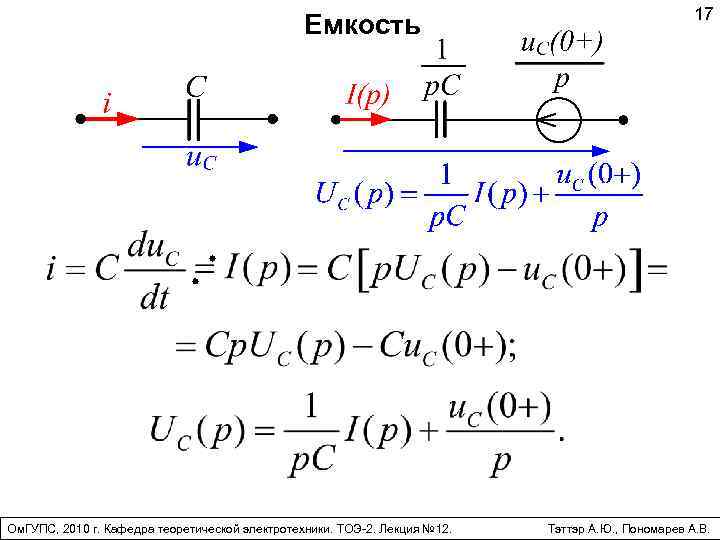
Емкость Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 17 Тэттэр А. Ю. , Пономарев А. В.

Источник постоянного напряжения 18 Источник синусоидального напряжения Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Законы Кирхгофа в операторной форме 19 Первый закон Кирхгофа (для узла цепи) имеет вид: где ik – ток k-й ветви. В операторной форме: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

20 Второй закон Кирхгофа (для контура) имеет вид: где ek – алгебраическая сумма ЭДС источников энергии в k-й ветви, а uk – напряжение на k-й ветви. В операторной форме: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

21 При составлении уравнений Кирхгофа в операторной форме необходимо задаться положительными направлениями изображений всех токов и соблюдать все правила знаков, установленные ранее при составлении законов Кирхгофа для функций времени (оригиналов). Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

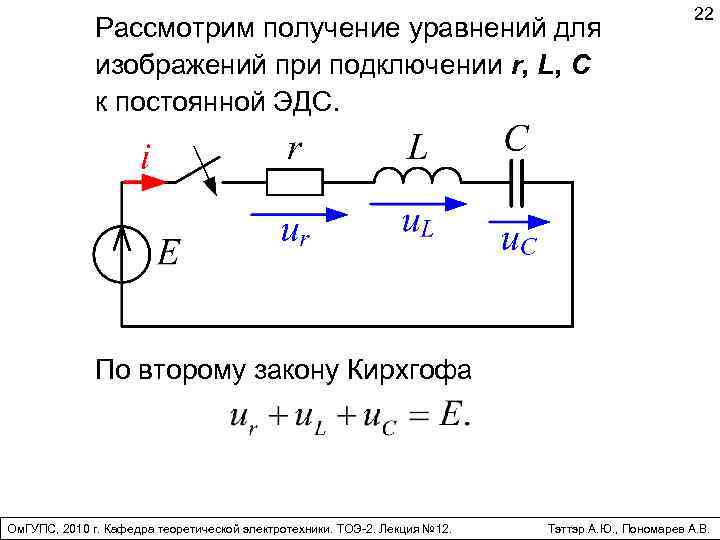
Рассмотрим получение уравнений для изображений при подключении r, L, C к постоянной ЭДС. 22 По второму закону Кирхгофа Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

23 В данном примере: Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

24 Уравнение для изображений: (2) Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.

Такое же уравнение можно сформировать по операторной схеме замещения, учитывая, что i(0+)=0, u. C(0+)=0. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. 25 Тэттэр А. Ю. , Пономарев А. В.

26 Величину называют операторным сопротивлением ветви. Ом. ГУПС, 2010 г. Кафедра теоретической электротехники. ТОЭ-2. Лекция № 12. Тэттэр А. Ю. , Пономарев А. В.