12_22.11.pptx
- Количество слайдов: 18

ЛЕКЦИЯ 12 Образ и прообраз множества при данном соответствии 21. 11. 2012 г.

• Пусть дано соответствие Г = (X, Y, F). • Образом элемента х Х при соответствии Г называется и через Г(х) обозначается множество элементов y Y, для которых пара <x, y> F. Иначе, Г(х)={y Y|<x, y> F}. Т. е. , образ элемента х Х – это множество тех элементов y Y, которые соответствуют элементу x. • На графе образ элемента x можно представить как множество тех вершин y, в которые входят дуги, выходящие из вершины x.
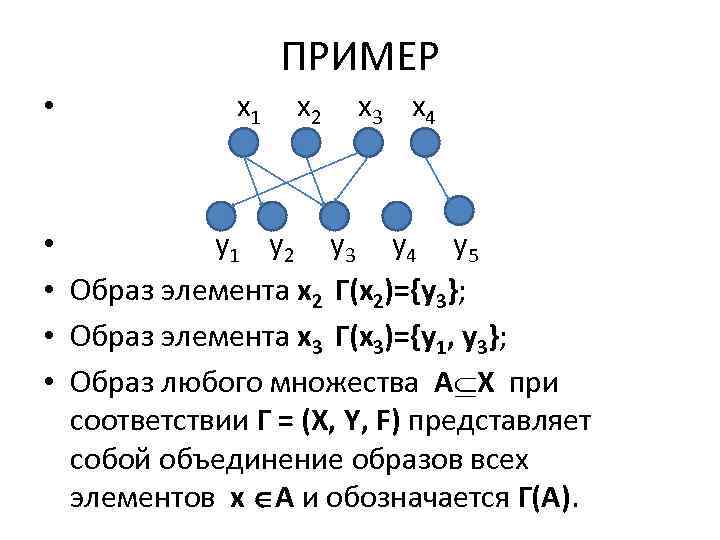
ПРИМЕР • x 1 x 2 x 3 x 4 • y 1 y 2 y 3 y 4 y 5 • Образ элемента x 2 Г(x 2)={y 3}; • Образ элемента x 3 Г(x 3)={y 1, y 3}; • Образ любого множества A X при соответствии Г = (X, Y, F) представляет собой объединение образов всех элементов x A и обозначается Г(А).

• В общем случае справедливо: • Г(А) = Г(х) • х А • Для рассмотренного примера если А={x 2, x 3}, то Г(А)=Г(х2) Г(х3)={y 3} {y 1, y 3}={y 1, y 3}. • Пусть дано соответствие Г = (X, Y, F). • Прообразом элемента y Y при соответствии Г называется и через Г-1(y) обозначается множество элементов x X, для которых пара <x, y> F.

5 • Таким образом, Г-1(y)={x X|<x, y> F } – это множество тех элементов из Х, которым соответствует элемент y. • На графе прообраз элемента y можно представить множеством тех вершин х, из которых выходят дуги, заходящие в вершину y. Для рассмотренного примера • Г-1(y 3)={x 1, x 2, x 3}, Г(y 4)= .

6 • Прообразом произвольного множества B Y при соответствии Г = (X, Y, F) называется объединение прообразов всех элементов y B и обозначается Г-1(В), т. е. • Г-1(В) = Г-1(y) • y B • Если В={y 3, y 4, y 5}, то при соответствии Г для рассмотренного примера прообраз запишется • Г-1(В)={x 1, x 2, x 3, x 4}.

7 • Пусть Г = (X, Y, F) – произвольное соответствие и А – произвольное подмножество множества Х. • Сужением соответствия Г на множество А называется и через ГА обозначается соответствие, график которого FA определяется выражением: • FA = (A Y) F, т. е. ГА = (X, Y, FA). • Соответствие ГА Г. Соответствие Г в этом случае называют продолжением соответствия ГА на множество Х.

Основные свойства соответствий • 1. ФУНКЦИОНАЛЬНОСТЬ: • Соответствие Г = (X, Y, F) называется функциональным, если для любого х Х образ Г(х) содержит не более одного элемента y Y, в противном случае соответствие называется нефункциональным.
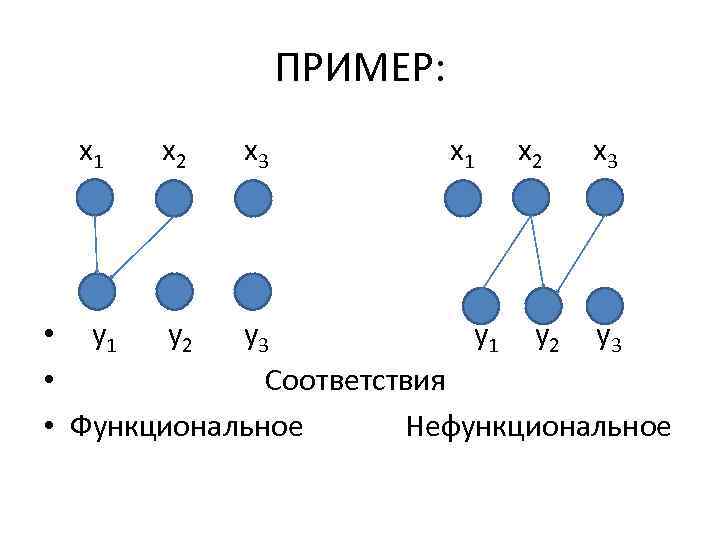
ПРИМЕР: x 1 x 2 x 3 • y 1 y 2 y 3 • Соответствия • Функциональное Нефункциональное

10 • 2. ИНЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется инъективным, если для любого y Y прообраз Г-1(y) содержит не более одного элемента х Х, в противном случае соответствие называется неинъективным.
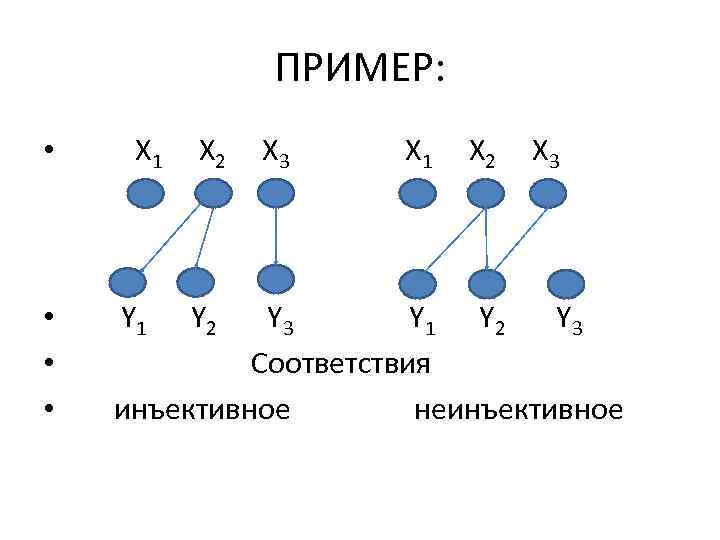
ПРИМЕР: • • X 1 Y 1 X 2 Y 2 X 3 X 1 X 2 X 3 Y 1 Y 2 Y 3 Соответствия инъективное неинъективное

12 • 3. ОПРЕДЕЛЕННОСТЬ: • Соответствие Г = (X, Y, F) называется всюду определенным, если для каждого х Х образ Г(х) , в противном случае соответствие не всюду определено. • В графе всюду определенного соответствия из каждой вершины х Х выходит хотя бы одна дуга.

13 • 4. СЮРЪЕКТИВНОСТЬ: • Соответствие Г = (X, Y, F) называется сюръективным, если для любого элемента y Y прообраз Г-1(y) , в противном случае соответствие несюръективно. • В графе сюръективного соответствия в каждую вершину, соответствующую y Y, входит хотя бы одно ребро (дуга, стрелка). • Если соответствие одновременно функциональное, инъективное, всюду определенное и сюръективное, то оно называется взаимно-однозначным или биективным.
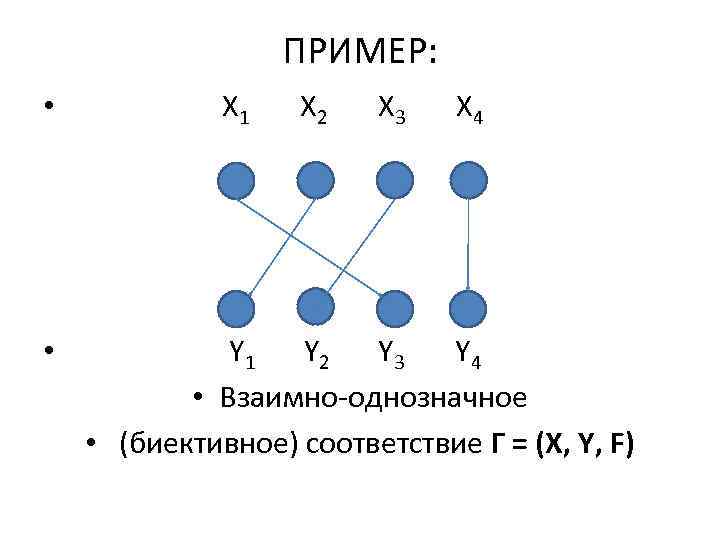
ПРИМЕР: • • X 1 X 2 X 3 X 4 Y 1 Y 2 Y 3 Y 4 • Взаимно-однозначное • (биективное) соответствие Г = (X, Y, F)

14 • Биекция — это отображение, которое является одновременно и сюръективным, и инъективным. При биективном отображении каждому элементу одного множества соответствует ровно один элемент другого множества, при этом, определено обратное отображение, которое обладает тем же свойством. Поэтому биективное отображение называют ещё взаимно-однозначным отображением (соответствием), одно-однозначным отображением. • Если между двумя множествами можно установить взаимно-однозначное соответствие (биекция), то такие множества называются равномощными. С точки зрения теории множеств, равномощные множества неразличимы. • Взаимно-однозначное отображение конечного множества в себя называется перестановкой (элементов этого множества). (википедия)

Общее понятие функции • Пусть Х – некоторое числовое множество. • Говорят, что на Х задана функция, если любому элементу из множества Х поставлено в соответствие определенное число y Y. • Если теперь перейти от числовых множеств к множествам произвольной природы, то приходим к самому общему понятию ФУНКЦИИ.

17 • Пусть X и Y – множества произвольной природы, и пусть между ними задано соответствие. • Если соответствие функционально, то оно называется функцией и обозначается • f = (X, Y, F). • Из определения следует, что функция может быть определена не на всех элементах множества Х.

18 • Если же функция определена на всех элементах множества Х, т. е. введенное соответствие не только функциональное, но и всюду определенное, то такая функция называется ОТОБРАЖЕНИЕМ. • Различают отображение X на Y и отображение X в Y. • X на Y, если f(X) = Y, • X в Y, если f(X) Y. • ФУНКЦИЯ – частный вид СООТВЕТСТВИЯ.
12_22.11.pptx