Lecture 11.pptx
- Количество слайдов: 69
 Лекция 11 Фиктивные переменные
Лекция 11 Фиктивные переменные
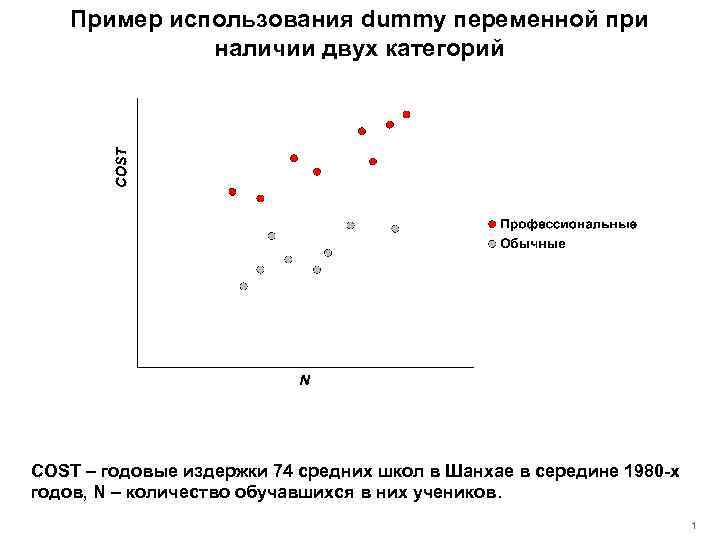 Пример использования dummy переменной при наличии двух категорий COST – годовые издержки 74 средних школ в Шанхае в середине 1980 -х годов, N – количество обучавшихся в них учеников. 1
Пример использования dummy переменной при наличии двух категорий COST – годовые издержки 74 средних школ в Шанхае в середине 1980 -х годов, N – количество обучавшихся в них учеников. 1
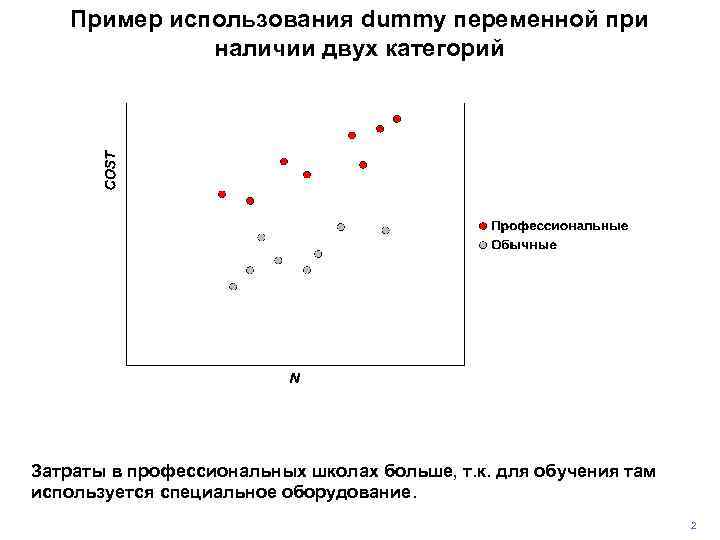 Пример использования dummy переменной при наличии двух категорий Затраты в профессиональных школах больше, т. к. для обучения там используется специальное оборудование. 2
Пример использования dummy переменной при наличии двух категорий Затраты в профессиональных школах больше, т. к. для обучения там используется специальное оборудование. 2
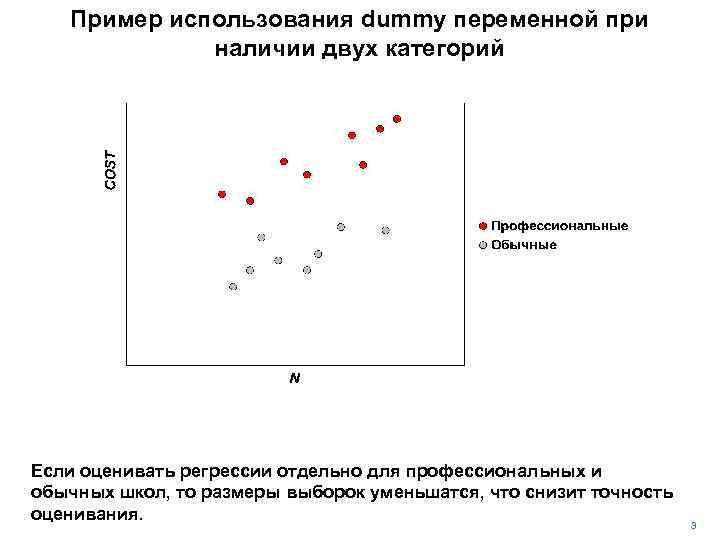 Пример использования dummy переменной при наличии двух категорий Если оценивать регрессии отдельно для профессиональных и обычных школ, то размеры выборок уменьшатся, что снизит точность оценивания. 3
Пример использования dummy переменной при наличии двух категорий Если оценивать регрессии отдельно для профессиональных и обычных школ, то размеры выборок уменьшатся, что снизит точность оценивания. 3
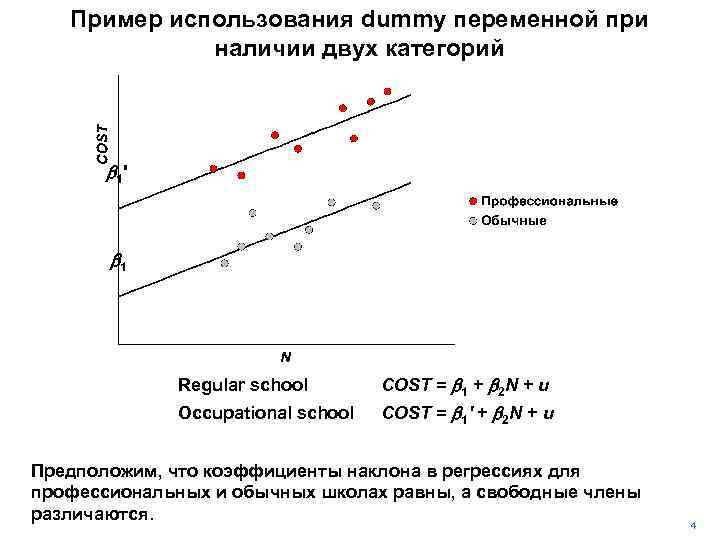 Пример использования dummy переменной при наличии двух категорий b 1 ' b 1 OCC = 0 Regular school COST = b 1 + b 2 N + u OCC = 1 Occupational school COST = b 1' + b 2 N + u Предположим, что коэффициенты наклона в регрессиях для профессиональных и обычных школах равны, а свободные члены различаются. 4
Пример использования dummy переменной при наличии двух категорий b 1 ' b 1 OCC = 0 Regular school COST = b 1 + b 2 N + u OCC = 1 Occupational school COST = b 1' + b 2 N + u Предположим, что коэффициенты наклона в регрессиях для профессиональных и обычных школах равны, а свободные члены различаются. 4
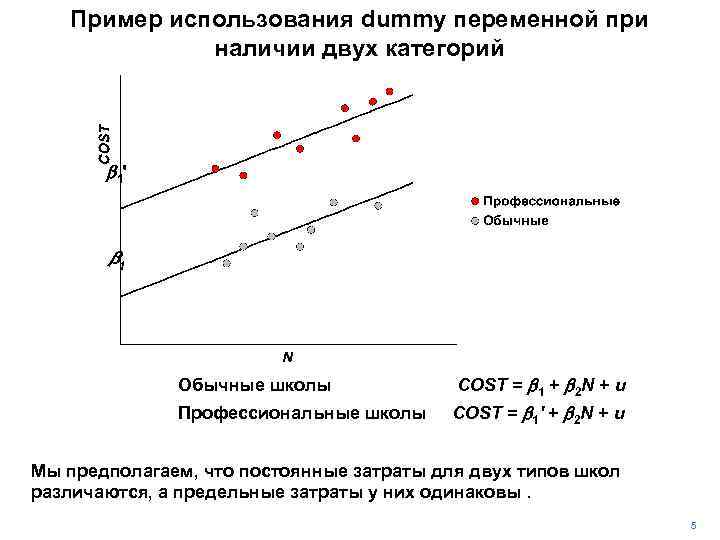 Пример использования dummy переменной при наличии двух категорий b 1' b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1' + b 2 N + u Мы предполагаем, что постоянные затраты для двух типов школ различаются, а предельные затраты у них одинаковы. 5
Пример использования dummy переменной при наличии двух категорий b 1' b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1' + b 2 N + u Мы предполагаем, что постоянные затраты для двух типов школ различаются, а предельные затраты у них одинаковы. 5
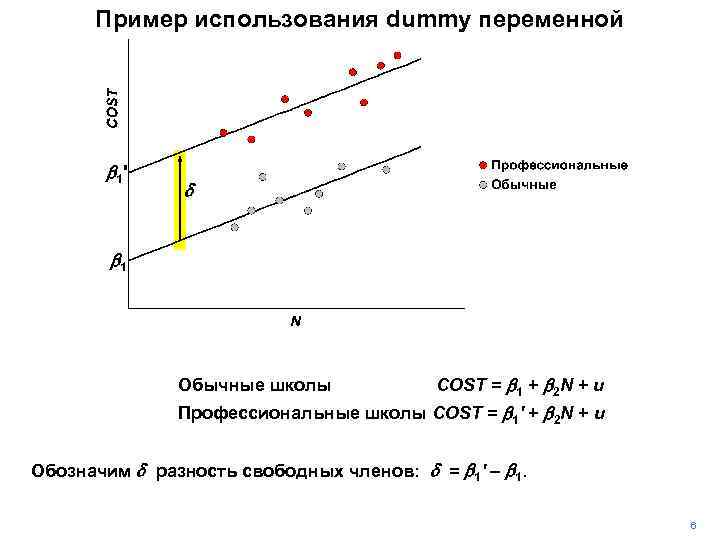 Пример использования dummy переменной b 1 ' d b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1' + b 2 N + u Обозначим d разность свободных членов: d = b 1' – b 1. 6
Пример использования dummy переменной b 1 ' d b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1' + b 2 N + u Обозначим d разность свободных членов: d = b 1' – b 1. 6
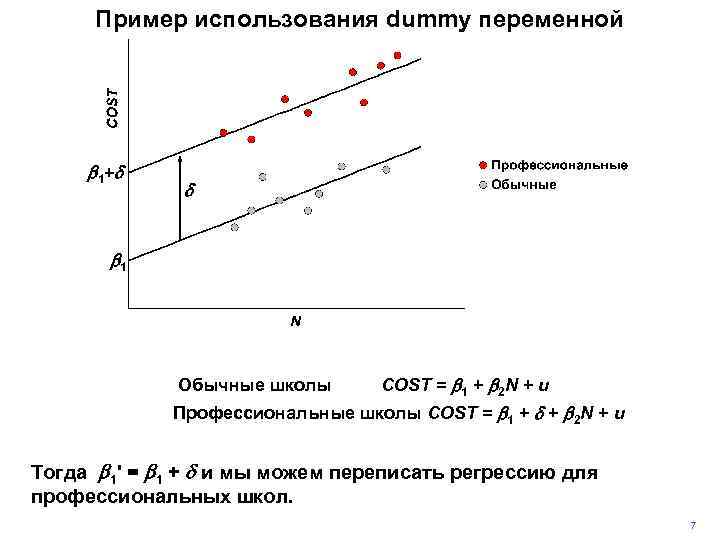 Пример использования dummy переменной b 1 +d d b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1 + d + b 2 N + u Тогда b 1' = b 1 + d и мы можем переписать регрессию для профессиональных школ. 7
Пример использования dummy переменной b 1 +d d b 1 OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы COST = b 1 + d + b 2 N + u Тогда b 1' = b 1 + d и мы можем переписать регрессию для профессиональных школ. 7
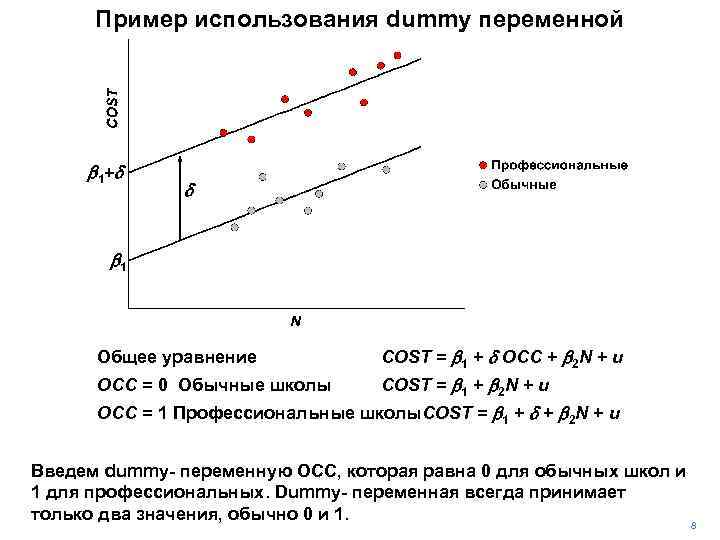 Пример использования dummy переменной b 1 +d d b 1 Общее уравнение COST = b 1 + d OCC + b 2 N + u OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы. COST = b 1 + d + b 2 N + u Введем dummy- переменную OCC, которая равна 0 для обычных школ и 1 для профессиональных. Dummy- переменная всегда принимает только два значения, обычно 0 и 1. 8
Пример использования dummy переменной b 1 +d d b 1 Общее уравнение COST = b 1 + d OCC + b 2 N + u OCC = 0 Обычные школы COST = b 1 + b 2 N + u OCC = 1 Профессиональные школы. COST = b 1 + d + b 2 N + u Введем dummy- переменную OCC, которая равна 0 для обычных школ и 1 для профессиональных. Dummy- переменная всегда принимает только два значения, обычно 0 и 1. 8
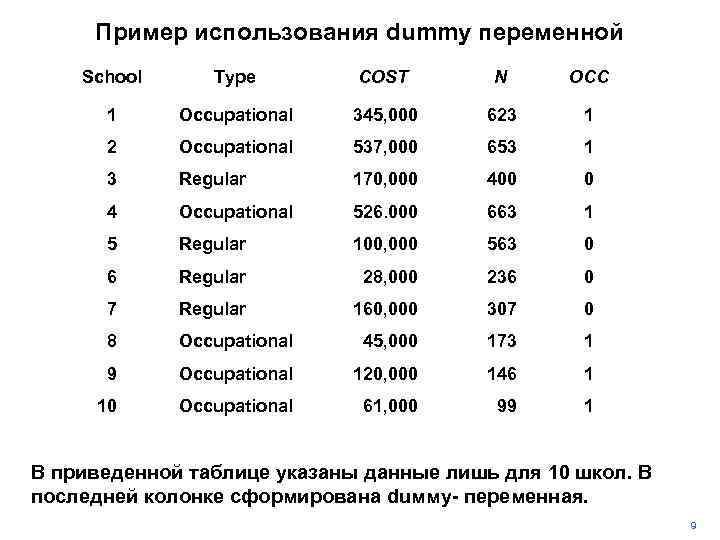 Пример использования dummy переменной School Type COST N OCC 1 Occupational 345, 000 623 1 2 Occupational 537, 000 653 1 3 Regular 170, 000 400 0 4 Occupational 526. 000 663 1 5 Regular 100, 000 563 0 6 Regular 28, 000 236 0 7 Regular 160, 000 307 0 8 Occupational 45, 000 173 1 9 Occupational 120, 000 146 1 10 Occupational 61, 000 99 1 В приведенной таблице указаны данные лишь для 10 школ. В последней колонке сформирована duммy- переменная. 9
Пример использования dummy переменной School Type COST N OCC 1 Occupational 345, 000 623 1 2 Occupational 537, 000 653 1 3 Regular 170, 000 400 0 4 Occupational 526. 000 663 1 5 Regular 100, 000 563 0 6 Regular 28, 000 236 0 7 Regular 160, 000 307 0 8 Occupational 45, 000 173 1 9 Occupational 120, 000 146 1 10 Occupational 61, 000 99 1 В приведенной таблице указаны данные лишь для 10 школ. В последней колонке сформирована duммy- переменная. 9
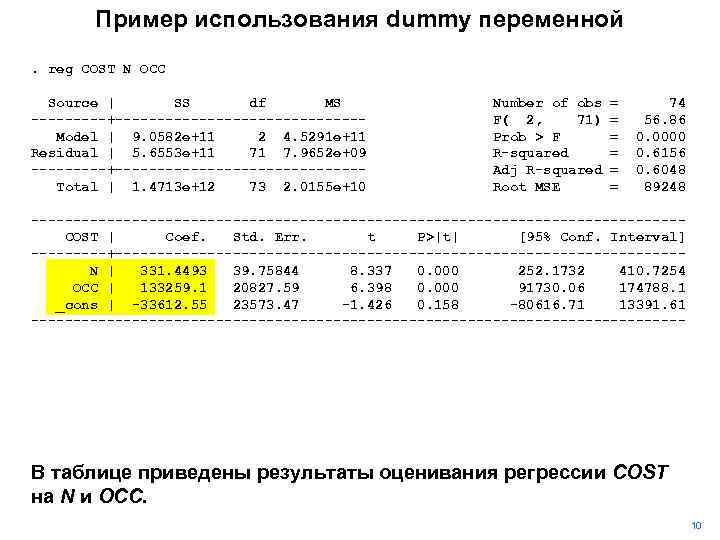 Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- В таблице приведены результаты оценивания регрессии COST на N и OCC. 10
Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- В таблице приведены результаты оценивания регрессии COST на N и OCC. 10
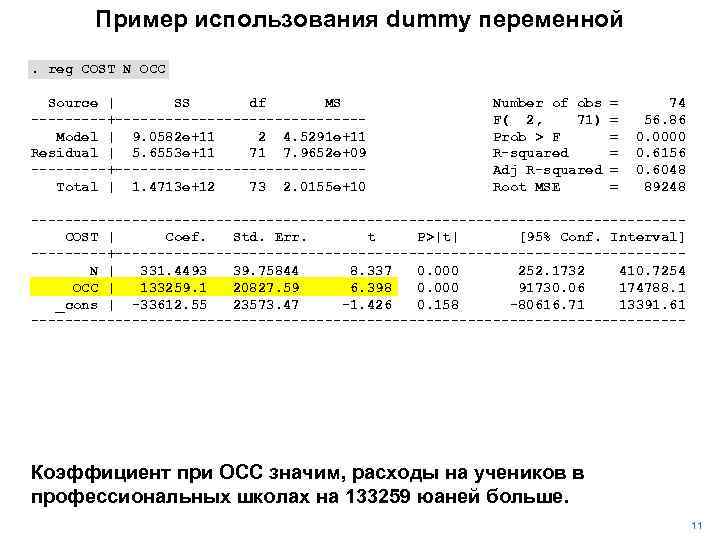 Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Коэффициент при OCC значим, расходы на учеников в профессиональных школах на 133259 юаней больше. 11
Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Коэффициент при OCC значим, расходы на учеников в профессиональных школах на 133259 юаней больше. 11
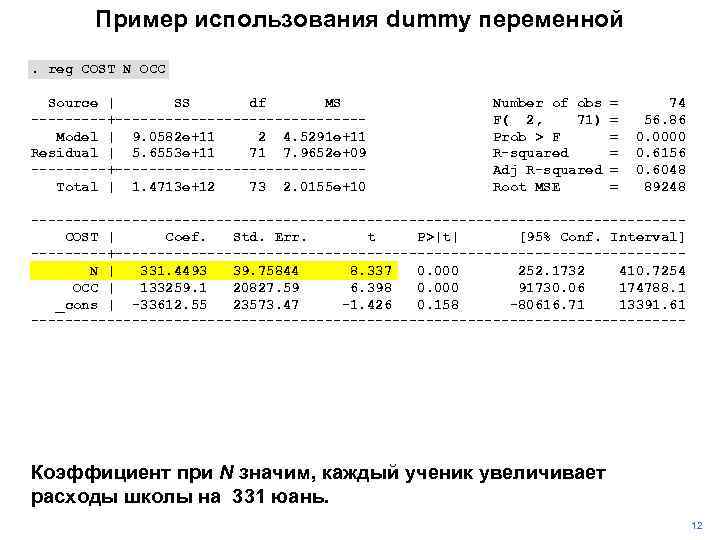 Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Коэффициент при N значим, каждый ученик увеличивает расходы школы на 331 юань. 12
Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Коэффициент при N значим, каждый ученик увеличивает расходы школы на 331 юань. 12
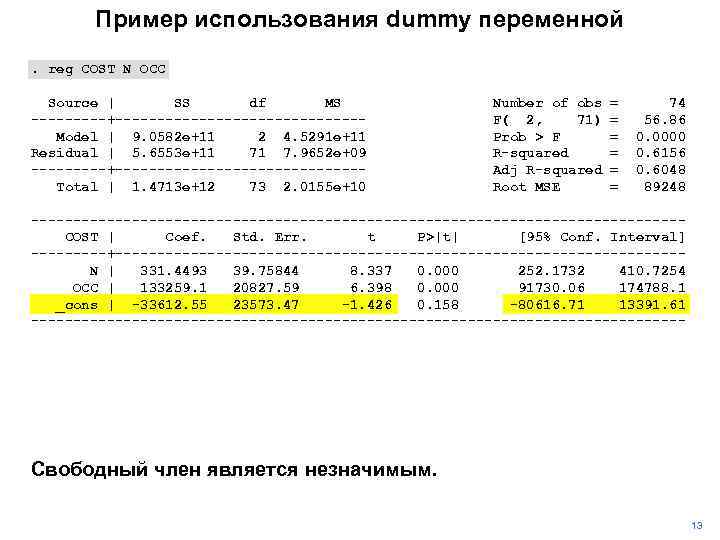 Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Свободный член является незначимым. 13
Пример использования dummy переменной. reg COST N OCC Source | SS df MS -----+---------------Model | 9. 0582 e+11 2 4. 5291 e+11 Residual | 5. 6553 e+11 71 7. 9652 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 2, 71) Prob > F R-squared Adj R-squared Root MSE = = = 74 56. 86 0. 0000 0. 6156 0. 6048 89248 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 331. 4493 39. 75844 8. 337 0. 000 252. 1732 410. 7254 OCC | 133259. 1 20827. 59 6. 398 0. 000 91730. 06 174788. 1 _cons | -33612. 55 23573. 47 -1. 426 0. 158 -80616. 71 13391. 61 --------------------------------------- Свободный член является незначимым. 13
 Несколько видов Dummy - переменных COST = b 1 + d OCC + e RES + b 2 N + u Dummy – переменная RES равна 1 для школ с проживанием и 0 для всех остальных. 1
Несколько видов Dummy - переменных COST = b 1 + d OCC + e RES + b 2 N + u Dummy – переменная RES равна 1 для школ с проживанием и 0 для всех остальных. 1
 Несколько видов Dummy - переменных COST = b 1 + d OCC + e RES + b 2 N + u Обычные, без проживания (OCC = RES = 0) Обычные, с проживанием (OCC = 0; RES = 1) COST = b 1 + b 2 N + u COST = (b 1 + e ) + b 2 N + u Профессиональные, без проживания (OCC = 1; RES = 0) Профессиональные, с проживанием (OCC = RES = 1) COST = (b 1 + d ) + b 2 N + u COST = (b 1 + d + e ) + b 2 N + u 2
Несколько видов Dummy - переменных COST = b 1 + d OCC + e RES + b 2 N + u Обычные, без проживания (OCC = RES = 0) Обычные, с проживанием (OCC = 0; RES = 1) COST = b 1 + b 2 N + u COST = (b 1 + e ) + b 2 N + u Профессиональные, без проживания (OCC = 1; RES = 0) Профессиональные, с проживанием (OCC = RES = 1) COST = (b 1 + d ) + b 2 N + u COST = (b 1 + d + e ) + b 2 N + u 2
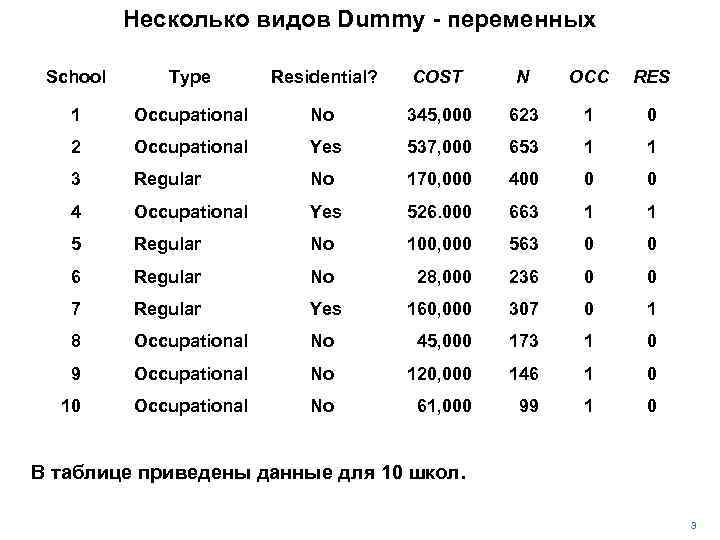 Несколько видов Dummy - переменных School Type Residential? COST N OCC RES 1 Occupational No 345, 000 623 1 0 2 Occupational Yes 537, 000 653 1 1 3 Regular No 170, 000 400 0 0 4 Occupational Yes 526. 000 663 1 1 5 Regular No 100, 000 563 0 0 6 Regular No 28, 000 236 0 0 7 Regular Yes 160, 000 307 0 1 8 Occupational No 45, 000 173 1 0 9 Occupational No 120, 000 146 1 0 10 Occupational No 61, 000 99 1 0 В таблице приведены данные для 10 школ. 3
Несколько видов Dummy - переменных School Type Residential? COST N OCC RES 1 Occupational No 345, 000 623 1 0 2 Occupational Yes 537, 000 653 1 1 3 Regular No 170, 000 400 0 0 4 Occupational Yes 526. 000 663 1 1 5 Regular No 100, 000 563 0 0 6 Regular No 28, 000 236 0 0 7 Regular Yes 160, 000 307 0 1 8 Occupational No 45, 000 173 1 0 9 Occupational No 120, 000 146 1 0 10 Occupational No 61, 000 99 1 0 В таблице приведены данные для 10 школ. 3
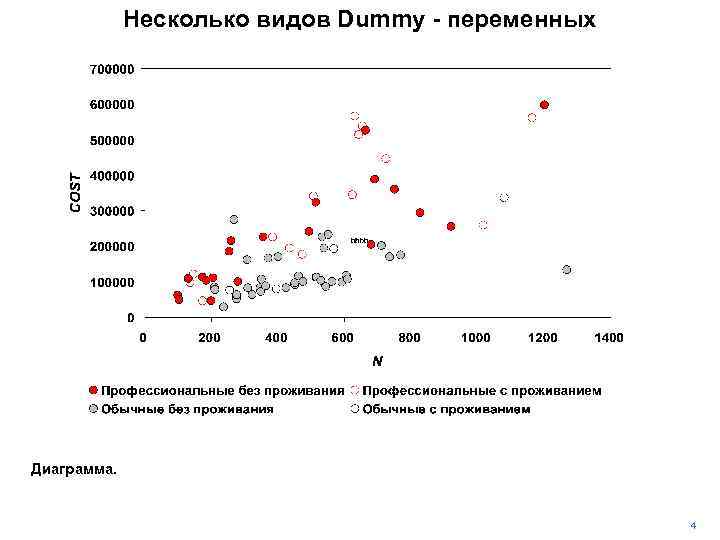 Несколько видов Dummy - переменных Диаграмма. 4
Несколько видов Dummy - переменных Диаграмма. 4
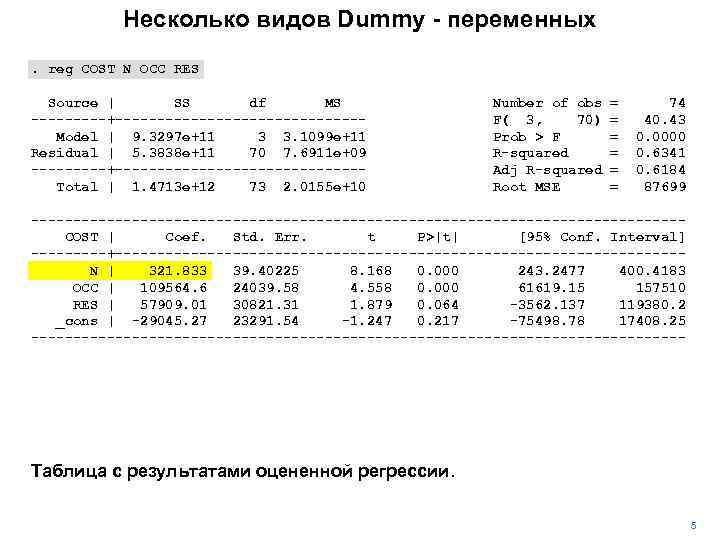 Несколько видов Dummy - переменных. reg COST N OCC RES Source | SS df MS -----+---------------Model | 9. 3297 e+11 3 3. 1099 e+11 Residual | 5. 3838 e+11 70 7. 6911 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 40. 43 0. 0000 0. 6341 0. 6184 87699 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 321. 833 39. 40225 8. 168 0. 000 243. 2477 400. 4183 OCC | 109564. 6 24039. 58 4. 558 0. 000 61619. 15 157510 RES | 57909. 01 30821. 31 1. 879 0. 064 -3562. 137 119380. 2 _cons | -29045. 27 23291. 54 -1. 247 0. 217 -75498. 78 17408. 25 --------------------------------------- Таблица с результатами оцененной регрессии. 5
Несколько видов Dummy - переменных. reg COST N OCC RES Source | SS df MS -----+---------------Model | 9. 3297 e+11 3 3. 1099 e+11 Residual | 5. 3838 e+11 70 7. 6911 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 40. 43 0. 0000 0. 6341 0. 6184 87699 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 321. 833 39. 40225 8. 168 0. 000 243. 2477 400. 4183 OCC | 109564. 6 24039. 58 4. 558 0. 000 61619. 15 157510 RES | 57909. 01 30821. 31 1. 879 0. 064 -3562. 137 119380. 2 _cons | -29045. 27 23291. 54 -1. 247 0. 217 -75498. 78 17408. 25 --------------------------------------- Таблица с результатами оцененной регрессии. 5
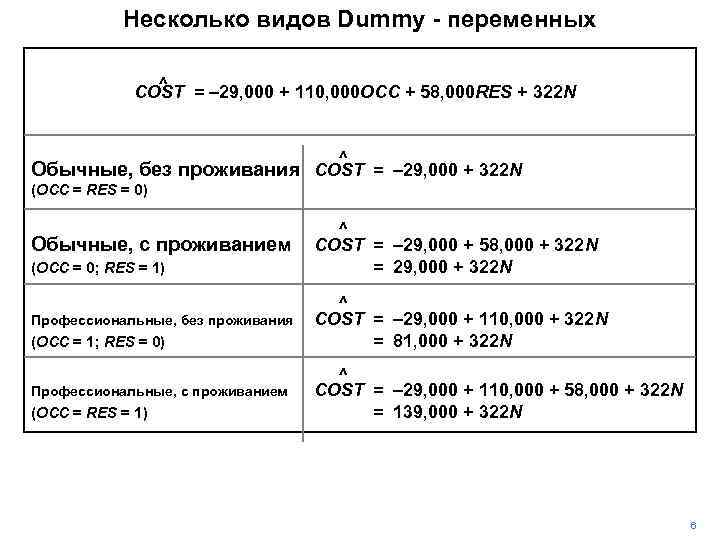 Несколько видов Dummy - переменных ^ COST = – 29, 000 + 110, 000 OCC + 58, 000 RES + 322 N ^ Обычные, без проживания COST = – 29, 000 + 322 N (OCC = RES = 0) Обычные, с проживанием (OCC = 0; RES = 1) Профессиональные, без проживания (OCC = 1; RES = 0) Профессиональные, с проживанием (OCC = RES = 1) ^ COST = – 29, 000 + 58, 000 + 322 N = 29, 000 + 322 N ^ COST = – 29, 000 + 110, 000 + 322 N = 81, 000 + 322 N ^ COST = – 29, 000 + 110, 000 + 58, 000 + 322 N = 139, 000 + 322 N 6
Несколько видов Dummy - переменных ^ COST = – 29, 000 + 110, 000 OCC + 58, 000 RES + 322 N ^ Обычные, без проживания COST = – 29, 000 + 322 N (OCC = RES = 0) Обычные, с проживанием (OCC = 0; RES = 1) Профессиональные, без проживания (OCC = 1; RES = 0) Профессиональные, с проживанием (OCC = RES = 1) ^ COST = – 29, 000 + 58, 000 + 322 N = 29, 000 + 322 N ^ COST = – 29, 000 + 110, 000 + 322 N = 81, 000 + 322 N ^ COST = – 29, 000 + 110, 000 + 58, 000 + 322 N = 139, 000 + 322 N 6
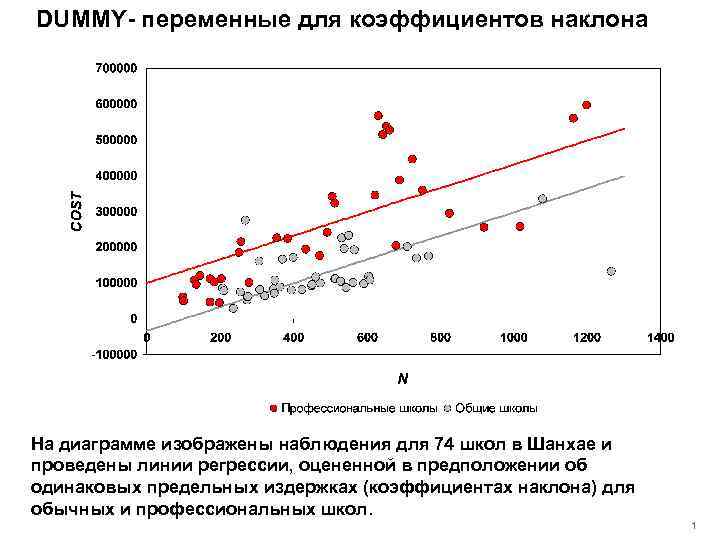 DUMMY- переменные для коэффициентов наклона На диаграмме изображены наблюдения для 74 школ в Шанхае и проведены линии регрессии, оцененной в предположении об одинаковых предельных издержках (коэффициентах наклона) для обычных и профессиональных школ. 1
DUMMY- переменные для коэффициентов наклона На диаграмме изображены наблюдения для 74 школ в Шанхае и проведены линии регрессии, оцененной в предположении об одинаковых предельных издержках (коэффициентах наклона) для обычных и профессиональных школ. 1
 DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Ослабим требование об одинаковых предельных издержках (коэффициентах наклона) для обычных и профессиональных школ. Введем переменную NOCC, произведение N и OCC. 2
DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Ослабим требование об одинаковых предельных издержках (коэффициентах наклона) для обычных и профессиональных школ. Введем переменную NOCC, произведение N и OCC. 2
 DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Обычные школы (OCC = NOCC = 0) COST = b 1 + b 2 N + u Для обычных школ переменная OCC равна 0 и, следовательно, NOCC также равна 0. 3
DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Обычные школы (OCC = NOCC = 0) COST = b 1 + b 2 N + u Для обычных школ переменная OCC равна 0 и, следовательно, NOCC также равна 0. 3
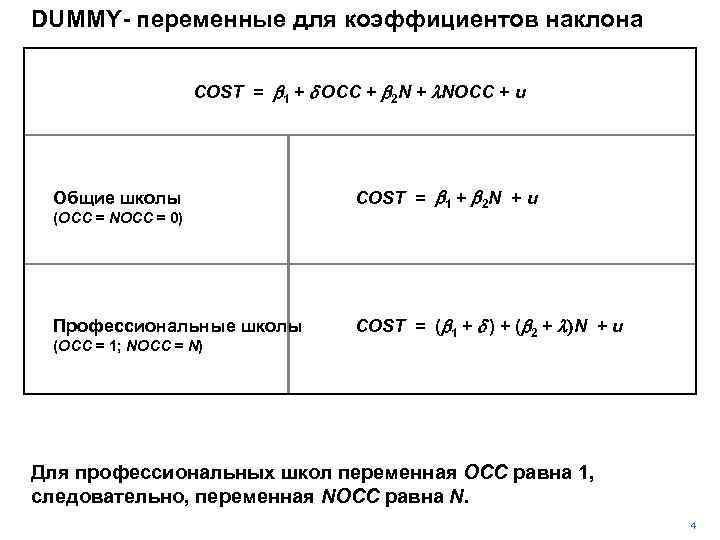 DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Общие школы (OCC = NOCC = 0) Профессиональные школы (OCC = 1; NOCC = N) COST = b 1 + b 2 N + u COST = (b 1 + d ) + (b 2 + l)N + u Для профессиональных школ переменная OCC равна 1, следовательно, переменная NOCC равна N. 4
DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Общие школы (OCC = NOCC = 0) Профессиональные школы (OCC = 1; NOCC = N) COST = b 1 + b 2 N + u COST = (b 1 + d ) + (b 2 + l)N + u Для профессиональных школ переменная OCC равна 1, следовательно, переменная NOCC равна N. 4
 DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Общие школы (OCC = NOCC = 0) Профессиональные школы (OCC = 1; NOCC = N) COST = b 1 + b 2 N + u COST = (b 1 + d ) + (b 2 + l)N + u Предельные издержки на одного студента профессиональной школы больше на l по сравнению с расходами на одного студента обыкновенной школы, постоянные издержки различаются на δ. 5
DUMMY- переменные для коэффициентов наклона COST = b 1 + d OCC + b 2 N + l. NOCC + u Общие школы (OCC = NOCC = 0) Профессиональные школы (OCC = 1; NOCC = N) COST = b 1 + b 2 N + u COST = (b 1 + d ) + (b 2 + l)N + u Предельные издержки на одного студента профессиональной школы больше на l по сравнению с расходами на одного студента обыкновенной школы, постоянные издержки различаются на δ. 5
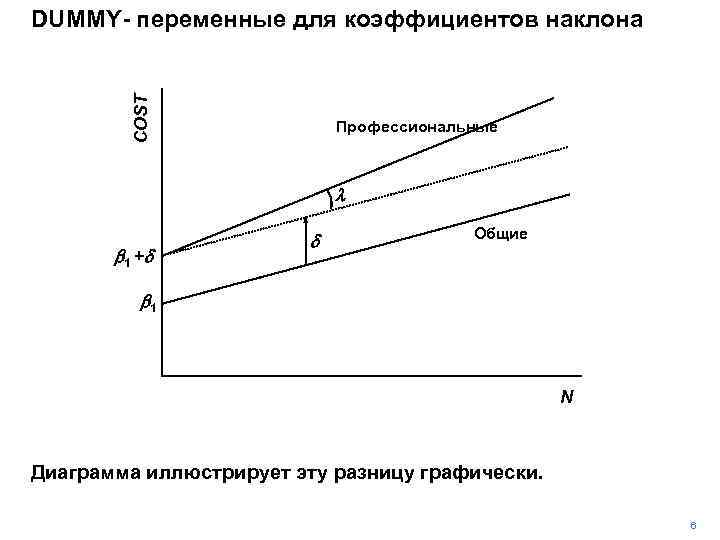 COST DUMMY- переменные для коэффициентов наклона Профессиональные l b 1 +d d Общие b 1 N Диаграмма иллюстрирует эту разницу графически. 6
COST DUMMY- переменные для коэффициентов наклона Профессиональные l b 1 +d d Общие b 1 N Диаграмма иллюстрирует эту разницу графически. 6
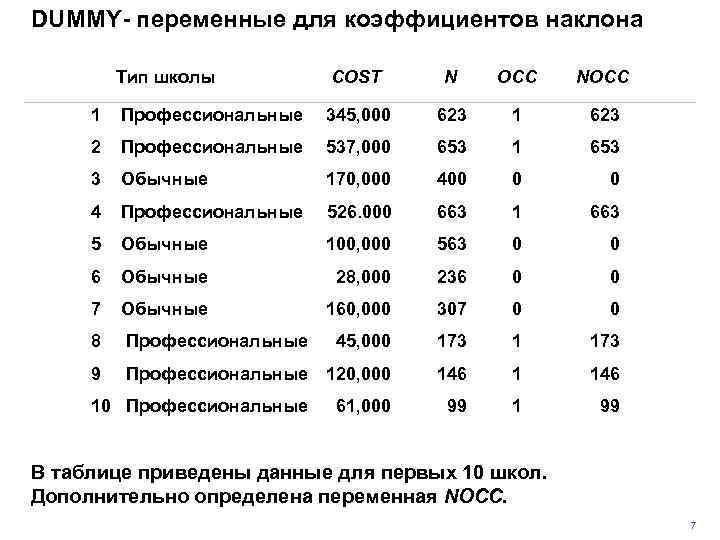 DUMMY- переменные для коэффициентов наклона Тип школы COST N OCC NOCC 1 Профессиональные 345, 000 623 1 623 2 Профессиональные 537, 000 653 1 653 3 Обычные 170, 000 400 0 0 4 Профессиональные 526. 000 663 1 663 5 Обычные 100, 000 563 0 0 6 Обычные 28, 000 236 0 0 7 Обычные 160, 000 307 0 0 8 Профессиональные 45, 000 173 1 173 9 Профессиональные 120, 000 146 1 146 99 10 Профессиональные 61, 000 В таблице приведены данные для первых 10 школ. Дополнительно определена переменная NOCC. 7
DUMMY- переменные для коэффициентов наклона Тип школы COST N OCC NOCC 1 Профессиональные 345, 000 623 1 623 2 Профессиональные 537, 000 653 1 653 3 Обычные 170, 000 400 0 0 4 Профессиональные 526. 000 663 1 663 5 Обычные 100, 000 563 0 0 6 Обычные 28, 000 236 0 0 7 Обычные 160, 000 307 0 0 8 Профессиональные 45, 000 173 1 173 9 Профессиональные 120, 000 146 1 146 99 10 Профессиональные 61, 000 В таблице приведены данные для первых 10 школ. Дополнительно определена переменная NOCC. 7
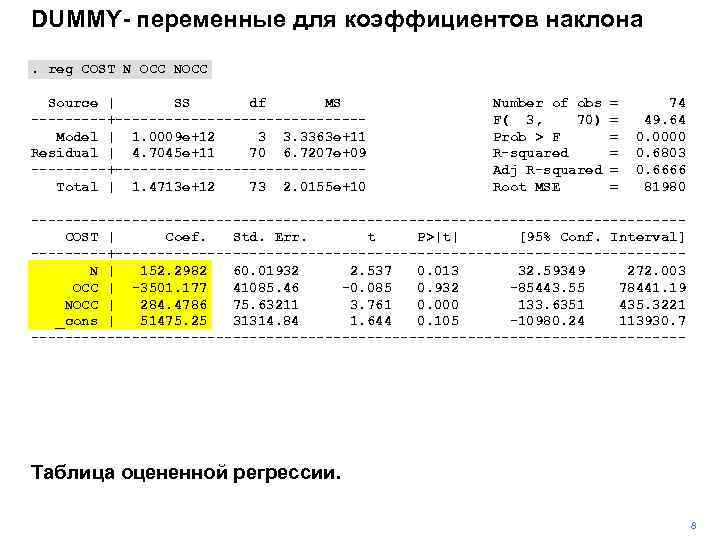 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Таблица оцененной регрессии. 8
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Таблица оцененной регрессии. 8
 DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Это уравнение оцененной регрессии. 9
DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Это уравнение оцененной регрессии. 9
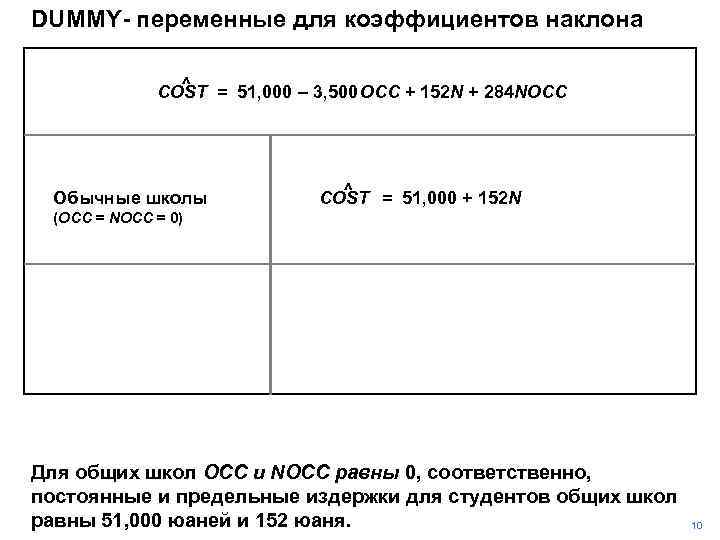 DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Обычные школы ^ COST = 51, 000 + 152 N (OCC = NOCC = 0) Для общих школ OCC и NOCC равны 0, соответственно, постоянные и предельные издержки для студентов общих школ равны 51, 000 юаней и 152 юаня. 10
DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Обычные школы ^ COST = 51, 000 + 152 N (OCC = NOCC = 0) Для общих школ OCC и NOCC равны 0, соответственно, постоянные и предельные издержки для студентов общих школ равны 51, 000 юаней и 152 юаня. 10
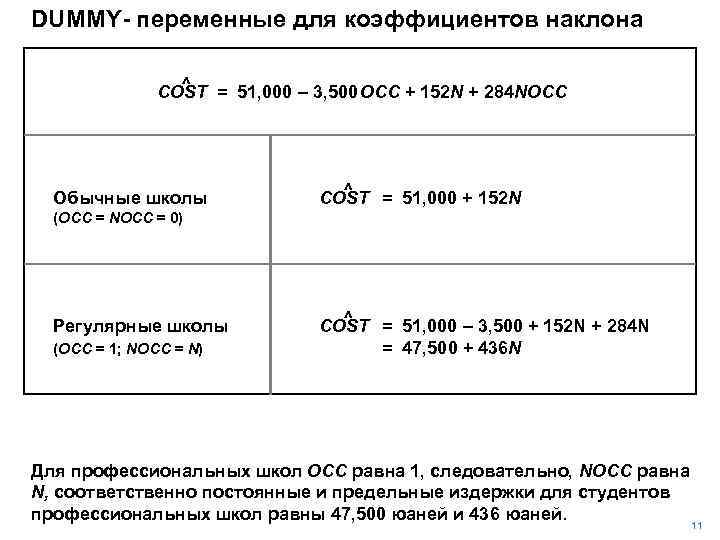 DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Обычные школы ^ COST = 51, 000 + 152 N (OCC = NOCC = 0) Регулярные школы (OCC = 1; NOCC = N) ^ COST = 51, 000 – 3, 500 + 152 N + 284 N = 47, 500 + 436 N Для профессиональных школ OCC равна 1, следовательно, NOCC равна N, соответственно постоянные и предельные издержки для студентов профессиональных школ равны 47, 500 юаней и 436 юаней. 11
DUMMY- переменные для коэффициентов наклона ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC Обычные школы ^ COST = 51, 000 + 152 N (OCC = NOCC = 0) Регулярные школы (OCC = 1; NOCC = N) ^ COST = 51, 000 – 3, 500 + 152 N + 284 N = 47, 500 + 436 N Для профессиональных школ OCC равна 1, следовательно, NOCC равна N, соответственно постоянные и предельные издержки для студентов профессиональных школ равны 47, 500 юаней и 436 юаней. 11
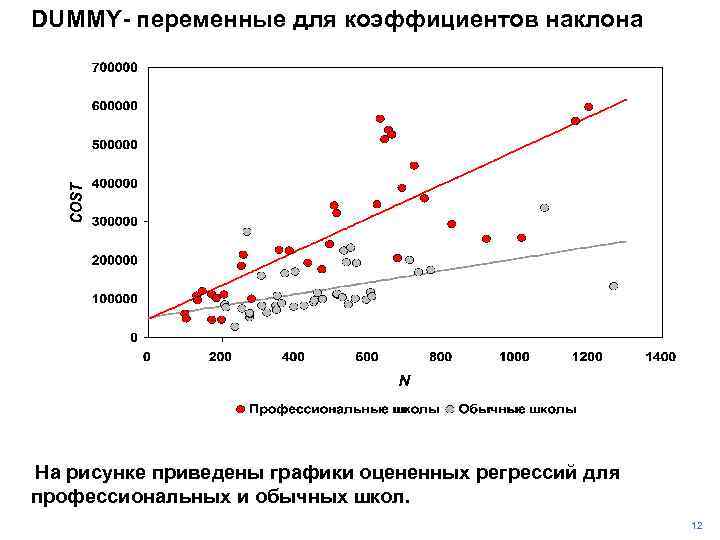 DUMMY- переменные для коэффициентов наклона На рисунке приведены графики оцененных регрессий для профессиональных и обычных школ. 12
DUMMY- переменные для коэффициентов наклона На рисунке приведены графики оцененных регрессий для профессиональных и обычных школ. 12
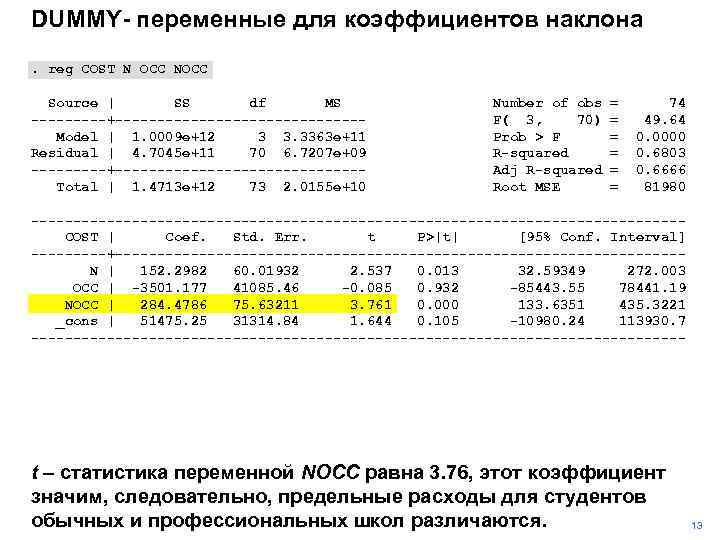 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- t – статистика переменной NOCC равна 3. 76, этот коэффициент значим, следовательно, предельные расходы для студентов обычных и профессиональных школ различаются. 13
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- t – статистика переменной NOCC равна 3. 76, этот коэффициент значим, следовательно, предельные расходы для студентов обычных и профессиональных школ различаются. 13
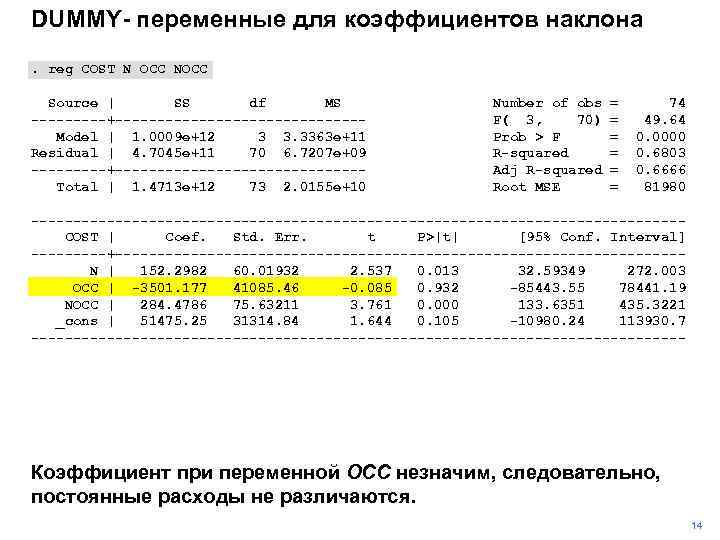 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Коэффициент при переменной OCC незначим, следовательно, постоянные расходы не различаются. 14
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Коэффициент при переменной OCC незначим, следовательно, постоянные расходы не различаются. 14
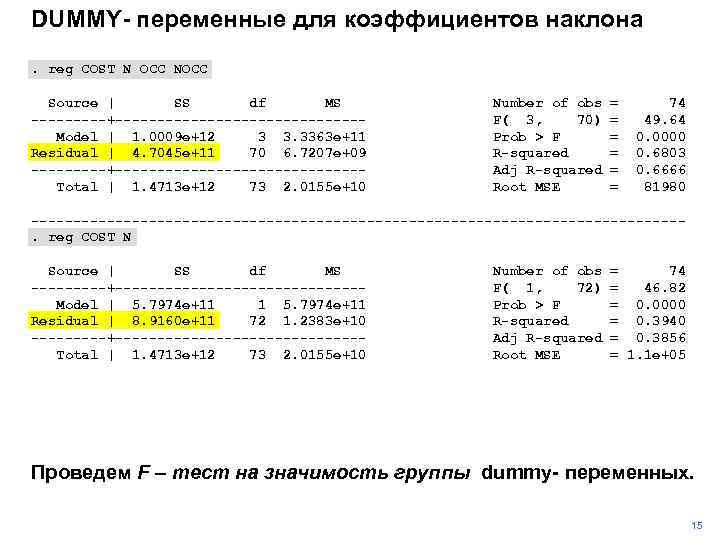 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Проведем F – тест на значимость группы dummy- переменных. 15
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Проведем F – тест на значимость группы dummy- переменных. 15
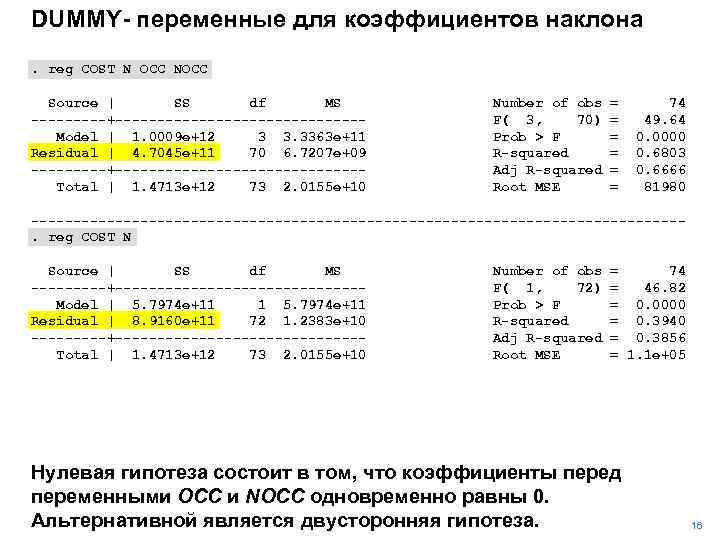 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Нулевая гипотеза состоит в том, что коэффициенты перед переменными OCC и NOCC одновременно равны 0. Альтернативной является двусторонняя гипотеза. 16
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Нулевая гипотеза состоит в том, что коэффициенты перед переменными OCC и NOCC одновременно равны 0. Альтернативной является двусторонняя гипотеза. 16
 DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Находим значение F – статистики и сравниваем его с критическим. Поскольку значение F- статистики больше критического (при любом разумном уровне значимости), то нулевая гипотеза отвергается. 17
DUMMY- переменные для коэффициентов наклона. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 Находим значение F – статистики и сравниваем его с критическим. Поскольку значение F- статистики больше критического (при любом разумном уровне значимости), то нулевая гипотеза отвергается. 17
 Сезонные dummy- переменные Часто в распоряжении исследователя имеются недельные, месячные или квартальные данные. Если качественная переменная имеет к градаций, то в модель надо ввести к – 1 фиктивных переменных. Например, если данные квартальные, то D 1 = 1, если наблюдение относится к 1 – му кварталу и 0, если не относится; D 2 = 1, если наблюдение относится к 2 – му кварталу и 0, если не относится; D 3 = 1, если наблюдение относится к 3 – му кварталу и 0, если не относится; 1
Сезонные dummy- переменные Часто в распоряжении исследователя имеются недельные, месячные или квартальные данные. Если качественная переменная имеет к градаций, то в модель надо ввести к – 1 фиктивных переменных. Например, если данные квартальные, то D 1 = 1, если наблюдение относится к 1 – му кварталу и 0, если не относится; D 2 = 1, если наблюдение относится к 2 – му кварталу и 0, если не относится; D 3 = 1, если наблюдение относится к 3 – му кварталу и 0, если не относится; 1
 Сезонные dummy- переменные Модель: Y = β 0 + β 1 D 1 + β 2 D 2 + β 3 D 3 + β 4 X + u Оцененное уравнение регрессии: ^ Y = b 0 + b 1 D 1 + b 2 D 2 + b 3 D 3 + b 4 X Поквартальные зависимости: ^ Y = b 0 + b 1 D 1 + b 4 X - для 1 -го квартала, ^ Y = b 0 + b 2 D 2 + b 4 X - для 2 -го квартала, ^ Y = b 0 + b 3 D 3 + b 4 X - для 3 -го квартала, ^ Y = b 0 + b 4 X - для 4 -го квартала (базового). 1
Сезонные dummy- переменные Модель: Y = β 0 + β 1 D 1 + β 2 D 2 + β 3 D 3 + β 4 X + u Оцененное уравнение регрессии: ^ Y = b 0 + b 1 D 1 + b 2 D 2 + b 3 D 3 + b 4 X Поквартальные зависимости: ^ Y = b 0 + b 1 D 1 + b 4 X - для 1 -го квартала, ^ Y = b 0 + b 2 D 2 + b 4 X - для 2 -го квартала, ^ Y = b 0 + b 3 D 3 + b 4 X - для 3 -го квартала, ^ Y = b 0 + b 4 X - для 4 -го квартала (базового). 1
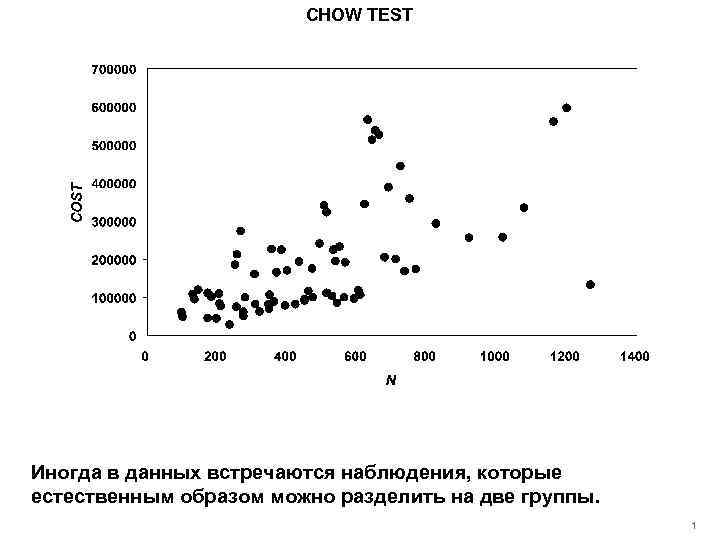 CHOW TEST Иногда в данных встречаются наблюдения, которые естественным образом можно разделить на две группы. 1
CHOW TEST Иногда в данных встречаются наблюдения, которые естественным образом можно разделить на две группы. 1
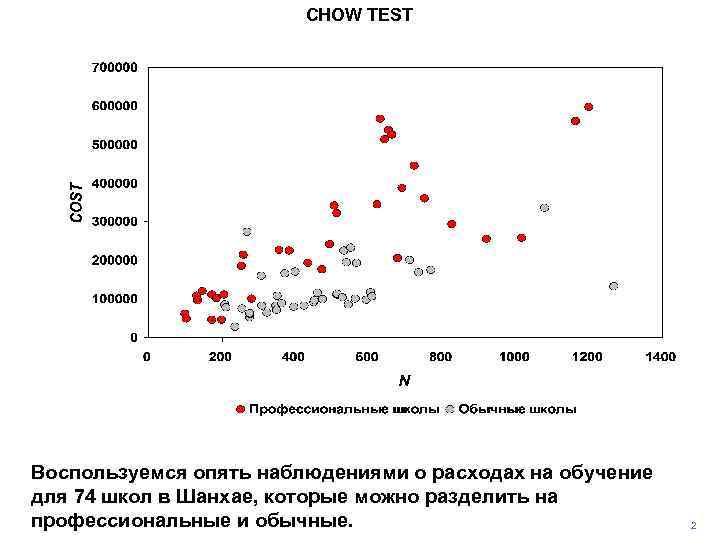 CHOW TEST Воспользуемся опять наблюдениями о расходах на обучение для 74 школ в Шанхае, которые можно разделить на профессиональные и обычные. 2
CHOW TEST Воспользуемся опять наблюдениями о расходах на обучение для 74 школ в Шанхае, которые можно разделить на профессиональные и обычные. 2
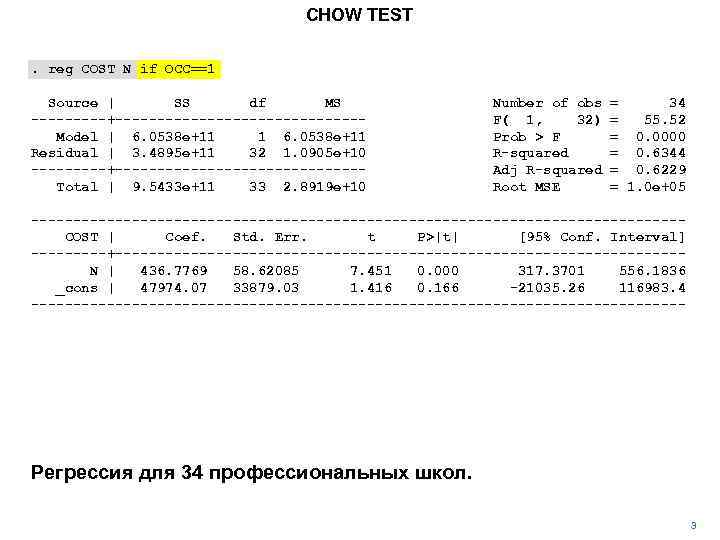 CHOW TEST. reg COST N if OCC==1 Source | SS df MS -----+---------------Model | 6. 0538 e+11 1 6. 0538 e+11 Residual | 3. 4895 e+11 32 1. 0905 e+10 -----+---------------Total | 9. 5433 e+11 33 2. 8919 e+10 Number of obs F( 1, 32) Prob > F R-squared Adj R-squared Root MSE = 34 = 55. 52 = 0. 0000 = 0. 6344 = 0. 6229 = 1. 0 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 436. 7769 58. 62085 7. 451 0. 000 317. 3701 556. 1836 _cons | 47974. 07 33879. 03 1. 416 0. 166 -21035. 26 116983. 4 --------------------------------------- Регрессия для 34 профессиональных школ. 3
CHOW TEST. reg COST N if OCC==1 Source | SS df MS -----+---------------Model | 6. 0538 e+11 1 6. 0538 e+11 Residual | 3. 4895 e+11 32 1. 0905 e+10 -----+---------------Total | 9. 5433 e+11 33 2. 8919 e+10 Number of obs F( 1, 32) Prob > F R-squared Adj R-squared Root MSE = 34 = 55. 52 = 0. 0000 = 0. 6344 = 0. 6229 = 1. 0 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 436. 7769 58. 62085 7. 451 0. 000 317. 3701 556. 1836 _cons | 47974. 07 33879. 03 1. 416 0. 166 -21035. 26 116983. 4 --------------------------------------- Регрессия для 34 профессиональных школ. 3
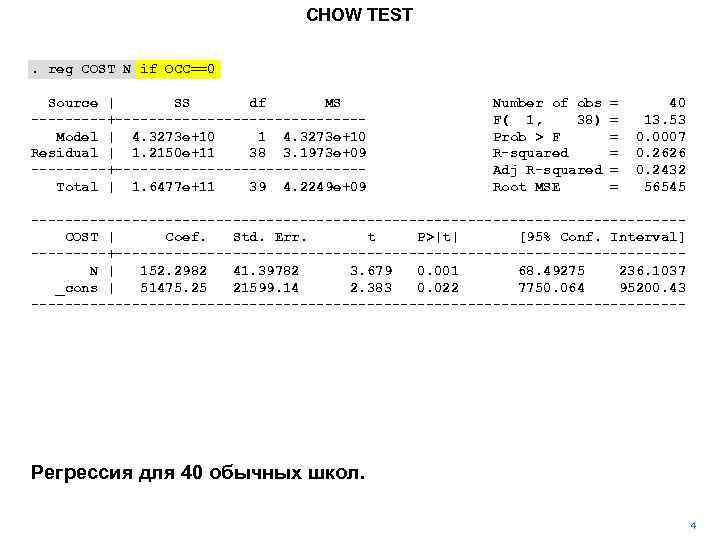 CHOW TEST. reg COST N if OCC==0 Source | SS df MS -----+---------------Model | 4. 3273 e+10 1 4. 3273 e+10 Residual | 1. 2150 e+11 38 3. 1973 e+09 -----+---------------Total | 1. 6477 e+11 39 4. 2249 e+09 Number of obs F( 1, 38) Prob > F R-squared Adj R-squared Root MSE = = = 40 13. 53 0. 0007 0. 2626 0. 2432 56545 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 41. 39782 3. 679 0. 001 68. 49275 236. 1037 _cons | 51475. 25 21599. 14 2. 383 0. 022 7750. 064 95200. 43 --------------------------------------- Регрессия для 40 обычных школ. 4
CHOW TEST. reg COST N if OCC==0 Source | SS df MS -----+---------------Model | 4. 3273 e+10 1 4. 3273 e+10 Residual | 1. 2150 e+11 38 3. 1973 e+09 -----+---------------Total | 1. 6477 e+11 39 4. 2249 e+09 Number of obs F( 1, 38) Prob > F R-squared Adj R-squared Root MSE = = = 40 13. 53 0. 0007 0. 2626 0. 2432 56545 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 41. 39782 3. 679 0. 001 68. 49275 236. 1037 _cons | 51475. 25 21599. 14 2. 383 0. 022 7750. 064 95200. 43 --------------------------------------- Регрессия для 40 обычных школ. 4
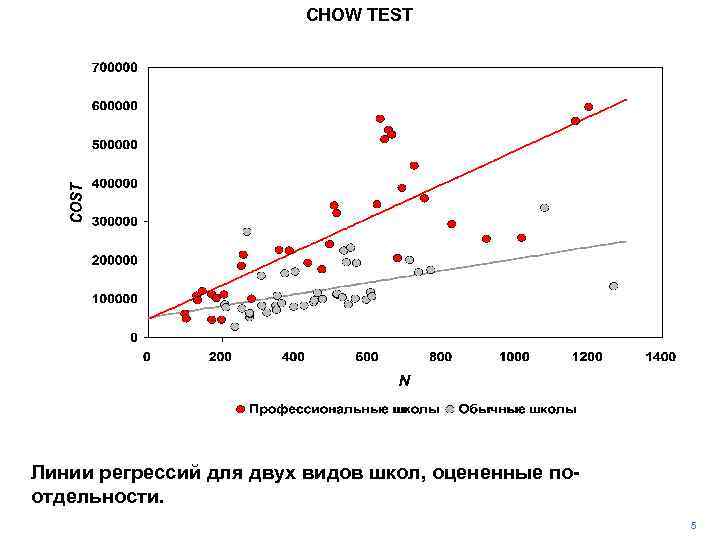 CHOW TEST Линии регрессий для двух видов школ, оцененные поотдельности. 5
CHOW TEST Линии регрессий для двух видов школ, оцененные поотдельности. 5
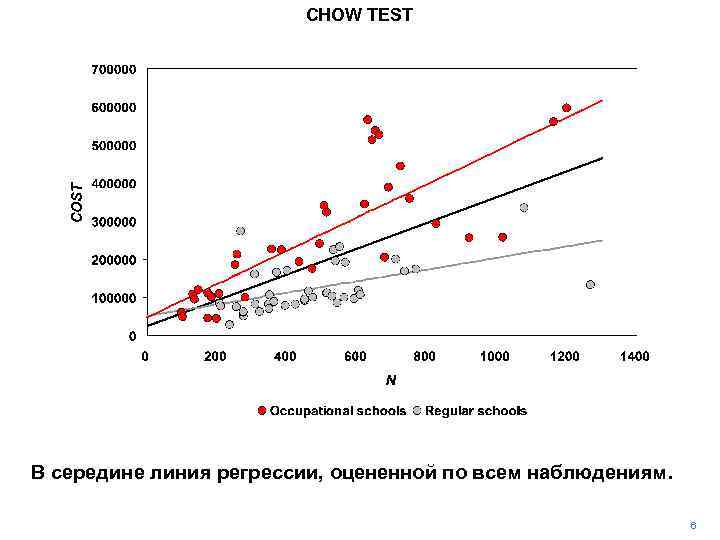 CHOW TEST В середине линия регрессии, оцененной по всем наблюдениям. 6
CHOW TEST В середине линия регрессии, оцененной по всем наблюдениям. 6
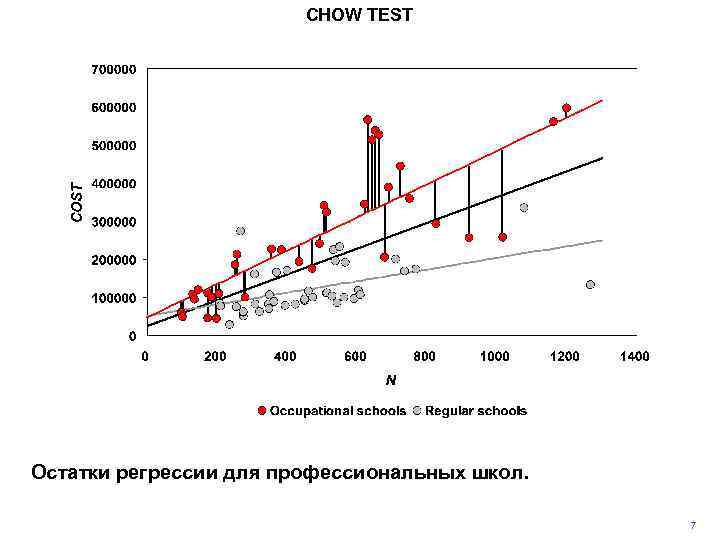 CHOW TEST Остатки регрессии для профессиональных школ. 7
CHOW TEST Остатки регрессии для профессиональных школ. 7
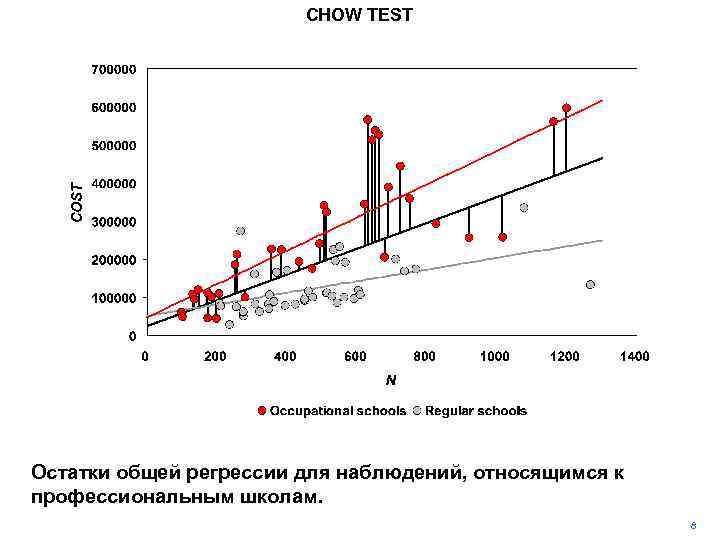 CHOW TEST Остатки общей регрессии для наблюдений, относящимся к профессиональным школам. 8
CHOW TEST Остатки общей регрессии для наблюдений, относящимся к профессиональным школам. 8
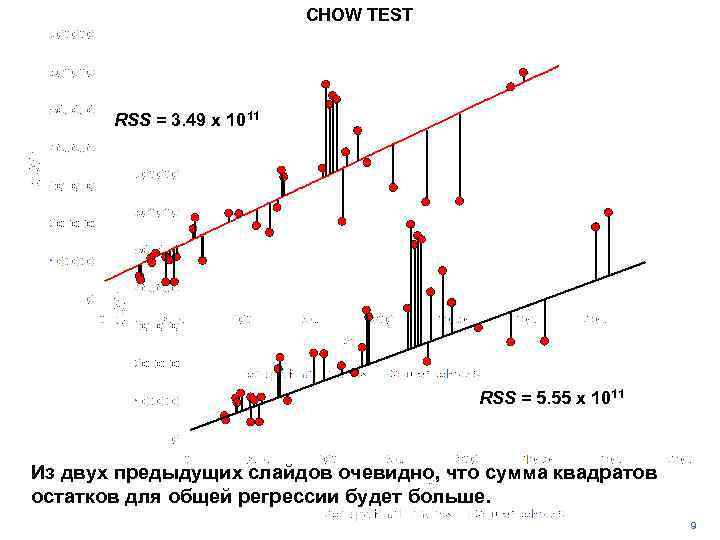 CHOW TEST RSS = 3. 49 x 1011 RSS = 5. 55 x 1011 Из двух предыдущих слайдов очевидно, что сумма квадратов остатков для общей регрессии будет больше. 9
CHOW TEST RSS = 3. 49 x 1011 RSS = 5. 55 x 1011 Из двух предыдущих слайдов очевидно, что сумма квадратов остатков для общей регрессии будет больше. 9
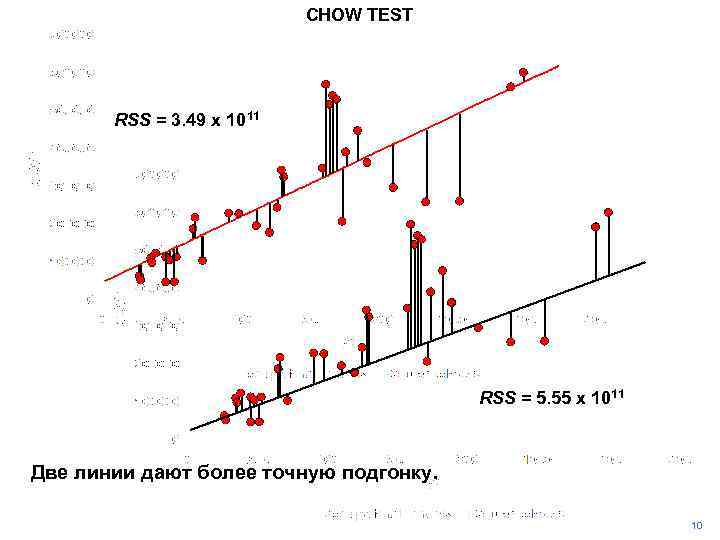 CHOW TEST RSS = 3. 49 x 1011 RSS = 5. 55 x 1011 Две линии дают более точную подгонку. 10
CHOW TEST RSS = 3. 49 x 1011 RSS = 5. 55 x 1011 Две линии дают более точную подгонку. 10
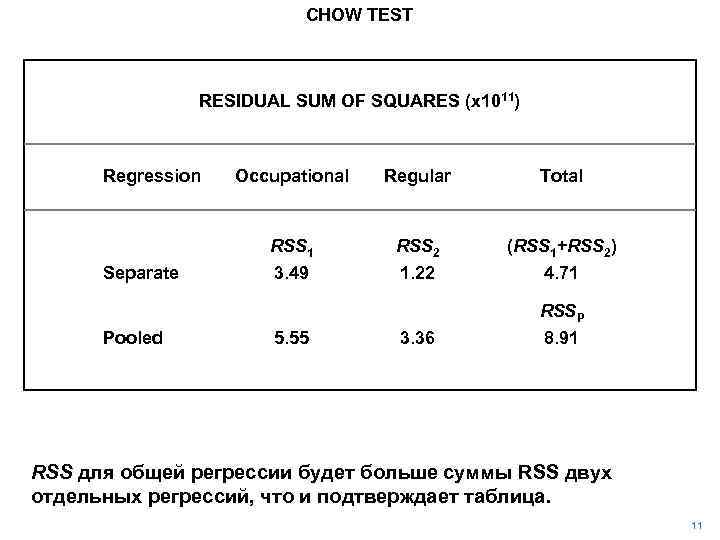 CHOW TEST RESIDUAL SUM OF SQUARES (x 1011) Regression Separate Occupational Regular Total RSS 1 3. 49 RSS 2 1. 22 (RSS 1+RSS 2) 4. 71 RSSP Pooled 5. 55 3. 36 8. 91 RSS для общей регрессии будет больше суммы RSS двух отдельных регрессий, что и подтверждает таблица. 11
CHOW TEST RESIDUAL SUM OF SQUARES (x 1011) Regression Separate Occupational Regular Total RSS 1 3. 49 RSS 2 1. 22 (RSS 1+RSS 2) 4. 71 RSSP Pooled 5. 55 3. 36 8. 91 RSS для общей регрессии будет больше суммы RSS двух отдельных регрессий, что и подтверждает таблица. 11
 CHOW TEST Тест Chow дает ответ на вопрос, можно ли считать что две выборки принадлежат одной генеральной совокупности, т. е. лучше оценивать одну регрессию, или к разным, тогда лучше оценивать две отдельные регрессии. 12
CHOW TEST Тест Chow дает ответ на вопрос, можно ли считать что две выборки принадлежат одной генеральной совокупности, т. е. лучше оценивать одну регрессию, или к разным, тогда лучше оценивать две отдельные регрессии. 12
 Основная и альтернативная гипотезы в тесте Chow Модель для первого набора наблюдений: Модель для второго Набора наблюдений: 13
Основная и альтернативная гипотезы в тесте Chow Модель для первого набора наблюдений: Модель для второго Набора наблюдений: 13
 Тестовая статистика в тесте Chow Если F > Fcr (при выбранном уровне значимости), то основная гипотеза отвергается. 14
Тестовая статистика в тесте Chow Если F > Fcr (при выбранном уровне значимости), то основная гипотеза отвергается. 14
 CHOW TEST F(k, n – 2 k) = (RSS 1+RSS 2) 4. 71 RSSP 8. 91 Вернемся к рассматриваемому примеру. 15
CHOW TEST F(k, n – 2 k) = (RSS 1+RSS 2) 4. 71 RSSP 8. 91 Вернемся к рассматриваемому примеру. 15
 CHOW TEST F(k, n – 2 k) = Полученное значение F- статистики превышает критическое при любом разумном уровне значимости, следовательно, нулевая гипотеза отвергается, для профессиональных и обычных школ имеет место разная зависимость. 16
CHOW TEST F(k, n – 2 k) = Полученное значение F- статистики превышает критическое при любом разумном уровне значимости, следовательно, нулевая гипотеза отвергается, для профессиональных и обычных школ имеет место разная зависимость. 16
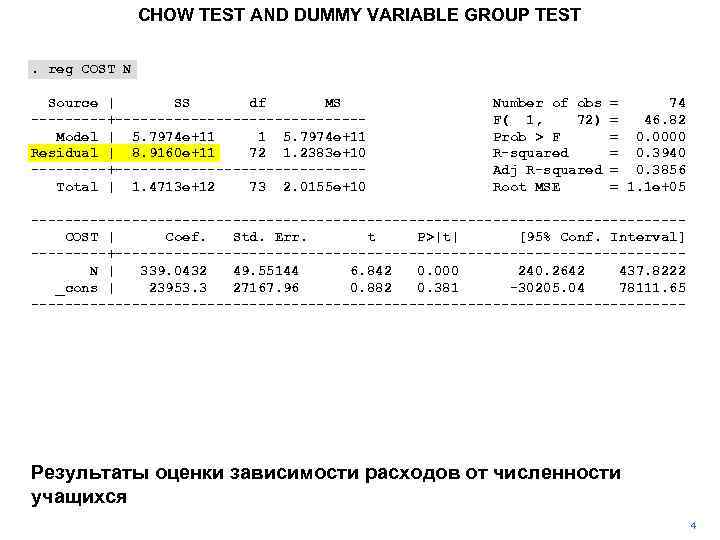 CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 339. 0432 49. 55144 6. 842 0. 000 240. 2642 437. 8222 _cons | 23953. 3 27167. 96 0. 882 0. 381 -30205. 04 78111. 65 --------------------------------------- Результаты оценки зависимости расходов от численности учащихся 4
CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N Source | SS df MS -----+---------------Model | 5. 7974 e+11 1 5. 7974 e+11 Residual | 8. 9160 e+11 72 1. 2383 e+10 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 1, 72) Prob > F R-squared Adj R-squared Root MSE = 74 = 46. 82 = 0. 0000 = 0. 3940 = 0. 3856 = 1. 1 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 339. 0432 49. 55144 6. 842 0. 000 240. 2642 437. 8222 _cons | 23953. 3 27167. 96 0. 882 0. 381 -30205. 04 78111. 65 --------------------------------------- Результаты оценки зависимости расходов от численности учащихся 4
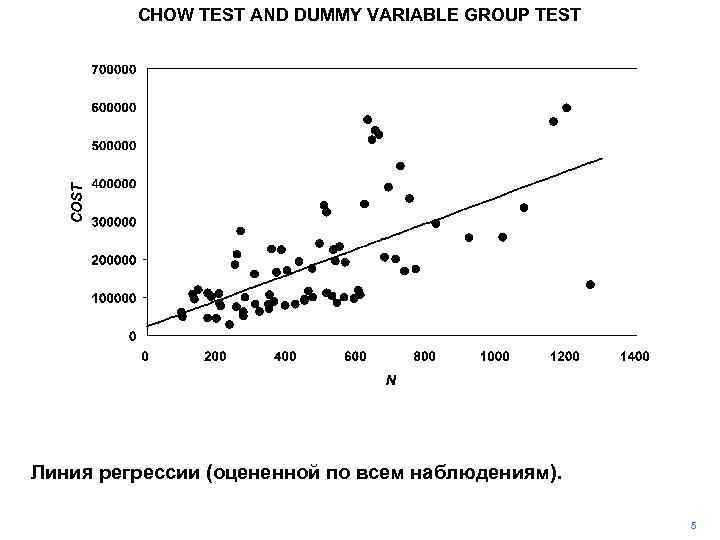 CHOW TEST AND DUMMY VARIABLE GROUP TEST Линия регрессии (оцененной по всем наблюдениям). 5
CHOW TEST AND DUMMY VARIABLE GROUP TEST Линия регрессии (оцененной по всем наблюдениям). 5
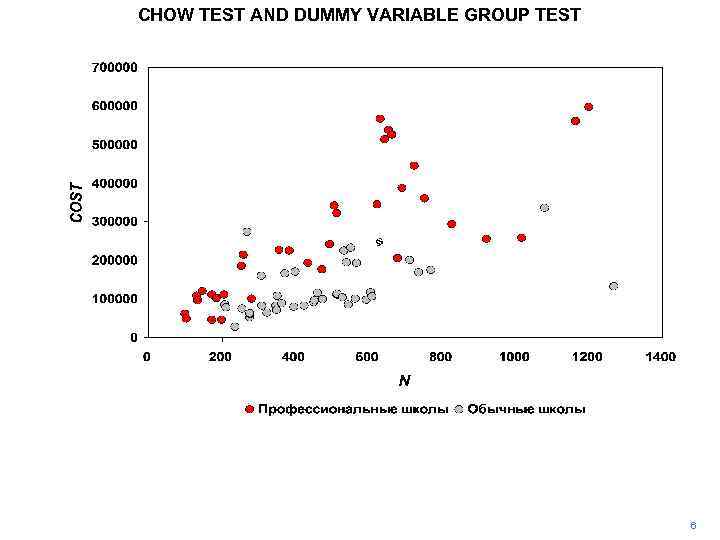 CHOW TEST AND DUMMY VARIABLE GROUP TEST 6
CHOW TEST AND DUMMY VARIABLE GROUP TEST 6
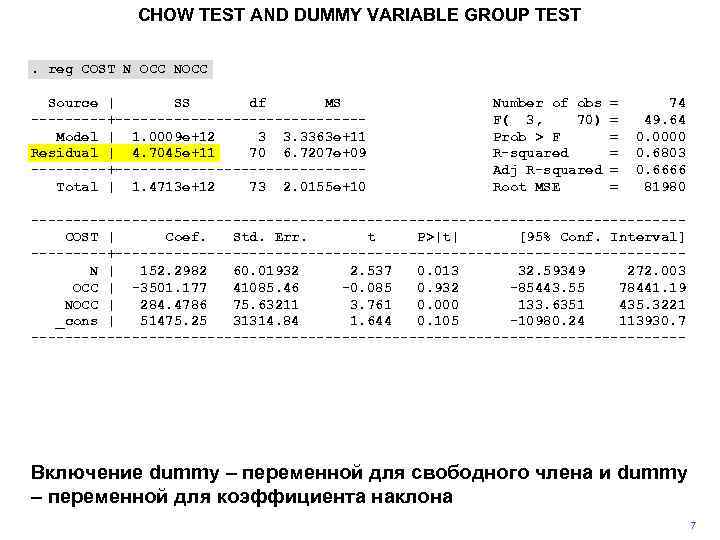 CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Включение dummy – переменной для свободного члена и dummy – переменной для коэффициента наклона 7
CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N OCC NOCC Source | SS df MS -----+---------------Model | 1. 0009 e+12 3 3. 3363 e+11 Residual | 4. 7045 e+11 70 6. 7207 e+09 -----+---------------Total | 1. 4713 e+12 73 2. 0155 e+10 Number of obs F( 3, 70) Prob > F R-squared Adj R-squared Root MSE = = = 74 49. 64 0. 0000 0. 6803 0. 6666 81980 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 60. 01932 2. 537 0. 013 32. 59349 272. 003 OCC | -3501. 177 41085. 46 -0. 085 0. 932 -85443. 55 78441. 19 NOCC | 284. 4786 75. 63211 3. 761 0. 000 133. 6351 435. 3221 _cons | 51475. 25 31314. 84 1. 644 0. 105 -10980. 24 113930. 7 --------------------------------------- Включение dummy – переменной для свободного члена и dummy – переменной для коэффициента наклона 7
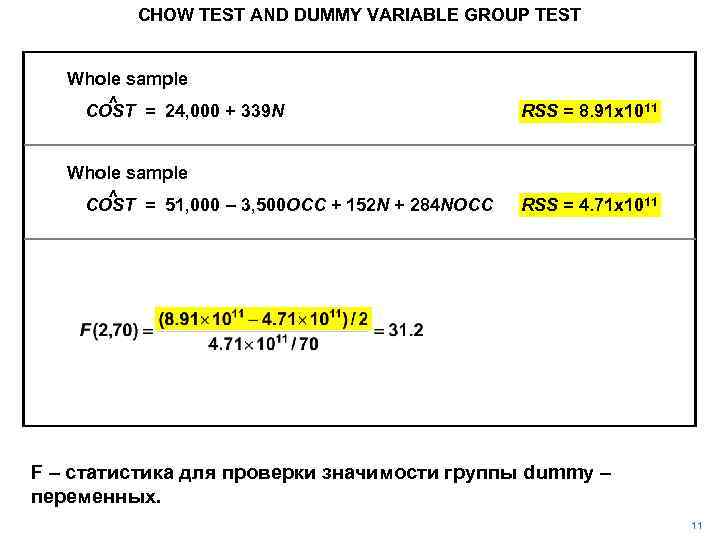 CHOW TEST AND DUMMY VARIABLE GROUP TEST Whole sample ^ COST = 24, 000 + 339 N RSS = 8. 91 x 1011 Whole sample ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 F – статистика для проверки значимости группы dummy – переменных. 11
CHOW TEST AND DUMMY VARIABLE GROUP TEST Whole sample ^ COST = 24, 000 + 339 N RSS = 8. 91 x 1011 Whole sample ^ COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 F – статистика для проверки значимости группы dummy – переменных. 11
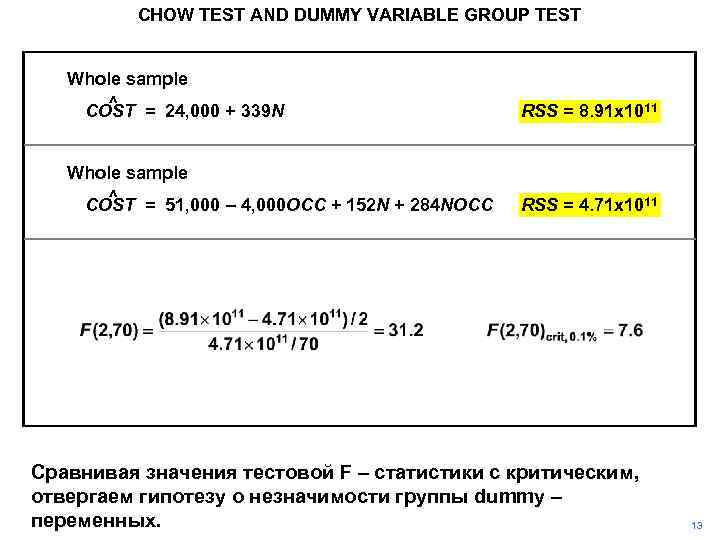 CHOW TEST AND DUMMY VARIABLE GROUP TEST Whole sample ^ COST = 24, 000 + 339 N RSS = 8. 91 x 1011 Whole sample ^ COST = 51, 000 – 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 Сравнивая значения тестовой F – статистики с критическим, отвергаем гипотезу о незначимости группы dummy – переменных. 13
CHOW TEST AND DUMMY VARIABLE GROUP TEST Whole sample ^ COST = 24, 000 + 339 N RSS = 8. 91 x 1011 Whole sample ^ COST = 51, 000 – 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 Сравнивая значения тестовой F – статистики с критическим, отвергаем гипотезу о незначимости группы dummy – переменных. 13
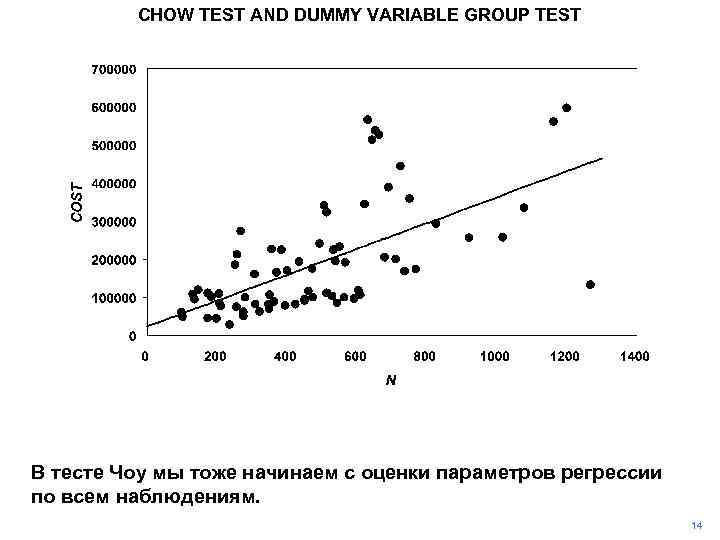 CHOW TEST AND DUMMY VARIABLE GROUP TEST В тесте Чоу мы тоже начинаем с оценки параметров регрессии по всем наблюдениям. 14
CHOW TEST AND DUMMY VARIABLE GROUP TEST В тесте Чоу мы тоже начинаем с оценки параметров регрессии по всем наблюдениям. 14
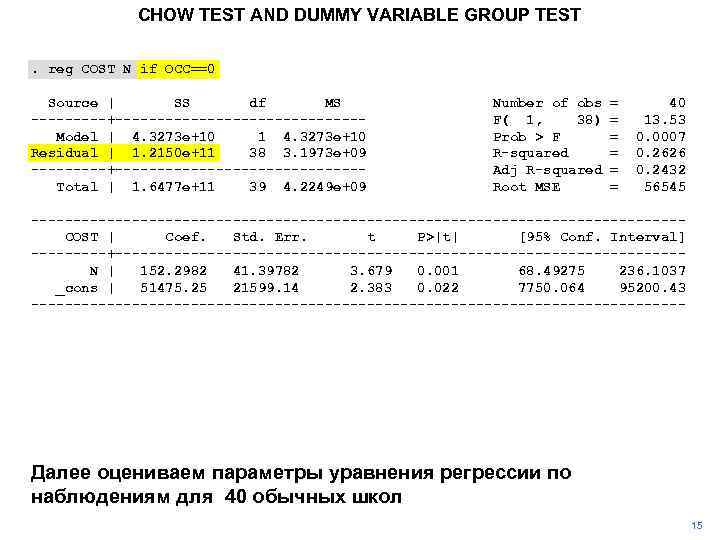 CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N if OCC==0 Source | SS df MS -----+---------------Model | 4. 3273 e+10 1 4. 3273 e+10 Residual | 1. 2150 e+11 38 3. 1973 e+09 -----+---------------Total | 1. 6477 e+11 39 4. 2249 e+09 Number of obs F( 1, 38) Prob > F R-squared Adj R-squared Root MSE = = = 40 13. 53 0. 0007 0. 2626 0. 2432 56545 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 41. 39782 3. 679 0. 001 68. 49275 236. 1037 _cons | 51475. 25 21599. 14 2. 383 0. 022 7750. 064 95200. 43 --------------------------------------- Далее оцениваем параметры уравнения регрессии по наблюдениям для 40 обычных школ 15
CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N if OCC==0 Source | SS df MS -----+---------------Model | 4. 3273 e+10 1 4. 3273 e+10 Residual | 1. 2150 e+11 38 3. 1973 e+09 -----+---------------Total | 1. 6477 e+11 39 4. 2249 e+09 Number of obs F( 1, 38) Prob > F R-squared Adj R-squared Root MSE = = = 40 13. 53 0. 0007 0. 2626 0. 2432 56545 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 152. 2982 41. 39782 3. 679 0. 001 68. 49275 236. 1037 _cons | 51475. 25 21599. 14 2. 383 0. 022 7750. 064 95200. 43 --------------------------------------- Далее оцениваем параметры уравнения регрессии по наблюдениям для 40 обычных школ 15
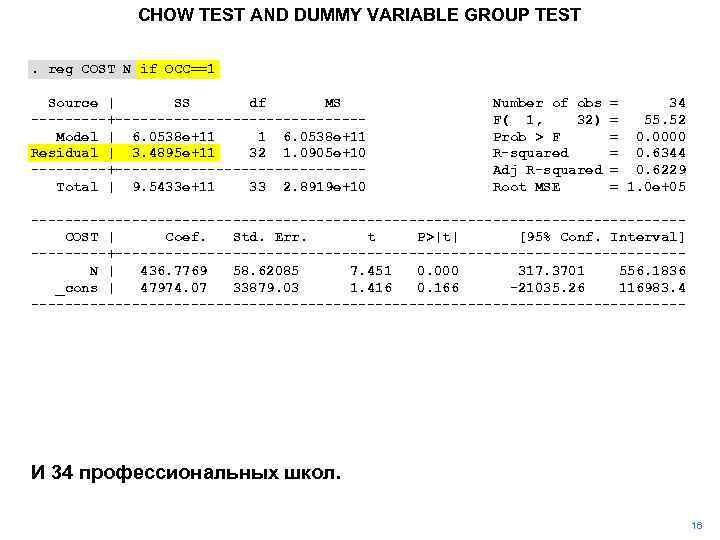 CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N if OCC==1 Source | SS df MS -----+---------------Model | 6. 0538 e+11 1 6. 0538 e+11 Residual | 3. 4895 e+11 32 1. 0905 e+10 -----+---------------Total | 9. 5433 e+11 33 2. 8919 e+10 Number of obs F( 1, 32) Prob > F R-squared Adj R-squared Root MSE = 34 = 55. 52 = 0. 0000 = 0. 6344 = 0. 6229 = 1. 0 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 436. 7769 58. 62085 7. 451 0. 000 317. 3701 556. 1836 _cons | 47974. 07 33879. 03 1. 416 0. 166 -21035. 26 116983. 4 --------------------------------------- И 34 профессиональных школ. 16
CHOW TEST AND DUMMY VARIABLE GROUP TEST. reg COST N if OCC==1 Source | SS df MS -----+---------------Model | 6. 0538 e+11 1 6. 0538 e+11 Residual | 3. 4895 e+11 32 1. 0905 e+10 -----+---------------Total | 9. 5433 e+11 33 2. 8919 e+10 Number of obs F( 1, 32) Prob > F R-squared Adj R-squared Root MSE = 34 = 55. 52 = 0. 0000 = 0. 6344 = 0. 6229 = 1. 0 e+05 ---------------------------------------COST | Coef. Std. Err. t P>|t| [95% Conf. Interval] -----+----------------------------------N | 436. 7769 58. 62085 7. 451 0. 000 317. 3701 556. 1836 _cons | 47974. 07 33879. 03 1. 416 0. 166 -21035. 26 116983. 4 --------------------------------------- И 34 профессиональных школ. 16
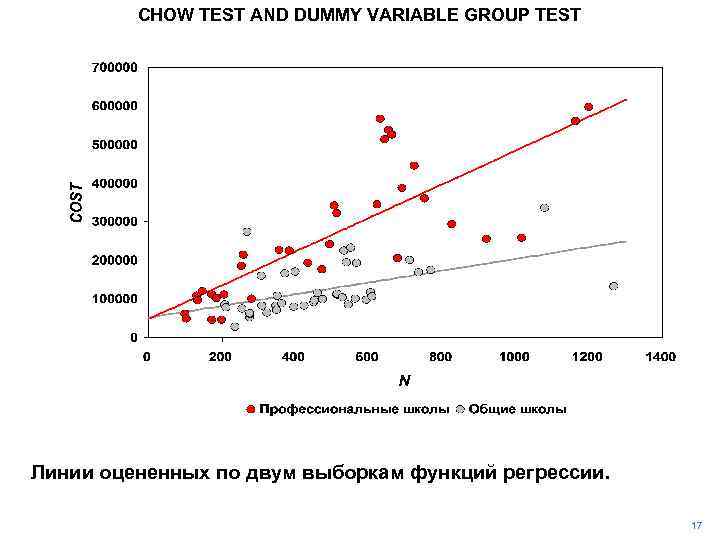 CHOW TEST AND DUMMY VARIABLE GROUP TEST Линии оцененных по двум выборкам функций регрессии. 17
CHOW TEST AND DUMMY VARIABLE GROUP TEST Линии оцененных по двум выборкам функций регрессии. 17
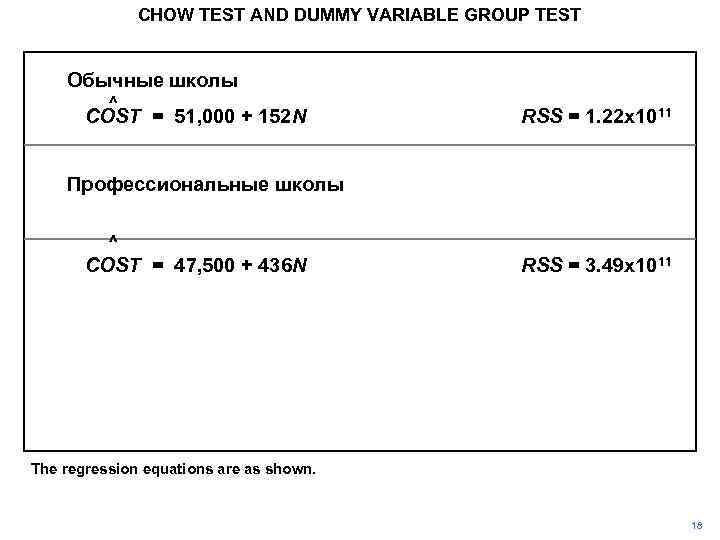 CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 500 + 436 N RSS = 3. 49 x 1011 The regression equations are as shown. 18
CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 500 + 436 N RSS = 3. 49 x 1011 The regression equations are as shown. 18
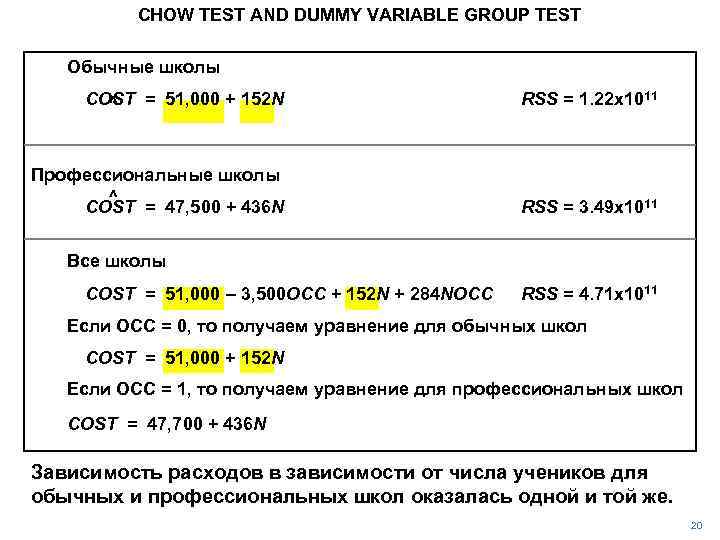 CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы COST = 51, 000 + 152 N ^ RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 500 + 436 N RSS = 3. 49 x 1011 Все школы COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 Если OCC = 0, то получаем уравнение для обычных школ COST = 51, 000 + 152 N Если OCC = 1, то получаем уравнение для профессиональных школ COST = 47, 700 + 436 N Зависимость расходов в зависимости от числа учеников для обычных и профессиональных школ оказалась одной и той же. 20
CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы COST = 51, 000 + 152 N ^ RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 500 + 436 N RSS = 3. 49 x 1011 Все школы COST = 51, 000 – 3, 500 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 Если OCC = 0, то получаем уравнение для обычных школ COST = 51, 000 + 152 N Если OCC = 1, то получаем уравнение для профессиональных школ COST = 47, 700 + 436 N Зависимость расходов в зависимости от числа учеников для обычных и профессиональных школ оказалась одной и той же. 20
 CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 000 + 436 N RSS = 3. 49 x 1011 Все школы ^ COST = 51, 000 - 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 F – статистики в тесте о значимости группы dummy – переменных и тесте Chow совпадают. 25
CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 000 + 436 N RSS = 3. 49 x 1011 Все школы ^ COST = 51, 000 - 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 F – статистики в тесте о значимости группы dummy – переменных и тесте Chow совпадают. 25
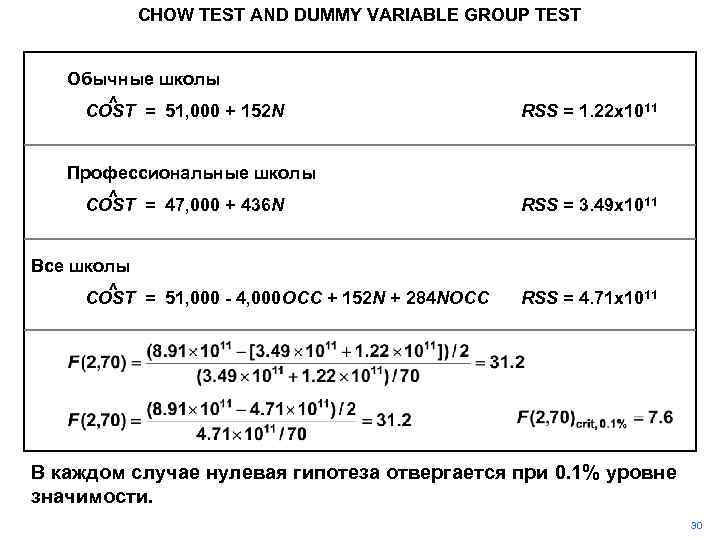 CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 000 + 436 N RSS = 3. 49 x 1011 Все школы ^ COST = 51, 000 - 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 В каждом случае нулевая гипотеза отвергается при 0. 1% уровне значимости. 30
CHOW TEST AND DUMMY VARIABLE GROUP TEST Обычные школы ^ COST = 51, 000 + 152 N RSS = 1. 22 x 1011 Профессиональные школы ^ COST = 47, 000 + 436 N RSS = 3. 49 x 1011 Все школы ^ COST = 51, 000 - 4, 000 OCC + 152 N + 284 NOCC RSS = 4. 71 x 1011 В каждом случае нулевая гипотеза отвергается при 0. 1% уровне значимости. 30


