Лекция 11 Движения первого и второго родов Аналитическое

Лекция 11 Движения первого и второго родов. Аналитическое выражение движения. Леммы о инвариантных точках и прямых движения. Литература. [1] §§ 42, 43.

Два репера и одинаково ориентированы, если определитель матрицы перехода от одного репера ко второму положителен. Ориентации различны, если он меньше нуля. • Теорема 1. Пусть d - движение плоскости, и - реперы, - их образы при этом движении. Тогда ориентации реперов и совпадают в том и только в том случае, когда совпадают ориентации реперов и. •

Определение Движение g плоскости называется движением первого рода, если ориентация любого репера R совпадает с ориентацией его образа R' = g(R ). Это движение называется движением второго рода, если ориентация любого репера R противоположна ориентации его образа R'.

Параллельный перенос и вращение представляют собой движение первого рода. Осевая симметрия является движением второго рода.

Теорема Движения первого рода образуют подгруппу в группе движений плоскости. Произведение двух движений второго рода является движением первого рода.

Аналитическое выражение движения Здесь род, и = 1, если движение имеет первый = -1, если оно второго рода

Определение Фигура P называется инвариантной относительно преобразования f, если её образ совпадает с P: f(P)=P. Лемма 1. Если движение имеет три инвариантные точки, не лежащие на одной прямой, то оно совпадает с тождественным преобразованием. Лемма 2. Если движение g имеет две неподвижные точки O 1 и O 2, то каждая точка прямой O 1 O 2 является инвариантной. Лемма 3. Если при движении g образы точек P и Q принадлежат прямой PQ, то эта прямая инвариантна

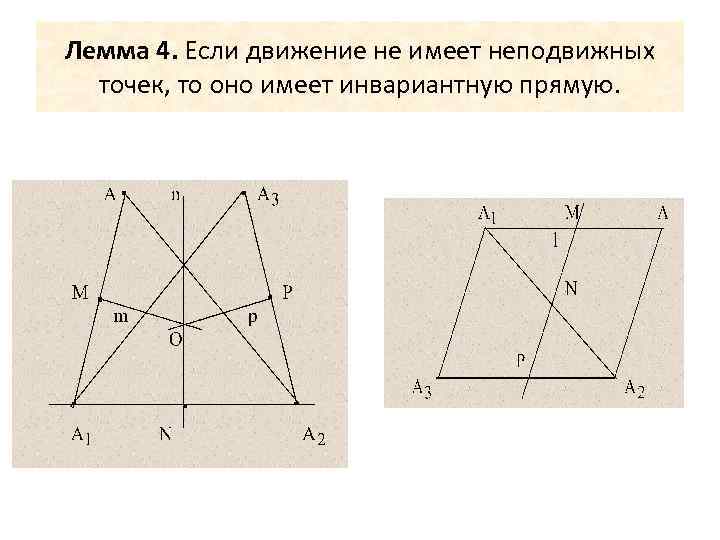Лемма 4. Если движение не имеет неподвижных точек, то оно имеет инвариантную прямую.