Лекция 11 12 ДЕРЕВЬЯ ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ План

Лекция 11, 12 ДЕРЕВЬЯ, ПРЕОБРАЗОВАНИЕ ВЫРАЖЕНИЙ

План лекции Дерево, поддерево и др. определения Обходы деревьев Представление деревьев Дерево двоичного поиска АВЛ деревья

Дерево (Ориентированным) деревом Т называется (ориентированный) граф G = (А, R) со специальной вершиной r А, называемой корнем, у которого степень по входу вершины r равна 0, степень по входу всех остальных вершин равна 1, каждая вершина а А достижима из r. Базовые свойства деревьев Дерево не содержит циклов Каждая вершина дерева соединяется с его корнем единственным путём

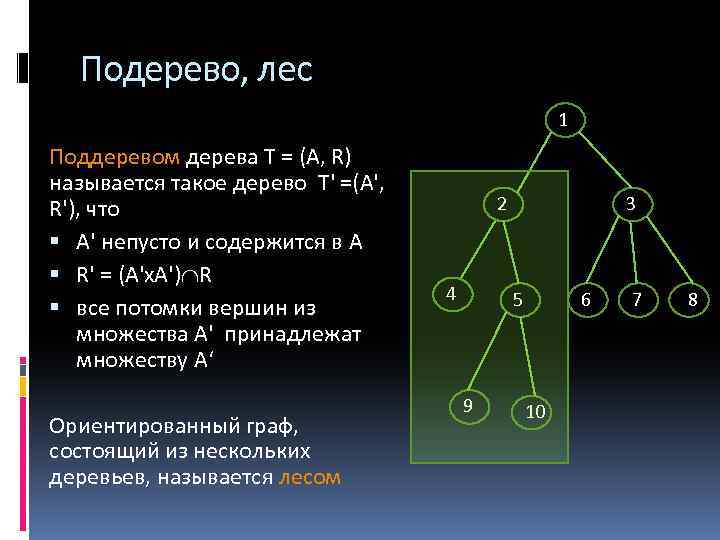
Подерево, лес 1 Поддеревом дерева Т = (А, R) называется такое дерево T' =(А', R'), что А' непусто и содержится в A R' = (A'х. A') R все потомки вершин из множества А' принадлежат множеству А‘ Ориентированный граф, состоящий из нескольких деревьев, называется лесом 2 4 3 5 9 6 10 7 8

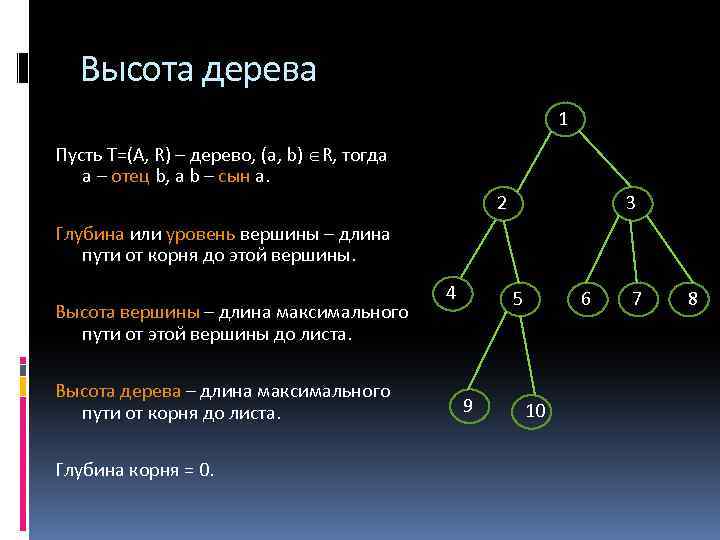
Высота дерева 1 Пусть Т=(A, R) – дерево, (a, b) R, тогда a – отец b, а b – сын a. 2 3 Глубина или уровень вершины – длина пути от корня до этой вершины. Высота вершины – длина максимального пути от этой вершины до листа. Высота дерева – длина максимального пути от корня до листа. Глубина корня = 0. 4 5 9 6 10 7 8

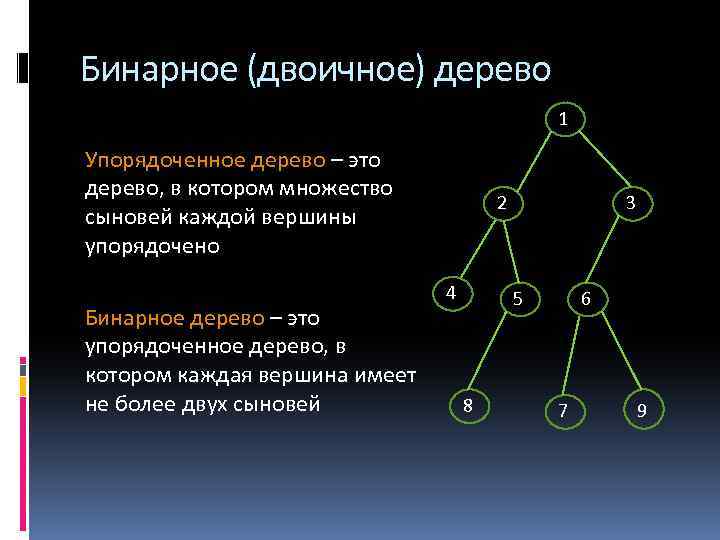
Бинарное (двоичное) дерево 1 Упорядоченное дерево – это дерево, в котором множество сыновей каждой вершины упорядочено Бинарное дерево – это упорядоченное дерево, в котором каждая вершина имеет не более двух сыновей 2 4 3 5 8 6 7 9

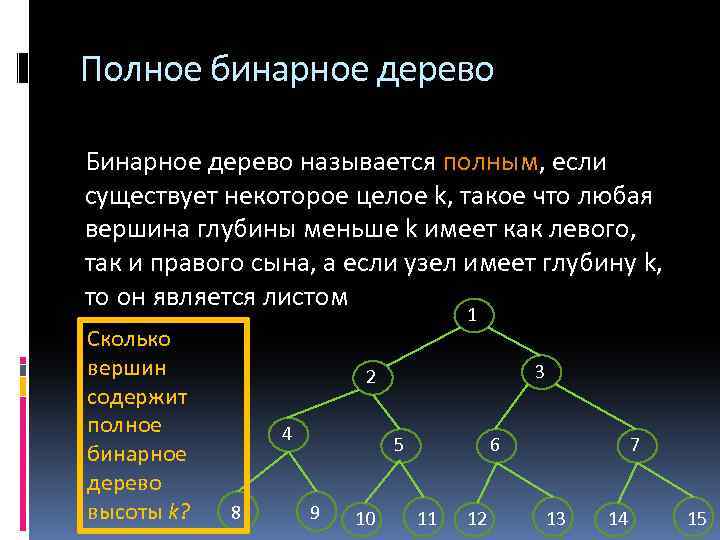
Полное бинарное дерево Бинарное дерево называется полным, если существует некоторое целое k, такое что любая вершина глубины меньше k имеет как левого, так и правого сына, а если узел имеет глубину k, то он является листом Сколько вершин содержит полное бинарное дерево высоты k? 1 3 2 4 8 5 9 10 6 11 12 7 13 14 15

Обходы деревьев Обход дерева – это способ перечисления (нумерации) вершин дерева, при котором каждая вершина получает единственный номер в глубину Обходы в ширину

Обходы в глубину Пусть T – дерево, r - корень, v 1, v 2, …, vn – сыновья вершины r. Прямой (префиксный) обход: посетить (пронумеровать) корень r; посетить в прямом порядке поддеревья с корнями v 1, v 2, …, vn. Обратный (постфиксный) обход: посетить в обратном порядке поддеревья с корнями v 1, v 2, …, vn; посетить корень r. Внутренний ( инфиксный) обход для бинарных деревьев: посетить во внутреннем порядке левое поддерево корня r (если существует); посетить корень r; посетить во внутреннем порядке правое поддерево корня r (если существует).

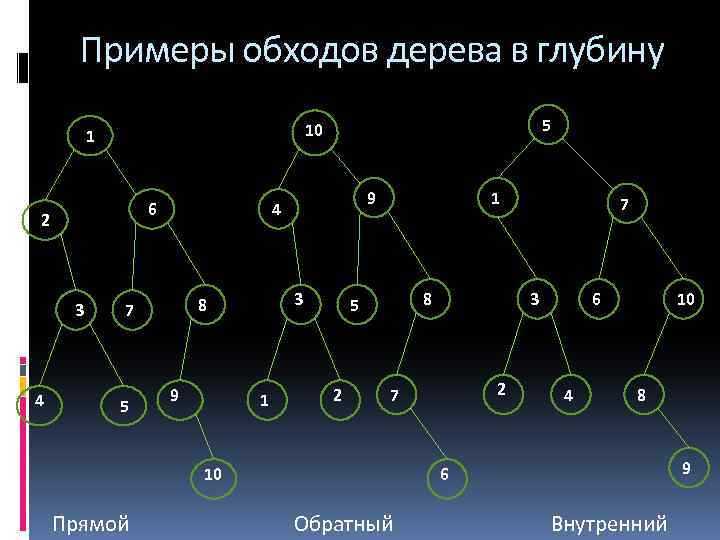
Примеры обходов дерева в глубину 6 2 3 4 5 10 1 3 8 7 5 9 4 9 1 1 8 5 2 Прямой 3 2 7 10 7 6 4 10 8 9 6 Обратный Внутренний

Обход деревьев в ширину Обход вершин дерева по уровням от корня слева направо (или справа налево) Алгоритм обхода дерева в ширину Шаг 0: Поместить в очередь корень дерева Шаг 1: Взять из очереди очередную вершину Поместить в очередь всех ее сыновей по порядку слева направо (справа налево) Шаг 2: Если очередь пуста, то конец обхода, иначе перейти на Шаг 1 Какой обход получится, если заменить очередь на стек?

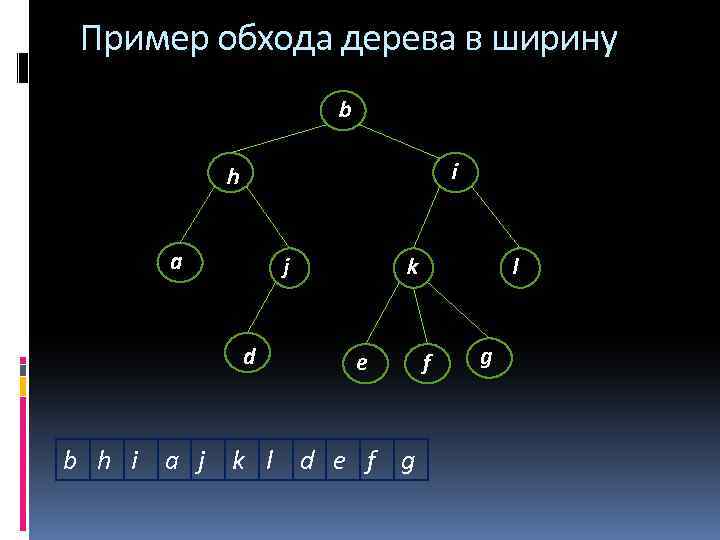
Пример обхода дерева в ширину b i h a j d k e b h i a j k l d e f g l f g

Бинарное дерево -- операции T Tree ptr. Element -- тип данных -- двоичное дерево с данными типа Т -- указатель на вершины дерева void insert(Tree *t, T value); void erase(Tree *t, T value); int find(Tree *t, T value);

Представление бинарных деревьев с помощью указателей struсt Element { T data; // данные struct Element *left; // левое п/дерево struct Element *right; // правое п/дерево }; struct Tree { struct Element *root; }; typedef struct Tree; typedef Element * ptr. Element;

0 2*i+1 2*i+2 0 (i-1) div 2

Пример представления с помощью массива A[0] A[1] A[3] A[7] A[8] A[2] A[4] A[5] A[6] A[9] A[10] A[11] A[12] A[13] A[14]

Скобочное представление деревьев Левое и правое скобочные представления Lrep(Т) и Rrep(Т) дерева Т строятся по следующим рекурсивным правилам 1. Если корнем дерева Т служит вершина а, не имеющая прямых потомков, то Lrep (Т) = Rrep(T) = а 2. Если корнем дерева Т служит вершина а с поддеревьями T 1, Т 2, . . . , Тn, расположенными в этом порядке (их корни — прямые потомки вершины а), то Lrep(Т) = а(Lrep (T 1), Lrep (Т 2) , . . . , Lrep (Тn)) Rrep(Т) = (Rrep(Т 1), Rrep(T 2), . . . , Rrep (Тn))а

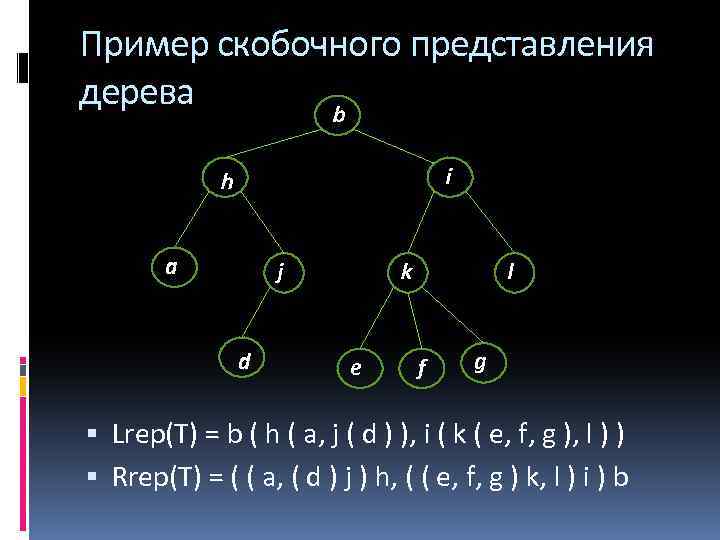
Пример скобочного представления дерева b i h a j d k e l f g Lrep(T) = b ( h ( a, j ( d ) ), i ( k ( e, f, g ), l ) ) Rrep(T) = ( ( a, ( d ) j ) h, ( ( e, f, g ) k, l ) i ) b

$Пример печати левого скобочного представления двоичного дерева void print_Lrep(Tree t) { print_Lrep_body(t. root); }$

Пример печати левого скобочного представления двоичного дерева void print_Lrep(Tree t) { print_Lrep_body(t. root); } void print_Lrep_body(ptr. Element t) { if (t == NULL) return; printf("%d(", t->data); // считаем T = int print_Lrep(t->left); print_Lrep(t->right); printf(")"); }

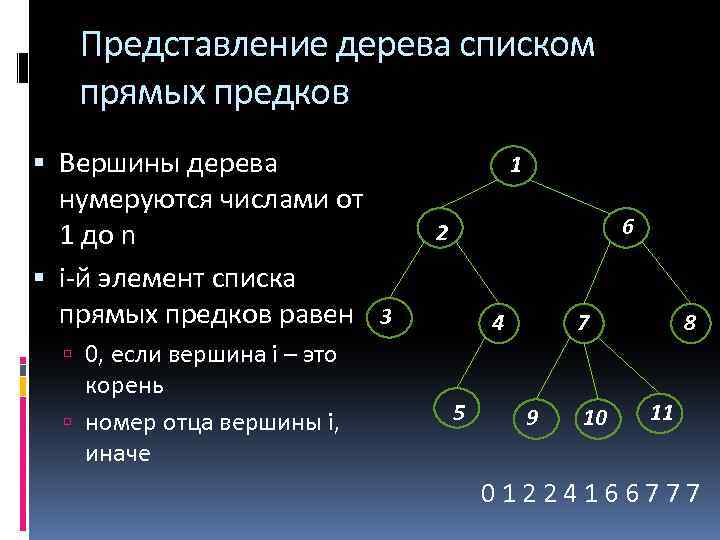
Представление дерева списком прямых предков Вершины дерева нумеруются числами от 1 до n i-й элемент списка прямых предков равен 3 1 6 2 4 7 8 0, если вершина i – это корень номер отца вершины i, иначе 5 9 10 11 01224166777

Дерево двоичного поиска Деревом двоичного поиска для множества S называется помеченное двоичное дерево, каждый узел v которого помечен элементом l(v) S так, что 1. l(u) < l(v) для каждого узла u из левого поддерева узла v, 2. l(w) > l(v) для каждого узла w из правого поддерева узла v, 3. для любого элемента a S существует единственный узел v , такой что l(v) = a.

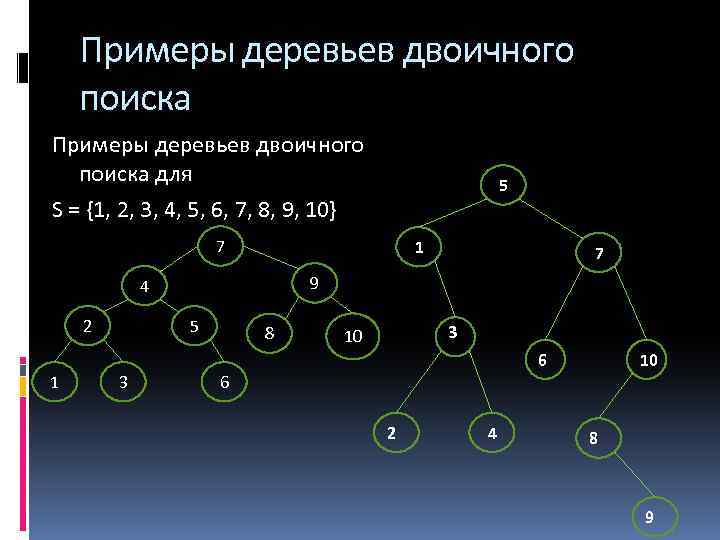
Примеры деревьев двоичного поиска для S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} 5 7 1 9 4 2 7 5 8 3 10 6 1 3 10 6 2 4 8 9

Поиск в дереве двоичного поиска Вход Дерево Д двоичного поиска для множества S, элемент a. Выход истина, если a S ложь иначе логическая функция ПОИСК (a, Lrep(Д)) { если Lrep(Д) == x, то вернуть I(x) == a; иначе Lrep(Д) = x(Л, П); если а == I(х), то вернуть истина; иначе если a < I(x), то вернуть ПОИСК(а, Л); иначе вернуть ПОИСК(а, П); всё; Как обойтись всё; } без рекурсии?

Сбалансированные деревья АВЛ Время вставки вершины в дерево двоичного поиска, содержащее n вершин O(log 2 n) в лучшем случае для полных деревьев O(n) в худшем случае для вырожденных деревьев, имеющих структуру списка Можно устранить вырождение дерева в список и сократить время вставки вершины с O(n) до O(log 2 n) даже в худшем случае Г. М. Адельсон-Вельский, Е. М. Ландис. Один алгоритм организации информации // Доклады АН СССР. 1962. Т. 146, № 2. C. 263– 266 Дерево двоичного поиска сбалансировано, если высоты поддеревьев каждой из его вершин отличаются не более, чем на единицу

Вставка вершины в АВЛ дерево авл_вставка(значение x, дерево двоичного поиска T) если Т == NULL, то вернуть x(NULL, NULL) иначе T имеет вид a(L, R); TТ = x < a ? a(авл_вставка(L), R) : a(L, авл_вставка(R)); Восстановить сбалансированность в корне дерева ТТ и вернуть получившееся дерево всё

Вставка узла в АВЛ дерево Если высота ТТ == высота T, то сбалансированность сохранилась Если высота ТТ == высота T + 1 и х < a, то возможны три случая – считаем, что T имеет вид a(L, R) h. L == h. R сбалансированность сохранилась 2. h. L < h. R сбалансированность сохранилась 3. h. L > h. R сбалансированность нарушилась 1. Что делать, если высота ТТ == высота T + 1 и х > a? h. L 1 a h. R L R

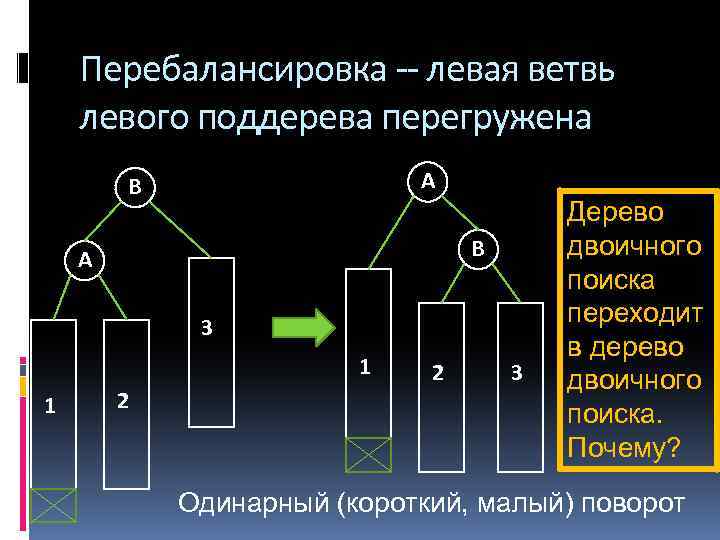
Перебалансировка -- левая ветвь левого поддерева перегружена A B B A 3 1 1 2 2 3 Дерево двоичного поиска переходит в дерево двоичного поиска. Почему? Одинарный (короткий, малый) поворот

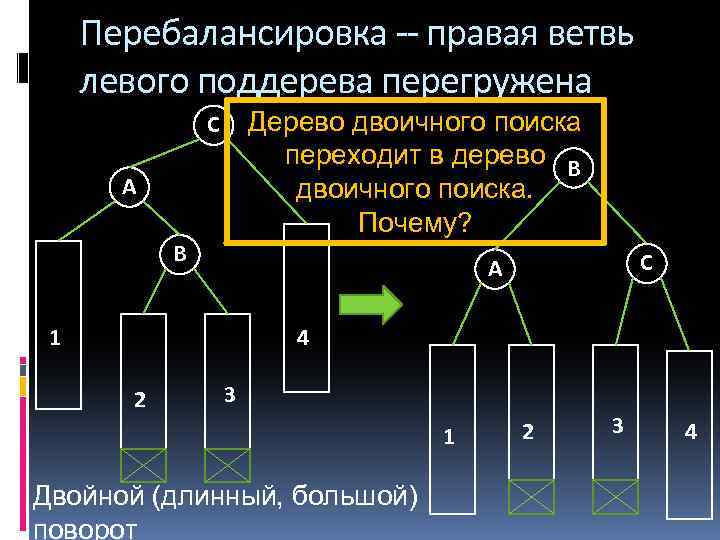
Перебалансировка -- правая ветвь левого поддерева перегружена Дерево двоичного поиска переходит в дерево B двоичного поиска. Почему? С A B С A 1 4 2 3 1 Двойной (длинный, большой) поворот 2 3 4

Оптимизация работы с АВЛ-деревьями -показатель сбалансированности Операции вставки и удаления узла отслеживают разность высот левого и правого поддеревьев balance. Factor(x(L, R)) = height(L) - height(R) В АВЛ-дереве показатель сбалансированности должен быть -1, 0, или 1 -1: Высота левого поддерева на 1 больше высоты правого поддерева 0: Высоты поддеревьев одинаковы +1: Высота правого поддерева на 1 больше высоты левого поддерева

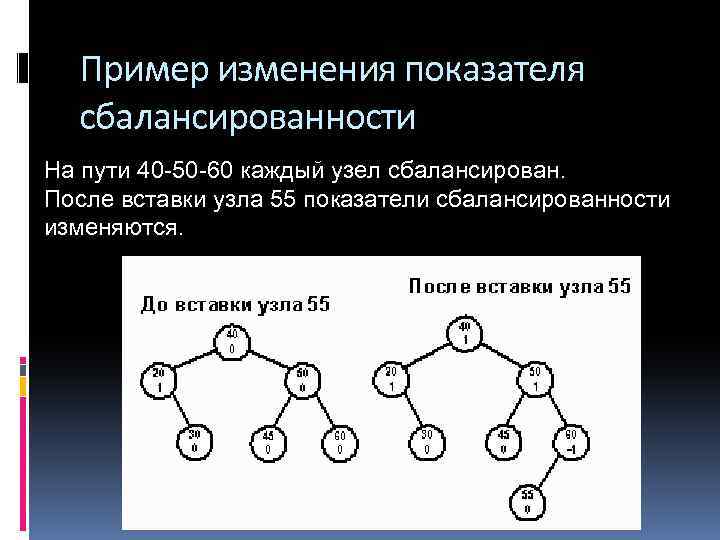
Пример изменения показателя сбалансированности На пути 40 -50 -60 каждый узел сбалансирован. После вставки узла 55 показатели сбалансированности изменяются.

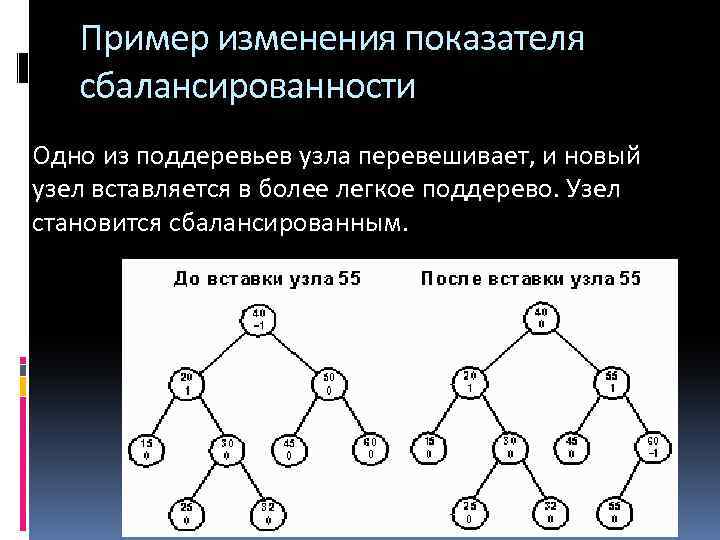
Пример изменения показателя сбалансированности Одно из поддеревьев узла перевешивает, и новый узел вставляется в более легкое поддерево. Узел становится сбалансированным.

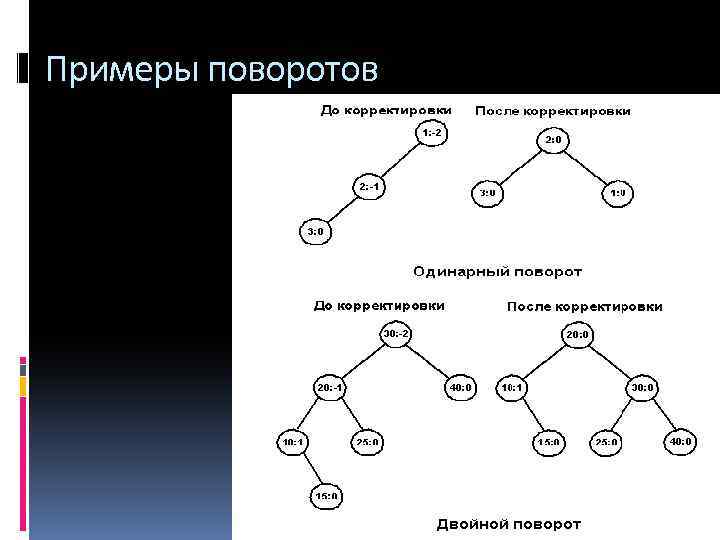
Примеры поворотов

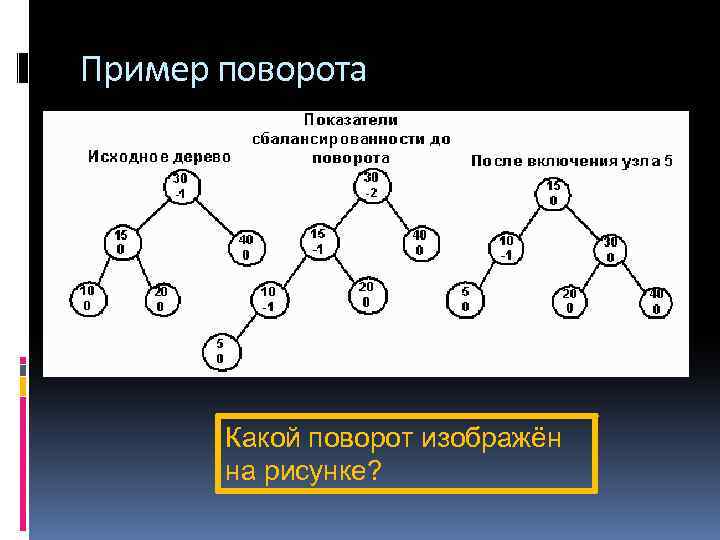
Пример поворота Какой поворот изображён на рисунке?

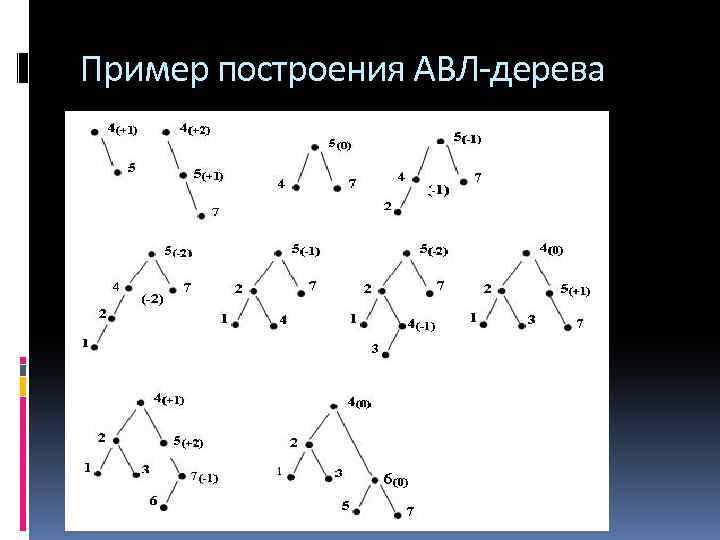
Пример построения АВЛ-дерева

Заключение Дерево, поддерево и др. определения Основные свойства Обходы деревьев В ширину, в глубину Представление деревьев Указатели, массив, скобочная запись, список прямых предков Дерево двоичного поиска АВЛ деревья

Материал второго семестра

Красно-чёрное дерево (Red-Black. Tree, RB-Tree) Красно-чёрное дерево – это дерево двоичного поиска, обладающее следующими свойствами 1. Все листья чёрные 2. Все потомки красных узлов чёрные – нет двух красных узлов подряд 3. На всех путях от корня к листьям число чёрных узлов одинаково Это число называется чёрной высотой дерева Для удобства листьями красно-чёрного дерева считаются NULL-узлы, не содержащие данных Красно-чёрные ДДП 1978 Л. Гимпас и Р. Седжвик

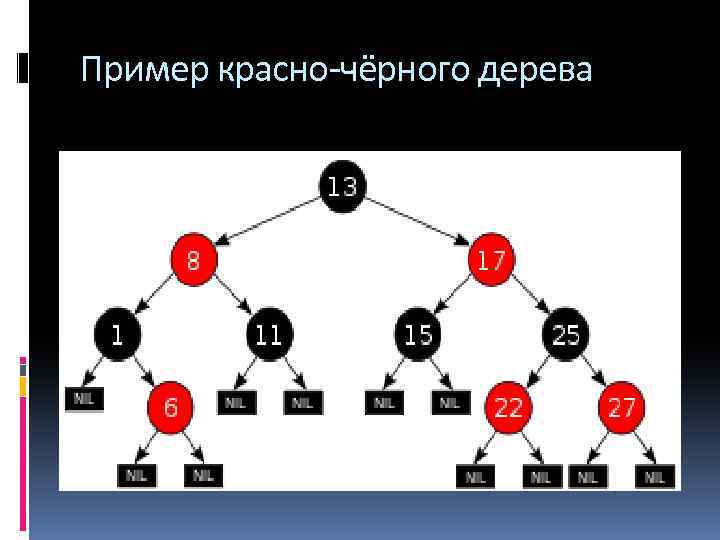
Пример красно-чёрного дерева

Связь между высотой и числом узлов в красно-чёрных деревьях 1. Если h - чёрная высота дерева, то количество узлов не менее 2 h − 1 2. Если h - высота дерева, то количество узлов не менее 2(h− 1)/2 3. Если количество узлов N, высота дерева не больше 2 log 2 N + 1

Сравнение с высотой АВЛ-дерева Обозначим N(h) = минимальное число узлов в дереве высоты h N(h) для АВЛ-дерева N(h) = N(h − 1) + N(h − 2) + 1, N(0) = 1, N(1) = 2 N(h) растёт как последовательность Фибоначчи Следовательно, N(h) = Θ(λh), где N(h) для красно-чёрного дерева Свойство 3 красно-чёрных деревьев ==> При том же количестве узлов красно-чёрное дерево может быть выше АВЛ-дерева, но не более чем раз.

Вставка узла в красно-чёрное дерево Чтобы вставить узел, мы сначала Находим двоичным поиском в дереве место, куда его следует добавить Новый узел добавляем как красный лист с двумя чёрными NULL-потомками После этого восстанавливаем красно-чёрные свойства -перекрашиваем узлы и поворачиваем поддеревья если необходимо Вставка красного узла с двумя черными NULL-потомками 1. Все листья чёрные – сохраняется 2. Все потомки красных узлов чёрные – нет двух красных узлов подряд – может нарушиться 3. На всех путях от корня к листьям число чёрных узлов одинаково – сохраняется

Вставка нового узла Случай 1 Если отец и дядя (другой сын деда вставляемого узла) оба красные, тогда цвет отца и дяди меняется на черный, а цвет деда на красный Нарушение красно-чёрного свойства перемещается на 2 уровня вверх, и операция повторяется уже для деда узла Обратите внимание на распространение влияния красного узла на верхние узлы дерева. В самом конце корень мы красим в черный цвет корень дерева. Если он был красным, то при этом увеличивается черная высота дерева. Случай 2 Если отец нового узла красный, а дядя черный, то возможны два похожих подслучая. Случай 2 а Если новый узел левый сын своего отца, тогда цвет отца меняется на черный, цвет деда меняется на красный и дерево поворачивается направо вокруг отца нового узла. Таким образом нарушение полностью устраняется и алгоритм завершается. Случай 2 б Если новый узел правый сын своего отца, то сначала осуществляется левый поворот вокруг отца и затем выполняется все как в случае 2.

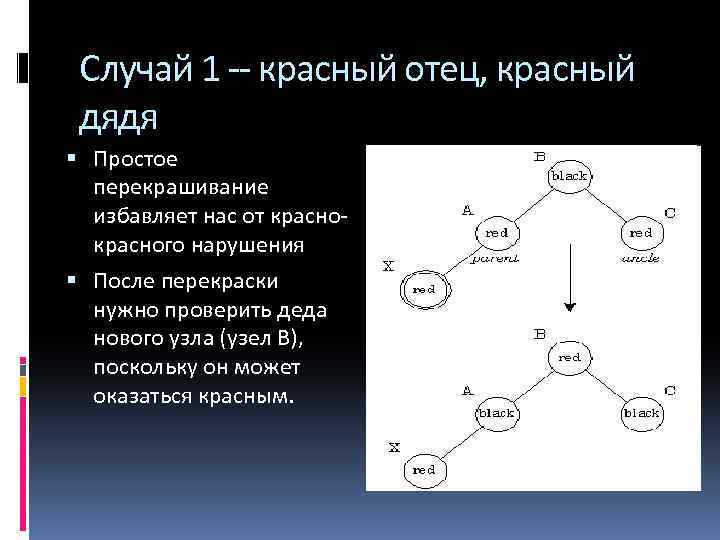
Случай 1 -- красный отец, красный дядя Простое перекрашивание избавляет нас от красного нарушения После перекраски нужно проверить деда нового узла (узел B), поскольку он может оказаться красным.

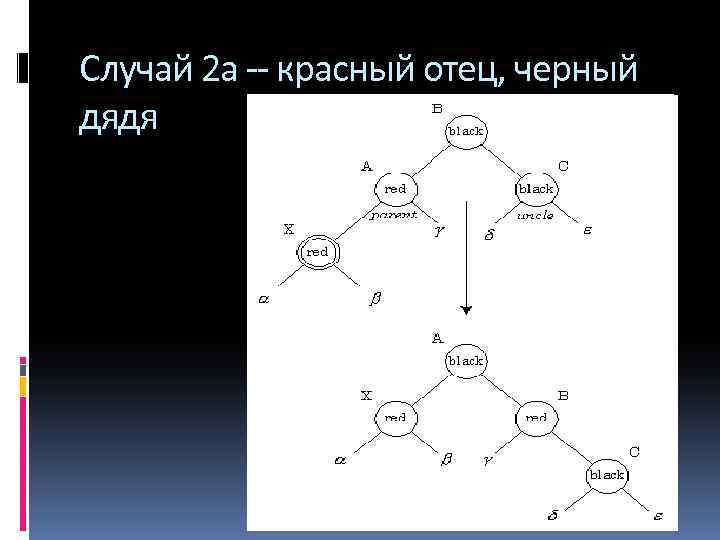
Случай 2 а -- красный отец, черный дядя

Сравнение с АВЛ-деревом -- поиск, вставка, удаление вершины Поиск и вставка в красно-чёрном дереве медленнее, чем в АВЛ- дереве, из-за большей высоты Проигрыш по времени не превышает 40% Удаление – не рассматриваем на лекциях Удаление из красно-чёрного дерева может быть быстрее, чем из АВЛ-дерева Удаление узла из красно-чёрного дерева требует до 3 поворотов Удаление узла из АВЛ-дерева в худшем случае требует поворота в каждом узле на пути от удаляемого листа до корня Память Объём дополнительной памяти практически одинаковый 2 бита на узел в АВЛ-дереве 1 бит на узел в красно-чёрном дереве

Использование в библиотеке стандартных шаблонов С++ (STL) Класс АВЛ-деревьев исторически был первым примером использования сбалансированных деревьев В настоящее время более популярен класс красно -чёрных деревьев Красно-чёрные и АВЛ-деревья используются в стандартной библиотеке шаблонов языка C++ STL для реализации множества и ассоциативного массива (классы set и map) В какой стране родился автор STL?

КОНЕЦ ЛЕКЦИИ

Удаление узла Если удаляемый узел красный все правила сохраняются и все прекрасно. Если же удаляемый узел черный, требуется значительное количество кода, для поддержания дерева частично сбалансированным. Как и в случае вставки в красно-черное дерево, здесь также существует несколько различных случаев.

Связь с B-деревьями RB- дерево можно рассматривать как двоичное дерево, построенное из B-дерева с максимальным количеством потомков у любой вершины = 4, по следующим правилам: 1) Каждый узел окрашен либо в красный, либо в чёрный цвет. 2) Вершина с количеством потомков ≤ 2 переносится в бинарное дерево без изменений и окрашивается в чёрный цвет. 3) В вершине с количеством потомков = 3 первый потомок присоединяется непосредственно, а другие два - через соединительный узел, соединительные узлы окрашиваются в красный цвет, остальные остаются чёрными. 4) К вершине с количеством потомков = 4 потомки присоединяются через два Соединительных узла красного цвета (по два к каждому). Таким образом получаем бинарное дерево, являющееся моделью B-дерева с максимальным количеством потомков у вершины = 4. В исходном B-дереве (так как оно сбалансировано) все пути от корня до любого листа имеют одинаковую длину. По построению очевидно, что любой путь в RBдереве возрастает не более чем в два раза. Таким образом, можем получить минимальный путь, равным по длине пути в исходном дереве, и максимальный, превышающий по длине путь в исходном дереве в два раза.

Утверждение n – количество концевых вершин m – неотрицательное целое d – длина пути от корня до вершины Дерево сблалансировано, если 1) n = 2 m d = m 2) 2 m < n < 2 m d = m + 1 2) 1) ( 1 2)

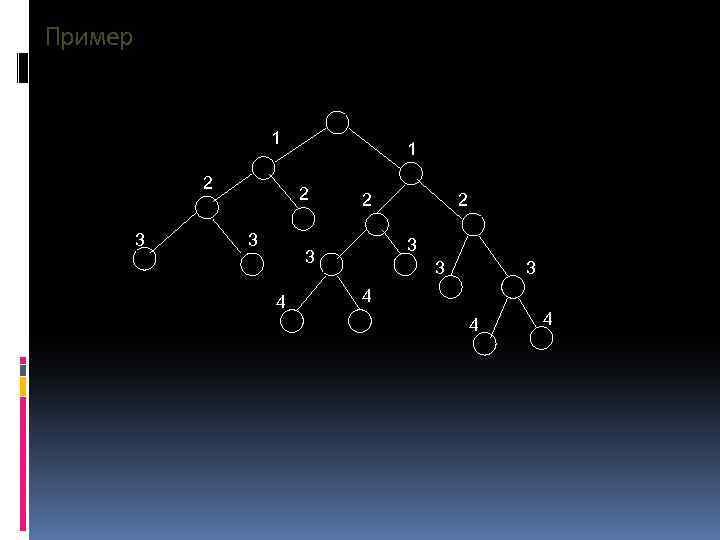
Пример 1 2 3 2 3 3 4 4 4

Три возможных ситуации Случай 1 Узел на поисковом маршруте изначально является сбалансированным (balance. Factor = 0). После вставки в поддерево нового элемента узел стал перевешивать влево или вправо в зависимости от того, в какое поддерево была произведена вставка. Если элемент вставлен в левое поддерево, показателю сбалансированности присваивается -1, а если в правое, то 1.

Случай 3 Одно из поддеревьев узла перевешивает, и новый узел помещается в более тяжелое поддерево. Тем самым нарушается условие сбалансированности, так как balance. Factor выходит за пределы -1. . 1. Чтобы восстановить равновесие, нужно выполнить поворот.

Правая ветвь левого поддерева перегружена

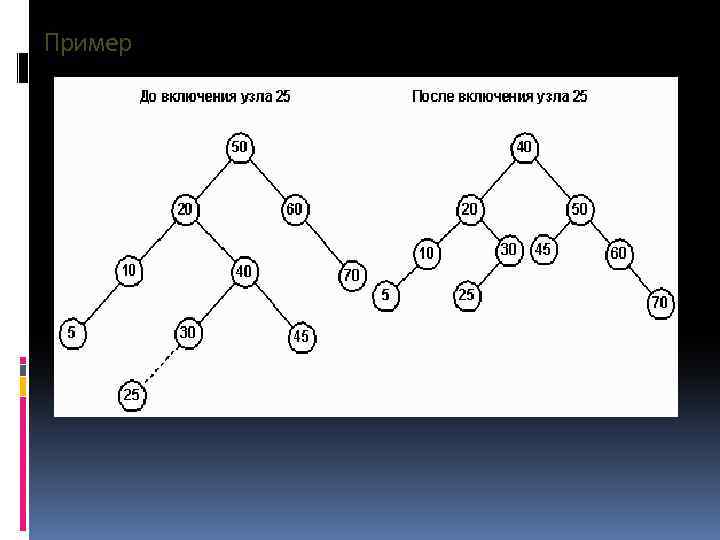
Пример