Лекция 1 ВВЕДЕНИЕ ПОНЯТИЕ МОДЕЛИ И МАТЕМАТИЧЕСКОГО

Лекция № 1 «ВВЕДЕНИЕ. ПОНЯТИЕ МОДЕЛИ И МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ» 1 Лектор к. г. -м. н. , доцент каф. ГИГЭ ИПР Токаренко Ольга Григорьевна Лекции – 8 ч (4 лекции) Практические занятия – 24 ч (12 занятий) Вид промежуточной аттестации – ЗАЧЕТ 2012/2013 учебный год Дисциплина "Математическое моделирование процессов в компонентах природы"

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ПО ДИСЦИПЛИНЕ 2 Основная 1. 2. 3. 4. 5. Кузеванов К. И. , Савичев О. Г. , Решетько М. В. Математическое моделирование процессов в компонентах природы: учебное пособие. — Томск: Изд-во ТПУ, 2011. — 146 с. Методы геохимического моделирования и прогнозирования в гидрогеологии / Под ред. Крайнова С. Р. - М. : Недра, 1988. - 254 с. Поротов Г. С. Математические методы моделирования в геологии: Учебник / Санкт-Петербургский государственный горный институт (технический университет). СПб, 2006. 223 с. Геологическая эволюция и самоорганизация системы вода-порода. Т. 1 Система вода-порода в земной коре: взаимодействие, кинетика, равновесие, моделирование // Под ред. С. Л. Шварцева. Новосибирск: Изд. СО РАН, 2005. - 244 с. Букаты М. Б. Геоинформационные системы и математическое моделирование. Учеб. пособие. - Томск: изд. ТПУ, 2002. - 75 с. Дисциплина "Математическое моделирование процессов в компонентах природы"

Дополнительная 1. 2. 3. 4. 5. Крайнов С. Р. , Рыженко Б. Н. , Швец В. М. Геохимия подземных вод. Теоретические, прикладные и экологические аспекты. - М. : Наука, 2004. - 677 с. Термодинамическое моделирование в геологии: минералы, флюиды и расплавы/ Р. К. Ньютон, А. Навротеки, Б. Дж. Вуд и др. М. : Мир, 1992. - 534 с. Langmuir D. Aqueous Environmental Geochemistry. - London: Prentice. Hall International, 1997. - 601 pp. Мироненко B. A. , Румынин В. Г. Проблемы гидрогеоэкологии. Т. 1 Теоретическое изучение и моделирование геомиграционных процессов. - М. : Изд-во МГУ, 1998. - 611 с. Гидрогеодинамические расчеты на ЭВМ. Учебное пособие / Под ред. Штенгелова PC. - М. : Изд-во МГУ, 1994. - 335 с. Дисциплина "Математическое моделирование процессов в компонентах природы" 3

ПЛАН ЛЕКЦИИ 4 1. Положение дисциплины среди дисциплин геологического профиля 2. Определение направления и объектов при изучении дисциплины 3. Понятие модели и моделирования 4. Типы геолого-математических моделей 5. Моделирование как метод исследования 6. Классификация моделей 7. Этапы построения математической модели 8. Концептуальная и математическая постановка задачи моделирования Дисциплина "Математическое моделирование процессов в компонентах природы"

5 ПОЛОЖЕНИЕ ДИСЦИПЛИНЫ В СИСТЕМЕ ДИСЦИПЛИН ГЕОЛОГИЧЕСКОГО ПРОФИЛЯ Дисциплина "Математическое моделирование процессов в компонентах природы"

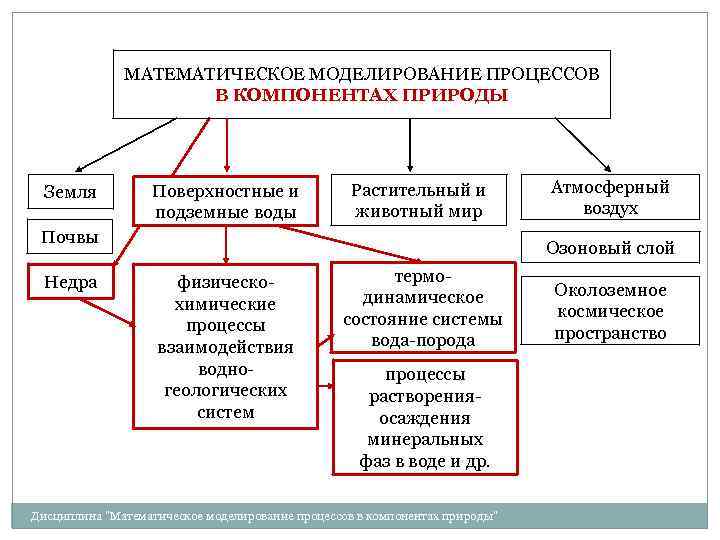МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ В КОМПОНЕНТАХ ПРИРОДЫ Земля Поверхностные и подземные воды Растительный и животный мир Почвы Недра Атмосферный воздух Озоновый слой физическохимические процессы взаимодействия водногеологических систем термодинамическое состояние системы вода-порода процессы растворенияосаждения минеральных фаз в воде и др. Дисциплина "Математическое моделирование процессов в компонентах природы" Околоземное космическое пространство

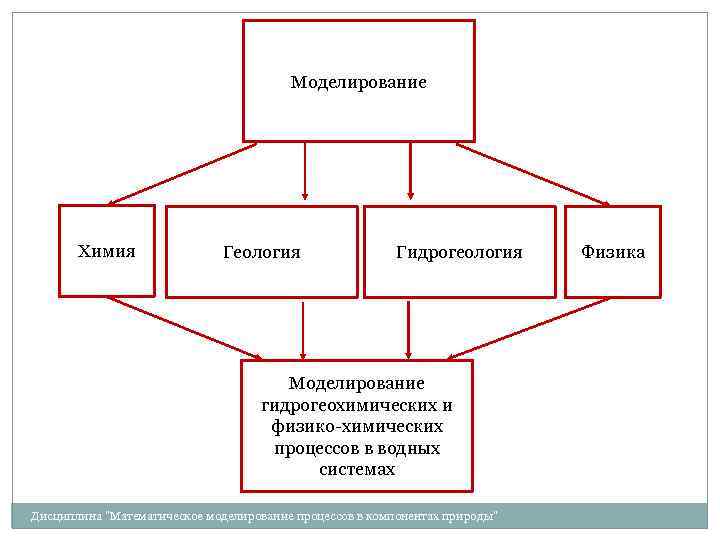Моделирование Химия Геология Гидрогеология Моделирование гидрогеохимических и физико-химических процессов в водных системах Дисциплина "Математическое моделирование процессов в компонентах природы" Физика

ЭТАПЫ РАЗВИТИЯ МЕТОДОВ МОДЕЛИРОВАНИЯ 8 В применении математических методов в гидрогеологии можно условно выделить четыре периода: I - начало ХIХ в. до 30 -х годов ХХ в. (единичные работы отдельных исследователей). II - 1930 -1965 гг. В это время началось широкое применение статистических и других математических методов в различных областях наук. III - после 1965 г. произошел качественный скачок в связи с появлением ЭВМ. Большие возможности ЭВМ в обработке гидрогеологической информации способствовали резкому расширению круга математических методов и решаемых с их помощью задач. IV - с 1990 г. оперативная обработка информации за счет доступности техники. Дисциплина "Математическое моделирование процессов в компонентах природы"

ОСНОВНЫЕ ПОНЯТИЯ 9 Материальные системы, как объекты изучения, разделяют на: • хорошо организованные (простейшие химические и физические процессы, механизмы, приборы и др. ) • плохо организованные (живые организмы и их сообщества, а также большинство объектов, изучаемых науками о Земле) Дисциплина "Математическое моделирование процессов в компонентах природы"

Модель — это мысленно представляемая или материально реализованная система, которая, отображая или воспроизводя объект исследования, способна замещать его так, что ее изучение дает об этом объекте новую информацию!!!! Математическая модель — это упрощенное описание реальности с помощью математических понятий. Дисциплина "Математическое моделирование процессов в компонентах природы" 10

Математическая модель может быть получена двумя методами: 1) на основе теоретического анализа процесса с использованием основных законов физики, химии и др. естественных наук; 2) на основе данных активного или пассивного эксперимента. Дисциплина "Математическое моделирование процессов в компонентах природы" 11

ТИПЫ ГЕОЛОГО-МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ 12 По характеру моделей выделяют: 1. предметное 2. знаковое (информационное) моделирование В зависимости от того, какие особенности объекта изучаются, различают: 1. модели структуры объекта 2. модели поведения (функционирования) объекта Дисциплина "Математическое моделирование процессов в компонентах природы"

По принципу построения математической модели различают: 1. статическое моделирование 2. динамическое моделирование По характеру связи между параметрами и свойствами изучаемых объектов математические модели разделяются на: 1. статистические 2. детерминированные Дисциплина "Математическое моделирование процессов в компонентах природы" 13

Статистическая модель – это математическое выражение, содержащее минимум одну случайную компоненту (переменную), значение которой нельзя предсказать точно для единичного наблюдения. Такие модели широко используют для целей математического моделирования, поскольку они хорошо учитывают случайные колебания экспериментальных данных. Дисциплина "Математическое моделирование процессов в компонентах природы" 14

МОДЕЛИРОВАНИЕ КАК МЕТОД ИССЛЕДОВАНИЯ 15 Моделирование подразделяют на: 1. физическое 2. математическое Физическое моделирование ‑ метод исследования, построенный на принципе сходства физической природы созданной модели с ее оригиналом и основанный на теории подобия. Дисциплина "Математическое моделирование процессов в компонентах природы"

Математическое моделирование – 1) это метод исследования объектов и процессов реального мира с помощью их приближенных математических описаний ‑ математических моделей, при котором физика исследуемого процесса при переходе к модели не сохраняется. 2) это идеальное научное знаковое формальное моделирование, при котором описание объекта осуществляется на языке математики, а исследование модели проводится с использованием тех или иных математических методов. Дисциплина "Математическое моделирование процессов в компонентах природы" 16

ПРЕИМУЩЕСТВА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ В СРАВНЕНИИ С НАТУРНЫМ ЭКСПЕРИМЕНТОМ 17 1. Экономичность (сбережение ресурсов реальной системы); 2. Возможность моделирования гипотетических, т. е. не реализованных в природе объектов (прежде всего на разных этапах проектирования); 3. Возможность реализации режимов, трудновоспроизводимых в натуре; опасных или 4. Возможность изменения масштаба времени; 5. Простота многоаспектного анализа; 6. Большая прогностическая сила вследствие возможности выявления общих закономерностей; 7. Универсальность технического и программного обеспечения проводимой работы. Дисциплина "Математическое моделирование процессов в компонентах природы"

Использование моделирования на эмпирическом и теоретическом уровнях исследования приводит к делению моделей и моделирования на: 1) Идеальные модели и идеальное моделирование 2) Материальные модели и материальное моделирование Идеальное моделирование является первичным по отношению к материальному – вначале в сознании исследователя формируется идеальная модель, а затем на ее основе строится материальная. Дисциплина "Математическое моделирование процессов в компонентах природы" 18

Идеальное моделирование разделяют на: 1. интуитивное (эвристическое) и 2. научное Интуитивное моделирование – это моделирование, основанное на интуитивном (не обоснованном с позиций формальной логики) представлении об объекте исследования, не поддающимся формализации или не нуждающимся в ней. Научное моделирование – это всегда логически обоснованное моделирование, использующее минимальное число предложений, принятых в качестве гипотез на основании наблюдений за объектом моделирования. Интуитивная первооснова любого знания присутствует всегда!!! Дисциплина "Математическое моделирование процессов в компонентах природы" научного 19

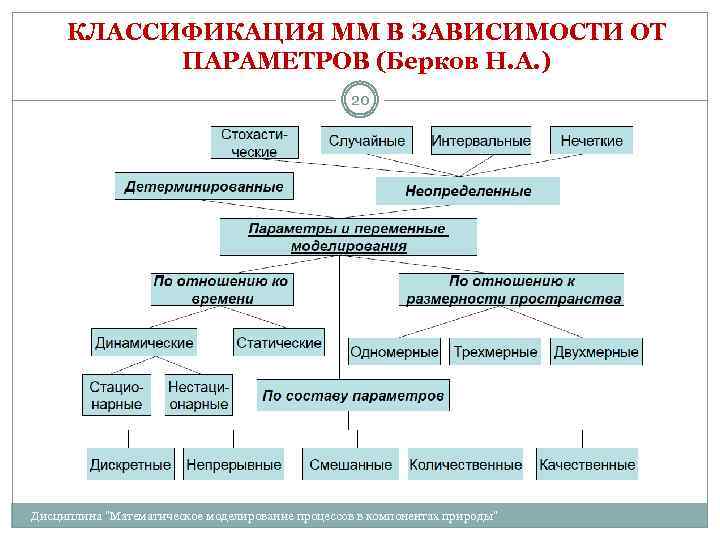КЛАССИФИКАЦИЯ ММ В ЗАВИСИМОСТИ ОТ ПАРАМЕТРОВ (Берков Н. А. ) 20 Дисциплина "Математическое моделирование процессов в компонентах природы"

ПОСТАНОВКА ЗАДАЧ МОДЕЛИРОВАНИЯ 21 Концептуальная постановка задачи моделирования – это сформулированный в терминах конкретной дисциплины (геологии, экологии, химии и т. д. ) перечень основных вопросов, интересующих исследователя или заказчика, а также совокупность гипотез относительно свойств и поведения объекта моделирования. Дисциплина "Математическое моделирование процессов в компонентах природы"

Математическая постановка задачи моделирования – это совокупность математических соотношений, описывающих поведение и свойства объекта моделирования. Они определяют вид оператора модели. Дисциплина "Математическое моделирование процессов в компонентах природы" 22

ЭТАПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКОЙ МОДЕЛИ (Берков Н. А. ) 23 Дисциплина "Математическое моделирование процессов в компонентах природы"

1 2 3 4 5 6 7 8 Блоки: 1 – система (объект, явление, процесс) 2 – описание системы 3 – постановка задачи 4 – математическая модель 5 – непротиворечивость выводов в рамках модели 6 – решение задачи 7 – проверка адекватности 8 – уточнение модели При изучении любого объекта путем моделирования нужно выполнять ряд обязательных, вышеперечисленных этапов. Дисциплина "Математическое моделирование процессов в компонентах природы" 24

1 Дуги: 2 Дуга (1 – 2) – наблюдение эксперимента Дуга (2 – 3) – формализация абстракции Дуга (3 – 4) – конструирование элементов модели Дуга (4 – 5) – изучение модели Дуга (5 – 6) – выбор методов решения Дуга (6 – 7) – сравнение выводов с реальными фактами 3 4 5 6 7 8 Дисциплина "Математическое моделирование процессов в компонентах природы" 25

ОСНОВНЫЕ ПРИНЦИПЫ ПОСТРОЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ (по Ю. Ю. Тарасевичу) 26 1. Принцип простоты: не стоит решать сложную задачу, не решив простую; 2. Принцип А. А. Андронова: без ошибки нет модели, а потому негрубые модели (структурно-неустойчивые) – плохие; 3. Принцип Э. Хемингуэя: можно пренебрегать чем угодно, нужно только точно знать, как это повлияет на результат; 4. Принцип надежности: чем проще модель, тем она реже обманывает; 5. Принцип А. Н. Крылова: точность результатов не может быть выше точности исходных данных; точности промежуточных данных должны быть согласованы; 6. Цель расчетов – не числа, а понимание. Прежде чем решать задачу, подумай, что делать с ее решением (законы Р. В. Хемминга, 1972) Дисциплина "Математическое моделирование процессов в компонентах природы"

ПРИНЦИПЫ ОПИСАНИЯ ПРИРОДНО-ТЕХНОГЕННЫХ ФИЗИКО-ХИМИЧЕСКИХ СИСТЕМ 27 Термодинамическая (физико-химическая) система - в геологии и геохимии под ней понимается мысленно выделенная часть геологической или иной среды, которая подвергается изучению. Такой системой может быть: üЗемля или другое космическое тело; üземная кора; üконкретная геологическая структура или геологический объект, вне зависимости от их размеров; üместорождение (урана, цветных металлов и др. ), üчасть продуктивного пласта; üучасток нефте- и водопровода; üпробирка с пробой пластовой воды, раствором кислоты и щелочи, образец породы и т. д. Дисциплина "Математическое моделирование процессов в компонентах природы"

За границами системы располагается внешняя по отношению к ней среда, с которой: 1. Открытая система может обмениваться веществом (В), теплом (Q) и энергией (E); 2. Закрытая система - только Q и E; 3. Изолированная система не имеет возможности к обмену с окружающей средой ничем: В, Q, Е; 4. Динамическая система эволюционизирующая (меняющаяся) во времени система (синергетическое понятие). Полностью изолированных (идеальных) систем в природе не существует. Это понятие введено с целью упрощения описания реальных систем и используется для случаев, когда массо- и энергообменом с окружающей средой, ввиду их малой величины или интенсивности протекания, можно пренебречь. Дисциплина "Математическое моделирование процессов в компонентах природы" 28

Составляющими системы обычно являются одна или несколько фаз. Фаза – это физически самостоятельные части, отделенные друг от друга поверхностью раздела. Существует: твердая фаза – порода, жидкая фаза – вода или нефть, газообразная фаза – природные и иные газы и их смеси. Каждая из фаз может включать один или несколько компонентов, представляющих собой относительно устойчивое химическое соединение, например: üминерал породы, üрастворитель (вода) и ионы, üионные ассоциаты и молекулы растворенного вещества в водных растворах, üмолекулы органических и неорганических соединений, индивидуальные газы (в том числе пары воды). Дисциплина "Математическое моделирование процессов в компонентах природы" 29

Любой из выделенных систем присуще определенное физикохимическое или термодинамическое состояние, характеризуемое набором параметров: üтемпературой, üдавлением, üмассой фаз и их составляющих, üхимическим составом, а также üсамопроизвольным эволюционным развитием, которое может чередоваться со скачкообразными (революционными) изменениями качественного состояния, направленного на восстановление состояния равновесия между внутренними частями системы и между системой и ее окружением. Индивидуальные свойства каждого из компонентов системы описываются с помощью ограниченного набора их стандартных термодинамических параметров. Дисциплина "Математическое моделирование процессов в компонентах природы" 30

Текущее состояние системы определяют как текущее местоположение компонентов системы на пути ее перехода от начального состояния к состоянию равновесия. Состояние равновесия определяется внешними условиями и балансом вещества и энергии, которое устанавливается расчетным путем или экспериментально. Самопроизвольное развитие подчиняется исключительно законам равновесной термодинамики. То есть оно может быть только однонаправленным и должно всегда сопровождаться ростом энтропии. Энтропия (от греческого – поворот, превращение) – количественная мера неопределенности ситуации, упорядоченности системы и ее способности пребывать в данном состоянии. Зависит от способности энергии к превращениям и направленности этих превращений. Дисциплина "Математическое моделирование процессов в компонентах природы" 31