ЛЕКЦИЯ 1 МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 1 Основные положения

ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 1. Основные положения молекулярнокинетической теории вещества

Молекулярная физика – раздел физики, изучающий физические свойства вещества на основе рассмотрения его молекулярного строения

Основные положения МКТ: 1. Все тела – твердые, жидкие, газообразные – состоят из атомов и молекул. 2. Молекулы всех тел находятся в беспорядочном хаотическом движении, не имеющем какого-либо выбранного направления; такое движение называется тепловым, т. к. его скорость зависит от температуры вещества.

Молекула – наименьшая частица вещества, определяющая все его химические свойства; молекула состоит из атомов. Атом – наименьшая частица химического элемента, способная к самостоятельному существованию и являющаяся носителем его индивидуальных свойств.

Вероятностный метод в молекулярной физике Молекулярная физика пользуется вероятностными (статистическими) методами и объясняет наблюдаемые на опыте свойства тел суммарным результатом действия отдельных молекул; поэтому молекулярная физика часто называется статистической физикой

ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 2. Масса и размеры молекул

Атомная единица массы (а. е. м) – единица измерения массы атомов и молекул. 1 а. е. м. называется масса, равная 1/12 массы атома 12 С (изотопа углерода с массовым числом 12): 1 а. е. м. = 1, 66 10 -27 кг

Относительная атомная масса Относительной атомной массой Ar химического элемента называется отношение массы атома этого элемента к 1 а. е. м.

Относительная молекулярная масса Относительной молекулярной массой Mr вещества называется отношение массы молекулы этого вещества к 1 а. е. м.

Количество вещества Моль (единица измерения количества вещества в МКТ) – количество вещества, в котором содержится столько структурных единиц (атомов, молекул, ионов, кластеров, электронов и т. д. ), сколько атомов содержится в 12 г изотопа углерода 12 С.

Число Авогадро NA – число частиц а одном моле вещества:

Молярная масса Молярной массой M называется масса одного моля вещества: Молярная масса, выраженная в граммах на моль, численно равна относительной молекулярной массе: M = Mr (г/моль)

ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 3. Модель идеального газа

Идеальный газ Идеальным газом называется газ, молекулы которого: ▪ не взаимодействуют друг с другом на расстоянии (при столкновении друг с другом и со стенками сосуда молекул ведут себя как абсолютно упругие шары). ▪ Собственный объем молекул газа ничтожно мал по сравнению с объемом сосуда, в котором находится газ.

Уравнение состояния идеального газа (уравнение Менделеева – Клапейрона):

Уравнение состояния идеального газа

Закон Авогадро В одинаковых объемах идеальных газов при одинаковых температурах и давлении содержится одно и то же число молекул (верно и обратное утверждение: различные газы, содержащие одинаковое число молекул, при одинаковых температуре и давлении занимают одинаковые объемы). В частности, при нормальных условиях (T 0 = 273, 15 K, p 0 = 1, 0132 105 Па) 1 моль любого газа занимает объем Vm = 22, 415 10 -3 м 3

Плотность идеального газа

Закон Дальтона Давление смеси идеальных газов равно сумме парциальных давлений этих газов: Парциальным давлением компоненты газовой смеси называется давление, которые производила бы она, если бы занимала весь объем смеси в отсутствии других компонент При этом каждая и газовая компонента смеси подчиняется уравнению Менделеева – Клапейрона.

Уравнение состояния для смеси идеальных газов

ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 4. Основное уравнение молекулярнокинетической теории

Основное уравнение МКТ Основное уравнение молекулярнокинетической теории газов связывает давление p, оказываемое газом на стенки сосуда, со средней кинетической энергией поступательного движения молекулы < пост>:

Предположения, при которых получено основное уравнение МКТ: Газ находится в состоянии термодинамического равновесия со стенками сосуда; давление газа не зависит от формы и размеров сосуда. Взаимодействие молекул со стенками сосуда описывается моделью упругих соударений с зеркальным отражением. Все направления движения молекул равновероятны.

ЛЕКЦИЯ 1. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ВЕЩЕСТВА 5. Распределение энергии по степеням свободы молекул

Число степеней свободы Числом степеней свободы механической системы называется число независимых величин, полностью определяющих положение системы в пространстве. Степени свободы молекул идеального газа могут быть поступательными (т. е. соответствовать поступательному движению), вращательными и колебательными

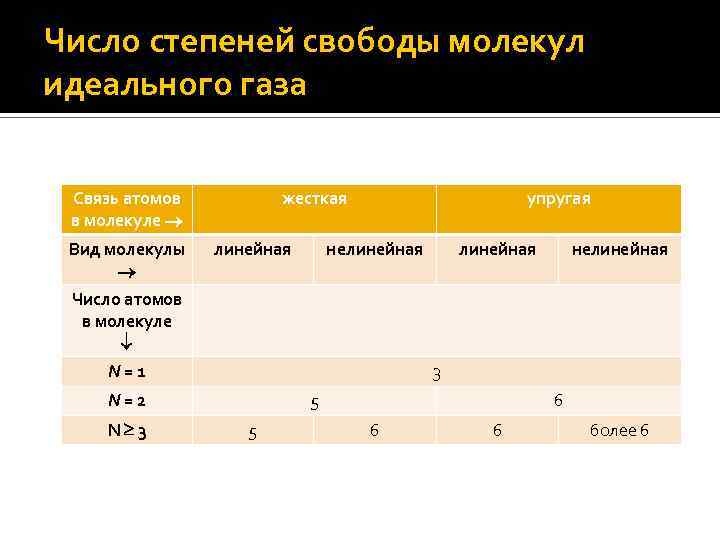Число степеней свободы молекул идеального газа Связь атомов в молекуле Вид молекулы жесткая линейная упругая линейная нелинейная Число атомов в молекуле N=1 3 N=2 N 3 5 5 6 6 6 более 6

Закон Больцмана (закон равнораспределения энергии по степеням свободы): в состоянии теплового равновесия на каждую степень свободы в среднем приходится одинаковая энергия, равная (½)k. T

Упругая молекула (молекула, атомы которой совершают колебания), обладает как кинетической, так и потенциальной энергией, связанной с колебаниями, поэтому колебательная степень свободы характеризуется удвоенной энергетической емкостью: средняя энергия, приходящаяся на колебательную степень свободы, равна k. T (по (1/2)k. T на кинетическую и на потенциальную энергии колебаний)

Эффективное число степеней свободы

Средняя энергия одной молекулы и N молекул