Лекция № 1 Линейное программирование
Введение В основе любой целенаправленной деятельности лежат процессы принятия решений. В экономике они предшествуют созданию производственных и хозяйственных организаций, обеспечивают их оптимальное функционирование и взаимодействие. Оптимальные решения позволяют достигать цели при минимальных затратах трудовых, материальных и сырьевых ресурсов. Поиск оптимальных решений неразрывно связан с нахождением экстремумов так называемых производственных (целевых) функций. Дисциплина Методы оптимальных решений является одним из разделов кибернетики , использующим для решения задач методы математического программирования.
Введение Широкий класс экономических задач составляют такие экстремальные задачи, в математических моделях которых значения переменных задаются равенствами и неравенствами. Теория и методы решения таких задач как раз и составляют содержание математического программирования. Если целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств, то в этом случается говорят о линейном математическом программировании. В противном случае используется нелинейное математическое программирование.
Линейное программирование Задача линейного программирования заключаются в нахождении максимума (минимума) некоторой линейной функции, называемой целевой функцией F. при условиях: Совокупность графиков равенств и неравенств, задающих множество допустимых значений независимых переменных, а также графика целевой функции, образуют многогранник решений, всякая угловая точка которого называется вершиной решений. Если задача линейного проектирования имеет оптимальный план, максимальное (минимальное) значение целевая функция принимает в одной из вершин многогранника решений. Если максимальное (минимальное) значение целевая функция принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой
Графическое решение задач линейного программирования Из вышесказанного следует, что задачи линейного программирования могут быть решены графически, при построении многоугольников решений в соответствии с заданными условиями. Для нахождения среди допустимых решений оптимального, используют линии уровня и опорные прямые. Линией уровня называется прямая, но которой целевая функция принимает постоянное значение: Все линии уровня нормальным вектором параллельны другу. Значения целевой функции на линиях уровня возрастают, если линии ровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.
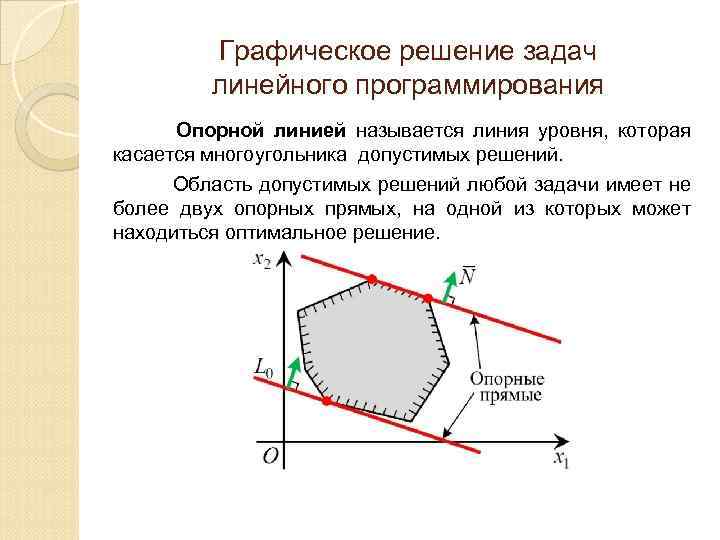Графическое решение задач линейного программирования Опорной линией называется линия уровня, которая касается многоугольника допустимых решений. Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
Алгоритм графического решение задач линейного программирования с двумя переменными 1. Строим область допустимых решений для заданной системы ограничений. Если ОДР – пустое множество, то задача неразрешима ввиду несовместности ограничений. 2. Если ОДР является непустым множеством, строим вектор нормали 3. Проводим линию уровня перпендикулярную вектору . 4. Линию перемещаем до положения опорной прямой в направлении вектора для задач на максимум и в противоположном направлении для задач на минимум. Общая точка (точки) будет точкой экстремума (оптимума) целевой функции в ОДР. 5. Находим координаты точки экстремума и значение целевой функции.
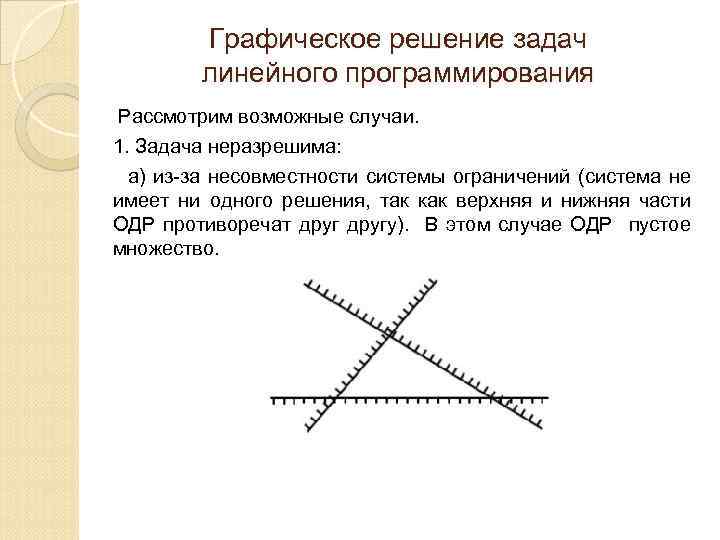Графическое решение задач линейного программирования Рассмотрим возможные случаи. 1. Задача неразрешима: а) из-за несовместности системы ограничений (система не имеет ни одного решения, так как верхняя и нижняя части ОДР противоречат другу). В этом случае ОДР пустое множество.
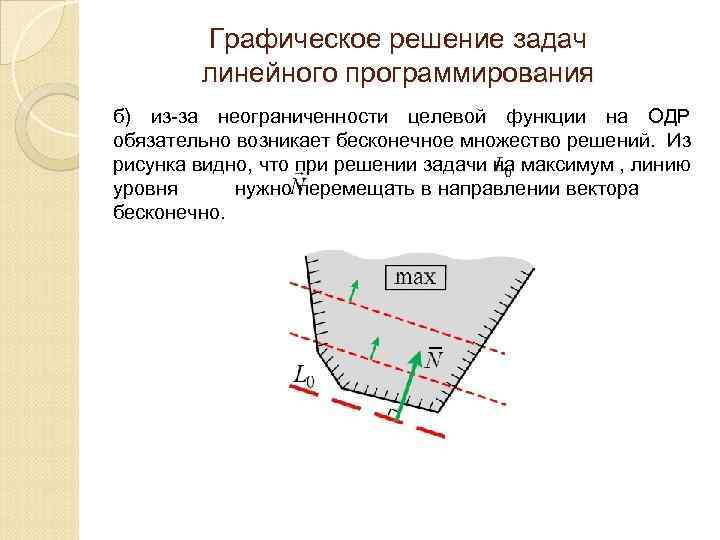Графическое решение задач линейного программирования б) из-за неограниченности целевой функции на ОДР обязательно возникает бесконечное множество решений. Из рисунка видно, что при решении задачи на максимум , линию уровня нужно перемещать в направлении вектора бесконечно.
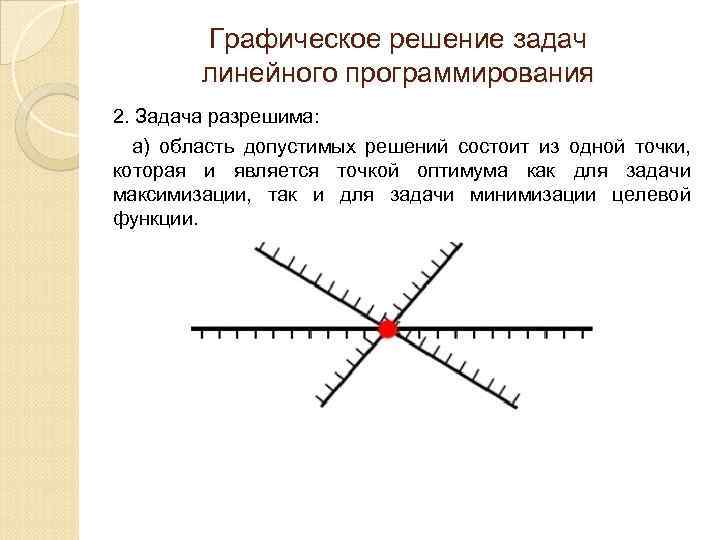Графическое решение задач линейного программирования 2. Задача разрешима: а) область допустимых решений состоит из одной точки, которая и является точкой оптимума как для задачи максимизации, так и для задачи минимизации целевой функции.
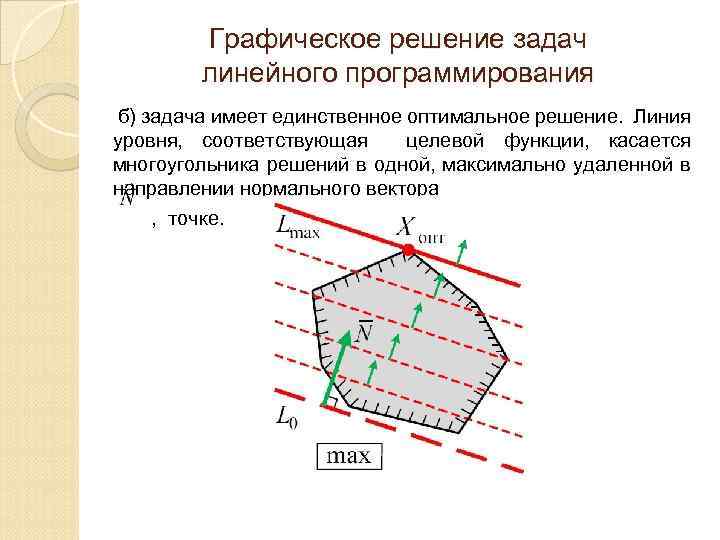Графическое решение задач линейного программирования б) задача имеет единственное оптимальное решение. Линия уровня, соответствующая целевой функции, касается многоугольника решений в одной, максимально удаленной в направлении нормального вектора , точке.
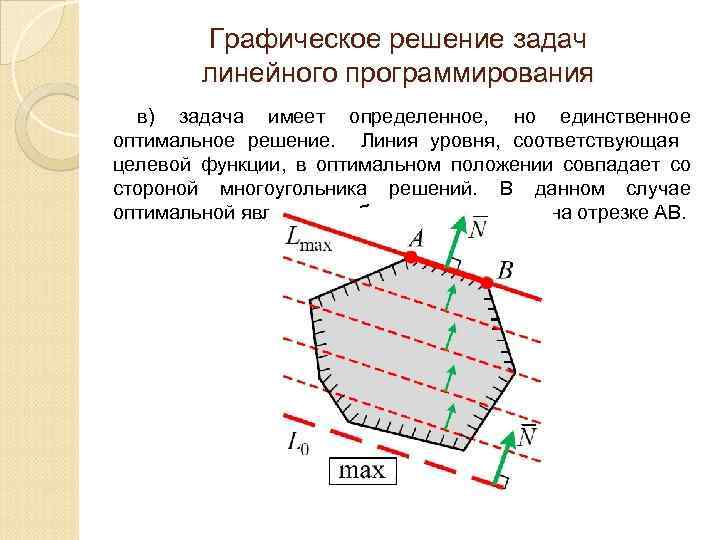Графическое решение задач линейного программирования в) задача имеет определенное, но единственное оптимальное решение. Линия уровня, соответствующая целевой функции, в оптимальном положении совпадает со стороной многоугольника решений. В данном случае оптимальной является любая точка, лежащая на отрезке АВ.
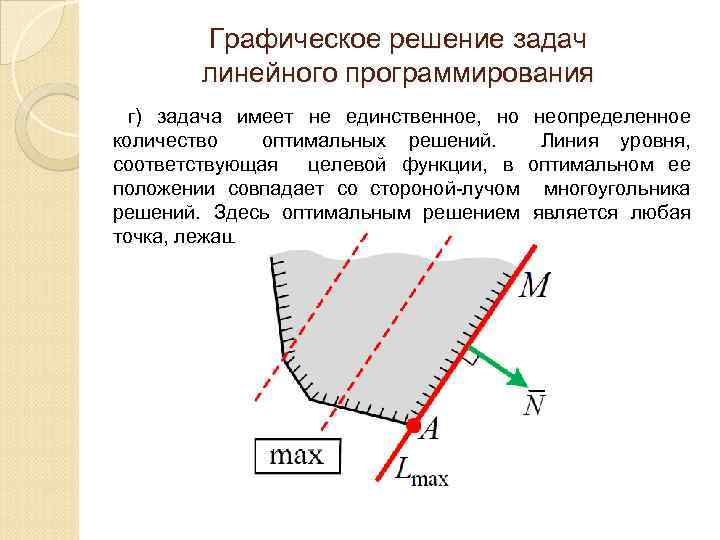Графическое решение задач линейного программирования г) задача имеет не единственное, но неопределенное количество оптимальных решений. Линия уровня, соответствующая целевой функции, в оптимальном ее положении совпадает со стороной-лучом многоугольника решений. Здесь оптимальным решением является любая точка, лежащая на луче АМ.
Графическое решение задач линейного программирования Рассмотрим графическое решение задачи на конкретном примере. Задача 1. Найти максимум целевой функции при ограничениях: и Решение. 1. Изобразим на плоскости систему координат
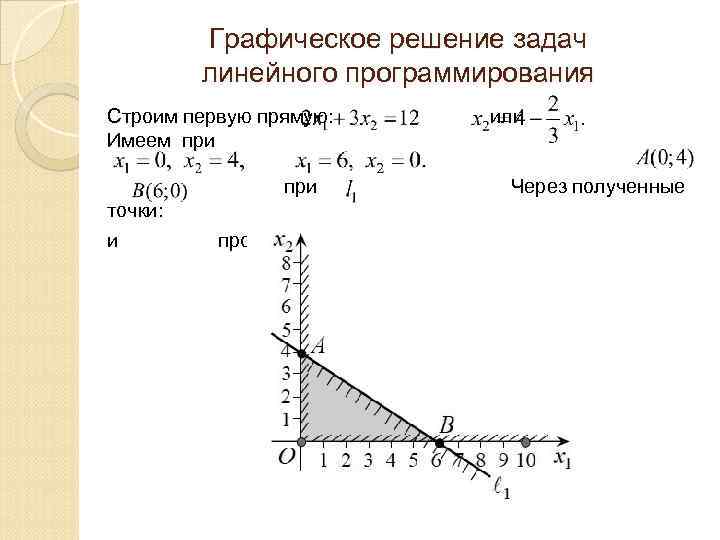Графическое решение задач линейного программирования Строим первую прямую: Имеем при или при точки: и провидим прямую Через полученные.
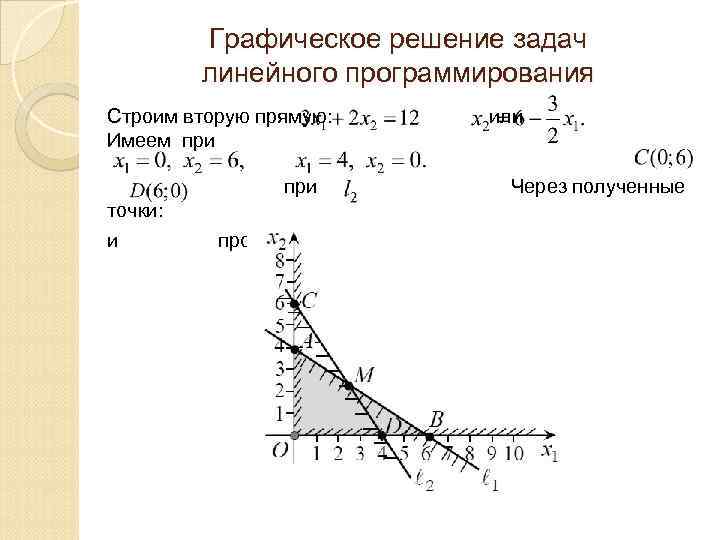Графическое решение задач линейного программирования Строим вторую прямую: Имеем при или при точки: и провидим прямую Через полученные.
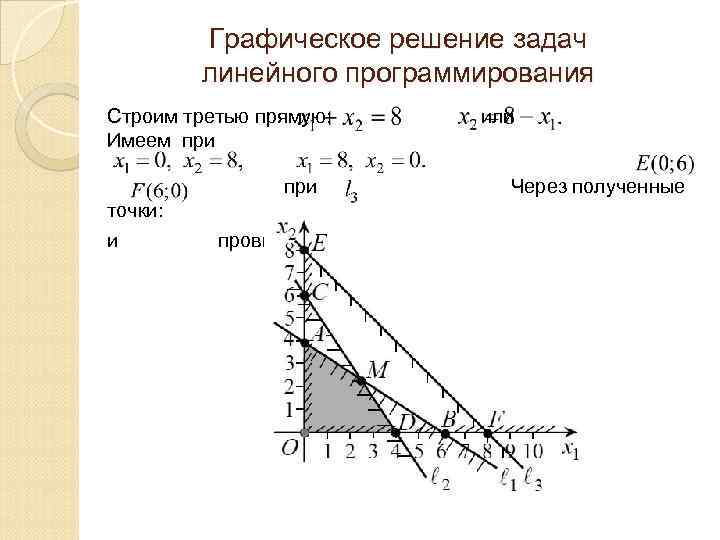Графическое решение задач линейного программирования Строим третью прямую: Имеем при или при точки: и провидим прямую Через полученные.
СПАСИБО ЗА ВНИМАНИЕ!