5_prezentatsia.ppt
- Количество слайдов: 21
![ЛЕКЦИЯ 1 Исторический обзор развития оснований геометрии. История попыток доказательства пятого постулата. Литература [1] ЛЕКЦИЯ 1 Исторический обзор развития оснований геометрии. История попыток доказательства пятого постулата. Литература [1]](https://present5.com/presentation/-76488752_416593334/image-1.jpg)
ЛЕКЦИЯ 1 Исторический обзор развития оснований геометрии. История попыток доказательства пятого постулата. Литература [1] § 67 ‑ 70, [2] § 8

Фалес Милетский (635 - 548 г. г. до нашей эры) Свойства вертикальных углов, углов при основании равнобедренного треугольника, свойств отрезков, отсекаемых параллельными прямыми от сторон угла и ряд других утверждений

Пифагор (570 - 471 г. г. до нашей эры) Были доказаны свойства суммы углов треугольника, геометрический способ решения квадратных уравнений, знаменитая теорема Пифагора, существование несоизмеримых отрезков, пяти типов правильных многогранников, экстремальные свойства круга и шара.

Евклид (около 330 - 275 г. г. до нашей эры) В основу “Начал” Евклид положил определения, сформулировал аксиомы и постулаты, а затем логически безупречно выводил из них остальные предложения, описывающие геометрические свойства плоских фигур и пространственных тел

Некоторые определения первой книги • Точка есть то, что не имеет частей. • Линия есть длина без ширины. • Концы линии суть точки. • Прямая линия есть та, которая одинаково лежит относительно всех своих точек. • Поверхность есть то, что имеет только длину и ширину. • Концы же или края поверхности суть линии. • Плоская поверхность есть та, которая одинакова расположена относительно всех своих прямых.

Аксиомы 1. Равные одному и тому же третьему также равны между собой. 2. Если к равным прибавить равные, то и целые будут равны. 3. Если от равных отнять равные, то полученные остатки будут равны. 4. Совмещающиеся друг с другом равны. 5. Целое больше своей части.

Постулаты Требуется, чтобы: 1. От каждой точки до другой можно было провести прямую. 2. Ограниченную прямую можно было продолжит неограниченно в любую сторону. 3. Из любого центра можно было описать окружность любым радиусом. 4. Все прямые углы были равны между собой. 5. Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны.
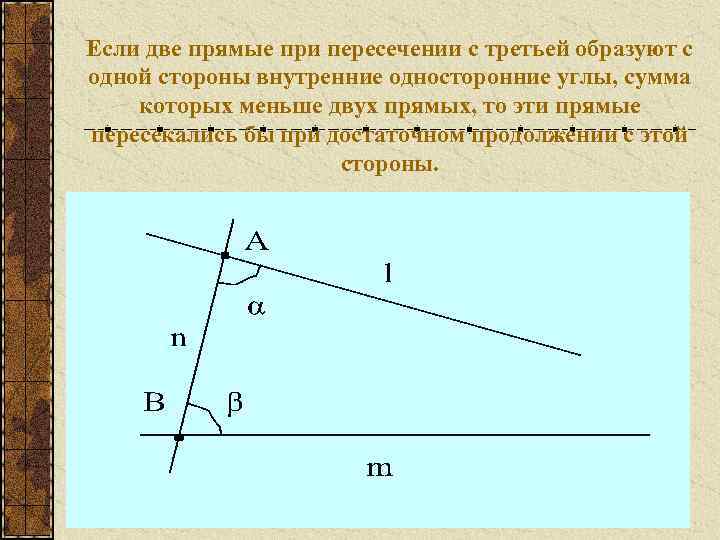
Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны.

Посидоний (около 135 – 50 годы до нашей эры) Параллельными называются такие прямые, которые находятся в одной плоскости, не сближаются и не удаляются, так, что все перпендикуляры, проведенные к одной из них из точек другой, равны между собой

Доказательство Прокла (410 – 475 годы нашей эры) Два неявных допущения: расстояние от одной стороны угла до другой, по мере удаления от вершины, неограниченно возрастает; расстояние между двумя непересекающимися прямыми на плоскости ограничено.

Омар Хайям (1048 - 1131) Посвятил теории параллельных линий первую книгу своих “Комментариев к трудностям во введениях книги Евклида”.

Четырехугольник Саккери Теория параллельных линий Хайяма была первой в истории, в которой пятый постулат доказывался не на “постулировании основания”, а при использовании другого, более наглядного предположения

Джон Валлис (1616 - 1703) В своем трактате «О пятом постулате и пятом определении в книге Евклида, геометрическое рассуждение» приводит свое доказательство пятого постулата Евклида. При этом он вводит следующий постулат: «Для всякой фигуры возможна подобная ей фигура произвольной величины» .

Джироламо Саккери (1667 – 1773) В 1773 году в Милане была издана книга «Евклид, очищенный от всяких пятен, или геометрическая попытка установить самые первые начала всей геометрии» . Саккери рассматривает тот же четырехугольник с равными боковыми сторонами и двумя прямыми углами при основании, что и Омар Хайям. Опровергнув гипотезу тупого угла и доказав, что гипотеза прямого угла равносильна пятому постулату Евклида, Саккери исследует гипотезу острого угла и получает достаточно много утверждений, справедливых в геометрии Лобачевского.

Иоганн Генрих Ламберт (1728 - 1777) Наиболее важными из его результатов являются следующие: если имеет место гипотеза острого угла, то сумма углов треугольника меньше двух прямых углов, существует абсолютная мера измерения отрезков и площадей фигур, отсутствует подобие. Исследуя аналогии, которые возникают при доказательствах соответствующих утверждений при гипотезах тупого и острого углов, Ламберт делает поразительное заключение: «Я почти должен был бы сделать вывод, что третья гипотеза (гипотеза острого угла) имеет место на некоторой мнимой сфере. По меньшей мере, должно же быть что-то, из-за чего она на плоскости так долго не дает себя опровергнуть, как это имело место при второй гипотезе (гипотезе тупого угла)» .

Адриан Мари Лежандр – (1753 – 1833 г. г. ) Без использования пятого постулата и его следствий, Лежандр доказал, что сумма углов треугольника не может превышать двух прямых углов и, если сумма углов какого либо треугольника равна двум прямым, то тогда на плоскости сумма углов любого другого треугольника также совпадает с двумя прямыми углами и, следовательно, выполняется условие пятого постулата Евклида.

Николай Иванович Лобачевский (1793 - 1856) В 1829 году он опубликовал свои результаты в работе «О началах геометрии» . Заменив аксиому параллельности евклидовой геометрии ее отрицанием, Н. И. Лобачевский построил геометрическую теорию, названную им «Воображаемой геометрией» . На протяжении тридцати лет им было опубликовано несколько трудов, в которых развивались идеи, заложенные в первой работе, и искались ее приложения к другим областям математики.

Янош Бояи (1802 - 1860) Если сравнивать труды Н. И. Лобачевского и «Аппендикс» Я. Бояи, то можно сказать, что Лобачевский продвинулся в изучении геометрических свойств нового пространства существенно дальше и первым опубликовал свои результаты. Поэтому приоритет Н. И. Лобачевского здесь бесспорен. Хотя в трудах Я. Бояи содержатся исследования по геометрическим свойствам треугольников и так называемым «предельным кривым» , которые гораздо глубже соответствующих исследований, опубликованных Лобачевским

Карл Фридрих Гаусс (1777 - 1855) «Весь путь, по которому твой сын пошел, и результаты, которые он получил, сплошь совпадают с моими собственными, имеющими частично давность в 30 - 35 лет. Я, действительно, этим в высшей степени поражен. Мои намерения были ничего при жизни не публиковать о моей собственной работе, которая, впрочем, до настоящего времени мало нанесена на бумагу» .
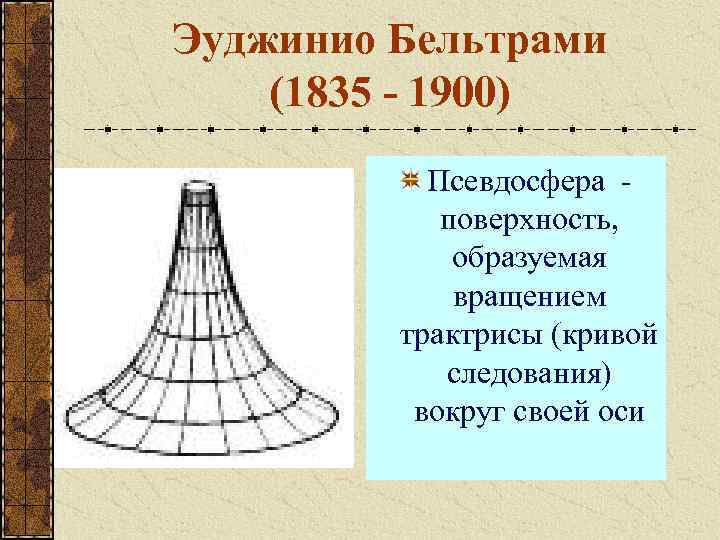
Эуджинио Бельтрами (1835 - 1900) Псевдосфера поверхность, образуемая вращением трактрисы (кривой следования) вокруг своей оси

Феликс Клейн (1849 -1925)
5_prezentatsia.ppt