Лекция 1 Экономико-математические методы и модели Денисова С

Лекция 1. Экономико-математические методы и модели. Денисова С. Т. Старший преподаватель кафедры ММи. МЭ 1

План: 1. Основные понятия: моделирование, математическая модель, схема модели, требования к модели. l 2. Классификация экономико-математических моделей. l 3. Примеры экономико-математических моделей. l 2

Основные понятия l Модель – условный образ объекта или процесса, адекватно отображающий исследуемую систему. l Моделирование – замещение одного исходного объекта или процесса другим объектом, называемым моделью (рис. 1. 1), и проведение экспериментов с моделью с целью получения информации о системе путем исследования свойств модели. 3

Основные понятия Система (от греч. systema – целое, составленное из частей; соединение) – совокупность взаимосвязанных элементов, объединенных в одно целое для достижения некоторой цели, определяемой назначением системы. l Математическая модель – математическое описание исследуемого процесса или объекта. l 4

Основные понятия Структура системы задается перечнем элементов, входящих в состав системы, и связей между ними. l Процесс (от лат. processus – продвижение) – последовательная смена состояний системы во времени или случайная смена состояний. l Состояние системы задается совокупностью значений переменных, описывающих это состояние. l 5

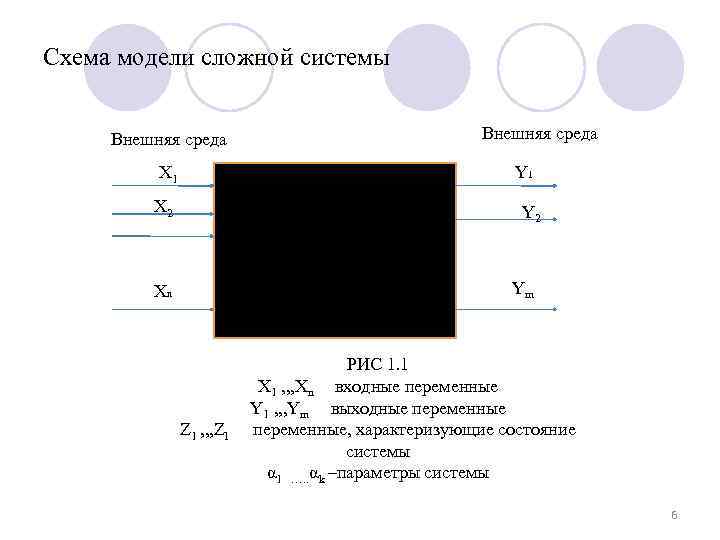Схема модели сложной системы Внешняя среда Y 1 X 1 СИСТЕМА α 1 α 2…. αk X 2 Y 2 Z 1 Z 2 …Z 1 Ym Xn Z 1 , , , Zl РИС 1. 1 X 1 , , , Xn входные переменные Y 1 , , , Ym выходные переменные, характеризующие состояние системы α 1 …. . αk –параметры системы 6

Основные требования к модели: l l l l l простота модели; адекватность исследуемой системе. Простота модели обусловлена необходимостью построения модели, которая может быть рассчитана доступными методами. Адекватность (от лат. adaequatus – приравненный, равный) –соответствие модели оригиналу, характеризуемое степенью близости свойств модели свойствам исследуемой системы зависит от: степени полноты и достоверности сведений об исследуемой системе; уровня детализации модели. Моделирование может проводиться: в условиях полной определенности, означающей наличие точной информации обо всех исходных параметрах; в условиях неопределенности, обусловленных: неточностью сведений о параметрах; отсутствием 7 сведений о значениях некоторых параметров.

Классификация экономико-математических моделей Математические модели, используемые в экономике, можно подразделить на классы по ряду признаков, относящихся к особенностям моделируемого объекта, цели моделирования и используемого инструментария: модели макро- и микроэкономические, балансовые, эконометрические, оптимизационные, сетевые, систем массового обслуживания, имитационные (экспертные). l По учёту фактора времени различают статические и динамические модели. l 8

В статических моделях экономическая система описана применительно к одному определённому моменту времени Динамические модели описывают экономическую систему в развитии. l По учёту фактора неопределённости различают: l Детерминированные (с однозначно определёнными результатами) l и стохастические( с различными вероятностными результатами) l 9

Экономико-статистическое моделирование осуществляется в следующем порядке: 1) определение цели решаемой задачи, экономический анализ и выявление факторов, влияющих на целевой результат; 2) определение математической формы связи независимых переменных (факторов) и результата; 3) сбор необходимых данных и их обработка; 4) вычисление параметров экономико-статистической модели; 5) анализ полученных данных, экономическая оценка и интерпретация модели. l Экономико-статистические модели могут быть представлены в виде производственных функций. 10

Примеры экономико-математических моделей Составление проектов землеустройства l Задача 1: Установить координаты местоположения фермы, при которых затраты на транспортировку кормов будут минимальными. Объём работ f по перемещению грузов Pi от заданных точек M(xi , yi) можно выразить формулой: f= Pi Ri , где Ri – расстояние перевозки; Pi – масса перевозимого груза. Выразив R через координаты, получим задачу нелинейного программирования: 11

2. Задача сельскохозяйственного предприятия l l l В сельскохозяйственном предприятии имеется 800 тыс. руб. , которые можно затратить на трансформацию кустарника в пашню и на получение урожая зерновых на этих площадях. Денежные затраты на освоение 1 га под пашню оценивают в 15 тыс. руб. , а на увеличение урожайности на 1 ц с 1 га – в 3 тыс. руб. Обозначим через х1 – площадь трансформируемых земель, х2 – урожайность зерновых. Количество произведённой продукции в стоимостном выражении связано с переменными х1, х2 следующей функцией: Z=5 х1 х2+10 х2. Требуется определить такие значения х1 и х2 , чтобы Z было максимальным. 12

Экономико-математическая модель задачи: l Z=5 х1 х2+10 х2 →max 15 х1+3 х2 = 800; x 1 ≥ 0 , x 2 ≥ 0. Задача нелинейного программирования. 13

Задача 3: Предприниматель решил выделить на расширение своего дела 150 тыс. руб. известно, что если на приобретение нового оборудования затратить х тыс. руб. , а на зарплату вновь принятых работников у тыс. руб. , то прирост объёма продукции составит Q=0. 001 x 0. 6·y 0. 4. l Как следует распределить выделенные денежные ресурсы, чтобы прирост объёма продукции был максимальным? l 14

Экономико-математическая модель: l l l l Целевая функция имеет вид: 0. 001 x 0, 6·y 0, 4 →max при ограничениях: x+y≤ 150, x≥ 0 , y ≥ 0 Задача нелинейного программирования. 15

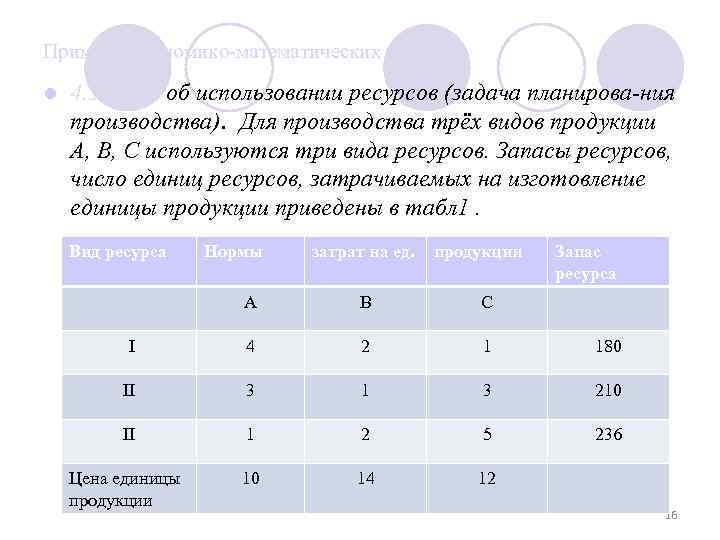Примеры экономико-математических моделей l 4. Задача об использовании ресурсов (задача планирова-ния производства). Для производства трёх видов продукции А, В, С используются три вида ресурсов. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции приведены в табл 1. Вид ресурса Нормы затрат на ед. продукции Запас ресурса A B C I 4 2 1 180 II 3 1 3 210 II 1 2 5 236 Цена единицы продукции 10 14 12 16

Необходимо составить такой план производства продукции, при котором прибыль от её реализа-ции будет максимальной. Экономико-математическая модель задачи ЛП: х1 – число единиц продукции вида А, l х2 – число единиц продукции вида В, l х3– число единиц продукции вида С, l F= 10 x 1+14 x 2+12 x 3→max (суммарная стоимость) l l l При ограничениях 4 х1+2 х2+х3≤ 180 3 х1+х2+3 х3≤ 210 х1+2 х2+5 х3≤ 236 x 1 ≥ 0 , x 2 ≥ 0, x 3 ≥ 0 17

Задача 5 ( задача землеустройства в с/х) l В хозяйстве имеется 200 га неиспользуемых земель , пригодных для освоения под пашню и сенокос. Затраты труда на освоение 1 га земель под пашню составляют 200 чел. -ч. , в сенокос – 50 чел. -ч. Для вовлечения земель в с/х –ый оборот предприятие может затратить не более 15000 чел. -ч. механизированного труда. Стоимость продукции, получаемой с 1 га пашни, составляет 800 руб. , с 1 га сенокосов – 300 руб. В задании на проектирование установлено, что площадь земель, осваиваемых под пашню, не должна превышать 2/3 площади сенокосов. Требуется определить, какую площадь необходимо освоить под пашню и сенокосы, чтобы получить максимальное количество продукции в стоимостном выражении. 18

Введём следующие обозначения: l l l х1 – площадь, трансформируемая в пашню, га; Х 2 –площадь, трансформируемая в сенокос, га. Целевая функция: F(x 1, x 2 )=800 x 1+300 x 2→max Ограничения: x 1+x 2≤ 200; (общее кол-во земли) 200 x 1+50 x 2≤ 15000; (трудовые ресурсы) 2/3 x 2 ≥ x 1; (соотношение площадей пашни и сенокосов) (или x 1 - 0, 667 x 2 ≤ 0 ) x 1 ≥ 0; x 2 ≥ 0 Задача линейного программирования. 19

Задача 6. Оптимальное использование рабочих агентов l Торговая фирма продаёт товары в n различных городах, покупательная способность жителей которых оценивается bj у. е. J=1, 2, . . n. Для реализации товаров фирма располагает n торговыми агентами, каждого из которых она направляет в один из городов. Профессиональный уровень агентов различен. Доля реализуемых i-м торговым агентом покупательных способностей составляет ai , i=1, 2, . . n. Как следует распределить торговых агентов по городам, чтобы фирма получила максимальную выручку от продажи товаров? (Ограничения: В каждый город направляется 1 торговый агент, и один торговый не может работать в 2 -х городах) 20

Экономико-математическая модель l ci j = ai bj - характеризует величину покупательных способностей, реализуемых i-м торговым агентом в j-м городе. Введём 21

Общая задача математического программирования Найти максимум (минимум) функции y=f(x 1, x 2, …, хn), l при условии, что независимые переменные x 1, x 2, …, хn удовлетворяют системе ограничений: l g 1(x 1, x 2, …, хn) ≤b 1, l …………… l gk(x 1, x 2, …, хn) ≤bk, l gk+1(x 1, x 2, …, хn) =bk+1, l …………… l gp(x 1, x 2, …, хn) =bp, 22