Лекция 1 Числовые системы и коды Числовые

Лекция 1 Числовые системы и коды

Числовые системы и коды Виды числовых систем 1. Непозиционные системы счисления Римская система счисления Греческая система счисления I=(1)10 V=(5)10 X=(10)10 L=(50)10 C=(100)10 D=(500)10 M=(1000)10 1α 100 ρ 2β 20 κ 200 σ 3γ 30 λ 300 τ 4δ 40 μ 400 υ 5ε 50 ν 500 φ 6ς 60 ξ 600 χ 7ζ 70 ο 700 ψ 8η 80 π 800 ω 9θ (1987)10= MCMLXXXVII (31)10 = XXXI (99)10 = XCIX (2009)10 = MMIX 10 ι 90 Ϙ 900 Ϡ (45)10 — με (632)10 — χλβ (970)10 — Ϡο Недостатки непозиционных систем: 1) отсутствие нуля 2) сложность арифметических операций числами 3) ограниченность диапазонов представляемых чисел (3999 и 999 для римской и греческой систем соответственно) 2

Числовые системы и коды Виды числовых систем 2. Позиционные системы счисления Система счисления называется позиционной, если каждому разряду в строке цифр, представляющей произвольное число в этой системе, соответствует определенный вес pn, где p − базис системы, а n − номер позиции разряда Общий способ представления чисел любой позиционной системы счисления Множество {аi} − база или алфавит системы счисления p − основание (базис) системы счисления n − количество целых знаков числа m − количество дробных знаков числа Название системы счисления Двоичная Восьмеричная Десятичная Шестнадцатеричная Основание системы р 2 8 10 16 3 Алфавит системы {аi} {0, 1, 2, 3, 4, 5, 6, 7} {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F}

Числовые системы и коды Виды числовых систем 2. Позиционные системы счисления Представление чисел в двоичной системе счисления Представление чисел в восьмеричной системе счисления Представление чисел в шестнадцатеричной системе счисления Представление чисел в троичной системе счисления 4

Числовые системы и коды Перевод из одной системы счисления в другую Для перевода из одной системы в другую целых чисел можно получить экономное правило, используя представление числа в виде поочередных вложений: Эта формула используется в итеративных алгоритмах преобразования, реализуемых программно. Она служит также основой так называемого метода деления: Перевод из десятичной в двоичную систему: Проверка: 5

Числовые системы и коды Перевод из одной системы счисления в другую Перевод из десятичной в восьмеричную систему: Перевод из десятичной в шестнадцатеричную систему: Существует простой способ перевода из двоичной в восьмеричную и шестнадцатеричную системы благодаря тому, что их основания являются степенями числа 2. Поскольку в строке из 3 битов возможны 8 различных комбинаций, из этого следует, что каждую такую строку можно однозначно представить одной восьмеричной цифрой. Точно так же 4 -битовую строку можно представить одной шестнадцатеричной цифрой: 6

Числовые системы и коды Арифметические операции в различных системах счисления Правила выполнения арифметических операций в различных позиционных системах счисления такие же как и в десятичной системе. При сложении чисел поразрядно складываются сначала единицы, а затем старшие разряды. Если в результате поразрядного сложения получается сумма, большая чем основание той системы счисления, в которой ведётся запись, или равная ему, то выполняется перенос в следующий разряд. 7

Числовые системы и коды Арифметические операции в различных системах счисления Основой для перемножения любых чисел служит таблица умножения, определяющая произведения чисел, меньших, чем основание системы счисления. Ниже приведены таблицы умножения для шестеричной и восьмеричной систем счисления: (*)6 В 0 1 2 3 4 5 0 0 0 0 1 2 3 4 5 А 2 0 2 4 10 12 14 3 0 3 10 13 20 23 4 0 4 12 20 24 32 (*)8 5 0 5 14 23 32 41 B 8 0 1 2 3 4 5 6 7 0 0 0 0 0 1 2 3 4 5 6 7 2 0 2 4 6 10 12 14 16 A 3 4 0 0 3 4 6 10 11 14 14 20 17 24 22 30 25 34 5 0 5 12 17 24 31 36 43 6 0 6 14 22 30 36 44 52 7 0 7 16 25 34 43 52 61

Числовые системы и коды Арифметические операции в различных системах счисления Особенности арифметических операций в двоичной системе счисления Арифметические операции над двоичными числами могут производиться по тем же правилам, что и над десятичными, однако, с целью упрощения цифровых систем для выполнения арифметических операций применяют алгоритмы, отличные от алгоритмов действий десятичной арифметики. В двоичной системе счисления для представления знака числа используется дополнительный знаковый разряд (один или несколько разрядов), который располагается перед старшим числовым разрядом. Для положительных чисел значение знакового разряда знаковый разряд равен 0, для отрицательного числа -- равен 1. Двоичный код со знаком называют также прямым кодом. Обратный код для положительных чисел совпадает с прямым. Для отрицательных чисел производится инвертирование всех разрядов, кроме знакового. 9

Числовые системы и коды Арифметические операции в различных системах счисления Особенности арифметических операций в двоичной системе счисления Арифметические операции над двоичными числами могут производиться по тем же схемам, что и над десятичными. Сводная таблица правил сложения и вычитания в двоичной системе счисления. сin − перенос из предыдущего разряда; сout − перенос в следующий разряд; bin − заём из предыдущего разряда; x, y − значения текущих разрядов; s − значение суммы в текущем разряде; d − значение разницы в текущем разряде; 10

Числовые системы и коды Арифметические операции в различных системах счисления Особенности арифметических операций в двоичной системе счисления Если к обратному коду отрицательного числа добавить единицу, то получится дополнительный код этого числа. Этот код имеет важное свойство: все арифметические операции с числами в этом коде дадут правильный результат. Если получается положительное число, то для проверки правильности операции его преобразовывать не надо, если отрицательное - необходимо перевести в прямой код. Правила перевода в дополнительный код и обратно производятся по одному алгоритму: инвертировать число (исключая знаковый разряд) и добавить к нему 1: 11

Числовые системы и коды Арифметические операции в различных системах счисления Сложение двоичных чисел Правила сложения двух двоичных чисел: Пример сложения многоразрядных чисел. Требуется сложить два числа 1810 и 2310. 12

Числовые системы и коды Арифметические операции в различных системах счисления Вычитание двоичных чисел Вычитание в цифровых системах реализуется с помощью операции сложения. Вычитаемое при этом представляется в дополнительном коде. Рассмотрим два примера, в первом требуется из числа 23 отнять число 18, а во втором из 18 отнять 23. С начала вычитающие представим в дополнительном коде: 13

Числовые системы и коды Арифметические операции в различных системах счисления Умножение двоичных чисел Умножение чисел в двоичной системе производится так же, как и в десятичной, но с учетом правил двоичной арифметики: 14

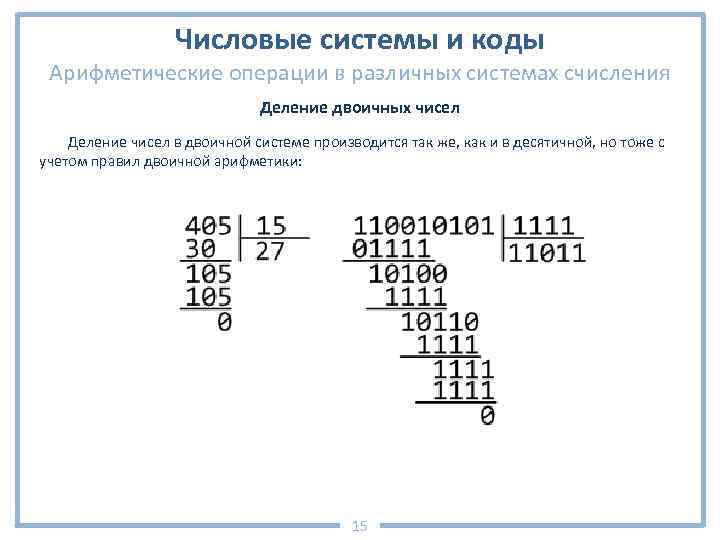Числовые системы и коды Арифметические операции в различных системах счисления Деление двоичных чисел Деление чисел в двоичной системе производится так же, как и в десятичной, но тоже с учетом правил двоичной арифметики: 15