Лекция 1-3 ПМ ВВЕДЕНИЕ В ФИЗИКУ ТВЕРДОГО ТЕЛА.ppt
- Количество слайдов: 67
 Лекция 1 -3 ПМ ВВЕДЕНИЕ В ФИЗИКУ ТВЕРДОГО ТЕЛА 1
Лекция 1 -3 ПМ ВВЕДЕНИЕ В ФИЗИКУ ТВЕРДОГО ТЕЛА 1
 Атомарная структура Размерные эффекты 2
Атомарная структура Размерные эффекты 2
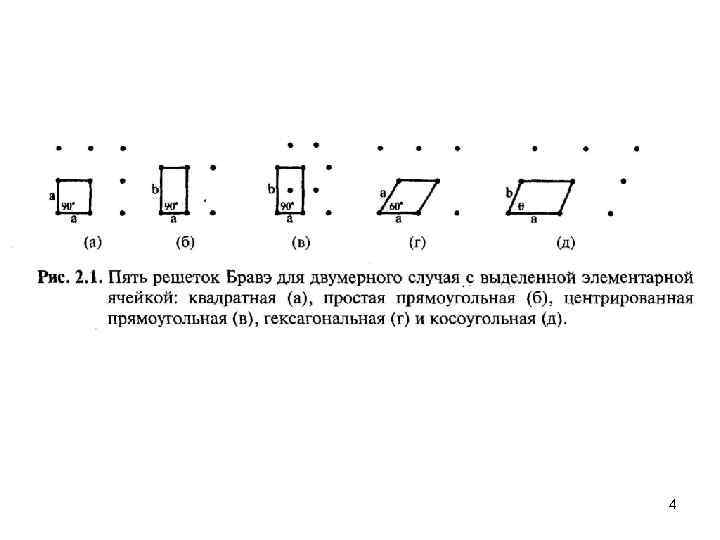
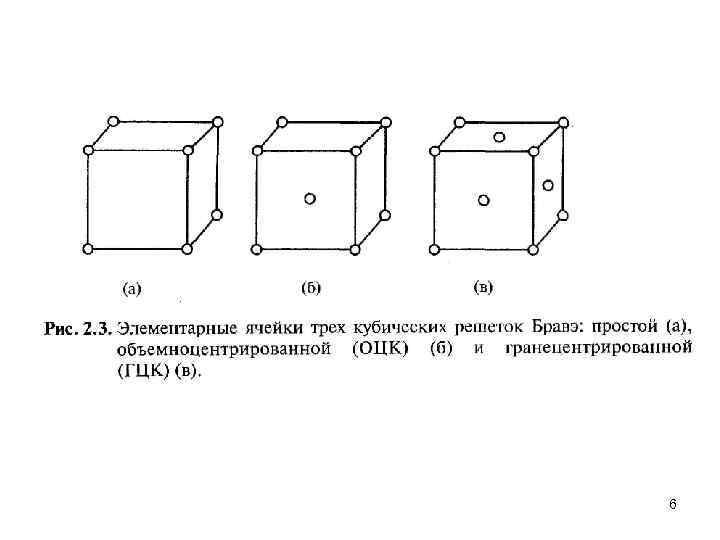
 Кристаллические решетки 3
Кристаллические решетки 3
 4
4
 5
5
 6
6
 7
7
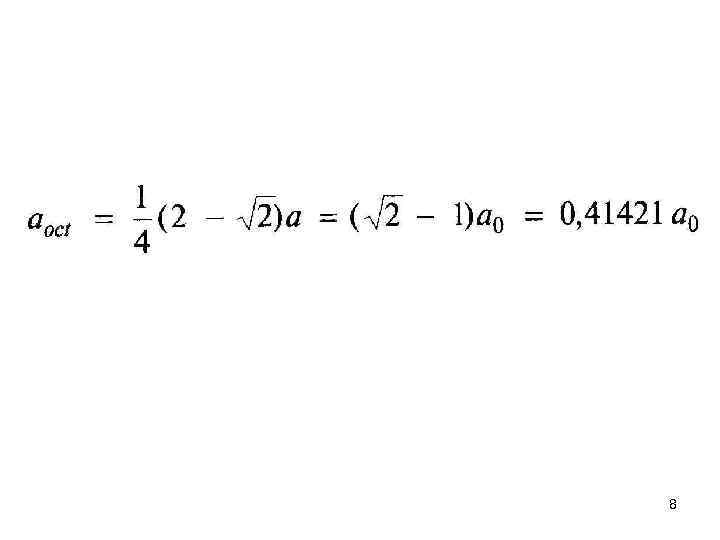 8
8
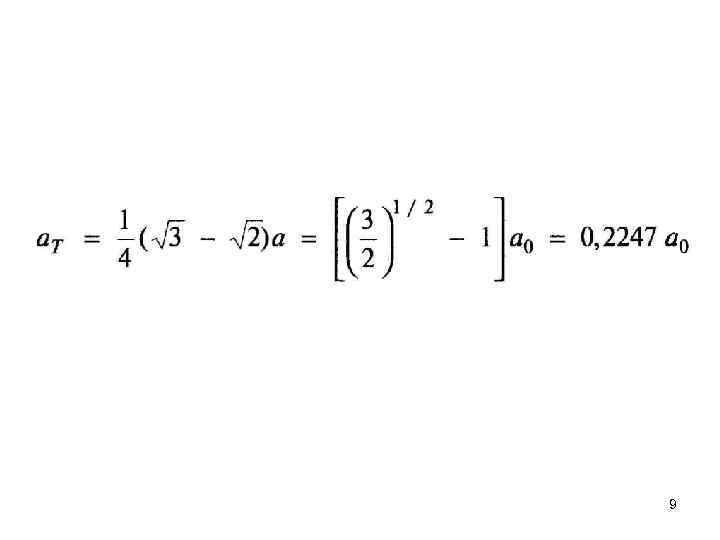 9
9
 Наночастицы с гранецентрированной решеткой 10
Наночастицы с гранецентрированной решеткой 10
 11
11
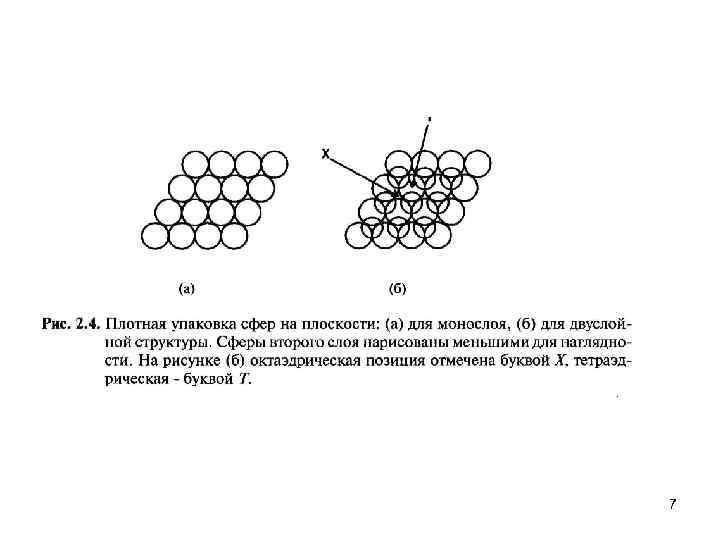
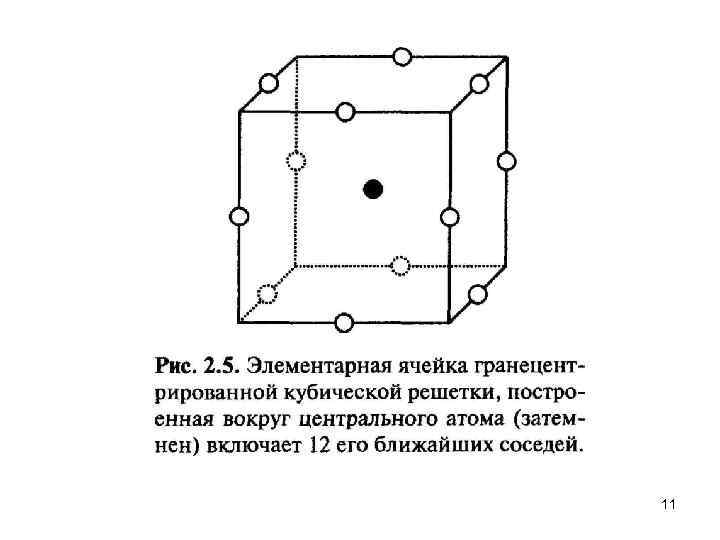
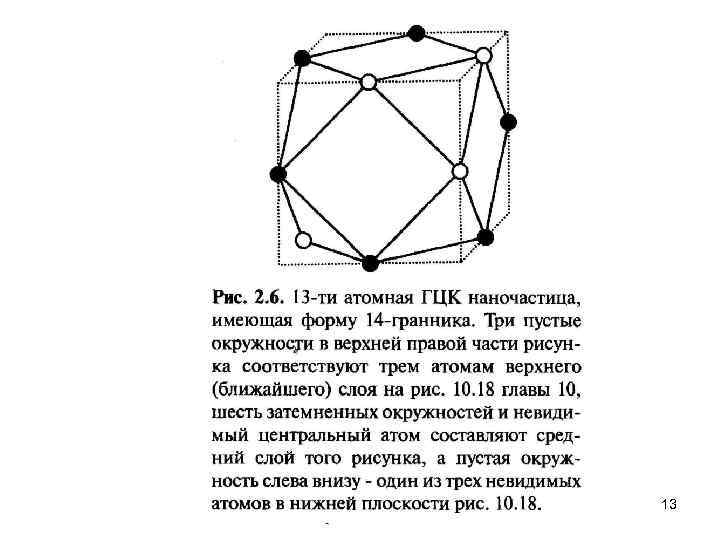
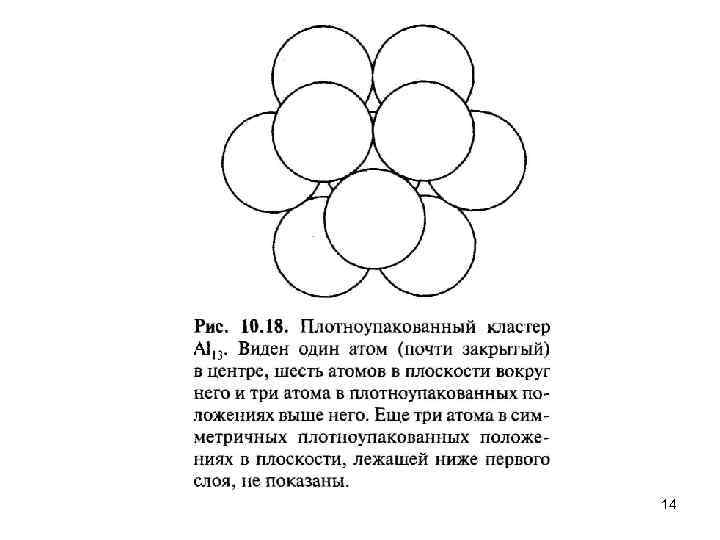
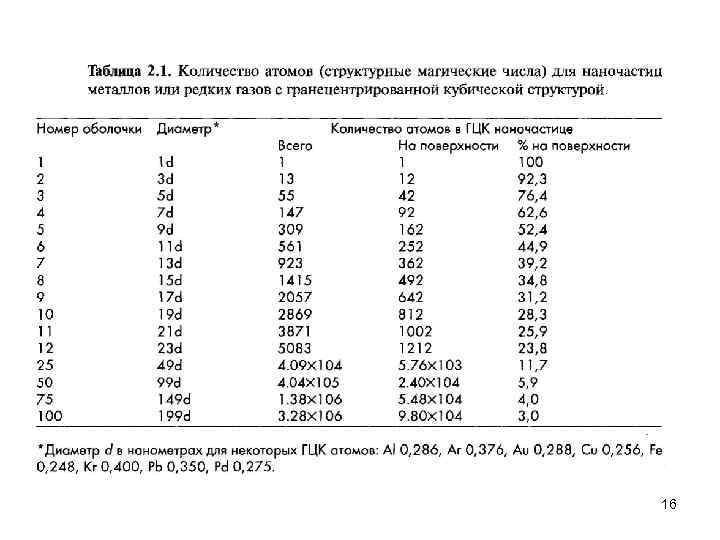
 Большинство металлов кристаллизуются в плотноупакованные решетки. Так, Аg, А 1, Аu, Со, Сu, Рb, Рt и Rh, как и благородные газы Ne, Аr, Кr, Хе, кристаллизуют ся в ГЦК решетку, а Мg, Nd, Оs, Rе, Ru, Y, Zn — в ГПУ. Некоторые другие металлы кристаллизуются в не столь плотно упакованную ОЦК решетку, а такие как Сr, 1 i, Sr могут кристаллизоваться во все три вышеупомянутых типа решеток в зависимости от условий. Каждый атом в обеих плотноупакованных решетках имеет 12 соседей. На рис. 2. 5 показаны 12 соседей атома, находящегося в центре куба (выделен темным цветом) для ГЦК решетки. Такие 13 атомов составляют наименьшую из теоретически возможных наночастиц для ГЦ К решетки. На рис. 2. 6 показан четырнадцатигранник с минимальным объемом, образуемый соединением этих атомов плоскими гранями. Сугано и Коизуми в 1998 году назвали этот многогранник кубоктаэдром. У этого 14 гранника — шесть квадратных граней и 8 граней в форме равностороннего треугольника. Если нарастить на частицу еще один слой, то есть добавить к этим 13 ти атомам еще 42, то получится частица той же декатессараэдрической формы из 55 атомов. Добавляя слои к такой частице, можем получить еще большие наночастицы. Они образуют ряд кластеров с суммарным количеством атомов N= 1, 13, 55, 147, 309, 561, . . . , которые называют структурными магическими числами (Таблица 21). Для п слоев количество атомов N в такой ГЦК наночастице определяется по 12 формуле
Большинство металлов кристаллизуются в плотноупакованные решетки. Так, Аg, А 1, Аu, Со, Сu, Рb, Рt и Rh, как и благородные газы Ne, Аr, Кr, Хе, кристаллизуют ся в ГЦК решетку, а Мg, Nd, Оs, Rе, Ru, Y, Zn — в ГПУ. Некоторые другие металлы кристаллизуются в не столь плотно упакованную ОЦК решетку, а такие как Сr, 1 i, Sr могут кристаллизоваться во все три вышеупомянутых типа решеток в зависимости от условий. Каждый атом в обеих плотноупакованных решетках имеет 12 соседей. На рис. 2. 5 показаны 12 соседей атома, находящегося в центре куба (выделен темным цветом) для ГЦК решетки. Такие 13 атомов составляют наименьшую из теоретически возможных наночастиц для ГЦ К решетки. На рис. 2. 6 показан четырнадцатигранник с минимальным объемом, образуемый соединением этих атомов плоскими гранями. Сугано и Коизуми в 1998 году назвали этот многогранник кубоктаэдром. У этого 14 гранника — шесть квадратных граней и 8 граней в форме равностороннего треугольника. Если нарастить на частицу еще один слой, то есть добавить к этим 13 ти атомам еще 42, то получится частица той же декатессараэдрической формы из 55 атомов. Добавляя слои к такой частице, можем получить еще большие наночастицы. Они образуют ряд кластеров с суммарным количеством атомов N= 1, 13, 55, 147, 309, 561, . . . , которые называют структурными магическими числами (Таблица 21). Для п слоев количество атомов N в такой ГЦК наночастице определяется по 12 формуле
 13
13
 14
14
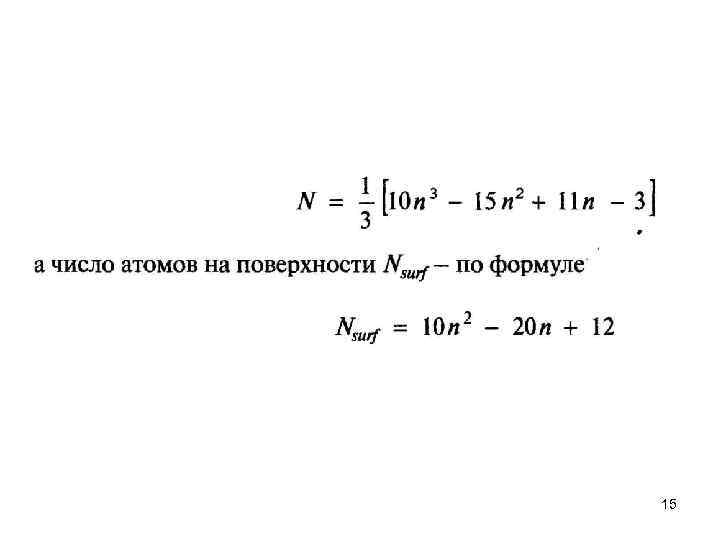 15
15
 16
16
 Если использовать ту же процедуру для построения ГПУ наночастиц, обсуждаемых в предыдущем пара графе, то получим несколько отличный от предыдущего ряд магических чисел, а именно: 1, 13, 57, 153, 321, 581, . . ГЦК — наночастицы из чистых металлов, такие как Аu 55, обычно очень реак ционноспособны и имеют малое время жизни. Их можно стабилизировать лиган дами, добавляя атомные группы между атомами кластера и на его поверхность. Наночастица Аu 55 изучалась в лиганд стабилизированном виде Аu 55(РРh 3)12 С 16 с диаметром ~1, 4 нм, где РРh 3 — органическая группа. В качестве примеров больших кластеров с магическими числами можно привести соединения Р 1309(1. 10 фенантролин)36 О 30 и Рd 561(1, 10 фенантролин)36 О 200 Обсуждаемые магические числа называются структурными из за того, что они получаются при минимизации объема и максимизации плотности наночастицы с формой, близкой к сферической, и плотноупакованной структурой, характерной для объемных тел. Эти магические числа не имеют никакого отношения к электронной структуре составляющих наночастицу атомов. 17
Если использовать ту же процедуру для построения ГПУ наночастиц, обсуждаемых в предыдущем пара графе, то получим несколько отличный от предыдущего ряд магических чисел, а именно: 1, 13, 57, 153, 321, 581, . . ГЦК — наночастицы из чистых металлов, такие как Аu 55, обычно очень реак ционноспособны и имеют малое время жизни. Их можно стабилизировать лиган дами, добавляя атомные группы между атомами кластера и на его поверхность. Наночастица Аu 55 изучалась в лиганд стабилизированном виде Аu 55(РРh 3)12 С 16 с диаметром ~1, 4 нм, где РРh 3 — органическая группа. В качестве примеров больших кластеров с магическими числами можно привести соединения Р 1309(1. 10 фенантролин)36 О 30 и Рd 561(1, 10 фенантролин)36 О 200 Обсуждаемые магические числа называются структурными из за того, что они получаются при минимизации объема и максимизации плотности наночастицы с формой, близкой к сферической, и плотноупакованной структурой, характерной для объемных тел. Эти магические числа не имеют никакого отношения к электронной структуре составляющих наночастицу атомов. 17
 Иногда фактором, определяющим энергетический минимум структуры малой наночастицы, является взаимодействие валентных электронов, составляющих частицу атомов с усредненным молекулярным потенциалом, так что электроны находятся на орбитальных уровнях, определяемых именно этим потенциалом. Конфигурации атомных кластеров, в которых такие электроны образуют заполненные оболочки, особенно устойчивы порождают электронные магические числа. Когда были получены массовые спектры наночастиц натрия Nа. N в массовом распределении были обнаружены пики, соответствующие первым 15 ти электронным магическим числам N = 3, 9, 20, 36, 61, . . . вплоть до N = 1220 при п = 15 и ГЦК структурные магические числа для больших кластеров, начиная с N= 1415 для п = 8. На рис. 2. 7 даны масс спектрометрические данные в зависимости от кубического корня из числа атомов N 1/3. Видно, что линии обоих наборов магических чисел равноудалены друг от друга, с расстоянием между структурными магическими числами примерно в 2. 6 раза большим, чем между электронными. Этот рисунок свидетельствует в пользу того, что меньшие кластеры определяются электронной структурой, а большие — структурой кристаллической решетки. 18
Иногда фактором, определяющим энергетический минимум структуры малой наночастицы, является взаимодействие валентных электронов, составляющих частицу атомов с усредненным молекулярным потенциалом, так что электроны находятся на орбитальных уровнях, определяемых именно этим потенциалом. Конфигурации атомных кластеров, в которых такие электроны образуют заполненные оболочки, особенно устойчивы порождают электронные магические числа. Когда были получены массовые спектры наночастиц натрия Nа. N в массовом распределении были обнаружены пики, соответствующие первым 15 ти электронным магическим числам N = 3, 9, 20, 36, 61, . . . вплоть до N = 1220 при п = 15 и ГЦК структурные магические числа для больших кластеров, начиная с N= 1415 для п = 8. На рис. 2. 7 даны масс спектрометрические данные в зависимости от кубического корня из числа атомов N 1/3. Видно, что линии обоих наборов магических чисел равноудалены друг от друга, с расстоянием между структурными магическими числами примерно в 2. 6 раза большим, чем между электронными. Этот рисунок свидетельствует в пользу того, что меньшие кластеры определяются электронной структурой, а большие — структурой кристаллической решетки. 18
 19
19
 Тетраэдрические полупроводниковые структуры 20
Тетраэдрические полупроводниковые структуры 20
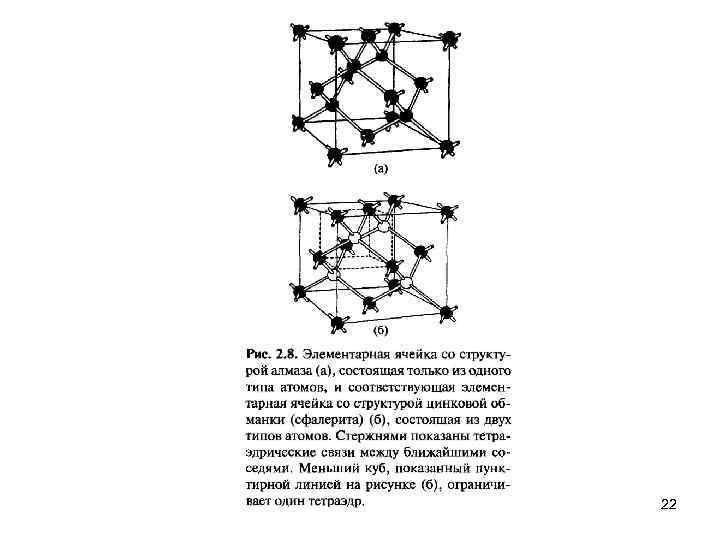
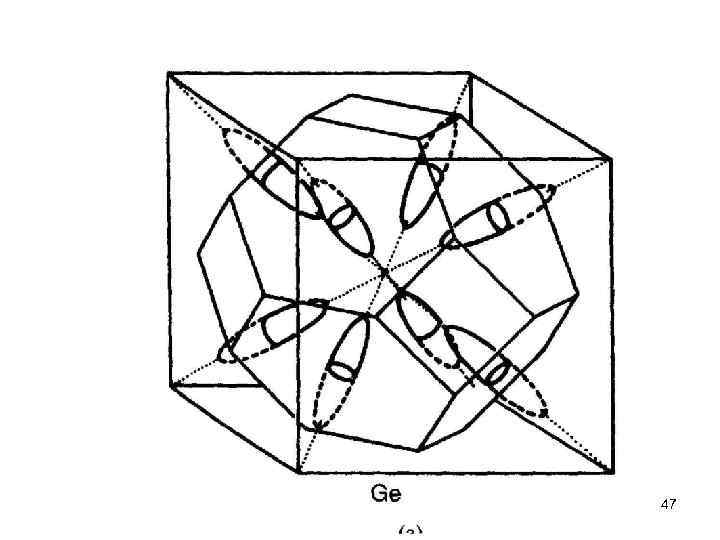
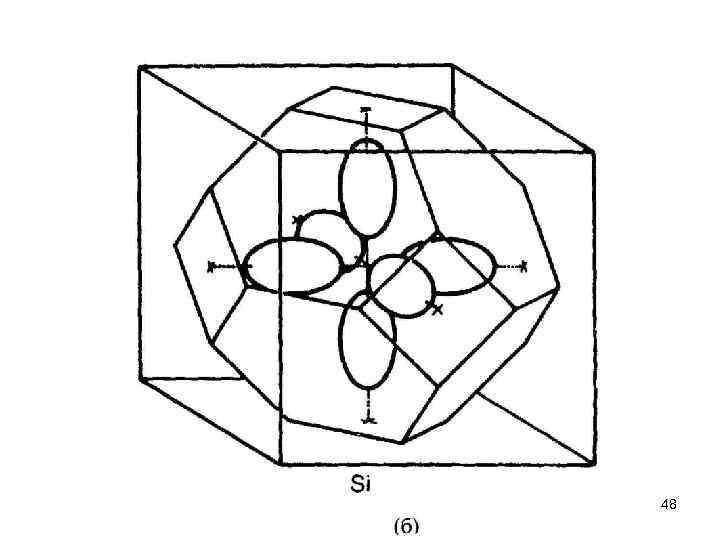
 В полупроводниковых соединениях типа АIIIВV и АIIВV 1, таких как Gа. Аs и Sn. S соответственно, атомы одного типа кристаллизуются в ГЦК подрешетку в позициях [000], [О 1/21/2], [1/2 О 1/2] и [1/21/20], а атомы второго типа — в аналогичную ГЦК подрешетку, сдвинутую относительно первой на [1/41/41/4] по диагонали куба, как показано на рис. 2. 8 b. Такая решетка называется сфалеритом, цинковой обманкой или решеткой типа Zn. S. На рисунке видно, что каждый атом цинка (светлый кружок) находится в центре тетраэдра из атомов серы (темные кружки) и наоборот, каждый атом серы имеет в качестве ближайших соседей четыре атома цинка. Кремний и германий кристаллизуются в такую же решетку, причем атомы этих веществ занимают узлы обеих подрешеток, так что в элементарной ячейке оказываются восемь одинаковых атомов. Такое расположение атомов, показанное на рис. 2. 8 а, называется алмазной решеткой. И кремний, и германий имеют валентность, равную четырем, так что с точки зрения образования химических связей, четыре соседа в вершинах правильного тетраэдра является оптимальной конфигурацией. 21
В полупроводниковых соединениях типа АIIIВV и АIIВV 1, таких как Gа. Аs и Sn. S соответственно, атомы одного типа кристаллизуются в ГЦК подрешетку в позициях [000], [О 1/21/2], [1/2 О 1/2] и [1/21/20], а атомы второго типа — в аналогичную ГЦК подрешетку, сдвинутую относительно первой на [1/41/41/4] по диагонали куба, как показано на рис. 2. 8 b. Такая решетка называется сфалеритом, цинковой обманкой или решеткой типа Zn. S. На рисунке видно, что каждый атом цинка (светлый кружок) находится в центре тетраэдра из атомов серы (темные кружки) и наоборот, каждый атом серы имеет в качестве ближайших соседей четыре атома цинка. Кремний и германий кристаллизуются в такую же решетку, причем атомы этих веществ занимают узлы обеих подрешеток, так что в элементарной ячейке оказываются восемь одинаковых атомов. Такое расположение атомов, показанное на рис. 2. 8 а, называется алмазной решеткой. И кремний, и германий имеют валентность, равную четырем, так что с точки зрения образования химических связей, четыре соседа в вершинах правильного тетраэдра является оптимальной конфигурацией. 21
 22
22
 23
23
 Ионная модель хорошо описывает данные для щелочно галлоидных и ще лочноземельно халькогенидных соединений. Однако ни одна из упомянутых вы ше моделей не дает удовлетворительного соответствия для полупроводниковых соединений. Вопрос о том, в какой степени связи в полупроводниковых кристал лах являются ионными, а в какой ковалентными, не может быть решен на осно вании кристаллографических данных. Если волновую функцию, описывающую связь, записать в виде 24
Ионная модель хорошо описывает данные для щелочно галлоидных и ще лочноземельно халькогенидных соединений. Однако ни одна из упомянутых вы ше моделей не дает удовлетворительного соответствия для полупроводниковых соединений. Вопрос о том, в какой степени связи в полупроводниковых кристал лах являются ионными, а в какой ковалентными, не может быть решен на осно вании кристаллографических данных. Если волновую функцию, описывающую связь, записать в виде 24
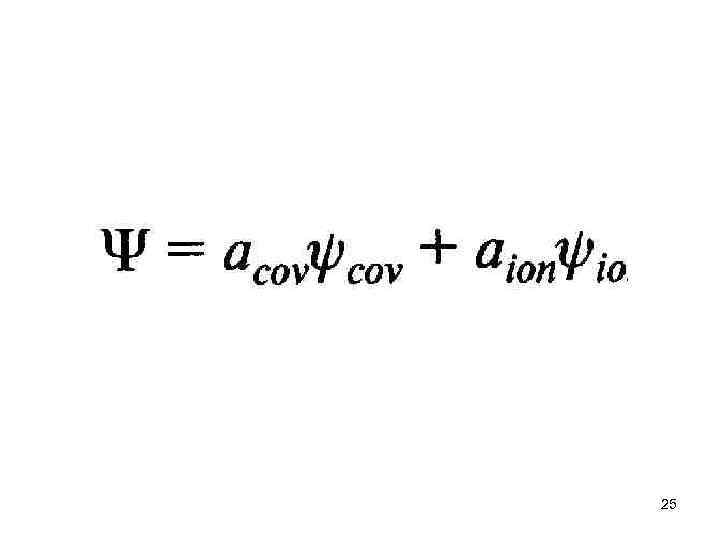 25
25
 а 2 cov определяет ковалентную, а а 2 iоп ионную долю в такой смешанной связи 26
а 2 cov определяет ковалентную, а а 2 iоп ионную долю в такой смешанной связи 26
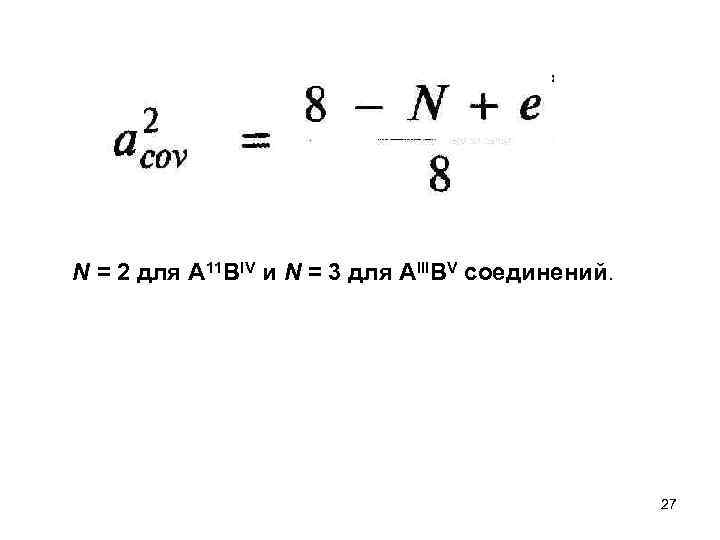 N = 2 для А 11 BIV и N = 3 для АIIIВV соединений. 27
N = 2 для А 11 BIV и N = 3 для АIIIВV соединений. 27
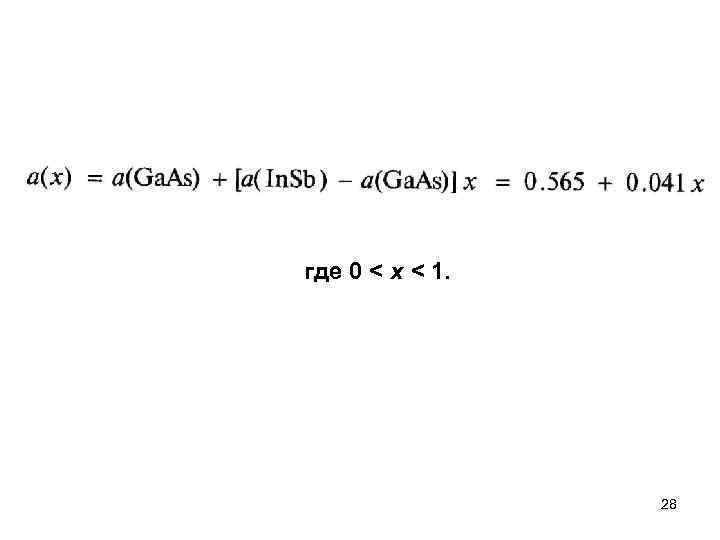 где 0 < х < 1. 28
где 0 < х < 1. 28
 Колебания решетки 29
Колебания решетки 29
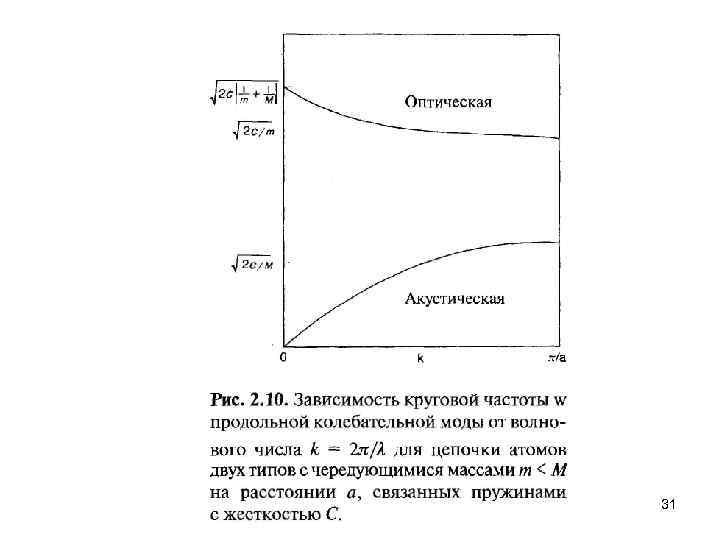
 ~т~М~т~М~ Когда одна из пружин сжата или растянута на величину х, на соседние массы действует сила величиной С х, где С — жесткость пружины. Так как пружины растягиваются и сжимаются последовательно друг с другом, имеет место продольная колебательная мода, в которой атомы движутся вдоль направления пружин. Каждая нормальная мода характеризуется своей частотой , волновым числом k: = 2 / , где — длина волны, и энергией Е, связанной с ней посредством Е = h. Существуют и поперечные нормальные моды, в которых атомы колеблются перпендикулярно линии их связей. На рис. 2. 10 показана зависимость от k для низочастотных акустических и высоко частотныхоптических продольных мод. 30
~т~М~т~М~ Когда одна из пружин сжата или растянута на величину х, на соседние массы действует сила величиной С х, где С — жесткость пружины. Так как пружины растягиваются и сжимаются последовательно друг с другом, имеет место продольная колебательная мода, в которой атомы движутся вдоль направления пружин. Каждая нормальная мода характеризуется своей частотой , волновым числом k: = 2 / , где — длина волны, и энергией Е, связанной с ней посредством Е = h. Существуют и поперечные нормальные моды, в которых атомы колеблются перпендикулярно линии их связей. На рис. 2. 10 показана зависимость от k для низочастотных акустических и высоко частотныхоптических продольных мод. 30
 31
31
 Видно, что частота акустической ветви монотонно увеличивается с увеличением волнового числа, а оптической монотонно падает. Эти две ветви имеют предельные частоты (2 С/M)1/2 и (2 С/m)1/2 с энергетической щелью между ними на границе зоны Бриллюэна kтах = /а, где а — равновесное расстояние между атомами М и m. Зона Бриллюэна — это элементарная ячейка в пространстве волновых чисел, или обратном пространстве, что будет излагаться далее в этой главе. Оптическая колебательная ветвь находится в инфракрасном диапазоне, обычно на частотах от 1012 до Зх1014 Гц. Характерные частоты акустической ветви много ниже. В трехмерном случае ситуация более сложна, и следует рассматривать продольную акустическую, продольную оптическую, поперечную акустическую и поперечную оптическую ветви. 32
Видно, что частота акустической ветви монотонно увеличивается с увеличением волнового числа, а оптической монотонно падает. Эти две ветви имеют предельные частоты (2 С/M)1/2 и (2 С/m)1/2 с энергетической щелью между ними на границе зоны Бриллюэна kтах = /а, где а — равновесное расстояние между атомами М и m. Зона Бриллюэна — это элементарная ячейка в пространстве волновых чисел, или обратном пространстве, что будет излагаться далее в этой главе. Оптическая колебательная ветвь находится в инфракрасном диапазоне, обычно на частотах от 1012 до Зх1014 Гц. Характерные частоты акустической ветви много ниже. В трехмерном случае ситуация более сложна, и следует рассматривать продольную акустическую, продольную оптическую, поперечную акустическую и поперечную оптическую ветви. 32
 Обсуждаемые колебания атомов относятся к типу стоячих волн. Бывают и бегущие волны, когда локализованная область колеблющихся атомов перемещается по кристаллу. Примерами таких бегущих волн являются звук, распространяю щийсяв воздухе или сейсмические колебания почвы, расходящиеся от эпицентра землетрясения на тысячи километров и позволяющие сейсмографам зарегистрировать землетрясение спустя многие минуты. Локализованные бегущие волны колебаний атомов в кристалле называются фононами. Их энергия квантуется как Е= = h , где = /2 — частота колебаний в такой волне. Фононы играют важную роль в физике твердого тела. 33
Обсуждаемые колебания атомов относятся к типу стоячих волн. Бывают и бегущие волны, когда локализованная область колеблющихся атомов перемещается по кристаллу. Примерами таких бегущих волн являются звук, распространяю щийсяв воздухе или сейсмические колебания почвы, расходящиеся от эпицентра землетрясения на тысячи километров и позволяющие сейсмографам зарегистрировать землетрясение спустя многие минуты. Локализованные бегущие волны колебаний атомов в кристалле называются фононами. Их энергия квантуется как Е= = h , где = /2 — частота колебаний в такой волне. Фононы играют важную роль в физике твердого тела. 33
 Структуры энергетических зон Диэлектрики, полупроводники и проводники 34
Структуры энергетических зон Диэлектрики, полупроводники и проводники 34
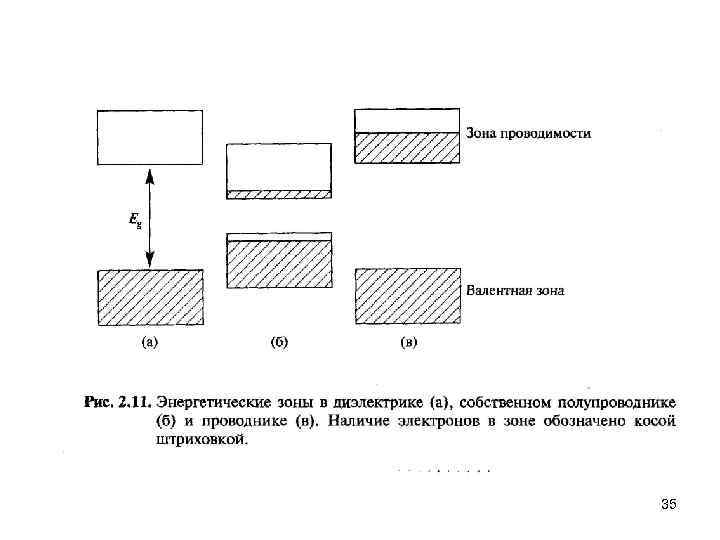 35
35
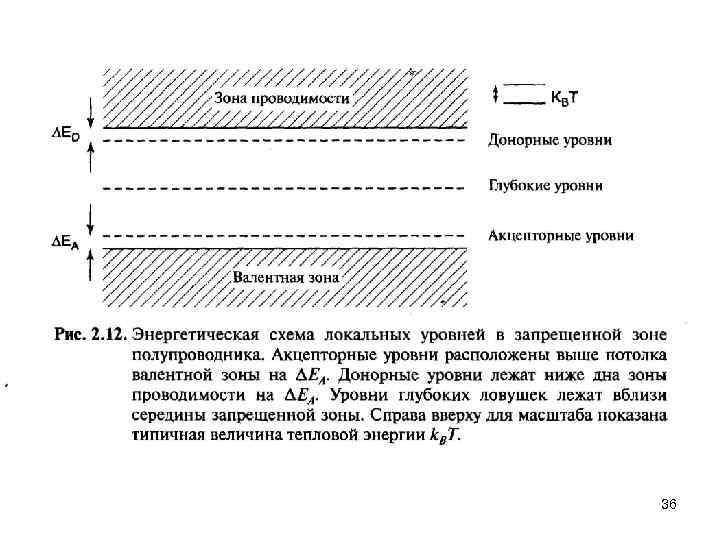 36
36
 Обратное пространство и решетка 37
Обратное пространство и решетка 37
 38
38
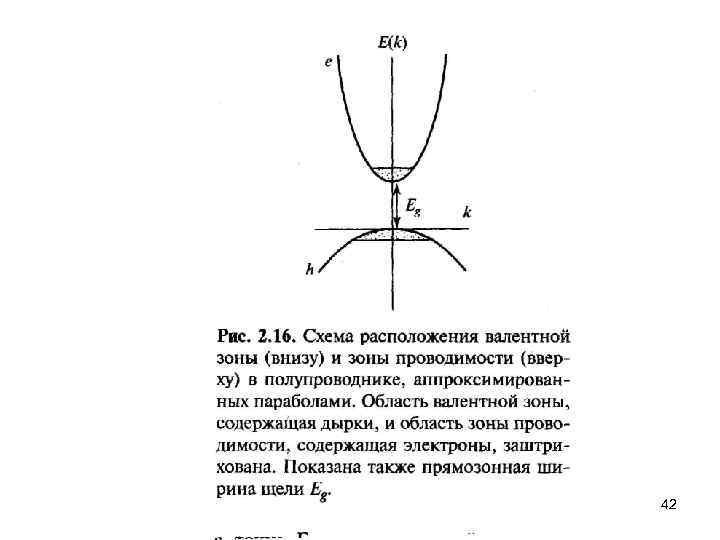
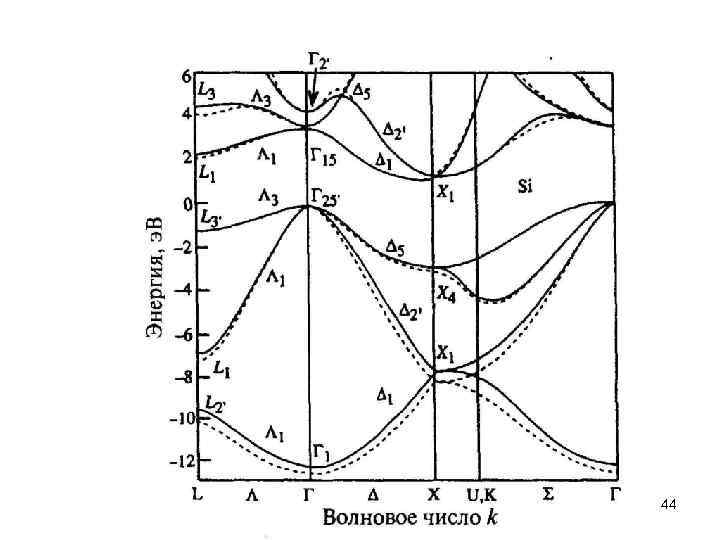
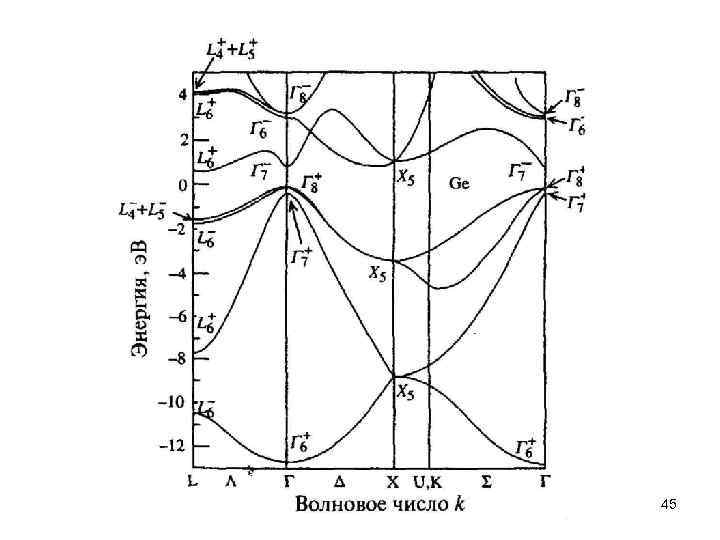
 Энергетические зоны и щели в полупроводниках 39
Энергетические зоны и щели в полупроводниках 39
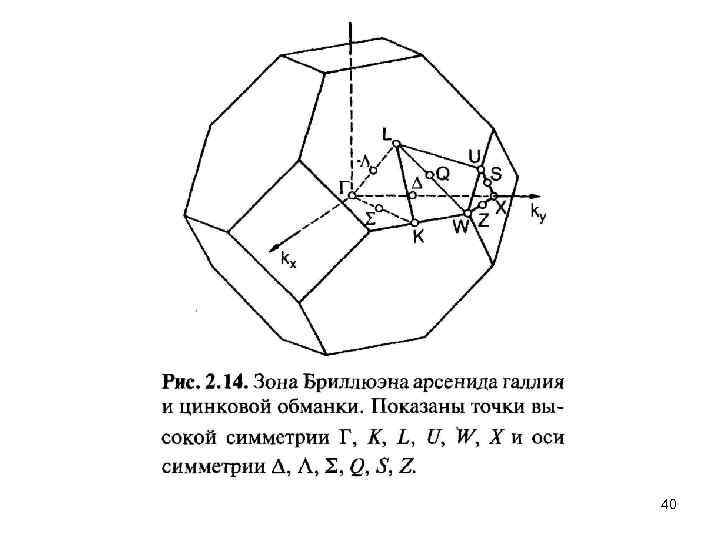 40
40
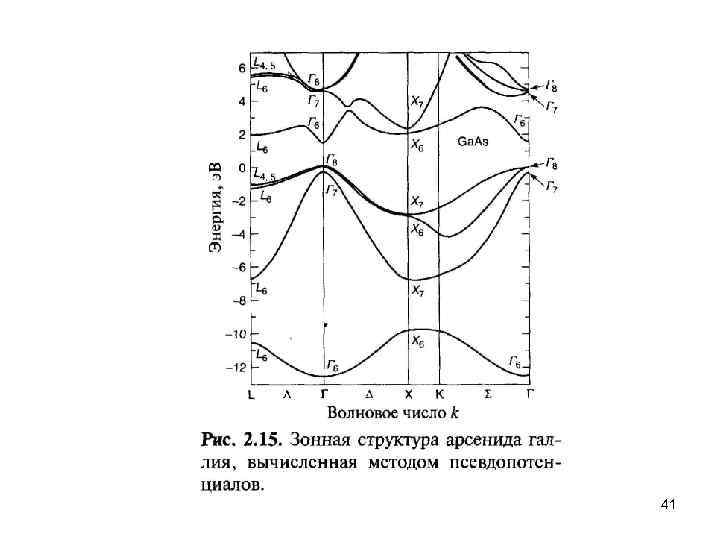 41
41
 42
42
 43
43
 44
44
 45
45
 46
46
 47
47
 48
48
 49
49
 Эффективные массы 50
Эффективные массы 50
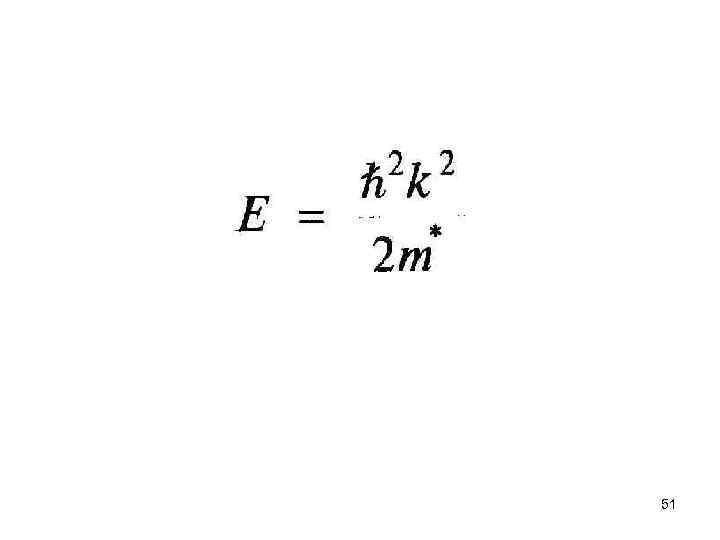 51
51
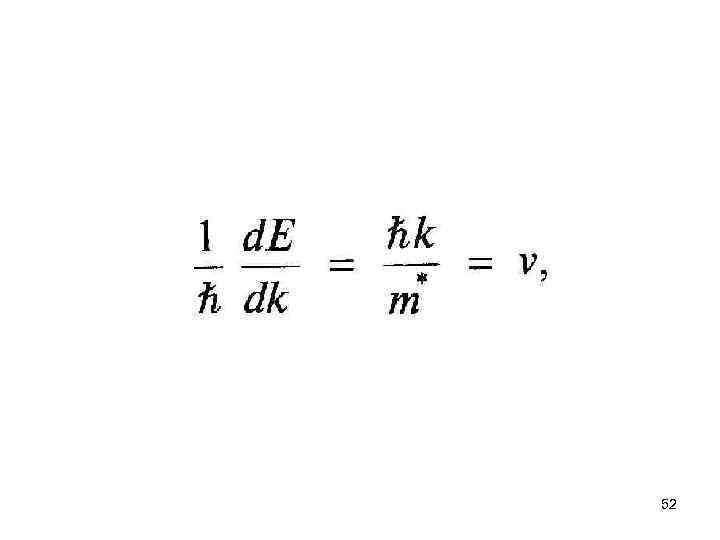 52
52
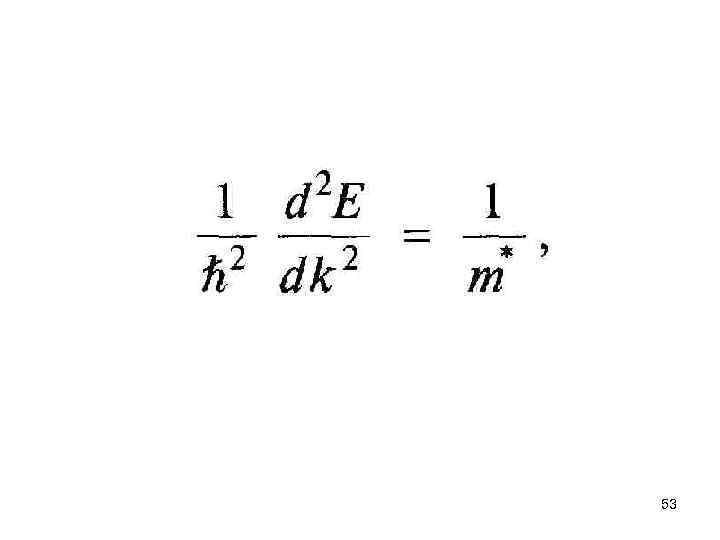 53
53
 Поверхности Ферми 54
Поверхности Ферми 54
 где Етах — максимальная энергия электронов и их масса т*, нормированная на массу свободного электрона те. 55
где Етах — максимальная энергия электронов и их масса т*, нормированная на массу свободного электрона те. 55
 56
56
 Локализованные частицы и квазичастицы Доноры, акцепторы и глубоколежащие уровни Подвижность 57
Локализованные частицы и квазичастицы Доноры, акцепторы и глубоколежащие уровни Подвижность 57
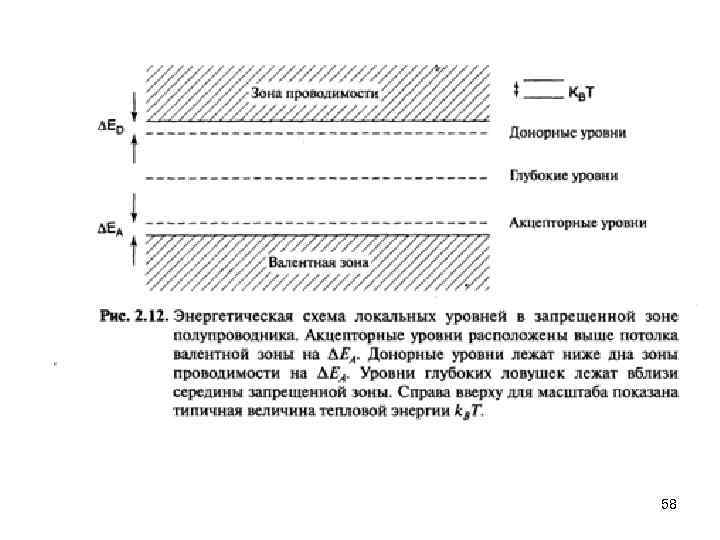 58
58
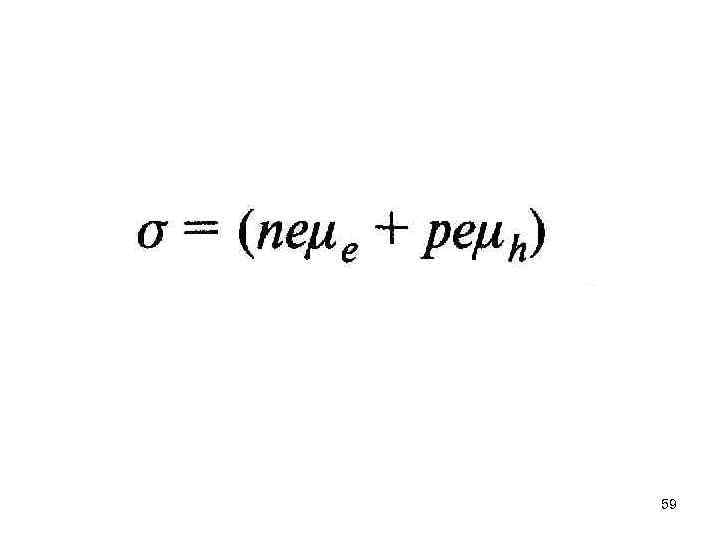 59
59
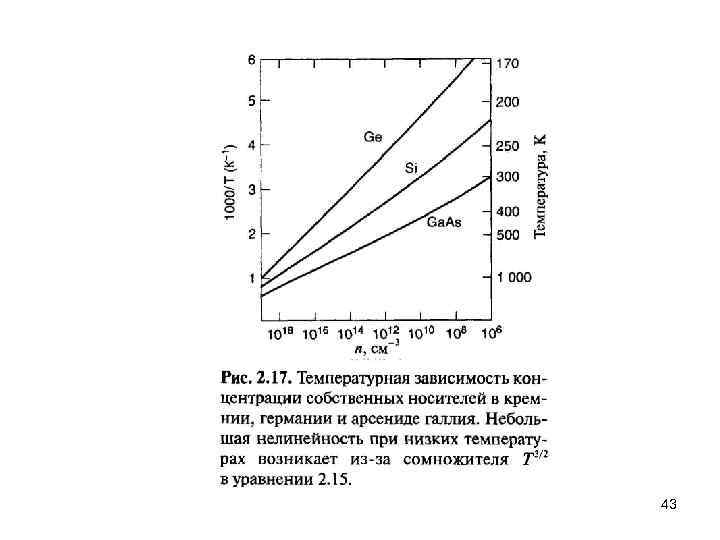
 где собственные концентрации электронов пi и дырок рi равны другу из-за того, что тепловое возбуждение пi электронов в зону проводимости оставляет такое же количество pi, дырок в валентной зоне, т. е. пi = pi. 60
где собственные концентрации электронов пi и дырок рi равны другу из-за того, что тепловое возбуждение пi электронов в зону проводимости оставляет такое же количество pi, дырок в валентной зоне, т. е. пi = pi. 60
 Экситоны 61
Экситоны 61
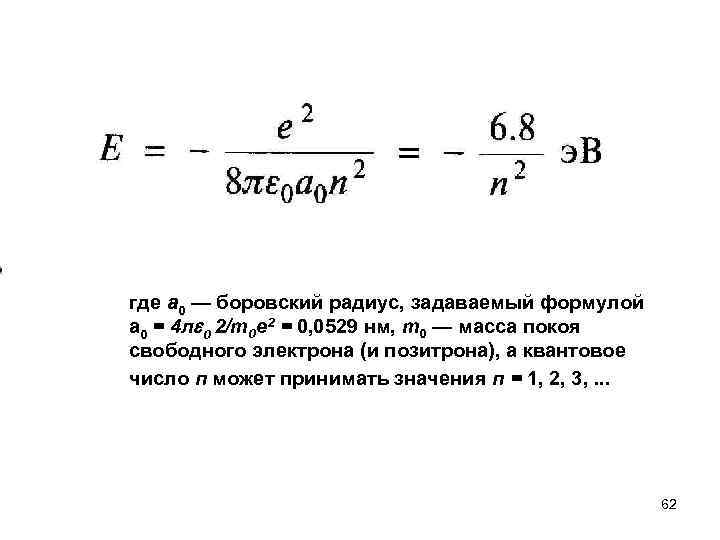 где a 0 — боровский радиус, задаваемый формулой a 0 = 4 л 0 2/т0 е 2 = 0, 0529 нм, m 0 — масса покоя свободного электрона (и позитрона), а квантовое число п может принимать значения п = 1, 2, 3, . . . 62
где a 0 — боровский радиус, задаваемый формулой a 0 = 4 л 0 2/т0 е 2 = 0, 0529 нм, m 0 — масса покоя свободного электрона (и позитрона), а квантовое число п может принимать значения п = 1, 2, 3, . . . 62
 63
63
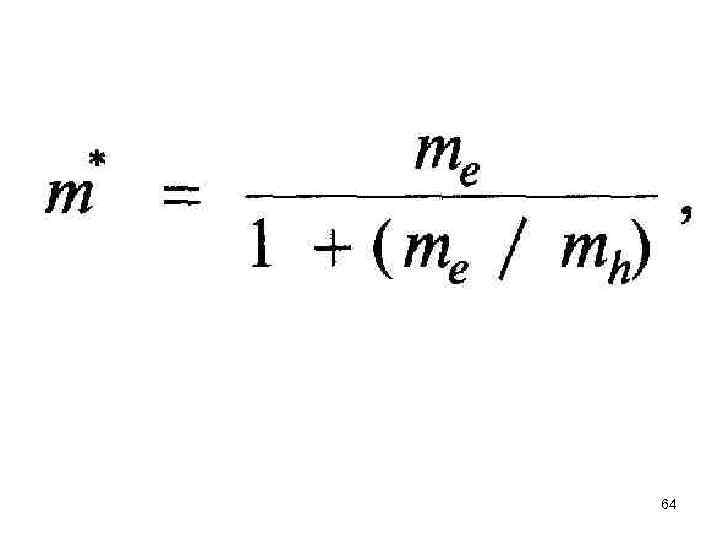 64
64
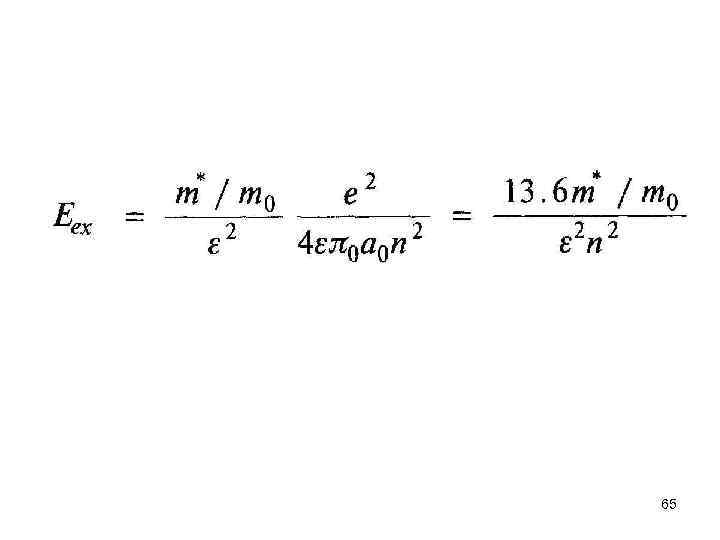 65
65
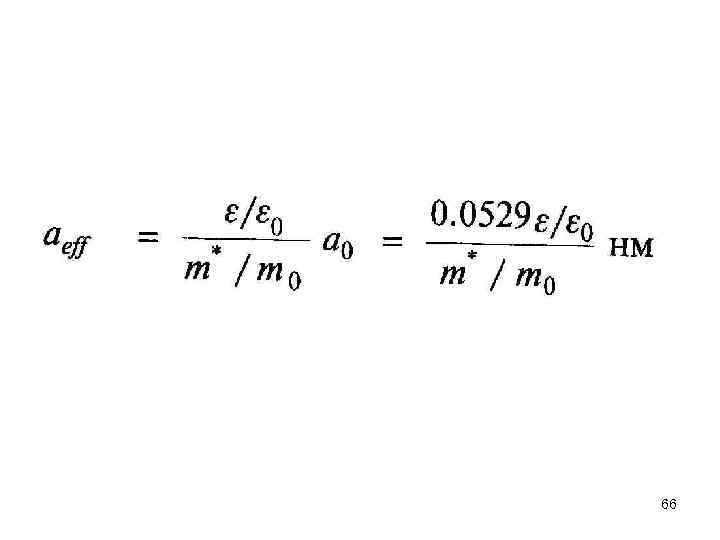 66
66
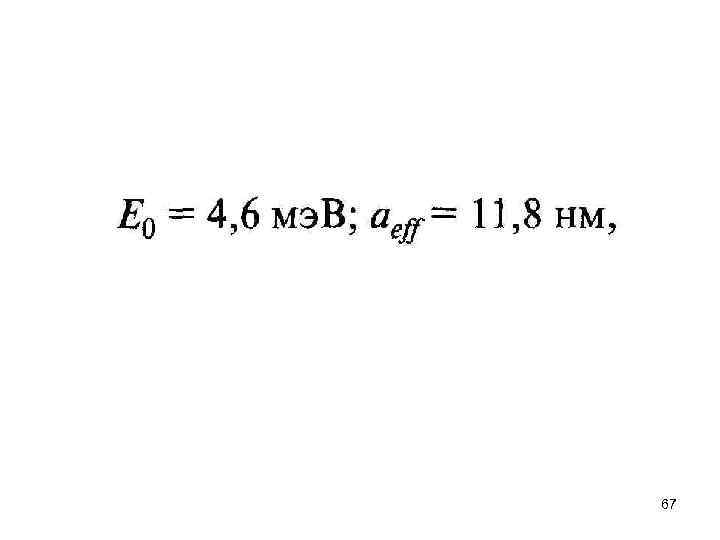 67
67


